- Последние действия на сайте
- Интегральное уравнение
- Материал из Википедии — свободной энциклопедии
- Классификация интегральных уравнений
- Линейные интегральные уравнения
- Уравнения Фредгольма
- Уравнения Вольтерра
- Нелинейные уравнения
- Уравнения Урысона
- Уравнения Гаммерштейна
- Уравнения Ляпунова — Лихтенштейна
- Нелинейное уравнение Вольтерра
- Методы решения
- Преобразование Лапласа
- Метод последовательных приближений
- Метод резольвент
- Метод сведения к алгебраическому уравнению
- Приложения
- Формула обращения Фурье
- Сведение задачи Коши к интегральному уравнению
- Задача Абеля
- 📹 Видео
Последние действия на сайте
Интегральное уравнение
Материал из Википедии — свободной энциклопедии
Интегра́льное уравне́ние — функциональное уравнение, содержащее интегральное преобразование над неизвестной функцией. Если интегральное уравнение содержит также производные от неизвестной функции, то говорят об интегро-дифференциальном уравнении.
Видео:Метод итераций (последовательных приближений)Скачать

Классификация интегральных уравнений
Линейные интегральные уравнения
Это интегральные уравнения, в которые неизвестная функция входит линейно:
где 


Уравнения Фредгольма
Уравнения Фредгольма 2-го рода
Уравнения Фредгольма 2-го рода — это уравнения вида:
Пределы интегрирования могут быть как конечными, так и бесконечными. Переменные удовлетворяют неравенству: 

Ядра, удовлетворяющие последнему условию, называют фредгольмовыми. Если 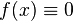
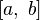
Уравнения Фредгольма 1-го рода
Уравнения Фредгольма 1-го рода выглядят также, как и уравнение Фредгольма 2-го рода, только в них отсутствует часть, содержащая неизвестную функцию вне интеграла:
при этом ядро и свободный член удовлетворяют условиям, сформулированным для уравнений Фредгольма 2-го рода.
Уравнения Вольтерра
Уравнения Вольтерра 2-го рода
Уравнения Вольтерра отличаются от уравнений Фредгольма тем, что один из пределов интегрирования в них является переменным:
Уравнения Вольтерра 1-го рода
Также, как и для уравнений Фредгольма, в уравнениях Вольтерра 1-го рода отсутствует неизвестная функция вне интеграла:
В принципе, уравнения Вольтерра можно рассматривать как частный случай уравнений Фредгольма, если переопределить ядро:
Однако некоторые свойства уравнений Вольтерра не могут быть применены к уравнениям Фредгольма.
Нелинейные уравнения
Можно придумать немыслимое многообразие нелинейных уравнений, поэтому дать им полную классификацию не представляется возможным. Вот лишь их некоторые типы, имеющие большое теоретическое и прикладное значение.
Уравнения Урысона
Постоянная M — это некоторое положительное число, которое заранее не всегда может быть определено.
Уравнения Гаммерштейна
Уравнения Гаммерштейна являются важным частным случаем уравнения Урысона:
где 
Уравнения Ляпунова — Лихтенштейна
Именами Ляпунова — Лихтенштейна принято называть уравнения, содержащие существенно нелинейные операторы, например, уравнение вида:
Нелинейное уравнение Вольтерра
где функция 
Видео:5. Метод последовательных приближенийСкачать
Методы решения
Прежде, чем рассмотреть некоторые методы решения интегральных уравнений, следует заметить, что для них, как и для дифференциальных уравнений не всегда удается получить точное аналитическое решение. Выбор метода решения зависит от вида уравнения. Здесь будут рассмотрены несколько методов для решения линейных интегральных уравнений.
Преобразование Лапласа
Метод преобразования Лапласа может быть применён к интегральному уравнению, если входящий в него интеграл имеет вид свёртки двух функций:
то есть, когда ядро является функцией разности двух переменных:
Например, дано такое уравнение:
Применим преобразование Лапласа к обеим частям уравнения:

Применяя обратное преобразование Лапласа, получим:
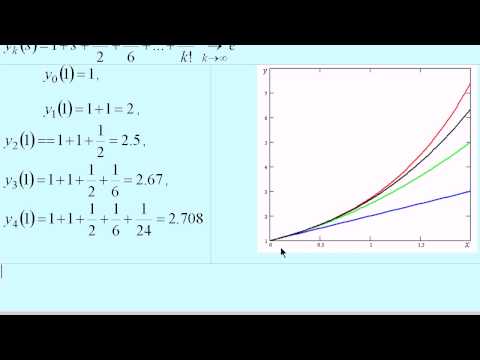
Метод последовательных приближений
Метод последовательных приближений применяется для уравнений Фредгольма 2-го рода, если выполняется условие:
Это условие необходимо для сходимости ряда Лиувилля — Неймана:
который и является решением уравнения. (K k f)(x) — k -ая степень интегрального оператора (Kf)(x) :
Впрочем, такое решение является хорошим приближением лишь при достаточно малых | λ | .
Метод резольвент
Метод резольвент является не самым быстрым решением интегрального уравнения Фредгольма второго рода, однако иногда нельзя указать других путей решения задачи.
Если ввести следующие обозначения:
то повторными ядрами ядра 
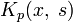
Ряд, составленный из повторных ядер,
называется резольвентой ядра 


Например, для интегрального уравнения
повторными будут следующие ядра:
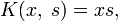
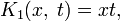

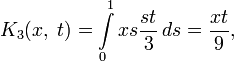
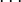
а резольвентой — функция
Тогда решение уравнения находится по формуле:
Метод сведения к алгебраическому уравнению
В случае, если ядро интегрального уравнения Фредгольма является вырожденным, то есть 
где 
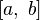
где 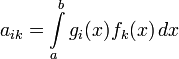

Видео:Интегральные уравнения Вольтерра второго рода Метод последовательных приближенийСкачать

Приложения
Термин «интегральное уравнение» ввёл в 1888 году Дюбуа-Реймон, однако первые задачи с интегральными уравнениями решались и ранее. Например, в 1811 году Фурье решил задачу об обращении интеграла, которая теперь носит его имя.
Формула обращения Фурье
Задача состоит в нахождении неизвестной функции f(y) по известной функции g(x) :
Фурье получил выражение для функции f(y) :
Сведение задачи Коши к интегральному уравнению
К нелинейным интегральным уравнениям Вольтерра приводит задача Коши для обыкновенных дифференциальных уравнений:
В самом деле, это уравнение можно проинтегрировать по t от a до t :
Решение начальной задачи для линейных дифференциальных уравнений приводит к линейным интегральным уравнениям Вольтерра 2-го рода. Этим еще в 1837 году воспользовался Лиувилль. Пусть, например, поставлена задача:
Для уравнения с постоянными коэффициентами с теми же начальными условиями:
решение может быть найдено методом вариации постоянных и представлено в виде:
Тогда для исходного уравнения получается:
— интегральное уравнение Вольтерра 2-го рода.
a,» src=»http://upload.wikimedia.org/math/3/c/c/3cca9038417f8968682c783191e3f6c7.png» />
также может быть сведено к интегральному уравнению Вольтерра 2-го рода.
Задача Абеля
Исторически считается, что первой задачей, которая привела к необходимости рассмотрения интегральных уравнений, является задача Абеля. В 1823 году Абель, занимаясь обобщением задачи о таутохроне, пришёл к уравнению:
где f(x) — заданная функция, а 
У Абеля формулировка задачи выглядела примерно так:
Материальная точка под действием силы тяжести движется в вертикальной плоскости
по некоторой кривой. Требуется определить эту кривую так, чтобы материальная точка, начав свое движение без начальной скорости в точке кривой с ординатой x , достигла оси Oξ за время t = f1(x) , где f1(x) — заданная функция.
Если обозначить угол между касательной к траектории и осью Oξ как β и применить законы Ньютона, можно прийти к следующему уравнению:
📹 Видео
Уравнения Фредгольма - 1Скачать

Методы численного анализа - Уравнения Фредгольма и ВольтерраСкачать

Метод последовательного приближения или от простого к сложномуСкачать

Метод Пикара последовательных приближений для решения дифференциальных уравненийСкачать

Решаем диффуры методом последовательных приближенийСкачать

Курс по ИДУ: Методы решения интегральных уравнений Вольтерра и Фредгольма | Занятие 6Скачать

Уравнения Вольтерра - 2Скачать

Острые диффуры, или как научиться решать методом последовательных приближенийСкачать

Интегральные уравнения ВольтерраСкачать

Уравнения Вольтерра - 1Скачать

8 Последовательные приближения. Метод Монте-КарлоСкачать

Интегральные уравнения с вырожденным ядромСкачать

Простейшие интегральные уравненияСкачать




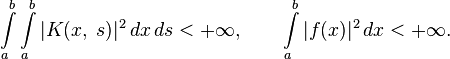
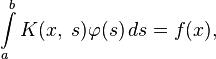
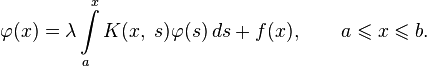
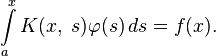

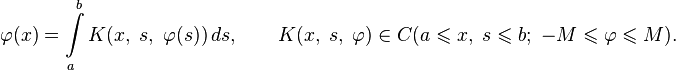

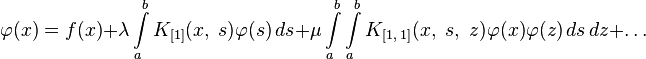

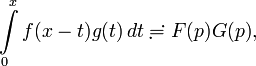
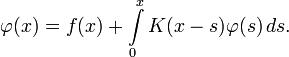

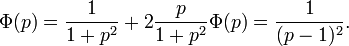
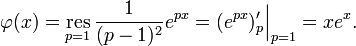


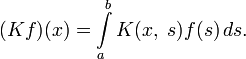
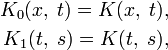





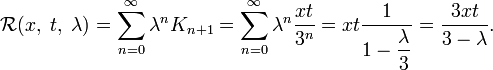


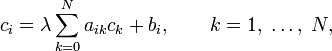

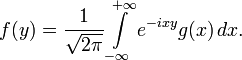

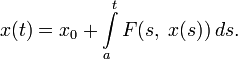

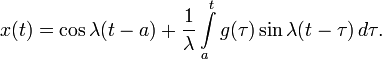
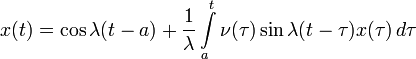
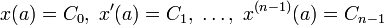

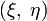 по некоторой кривой. Требуется определить эту кривую так, чтобы материальная точка, начав свое движение без начальной скорости в точке кривой с ординатой x , достигла оси Oξ за время t = f1(x) , где f1(x) — заданная функция.
по некоторой кривой. Требуется определить эту кривую так, чтобы материальная точка, начав свое движение без начальной скорости в точке кривой с ординатой x , достигла оси Oξ за время t = f1(x) , где f1(x) — заданная функция.