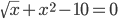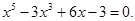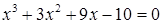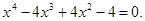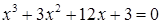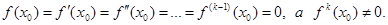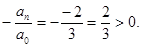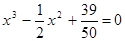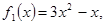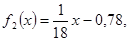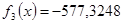Метод половинного деления решения алгебраических и трансцендентных уравнений (8 видео)

Метод половинного деления (метод дихотомии или метод бисекции)

Теорема 2. Итерационный процесс половинного деления сходится к искомому корню ξ с любой наперед заданной точностью ε.
Доказательство: Рассмотрим последовательность чисел ξ_i являющихся приближением корня на i -ом шаге.
ξ_i=½(b_i+a_i), i=0,1.
где a₀=a; b₀=b; a_i;b_i — границы подынтервалов, в которых f(a_i)f(b_i) 0 мы ни задали, всегда можно найти такое n , что ч.т.д.
Графически метод дихотомии выглядит следующим образом

|f(c)|≤δ f(a)f(c) 10 = 1024 ≈ 10 3 раз. За 20 итераций (n=2) уменьшается в 2 20 ≈ 10 6 раз.

Пример №1 . Найти экстремум функции: y=5x 2 -4x+1 методом дихотомии, если ε=0.1, а исходный интервал [0,10].

Решение
Видео решение

Пример №3 . Методом бисекции найти решение нелинейного уравнения на отрезке [a,b] с точностью ε = 10 -2 . Выбрав полученное решение в качестве начального приближения, найти решение уравнения методом простой итерации с точностью ε = 10 -4 . Для метода простой итерации обосновать сходимость и оценить достаточное для достижения заданной точности число итераций.
sqrt(t)+x 2 = 10, a = 2.6, b = 3

Найдем корни уравнения:
Используем для этого Метод половинного деления (метод дихотомии)..
Считаем, что отделение корней произведено и на интервале [a,b] расположен один корень, который необходимо уточнить с погрешностью ε.
Итак, имеем f(a)f(b) 1 /₂(a+b) и вычисляем f(c). Проверяем следующие условия:
1. Если |f(c)| 1 /₂ n (b-a)
В качестве корня ξ. возьмем 1 /₂(a_n+b_n). Тогда погрешность определения корня будет равна (b_n – a_n)/2. Если выполняется условие:
(b_n – a_n)/2 1 /₂(a_n+b_n).
Решение.
Поскольку F(2.6)*F(3) 0, то a=2.8
Итерация 2.
Находим середину отрезка: c = (2.8 + 3)/2 = 2.9
F(x) = 0.113
F(c) = -0.487
Поскольку F(c)•F(x) 0, то a=2.825
Остальные расчеты сведем в таблицу.

N	c	a	b	f(c)	f(x)
1	2.6	3	2.8	-1.6275	-0.4867
2	2.8	3	2.9	-0.4867	0.1129
3	2.8	2.9	2.85	0.1129	-0.1893
4	2.8	2.85	2.825	-0.1893	-0.3386
5	2.825	2.85	2.8375	-0.3386	-0.2641
6	2.8375	2.85	2.8438	-0.2641	-0.2267

Ответ: x = 2.8438; F(x) = -0.2267
Решение было получено и оформлено с помощью сервиса Метод Ньютона онлайн

Пример №2 . Локализовать корень нелинейного уравнения f(x) = 0 и найти его методом бисекции с точностью ε₁ = 0,01. Выбрав полученное решение в качестве начального приближения, найти решение уравнения методом простой итерации с точностью ε₂ = 0,0001. Для метода простой итерации обосновать сходимость и оценить достаточное для достижения заданной точности ε₂ число итераций.

Содержание

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО ЧИСЛЕННЫМ МЕТОДАМ — Тема: Решение алгебраических и трансцендентных уравнений методом половинного деления и методом итераций.
Лекция на тему «Метод половинного деления» план-конспект занятия
Скачать:
Предварительный просмотр:
🎦 Видео

Видео:14 Метод половинного деления Ручной счет Численные методы решения нелинейного уравненияСкачать

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО ЧИСЛЕННЫМ МЕТОДАМ — Тема: Решение алгебраических и трансцендентных уравнений методом половинного деления и методом итераций.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО ЧИСЛЕННЫМ МЕТОДАМ В СПО

Разработал преподаватель: Игнатьева Елена Сергеевна

Решение алгебраических и трансцендентных уравнений методом половинного деления и методом итераций.

— применить умения отделять корни алгебраических уравнений;

— применить умения решать алгебраические уравнений приближенными методами (метод половинного деления, метод хорд, метод касательных);

1. Рабочая тетрадь в клетку.

2. Раздаточный материал: инструкционные карты-20шт.

3. Калькулятор простой.

1. Методом половинного деления с точностью 0,01 найдите приближенное значение наибольшего действительного корня следующего алгебраического уравнения

1. Методом итераций решить уравнение с точностью до 0,001

2. Методом итераций решить с точностью до 0,001 уравнение.

1. Внимательно прочитать тему и цель практической работы .

2. Изучить учебный материал по теме.

3. Ответить на вопросы.

4. Выполнить задания.

5. Подготовить отчет.

Пояснения к работе (учебный материал):

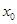
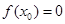
Число из области определения функции называется корнем уравнения , если .

Процесс нахождения корней уравнения распадается на несколько этапов:

1) определяются границы интервала, в котором находятся все корни уравнения ;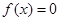

2) устанавливаются возможно малые промежутки, в каждом из которых содержатся ровно один корень.

3) каждый из корней вычисляется с заданной точностью.

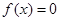
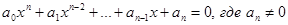
К сожалению, определение в общем виде границ интервала, в котором находятся все корни уравнения , можно дать только для алгебраического уравнения в каноническом виде, т.е. для уравнения вида:

(1)

В дальнейшем будем находить действительные корни алгебраических уравнений.

Теорема 1 (основная теорема алгебры).

Уравнения вида (1) имеет ровно n корней, действительных или комплексных, если корень кратности k считать за k корней.

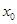
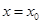
Число называется корнем кратности k уравнения (1), если при обращается в нуль сама функция и ее производные до ( k -1 )-го порядка включительно, т.е.

Корень кратности 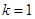называется простым.

1) Число действительных корней уравнения (1) четной степени с действительными коэффициентами всегда четно (в том числе и может равняться нулю).

Если кроме этого 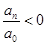, то уравнение четной степени имеет, по крайней мере, два действительных корня разного знака.

2) Уравнение (1) нечетной степени имеет по крайней мере один действительный корень того же знака, что и « ».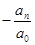

Теорема 3 (теорема Декарта).

Число положительных корней уравнения (1) равно или на четное число меньше числа перемен знака в ряду коэффициентов 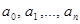уравнения. Так как при замене «х» на «-у» корни уравнения (1) меняют знаки, то с помощью этой теоремы можно оценить и число отрицательных корней.

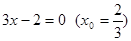
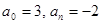
1. В уравнении нечетной степени коэффициенты и

Кроме этого, число перемен знаков равно 1.

Следовательно, по теоремам 2 и 3, оно имеет один действительный положительный корень.

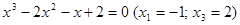
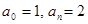
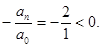
2. В уравнении нечетной степени коэффициенты и Следовательно по теореме 2, оно имеет по крайней мере один действительный отрицательный корень.

Число перемен знаков в данном уравнении равно двум, следовательно, по теореме 3, оно имеет либо два, либо 0 положительных действительных корней.

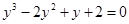
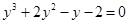
Оценим число действительных отрицательных корней. Для этого заменим «х» на «-у». Получим уравнение, или , или . Число перемен знаков в этом уравнении равно 1, следовательно, исходное уравнение имеет один действительный отрицательный корень.

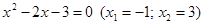
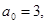
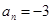
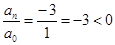
3. В уравнении четной степени коэффициенты и . Следовательно, по теореме 2, оно имеет два действительных корня разного знака.

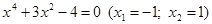
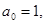
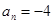
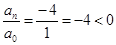
4. В уравнении четной степени коэффициенты и . Следовательно, по теореме 2, оно имеет по крайней мере два действительных корня разного знака.

Число перемен знаков в данном уравнении равно 1, следовательно, по теореме 3, оно имеет один положительный действительный корень.

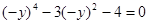
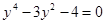
Оценим число действительных отрицательных корней. Для этого заменим «х» на «-у». Получим уравнение или . Число перемен знаков в этом уравнении равно 1, следовательно, исходное уравнение имеет один действительный корень.

Дадим теперь формулировку теоремы, позволяющей достаточно грубо определять границы интервала, в котором находятся все действительные корни уравнения (1).

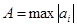
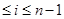
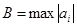
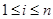
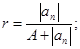
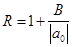
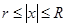
1) Если , где 0 ; , где , и , то .

2) Все положительные действительные корни уравнения находятся в промежутке , а все отрицательные действительные корни уравнения (1) находятся в промежутке .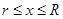

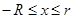
Если непрерывная и дифференцируемая функции , определяющая алгебраическое уравнение , на концах отрезка принимает значения разных знаков, т.е. , и ее первая производная сохраняет знак внутри этого отрезка, но на находится ровно один действительный корень данного уравнения.

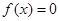
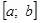
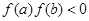
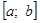
Замечание. Для алгебраических уравнений (1), степень которых больше трех, трудно аналитически находить интервалы знакопостоянства функции . Поэтому для нахождения возможно малых промежутков, содержащих ровно один действительный корень можно на практике использовать следующие способы:

1) средствами машинной графики функция представляется на дисплее и приближенно определяются возможно малые промежутки, содержащие ровно один корень (т.е. промежутки содержащие одну точку пересечения графика функции с осью Ох);

2) если график функции построить трудно, то формируют простые функции и , такие, что уравнение преобразуется в виде = . Затем строятся графики функций у= и y = и приближенно определяются промежутки, содержащие абсциссы точек пересечения этих графиков.

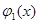
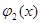
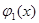
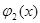
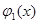
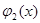
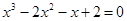
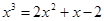
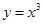
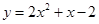
Так, например, уравнение можно преобразовать к виду и затем построить графики функции и .

Начиная третий этап, дадим формулировку теоремы, позволяющей оценивать погрешность приближенного решения.

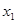
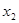
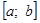
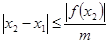
Если точный, а — приближенный, корни уравнения (1), принадлежащие одному и тому же промежутку , то справедливая оценка: , где m – наименьшее значение модуля производной функции на промежутке .

Графически решить уравнение x ln ( x )=1 .

Решение. Запишем исходное уравнение в виде: , т.е. и . Таким образом, корни данного уравнения могут быть найдены как абсциссы точек пересечения кривых и .

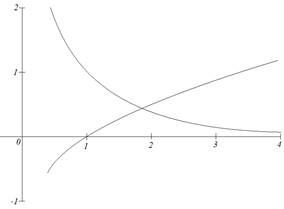
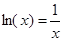
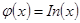
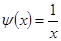
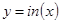
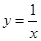
Теперь построим графики функций и определим интервал изоляции корня.

Аналитически отделить корни данного алгебраического уравнения, используя теорему Штурма:

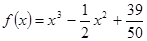
Построим таблицу для подсчета смены знаков:

—

Видео:Метод половинного деления. ДихотомияСкачать

Лекция на тему «Метод половинного деления»
план-конспект занятия

Лекция по дисциплине Численные методы для студентов специальности 09.02.07 Информационные системы и программирование

Видео:Метод половинного деления решение нелинейного уравненияСкачать

Скачать:

Вложение	Размер
Лекция по теме Метод половинного деления	129.97 КБ

Видео:Отделение корней уравнений аналитическим методом. Уточнение корней методом половинного деленияСкачать

Предварительный просмотр:

«Метод половинного деления решения алгебраических и трансцендентных уравнений»

Постановка задачи решения уравнений

Пусть имеется уравнение вида f(x)=0 , (2.1)

где f(x) — алгебраическая или трансцендентная функция.

Решить такое уравнение – значит установить, имеет ли оно корни, сколько корней, и найти значения корней (с указанной точностью).

Отделение корней алгебраических и трансцендентных уравнений

Решение указанной задачи начинается с отделения корней, т.е. с установления:

количества корней;
наиболее «тесных» промежутков, каждый из которых содержит только один корень.

Чтобы выяснить имеет ли уравнение корень:

1) Строят график функции y=f(x) для уравнения вида f(x)=0. Значения действительных корней уравнения являются абсциссами точек пересечения графиков функций y=f(x) с осью Ох.

y=f(x) кривая трижды пересекает ось абсцисс, следовательно уравнение f(x)=0 имеет три простых корня

если кривая касается оси абсцисс, то уравнение имеет двукратный корень

если кривая имеет точку перегиба, следовательно уравнение имеет трехкратных действительных корень.

2) представляют уравнение в виде f(x)=g(x) и стоят графики функции y=f(x) и y=g(x). Значения действительных корней уравнения являются абсциссами точек пересечения графиков функций у=f(х) и y=g(x). По графику определяются два числа а и b, между которыми заключен корень.

кривые y=f(x) и y=g(x) пересекаются в двух точках, абсциссы которых х 1 и х 2 являются корнями уравнения f(x)=g(x)

При решении задачи об отделении корней бывают полезными следующие очевидные положения:

Если непрерывная на отрезке [ a;b ] функция f(x) принимает на его концах значения разных знаков (т.е. f(a) . f(b) ), то уравнение (2.1) имеет на этом отрезке, по меньшей мере, один корень.
Если функция f(x) к тому же еще и монотонна, то корень на отрезке [ a;b ] единственный.

Пример: Для графического отделения корней уравнения преобразуем его к равносильному уравнению и отдельно построим графики функций .

Из рисунка видно, что графики пересекаются в одной точке, то есть уравнение имеет единственный корень х= Е и этот корень находится на отрезке [1;1,5].

Вычислим для проверки значения функции на концах отрезка [1;1,5]: f(1)=0.909298; f(1,5)= -0,264344, на концах отрезка значения функции имеют разные знаки, тогда корень на отрезке [1;1,5] действительно имеется.

Для уточнения корней можно пользоваться различными методами. Рассмотрим некоторые из них.

Метод половинного деления

Пусть уравнение (2.1) имеет на отрезке [ a;b ] единственный корень, причем функция f(x) на этом отрезке непрерывна.

1) Разделим отрезок [ a;b ] пополам точкой с=(a+b)/2 .

2) Если f(c)=0, то корень найден.

3) Если f(c)≠ 0(что практически наиболее вероятно), то нужно выбрать отрезок, на котором расположен корень. Возможны два случая: f(x) меняет знак либо на отрезке [ a;с ] (рис 2.1), либо на отрезке [ с;b ] (рис 2.2).

Рис 2.1. – функция f(x) меняет знак Рис 2.2. – функция f(x)

на отрезке [a;c] меняет знак на отрезке [c;b]

Выбирая отрезок, на котором функция меняет знак, мы выбираем отрезок, содержащий корень.

4) Этот отрезок снова делим пополам и повторяем шаги 1)-3)

Тогда, либо через конечное число делений отрезка пополам найдём точное значение корня, либо построим бесконечную последовательность вложенных отрезков:
[a; b] [a1; b1] . [an; bn], длины которых стремятся к нулю.

Как только |b n –a n |/2 E , где Е — заданная точность, то в качестве
приближённого значения корня можно взять середину этого отрезка: х=(a n +b n )/2.

Метод половинного деления требует утомительных ручных вычислений, однако он легко реализуется с помощью программы на компьютере.

Пример решения уравнений методом половинного деления

Пример: Найти корень уравнения на отрезке [1,3;1,5] с точностью до

Решение: Уравнение имеет единственный корень на отрезке [1,3;1,5].

Уточним корень уравнения: Найдем середину отрезка [1,3;1,5]: .

Определим, на каком из полученных отрезков [1,3;1,4] и [1,4;1,5] функция меняет свой знак.

Значит, корень уравнения находится на отрезке [1,3;1,4].

Проверим, достигается ли заданная точность решения 10 -4 :

, точность не достигнута.

Продолжаем процесс разделим отрезок [1,3;1,4] пополам точкой .

Определим, на каком из полученных отрезков [1,3;1,35] и [1,35;1,4] функция меняет свой знак.

Значит, корень уравнения находится на отрезке [1,35;1,4].

Проверим, достигается ли заданная точность решения 10 -4 :

, точность не достигнута.

Снова разделим отрезок [1,35;1,4] пополам точкой .

Определим, на каком из полученных отрезков [1,35;1,375] и [1,375;1,4] функция меняет свой знак.

Значит, корень уравнения находится на отрезке [1,375;1,4].

Проверим, достигается ли заданная точность решения 10 -4 :

, точность не достигнута.

Продолжая делить отрезок пополам и проверять знаки функции на новых промежутках, до тех пор, пока не будет достигнута нужная точность решения ( сделайте самостоятельно ), получим:

Решение уравнения с точностью 10 -4 : х=1,3994.

Алгоритм метода половинного деления

1) Найдем середину отрезка [a; b]: c=(a+b)/2;
2) Вычислим значения функции в точках a и c и найдем произведение полученных значений: d=f(c)*f(a);
3) Если d>0, то теперь точкой a станет c: a=c; Если d ε или

|a-b|/2> ε , то идем в пункт 1) если нет, то корень с нужной нам точностью найден, и он равен: x=(a+b)/2;