Метод половинного деления и метод хорд для численного решения уравнений

Видео:14 Метод половинного деления Ручной счет Численные методы решения нелинейного уравненияСкачать

Численные методы решения нелинейных уравнений

Если законы функционирования модели нелинейны, а моделируемые процесс или система обладают одной степенью свободы (т.е. имеют одну независимую переменную), то такая модель, как правило, описывается одним нелинейным уравнением.

Необходимость отыскания корней нелинейных уравнений встречается в расчетах систем автоматического управления и регулирования, собственных колебаний машин и конструкций, в задачах кинематического анализа и синтеза, плоских и пространственных механизмов и других задачах.

Дано нелинейное уравнение:

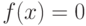( 4.1)

Необходимо решить это уравнение, т. е. найти его корень .

Если функция имеет вид многочлена степени m,

где a_i — коэффициенты многочлена, 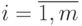, то уравнение f(x)=0 имеет m корней (рис. 4.2).

Если функция f(x) включает в себя тригонометрические или экспоненциальные функции от некоторого аргумента x , то уравнение (4.1) называется трансцендентным уравнением .

Такие уравнения обычно имеют бесконечное множество решений.

Как известно, не всякое уравнение может быть решено точно. В первую очередь это относится к большинству трансцендентных уравнений .

Доказано также, что нельзя построить формулу, по которой можно было бы решать произвольные алгебраические уравнения степени, выше четвертой.

Однако точное решение уравнения не всегда является необходимым. Задачу отыскания корней уравнения можно считать практически решенной, если мы сумеем найти корни уравнения с заданной степенью точности . Для этого используются приближенные (численные) методы решения.

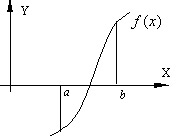
Большинство употребляющихся приближенных методов решения уравнений являются, по существу, способами уточнения корней. Для их применения необходимо знание интервала изоляции [a,b] , в котором лежит уточняемый корень уравнения (рис. 4.3).

Процесс определения интервала изоляции [a,b] , содержащего только один из корней уравнения, называется отделением этого корня.

Процесс отделения корней проводят исходя из физического смысла прикладной задачи, графически, с помощью таблиц значений функции f(x) или при помощи специальной программы отделения корней. Процедура отделения корней основана на известном свойстве непрерывных функций: если функция непрерывна на замкнутом интервале [a,b] и на его концах имеет различные знаки, т.е. f(a)f(b) , то между точками a и b имеется хотя бы один корень уравнения (1). Если при этом знак функции f'(x) на отрезке [a,b] не меняется, то корень является единственным на этом отрезке.

Процесс определения корней алгебраических и трансцендентных уравнений состоит из 2 этапов:

1. отделение корней, — т.е. определение интервалов изоляции [a,b] , внутри которого лежит каждый корень уравнения;
2. уточнение корней, — т.е. сужение интервала [a,b] до величины равной заданной степени точности .

Для алгебраических и трансцендентных уравнений пригодны одни и те же методы уточнения приближенных значений действительных корней:

Видео:Метод половинного деления решение нелинейного уравненияСкачать

Метод половинного деления и метод хорд для численного решения уравнений

Nickolay.info. Обучение. Лекции по численным методам. Приближённое решение нелинейных алгебраических уравнений

1. Приближенное решение нелинейных алгебраических уравнений

Дано нелинейное алгебраическое уравнение

Нелинейность уравнения означает, что график функции не есть прямая линия, т.е. в f(x) входит x в некоторой степени или под знаком функции.

Решить уравнение – это найти такое x* ∈ R: f(x*)=0. Значение x* называют корнем уравнения. Нелинейное уравнение может иметь несколько корней. Геометрическая интерпретация корней уравнения представлена на рис. 1. Корнями уравнения (1) являются точки x₁*, x₂*, x₃*, в которых функция f(x) пересекает ось x.

Методы решения нелинейного уравнения (1) можно разделить на точные (аналитические) и приближенные (итерационные). В точных методах корень представляется некоторой алгебраической формулой. Например, решение квадратных уравнений, некоторых тригонометрических уравнений и т. д.

В приближенных методах процесс нахождения решения, вообще говоря, бесконечен. Решение получается в виде бесконечной последовательности <x_n>, такой, что . По определению предела, для любого (сколь угодно малого) ε, найдется такое N, что при n>N, |x_n – x*| / (x) не меняет знак на отрезке [a, b], т.е. f(x) – монотонная функция, в этом случае отрезок [a,b] будет интервалом изоляции.

Если корней несколько, то для каждого нужно найти интервал изоляции.

Существуют различные способы исследования функции: аналитический, табличный, графический.

Аналитический способ состоит в нахождении экстремумов функции f(x), исследование ее поведения при и нахождение участков возрастания и убывания функции.

Графический способ – это построение графика функции f(x) и определение числа корней по количеству пересечений графика с осью x.

Табличный способ – это построение таблицы, состоящей из столбца аргумента x и столбца значений функции f(x). О наличии корней свидетельствуют перемены знака функции. Чтобы не произошла потеря корней, шаг изменения аргумента должен быть достаточно мелким, а интервал изменения достаточно широким.

Решить уравнение x 3 ‑ 6x 2 +3x+11=0, т.е. f(x)= x 3 ‑ 6x 2 +3x+11.

Найдем производную f / (x)=3x 2 -12x+3.

Найдем нули производной f / (x)=3x 2 -12x+3=0; D=144-4*3*3=108;

X₁== 0.268;

X₂== 3.732;

Так как f / ()>0, то f / (x)>0 при , f / (x) / (x)>0 при . Кроме того, f()= 0. Следовательно, на интервале возрастает от до f(x₁)= 3x₁ 2 -12x₁+3=11.39; на интервале — убывает до f(x₂)= 3x₂ 2 -12x₂+3=-9.39 и на интервале возрастает до , т.е. уравнение имеет три корня.

Найдем интервалы изоляции для каждого из корней.

Рассмотрим для первого корня отрезок [-2, -1]:

f(-2)= -27 0, f / (x)>0 при т.е. этот отрезок является интервалом изоляции корня.

Рассмотрим для второго корня отрезок [1, 3]:

f(1)= 9>0, f(3)= -7 / (x) 0, f / (x)>0 при т.е. этот отрезок является интервалом изоляции корня.

Видео:Метод половинного деления. ДихотомияСкачать

Численные методы решения нелинейных уравнений. Метод хорд.

Видео:8 Метод половинного деления Calc Excel Численные методы решения нелинейного уравненияСкачать

Численные методы решения нелинейных уравнений. Метод хорд.

Метод хорд ( метод также известен как Метод секущих ) один из методов решения нелинейных уравнений и основан на последовательном сужении интервала, содержащего единственный корень уравнения . Итерационный процесс выполняется до того момента, пока не будет достигнута заданная точность .

В отличие от метода половинного деления, метод хорд предлагает, что деление рассматриваемого интервала будет выполняться не в его середине, а в точке пересечения хорды с осью абсцисс (ось — Х). Следует отметить, что под хордой понимается отрезок, который проведен через точки рассматриваемой функции по концам рассматриваемого интервала. Рассматриваемый метод обеспечивает более быстрое нахождение корня, чем метод половинного деления, при условии задания одинакового рассматриваемого интервала.

Геометрически метод хорд эквивалентен замене кривой хордой, проходящей через точки и (см. рис.1.).

Рис.1. Построение отрезка (хорды) к функции .

Уравнение прямой (хорды), которая проходит через точки А и В имеет следующий вид:

Данное уравнение является типовым уравнением для описания прямой вы декартовой системе координат. Наклон кривой задается по ординате и абсциссе с помощью значений в знаменателе и , соответственно.

Для точки пресечения прямой с осью абсцисс записанное выше уравнение перепишется в следующем виде:

В качестве нового интервала для прохождения итерационного процесса выбираем один из двух или , на концах которого функция принимает значения разных знаков. Противоположность знаков значений функции на концах отрезка можно определить множеством способов. Один из множества этих способов — умножение значений функции на концах отрезка и определение знака произведения путём сравнения результата умножения с нулём:

или .

Итерационный процесс уточнения корня заканчивается, когда условие близости двух последовательных приближений станет меньше заданной точности, т.е.

.

Рис.2. Пояснение к определению погрешности расчета.

Следует отметить, что сходимость метода хорд линейная, однако более быстрая, чем сходимость метода половинного деления.

Алгоритм нахождения корня нелинейного уравнения по методу хорд

1. Найти начальный интервал неопределенности одним из методов отделения корней. З адать погрешность расчета (малое положительное число ) и начальный шаг итерации ( ) .

2. Найти точку пересечения хорды с осью абсцисс:

3. Необходимо найти значение функции в точках , и . Далее необходимо проверить два условия:

— если выполняется условие , то искомый корень находится внутри левого отрезка положить , ;

— если выполняется условие , то искомый корень находится внутри правого отрезка принять , .

В результате находится новый интервал неопределенности, на котором находится искомых корень уравнения:

4. Проверяем приближенное значение корня уравнения на предмет заданной точности, в случае:

— если разность двух последовательных приближений станет меньше заданной точности , то итерационный процесс заканчивается. Приближенное значение корня определяется по формуле:

— если разность двух последовательных приближений не достигает необходимой точности , то необходимо продолжить итерационный процесс и перейти к п.2 рассматриваемого алгоритма.

Видео:Метод половинного деленияСкачать

Пример решения уравнений методом хорд

В качестве примера, рассмотрим решение нелинейного уравнения методом хорд. Корень необходимо найти в рассматриваемом диапазоне с точностью .

Вариант решения нелинейного уравнения в программном комплексе MathCAD .

Результаты расчетов, а именно динамика изменения приближенного значения корня, а также погрешности расчета от шага итерации представлены в графической форме (см. рис.1).

Рис.1. Результаты расчета по методу хорд

Для обеспечения заданной точности при поиске уравнения в диапазоне необходимо выполнить 6 итераций. На последнем шаге итерации приближенное значение корня нелинейного уравнения будет определяться значением: .

Примечание:

Модификацией данного метода является метод ложного положения ( False Position Method ), который отличается от метода секущих только тем, что всякий раз берутся не последние 2 точки, а те точки, которые находятся вокруг корня.

Следует отметить, что в случае если от нелинейной функции можно взять вторую производную алгоритм поиска может быть упрощен. Предположим, что вторая производная сохраняет постоянный знак, и рассмотрим два случая:

Случай №1: 0,

f»(a)>0″ width=»158″ height=»20″ border=»0″ />

Из первого условия получается, что неподвижной стороной отрезка является – сторона a .

Случай №2: 0″ width=»158″ height=»20″ border=»0″ />

Из второго условия получается, что неподвижной стороной отрезка является – сторона b .

В общем виде, для выявления неподвижного конца можно записать следующее условие: 0″ width=»122″ height=»20″ border=»0″ /> , где или .

Рис. 3. Примеры убывающей или возрастающей функции

Таким образом, в зависимости от вида функции получаются два выражения для упрощения поиска корня функции:

— если функция соответствует первому случаю (см. рис. 3), тогда формула будет иметь следующий вид:

, где k =0,1,2,…

— если функция соответствует второму случаю (см. рис. 3), тогда формула будет иметь следующий вид:

, где k =0,1,2,…

Случай сводится к рассматриваемому , если уравнение записать в форме: .

Для того, чтобы добавить Ваш комментарий к статье, пожалуйста, зарегистрируйтесь на сайте.

🔍 Видео

Численные методы решения нелинейного уравнени Теория Шаговый Метод половинного деления Метод НьютонаСкачать

7 Метод половинного деления Mathcad Численные методы решения нелинейного уравненияСкачать

Решение нелинейного уравнения методом половинного деления (программа)Скачать

Численное решение уравнений, урок 3/5. Метод хордСкачать

1,2 Решение нелинейных уравнений методом хордСкачать

Метод хордСкачать

12й класс; Информатика; "Численные методы. Метод половинного деления"Скачать

Метод половинного деления Ручной счет Численные методы решения нелинейного уравненияСкачать

3 Теория: Численные методы решения нелинейного уравнения Шаговый, половинного деления, НьютонаСкачать

6 Метод половинного деления C++ Численные методы решения нелинейного уравненияСкачать

Решение нелинейных уравнений методом хордСкачать

5.1 Численные методы решения уравнений F(x)=0Скачать

Решение нелинейного уравнения методом половинного деления (дихотомии)Скачать

Метод Ньютона (метод касательных) Пример РешенияСкачать

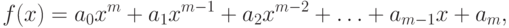
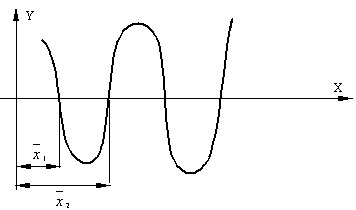
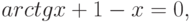
Метод дихотомииСкачать