1. Постановка задачи 3
2. Анализ задачи 3
3. Схема алгоритма. 6
4. Текст программы на Паскале 7
5. Результаты расчёта 8
7. Список литературы 9
1. Постановка задачи
Создать программный продукт, который находит искомый корень уравнения в отрезке при помощи метода половинного деления.
Метод половинного деления.
Для этого метода существенно, чтобы функция f(x) была непрерывна и ограничена в заданном интервале [a, b], внутри которого находится корень. Предполагается также, что значения функции на концах интервала f(a) и f(b) имеют разные знаки, т.е. выполняется условие f(a)f(b) .
Обозначим исходный интервал [a, b] как [a0, b0]. Для нахождения корня уравнения f(x) = 0 отрезок [a0, b0] делится пополам, т.е. вычисляется начальное приближение x0 = (a0 + b0)/2. Если f(x0) = 0, то значение x0 = x* является корнем уравнения. В противном случае выбирается один из отрезков [a0, x0] или [x0, b0], на концах которого функция f(x) имеет разные знаки, так как корень лежит в этой половине. Далее выбранный отрезок обозначается как [a1, b1], вновь делится пополам точкой x1 = (a1 + b1)/2 и т.д. В результате на некоторой итерации получается точный корень x* уравнения f(x) = 0, либо бесконечная последовательность вложенных отрезков [a0, b0], [a1, b1], ., [ai, bi], ., таких, что f(ai)f(bi) (i =1, 2, .), сходящихся к корню x*.
Если требуется определить корень x* с погрешностью , то деление исходного интервала [a, b] продолжают до тех пор, пока длина отрезка [ai, bi] не станет меньше 2, что записывается в форме условия bi — ai 2.
В этом случае середина последнего интервала [ai, bi] с требуемой степенью точности дает приближенное значение корня
Метод половинного деления легко реализуется на ЭВМ и является наиболее универсальным среди итерационных методов уточнения корней. Его применение гарантирует получение решения для любой непрерывной функции f(x), если найден интервал, на котором она изменяет знак. В том случае, когда корни не отделены, будет найден один из корней уравнения. Метод всегда сходится, но скорость сходимости является небольшой, так как за одну итерацию точность увеличивается примерно в два раза. Поэтому на практике метод половинного деления обычно применяется для грубого нахождения корней уравнения, поскольку при повышении требуемой точности значительно возрастает объем вычислений.
- Метод половинного деления
- Презентация к уроку «Приближенное решение уравнений. Метод половинного деления»
- Описание презентации по отдельным слайдам:
- Краткое описание документа:
- Дистанционное обучение как современный формат преподавания
- Инструменты онлайн-обучения на примере программ Zoom, Skype, Microsoft Teams, Bandicam
- Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС
- Дистанционные курсы для педагогов
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- 📺 Видео
Видео:Метод половинного деления решение нелинейного уравненияСкачать

Метод половинного деления
Домашняя лабораторная работа по теме «Приближенное решение уравнений с одной переменной»
Задание. Найти один из корней уравнения методом деления отрезка пополам (методом Фибоначчи, «золотого сечения», рандомизации) с точностью до 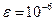

Порядок выполнения работы
1) Графическое отделение корня в случае достаточно сложного выражения y=f(х) можно производить следующим образом. Допустим, что уравнение можно представить в виде f1(x) = f2(x). В этом случае строим графики функций у=f1(x) и y=f2(x); абсциссы точек пересечения кривых будут действительными корнями уравнения. Найдем, например, приближенно корни уравнения x-sin x-1 = 0, записав это уравнение в виде x-1 = sin x. Построим графики функций y = sin x и у = х-1 (рис.2). Точка пересечения этих линий имеет абсциссу х ≈ 1,9, что можно считать грубым приближением значения корня.
Интервал [а;b] является интервалом изоляции корня, если его можно считать настолько малым, что на нем лежит точно один корень исходного уравнения. Выбор этого интервала производится на основании свойства непрерывных функций: если функция у=f(x) непрерывна на отрезке [а;b] и на концах отрезка принимает значения разных знаков (f(a)f(b) 3 +x 2 -1=0. Для этого представим уравнение в виде: х 3 =1-x 2 , т. е. f(x)=x 3 и g(x)=1-x 2 . Построим приближенно графики функций y=f(x) и y=g(x) (рис 4). Точка пересечения графиков двух функций, а значит, и корень уравнения находится на отрезке [0;1]. Проверим аналитические условия: f(0)=0 3 +0 2 -1=-1 3 +1 2 -1=1>0, и f'(х)=3х²+2x>0 на отрезке [0;1]. Таким образом, мы определили интервал изоляции корня, для нахождения которого достаточно применить любой из аналитических методов численного решения уравнений.
Задача отыскания корней уравнений может считаться практически решенной, если удалось определить корни с нужной степенью точности и указать пределы возможной погрешности.
Метод половинного деления
Рассмотрим один из самых простых численных методов решения уравнений – метод половинного деления. Пусть для уравнения 
Рассмотрим применение метода половинного деления на примере решения уравнения х 3 +x 2 -1 = 0 на отрезке [0;1]. Разделим интервал изоляции пополам – это точка х=0,5. Получим два подотрезка – [0;0,5] и [0,5;1]. Вычислим значения функции на концах отрезков, f(0)=-1 3 +0,5 2 -1=0,125+0,25-1=-0,625 3 +1 2 -1=1+1—1=1>0, т. е. на концах отрезка [0,5;1] функция имеет значения разных знаков, следовательно, корень уравнения принадлежит отрезку [0,5;1]. Выбираем этот отрезок для дальнейшего рассмотрения.
Повторяем метод половинного деления уже для нового отрезка. Середина отрезка x=(0,5+1)/2=0,75, и из двух полученных отрезков выбираем правый отрезок [0,75;1], т.к. f(0,75) = -0,015625 0. Процесс продолжается до получения корня с заданной степенью точности.
Если делить отрезок [a;b] сразу на десять частей, то на следующем шаге можно получить отрезок в десять раз меньший, чем [a;b].
2. Метод Фибоначчи
Рассмотрим одну из разновидностей метода половинного деления – метод Фибоначчи.
Пусть дано уравнение 








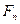







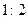


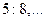




Видео:Решение нелинейного уравнения методом половинного деления (программа)Скачать

Презентация к уроку «Приближенное решение уравнений. Метод половинного деления»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Описание презентации по отдельным слайдам:
ПРИБЛИЖЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ МЕТОД ПОЛОВИННОГО ДЕЛЕНИЯ
ПРИБЛИЖЕННОЕ РЕШЕНИЕ На языке алгебры формальные модели записываются с помощью уравнений, точные решения которых существуют только для некоторых уравнений определенного вида (линейные, квадратные, тригонометрические и др.). Для большинства уравнений приходится использовать методы приближенного решения с заданной точностью.
ГРАФИЧЕСКИЕ МЕТОДЫ Уравнение нельзя решить путем равносильных алгебраических преобразований. Такие решения можно решать приближенно графическими и численными методами. Построим графики функций и
ОТДЕЛЕНИЕ КОРНЕЙ С помощью графиков определяем координаты концов отрезков, содержащих точки пересечения графиков. a=0, b=1,5
Отрезок [a;b] делится пополам c=(a+b)/2. Выбираем отрезок [a;c] или [c;b], проверяя знаки значений функции на концах отрезков. f(a)*f(c) = eps do begin. » onclick=»aa_changeSlideByIndex(7, 0, true)» >
Begin clrscr; a:=0; b:=1.5; eps:=0.0001; while abs(f(a)-f(b)) >= eps do begin c:=(a+b)/2; if f(a)*f(c)
Краткое описание документа:
Презентация может быть использована при изучении темы «Моделирование» в 11 классе. В презентации вводятся понятия приближенного решения уравнений, точности вычисления, рассматриваются графический метод решения уравнений, метод отделения корней уравнения, метод половинного деления отрезка. В презентации представлена программа на языке Паскаль для решения уравнения методом половинного деления, а также описание выполнения вычислений в электронных таблицах с подробной инструкцией. В электронных таблицах приближенное решение уравнения ведется через подбор параметра.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 930 человек из 80 регионов
Курс повышения квалификации
Инструменты онлайн-обучения на примере программ Zoom, Skype, Microsoft Teams, Bandicam
- Курс добавлен 31.01.2022
- Сейчас обучается 26 человек из 18 регионов
Курс повышения квалификации
Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС
- Сейчас обучается 36 человек из 23 регионов
Ищем педагогов в команду «Инфоурок»
Видео:12й класс; Информатика; "Численные методы. Метод половинного деления"Скачать

Дистанционные курсы для педагогов
«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»
Свидетельство и скидка на обучение каждому участнику
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 594 911 материалов в базе
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
«Психологические методы развития навыков эффективного общения и чтения на английском языке у младших школьников»
Свидетельство и скидка на обучение каждому участнику
Другие материалы
- 22.09.2014
- 1066
- 1
- 22.09.2014
- 1232
- 0
- 22.09.2014
- 747
- 0
- 22.09.2014
- 7038
- 13
- 21.09.2014
- 1718
- 3
- 21.09.2014
- 2618
- 1
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 22.09.2014 4470
- PPTX 986 кбайт
- 26 скачиваний
- Рейтинг: 4 из 5
- Оцените материал:
Настоящий материал опубликован пользователем Марданова Гульсина Насиховна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 6 лет и 7 месяцев
- Подписчики: 0
- Всего просмотров: 3850
- Всего материалов: 1
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Видео:Метод половинного деления - ВизуализацияСкачать

Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Школьник из Сочи выиграл международный турнир по шахматам в Сербии
Время чтения: 1 минута
В Белгородской области отменяют занятия в школах и детсадах на границе с Украиной
Время чтения: 0 минут
Минпросвещения России подготовит учителей для обучения детей из Донбасса
Время чтения: 1 минута
Курские власти перевели на дистант школьников в районах на границе с Украиной
Время чтения: 1 минута
В Швеции запретят использовать мобильные телефоны на уроках
Время чтения: 1 минута
Минобрнауки и Минпросвещения запустили горячие линии по оказанию психологической помощи
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
📺 Видео
Метод половинного деления. ДихотомияСкачать

Урок 10. C++ Метод половинного деленияСкачать

Метод половинного деленияСкачать

14 Метод половинного деления Ручной счет Численные методы решения нелинейного уравненияСкачать

Метод половинного деления Ручной счет Численные методы решения нелинейного уравненияСкачать

7 Метод половинного деления Mathcad Численные методы решения нелинейного уравненияСкачать

6 Метод половинного деления C++ Численные методы решения нелинейного уравненияСкачать

Алгоритмы. Нахождение корней уравнений методом деления отрезка пополам.Скачать

8 Метод половинного деления Calc Excel Численные методы решения нелинейного уравненияСкачать

Отделение корней уравнений аналитическим методом. Уточнение корней методом половинного деленияСкачать

5 Метод половинного деления Блок-схема Численные методы решения нелинейного уравненияСкачать

Численные методы решения нелинейного уравнени Теория Шаговый Метод половинного деления Метод НьютонаСкачать

Метод дихотомииСкачать

1.1 Решение нелинейных уравнений метод деления отрезка пополам (бисекций) Мathcad15Скачать

Метод дихотомии c++Скачать

Решение нелинейного уравнения методом половинного деления (дихотомии)Скачать







