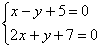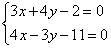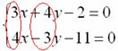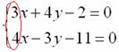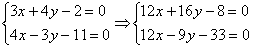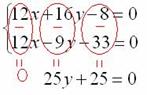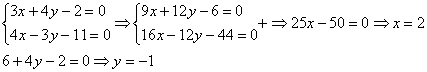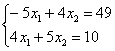Метод почленного сложения вычитания уравнений системы (4 видео)

Решение системы методом почленного сложения (вычитания) уравнений системы

В ходе решения систем линейных уравнений нужно стараться использовать не «школьный метод», а метод почленного сложения (вычитания) уравнений системы. Почему? Это экономит время и упрощает вычисления, как сейчас увидите.

Пример 4:

Решить систему линейных уравнений:

Мы взяли ту же систему, что и в первом примере.

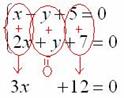
Анализируя систему уравнений, замечаем, что коэффициенты при переменной y одинаковы по модулю и противоположны по знаку (–1 и 1). В такой ситуации уравнения можно сложить почленно:

Действия, обведенные красным цветом, выполняются МЫСЛЕННО. Как видите, в результате почленного сложения у нас пропала переменная y.

В этом и состоит суть метода – избавиться от одной из переменных.

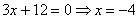
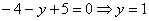
Теперь всё просто: – подставляем в первое уравнение системы (можно и во второе, но это не так выгодно – там числа больше):

В чистовом оформлении решение должно выглядеть примерно так:

Ответ: x = -4, y = 1.

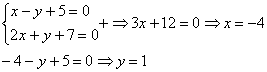
Пример 5:

Решить систему линейных уравнений:

В данном примере можно использовать «школьный» метод, но большой минус состоит в том, что когда мы будем выражать какую-либо переменную из любого уравнения, то получим решение в обыкновенных дробях. А возня с дробями займет время, к тому же, если у Вас не «набита рука» на действиях с дробями, то велика вероятность допустить ошибку.

Поэтому целесообразно использовать почленное сложение (вычитание) уравнений. Анализируем коэффициенты при соответствующих переменных:

Как видим, числа в парах (3 и 4), (4 и –3) – разные, поэтому, если сложить (вычесть) уравнения прямо сейчас, то от переменной мы не избавимся. Хотелось бы видеть в одной из пар одинаковые по модулю числа, например, 20 и 20 либо 20 и –20.

Будем рассматривать коэффициенты при переменной x:

Подбираем такое число, которое делилось бы и на 3 и на 4, причем оно должно быть как можно меньше. В математике такое число называется наименьшим общим кратным. Если Вы затрудняетесь с подбором, просто перемножьте коэффициенты: 3∙4 = 12.

Далее первое уравнение умножаем на число

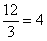
Второе уравнение умножаем на число 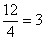. В результате система придет к виду:

Вот теперь из первого уравнения почленно вычитаем второе.

На всякий случай приведём еще раз действия, которые проводятся мысленно:

Следует отметить, что можно было бы сделать и наоборот – из второго уравнения вычесть первое, это ничего не меняет. Начисто запишем:

Теперь подставим вычисленное значение переменной (y) в одно из уравнений системы. Например, в первое:

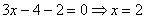
Ответ: .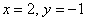

Решим систему другим способом. Рассмотрим коэффициенты при переменной (y):

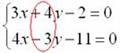
Очевидно, что вместо пары коэффициентов (4 и –3) нам нужно получить 12 и –12.

Для этого первое уравнение умножаем на 3, второе уравнение умножаем на 4:

Почленно складываем уравнения и находим значения переменных:

Ответ:

Пример 6:

Решить систему линейных уравнений:

Это пример для самостоятельного решения (ответ в конце урока).

Содержание

Как решается система уравнений? Методы решения систем уравнения.
Решим методом подстановки
Решим методом почленного сложения (вычитания).
Линейные уравнения. Решение систем линейных уравнений. Способ сложения.
💥 Видео

Видео:Решение систем уравнений методом сложенияСкачать

Как решается система уравнений? Методы решения систем уравнения.

Методы решения систем уравнения.

Разберем два вида решения систем уравнения:

1. Решение системы методом подстановки.
2. Решение системы методом почленного сложения (вычитания) уравнений системы.

Для того чтобы решить систему уравнений методом подстановки нужно следовать простому алгоритму:
1. Выражаем. Из любого уравнения выражаем одну переменную.
2. Подставляем. Подставляем в другое уравнение вместо выраженной переменной, полученное значение.
3. Решаем полученное уравнение с одной переменной. Находим решение системы.

Чтобы решить систему методом почленного сложения (вычитания) нужно:
1.Выбрать переменную у которой будем делать одинаковые коэффициенты.
2.Складываем или вычитаем уравнения, в итоге получаем уравнение с одной переменной.
3. Решаем полученное линейное уравнение. Находим решение системы.

Решением системы являются точки пересечения графиков функции.

Рассмотрим подробно на примерах решение систем.

Решим методом подстановки

2x+5y=1 (1 уравнение)
x-10y=3 (2 уравнение)

1. Выражаем
Видно что во втором уравнении имеется переменная x с коэффициентом 1,отсюда получается что легче всего выразить переменную x из второго уравнения.
x=3+10y

2.После того как выразили подставляем в первое уравнение 3+10y вместо переменной x.
2(3+10y)+5y=1

3.Решаем полученное уравнение с одной переменной.
2(3+10y)+5y=1 (раскрываем скобки )
6+20y+5y=1
25y=1-6
25y=-5 |: (25)
y=-5:25
y=-0,2

Решением системы уравнения является точки пересечений графиков, следовательно нам нужно найти x и у, потому что точка пересечения состоит их x и y.Найдем x, в первом пункте где мы выражали туда подставляем y.
x=3+10y
x=3+10*(-0,2)=1

Точки принято записывать на первом месте пишем переменную x, а на втором переменную y.
Ответ: (1; -0,2)

Решим методом почленного сложения (вычитания).

3x-2y=1 (1 уравнение)
2x-3y=-10 (2 уравнение)

1.Выбираем переменную, допустим, выбираем x. В первом уравнении у переменной x коэффициент 3, во втором 2. Нужно сделать коэффициенты одинаковыми, для этого мы имеем право домножить уравнения или поделить на любое число. Первое уравнение домножаем на 2, а второе на 3 и получим общий коэффициент 6.

2.Из первого уравнения вычтем второе, чтобы избавиться от переменной x.Решаем линейное уравнение.
__6x-4y=2

3.Находим x. Подставляем в любое из уравнений найденный y, допустим в первое уравнение.
3x-2y=1
3x-2*6,4=1
3x-12,8=1
3x=1+12,8
3x=13,8 |:3
x=4,6

Точкой пересечения будет x=4,6; y=6,4
Ответ: (4,6; 6,4)

Хочешь готовиться к экзаменам бесплатно? Репетитор онлайн бесплатно. Без шуток. ЗДЕСЬ

Видео:Решение систем уравнений методом сложенияСкачать

Линейные уравнения. Решение систем линейных уравнений. Способ сложения.

Метод сложения – решая системы линейных уравнений методом сложения, уравнения системы почленно складывают, при этом 1-но либо оба (несколько) уравнений можно умножить на любое число. В результате приходят к равнозначной СЛУ, где в одном из уравнений есть лишь одна переменная.

Для решения системы способом почленного сложения (вычитания) следуйте следующим шагам:

1. Выбираем переменную, у которой будут делаться одинаковые коэффициенты.

2. Теперь нужно сложить либо вычесть уравнения и получим уравнение с одной переменной.

3. Далее необходимо решить линейное уравнение, которое мы получили и найти решение системы.

Решение системы — это точки пересечения графиков функции.

Рассмотрим на примерах.

Проанализировав эту систему можно заметить, что коэффициенты при переменной равны по модулю и разные по знаку (–1 и 1). В таком случае уравнения легко сложить почленно:

Действия, которые обведены красным цветом, выполняем в уме.

Результатом почленного сложения стало исчезновение переменной y. Именно в этом и В этом, собственно, и заключается смысл метода – избавиться от 1-ой из переменных.

Далее очень легко: 3x + 12 = 0 → x = -4 – подставляем в 1-е уравнение системы (можете и во 2-у, но это не так удобно, так как во втором уравнении числа больше):

В виде системы решение выглядит где-то так:

В этом примере можете пользоваться «школьным» методом, но в нем есть немаленький минус — когда вы будете выражать любую переменную из любого уравнения, то получите решение в обыкновенных дробях. А решение дробей занимает достаточно времени и вероятность допущения ошибок увеличивается.

Поэтому лучше пользоваться почленным сложением (вычитанием) уравнений. Проанализируем коэффициенты у соответствующих переменных:

Нужно подобрать число, которое можно поделить и на 3 и на 4, при этом нужно, что бы это число было минимально возможным. Это наименьшее общее кратное. Если вам тяжело подобрать подходящее число, то можете перемножить коэффициенты: .