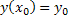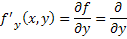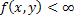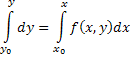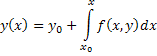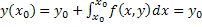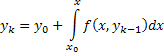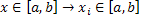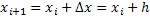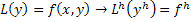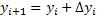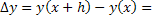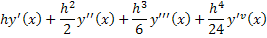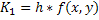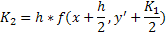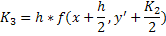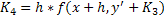Метод пикара для решения дифференциального уравнения (6 видео)

Метод последовательных приближений решения дифференциального уравнения

Пусть требуется найти решение дифференциального уравнения

Будем предполагать, что в некотором прямоугольнике для уравнения (1) выполнены условия а) и б) теоремы существования и единственности решения задачи (1)-(2).

Решение задачи (1)-(2) может быть найдено методом последовательных приближений , который состоит в следующем.

Строим последовательность функций, определяемых рекуррентными соотношениями

В качестве нулевого приближения можно взять любую функцию, непрерывную в окрестности точки , в частности — начальное значение Коши (2). Можно доказать, что при сделанных предположениях относительно уравнения (1) последовательные приближения сходятся к точному решению уравнения (1), удовлетворяющему условию (2), в некотором интервале , где

Оценка погрешности, получаемой при замене точного решения n-м приближением , даётся неравенством

где . Применяя метод последовательных приближений, следует остановиться на таком , для которого не превосходит допустимой погрешности.

Пример 1. Методом последовательных приближений найти решение уравнения , удовлетворяющее начальному условию .

Решение. Очевидно, что для данного уравнения на всей плоскости выполнены условия теоремы существования и единственности решения задачи Коши. Строим последовательность функций, определяемых соотношениями (3), приняв за нулевое приближение :

Ясно, что при . Непосредственной проверкой убеждаемся, что функция решает поставленную задачу Коши.

Пример 2. Методом последовательных приближений найти приближенное решение уравнения , удовлетворяющее начальному условию в прямоугольнике

Решение. Имеем , т. е. . За берем меньшее из чисел , т. е. . Последовательные приближения согласно (4) будут сходится в интервале . Составляем их

Абсолютная погрешность третьего приближения не превосходит величины

Замечание. Функция должна удовлетворять всем условиям теоремы существования и единственности решения задачи Коши.

Следующий пример показывает, что одной непрерывности функции недостаточно для сходимости последовательных приближений.

Пусть функция определена следующим образом:

На множестве , функция непрерывна и ограничена постоянной . Для начальной точки последовательные приближения при имеют вид:

Поэтому последовательность для каждого не имеет, предела, т. е. последовательные приближения не сходятся. Заметим также, что ни одна из сходящихся подпоследовательностей и не сходится к решению, поскольку

Если же последовательные приближения сходятся, то полученное решение может оказаться неединственным , как показывает следующий пример: .

Возьмем начальное условие ; тогда

Беря в качестве нулевого приближения функцию , будем иметь

так что все последовательные приближения равны нулю и поэтому они сходятся к функции, тождественно равной нулю. С другой стороны, функция представляет собой также решение этой задачи, существующее на полупрямой .

Видео:5. Метод последовательных приближенийСкачать

метод последовательных приближений

М етод последовательных приближений (или метод Пикара) является аналитическим, т. е. позволяет получить приближённое решение задачи Коши, определяемой дифференциальным уравнением (1) с начальным условием (2), в виде формулы. Возник метод в связи с доказательством теоремысуществования и единственности решения задачи Коши (гл. 1).

Пусть в условиях данной теоремы требуется найти решение уравнения (1) с начальным условием (2). Проинтегрируем обе части уравнения (1) от х₀ доx:

, откуда

у(х) = у₀ + . (7)

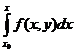
Очевидно, что решение интегрального уравнения (7) будет удовлетворять уравнению (1) и начальному условию (2). Действительно, при х =х₀ получим

у(х₀) = у₀ + 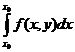= у₀.

Применим к интегральному уравнению (7) метод последовательных приближений. Заменим в равенстве (7) неизвестную функцию у данным значением у₀, получим первое приближение

у₁(х) = у₀ + .

Заметим, что интеграл в правой части содержит только одну переменную х, поэтому аналитическое выражение первого приближения у₁(х) будет являться функцией, зависящей
от х.Заменим теперь в равенстве (7) неизвестную функцию у найденным значением у₁(х), получим второе приближение

у₂(х) = у₀ +

и т. д. В общем случае итерационная формула имеет вид

у_n(х) = у₀ + ( n =1, 2, . ). (8)

Применив неоднократно формулу (8), получим последовательность функций

Можно доказать [1, 2, 3], что эта последовательность сходится и

= у(х),

т.е. предел последовательности является решением интегрального уравнения (7), а следовательно, и дифференциального уравнения (1) с начальным условием (2). Это означает, что k-й член последовательности (9) является приближением к точному решению уравнения (1)
с определённой степенью точности.

Погрешность k-го приближения можно оценить формулой

, (10)

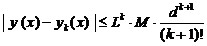
где L — постоянная Липшица; М — верхняя грань модуля функции f, т.е. ;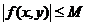

величина d для определения окрестности 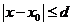вычисляется по формуле , числаа и b— из неравенства Липшица (гл. 1).

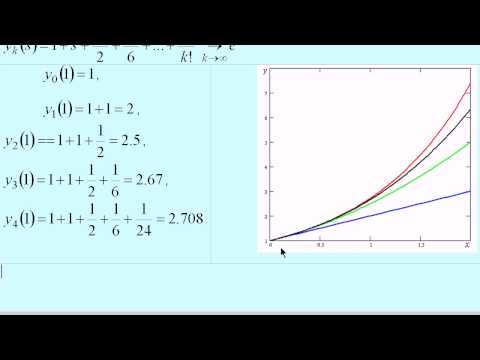
Пример 1. Найти три последовательных приближения решения дифференциального уравнения у’ = x + y 2 ,удовлетворяющего начальному условию у(0) = 1.

Решение.В качестве начального приближения возьмём

первое приближение у₁(х) = у₀ + = 1+ ,

второе приближение у₂(х) = у₀ + = 1+ ,

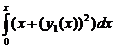
третье приближение у₃(х) = у₀ + = 1+ .

Вычисления интегралов и построение графиков полученных функций у₁(х), у₂(х), у₃(х) проведём в системе MathCAD. Результаты решения представлены на рис. 14.

Оценим погрешность третьего приближения.

Для определения области G, заданной неравенствами (6), примема = 1, b = 2. Получим

G: – 1 х 1,–1 y 3.

В прямоугольнике G функция

определена и непрерывна, причём: ,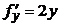

= .

По формуле (10) получим

Метод пикара для решения дифференциального уравнения

Рис. 14

Заметим, что в программе MathCAD для вычисления интегралов с переменным верхним пределом интегрирования, необходимо выполнить следующие действия:

1) записать интеграл и выделить его в рамку;

2) выбрать команду Evaluate (Вычислить) из меню опции Simbolic (Символика) главного меню.

Существует и другой способ вычисления несобственных интегралов в программе MathCAD, по которому следует:

1) записать интеграл и выделить его в рамку;

2) выбрать команду Simplify (Упростить) из меню опции Simbolic (Символика) главного меню.

Пример 2. Найти пять последовательных приближений решения дифференциального уравнения

удовлетворяющего начальному условию у(0) = 0.

Сравнить полученные приближения с точным решением.

Решение.В качестве начального приближения возьмём

Решение данного уравнения, проведённое в системе MathCAD, показано на рис. 15.

Рис. 15

МетодЭйлера

М етод Эйлера относится одновременно к численным и к графическим методам решения дифференциальных уравнений.

Суть метода заключается в том, что искомую интегральную кривую y = y(x) заменяют ломаной M₀M₁M₂ . звенья которой являются касательными к интегральным кривым (рис. 16).

Рис. 16

Пусть требуется решить задачу Коши, т.е. найти решение дифференциального уравнения (1) с начальным условием (2) в виде функции y = y(x). Выбрав шаг h, построим, начиная
с точки х₀, систему равноотстоящих точек:

Вместо искомой интегральной кривойy = y(x) на отрезке [х₀, х₁]рассмотрим отрезок касательной L₁ к ней в точке М₀ (х₀, y₀). Уравнение касательной L₁, в силу (1), имеет вид

При х = х₁ из уравнения касательной L₁ получим

откуда видим, что приращение функции на первом шаге имеет вид

у₀ = hf(х₀, y₀).

Аналогично, проводя касательную L₂ к некоторой интегральной кривой семейства в точке М₁(х₁, y₁), получим

у₁= hf(х₁, y₁).

Таким образом, значения искомой функции y(x) могут быть определены по формулам:

y_i₊₁ =y_i + у _i, у _i = hf(х _i, y_i), (11)

где i= 0,1,2, . , которые называются вычислительными формулами метода Эйлера.

При этом искомую интегральную кривую y = y(x), проходящую через точку М₀ (х₀, y₀), приближённо заменяем так называемой ломаной ЭйлераM₀M₁M₂ . звенья которой M_iM_i₊₁ прямолинейны между прямыми x = x_i, x = x_i₊₁ и имеют подъём

Метод Эйлера является простейшим численным методом, удобным в применении, однако он имеет ряд существенных недостатков. Основной из них — малая точность. Она равна порядку h 2 , причём с каждым шагом погрешность возрастает, т.е. происходит систематическое накопление ошибок. Поэтому на практике часто используют способ двойного счёта — с шагом hи с шагом h/2. Совпадение десятичных знаков в полученных двумя способами результатах даёт естественные основания считать их верными.

Пример.

1. Найти методом Эйлера численное решение дифференциального уравнения
у’ = x 3 + y,удовлетворяющее начальному условию у (0) = 1, на отрезке [0, 1] с шагом h = 0,1.

2. Найти точное решение уравнения у’ = x 3 + y и сравнить его с приближённым на отрезке [0, 1].

1. Для данного уравнения вычислительные формулы (11) имеют вид:

y_i₊₁ =y_i + у _i, у _i = 0,1(х _i 3 + y_i),

Учитывая, что погрешность метода имеет порядок h 2 = 0,01, достаточно в промежуточных результатах брать три цифры после запятой, а во всех y_iсохранять только две цифры.

Результаты вычислений оформим в виде таблицы.

i	х _i	y_i	y_i = hf( х _i , y_i) = 0,1( х _i 3 + y_i)
0	0	1	0,1
1	0,1	1,1	0,110
2	0,2	1,21	0,122
3	0,3	1,33	0,136
4	0,4	1,47	1,634
5	0,5	1,62	0,175
6	0,6	1,79	0,201
7	0,7	1,99	0,233
8	0,8	2,22	0,273
9	0,9	2,49	0,322
10	1	2,82	—

2. Данное уравнение у’ = x 3 + y является линейным дифференциальным уравнением первого порядка. Решим его методом Бернулли.

Полагая y = uv, имеем

= 0.

Сгруппируем члены, содержащие uв первой степени, получим

= 0.

Полагаем = 0, откуда . Интегрируя, находим , или (постоянную интегрирования не вводим, так как достаточно найти какое-либо частное решение этого вспомогательного уравнения).

Для нахождения uимеем уравнение

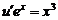
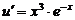
Разделим переменные, получим , откуда

Интегрируем по частям три раза:

Таким образом, общее решение данного уравнения

y = uv = ,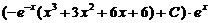

или y = .

Используя начальное условие у (0) = 1, получим 1 = ‑ 6 + С, откуда С = 7. Следовательно, искомое частное (точное) решение имеет вид

у = .

Вычислим значения полученного точного решения на отрезке [0, 1] с шагом h = 0,1. Результаты округлим до 0,01 и запишем в таблицу.

i	х _i	Приближённые значения y_i	Точные значения y (х _i )
0	0	1	1
1	0,1	1,1	1,11
2	0,2	1,21	1,22
3	0,3	1,33	1,35
4	0,4	1,47	1,5
5	0,5	1,62	1,67
6	0,6	1,79	1,86
7	0,7	1,99	2,08
8	0,8	2,22	2,35
9	0,9	2,49	2,66
10	1	2,82	3,03

Сравнение приближённого (численного) решения данного дифференциального уравнения с точным на промежутке [0, 1] проведём с помощью системы MathCAD.

Результаты сравнения, а также численное решение данного уравнения, проведённое методом Эйлера в системе MathCAD, представлены на рис. 17.

Рис. 17

МодификацииметодаЭйлера

Существуют различные уточнения метода Эйлера, повышающие его точность. Цель модификаций — более точно определить направление перехода из точки (х _i, y_i) в точку (х _i ₊₁, y_i ₊₁). Так, метод Эйлера-Коши предлагает вычислять значения искомой функции y(x) по формулам:

= y_i + Ду _i, Ду _i = hf(х _i, y_i),

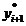
y_i₊₁ = y_i + h ,i= 0,1,2, . .

Геометрически это означает, что мы определяем направление интегральной кривой в исходной точке (х _i, y_i) и во вспомогательной точке (х _i ₊₁, 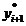). В качестве окончательного берём среднее этих направлений.

Другой модификацией метода Эйлера является усовершенствованный метод ломаных, при котором сначала вычисляют промежуточные значения:

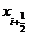
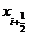
и находят значение направления поля интегральных кривых в средней точке ( , ), т.е. = f( , ), а затем полагают

y_i₊₁ = y_i + h .

Метод Эйлера и его модификации являются простейшими представителями конечно-разностных методов (шаговых методов) для приближённого решения задачи Коши.

Поскольку описанные методы предполагают повторяющиеся вычисления на каждом шаге, то они легко программируются и могут быть реализованы на компьютере.

На рис. 18 и 19 показаны решения дифференциального уравнения у’ = x 3 + y,удовлетворяющего начальному условию у(0) = 1, полученные модифицированными методами Эйлера (методом Эйлера-Коши и усовершенствованным методом ломаных) с помощью системы MathCAD.

Рис. 18

Рис. 19

Метод Рунге-Кутта

Рассмотренный выше метод Эйлера относится к семейству методов Рунге-Кутта и является их простейшим частным случаем (методом первого порядка точности). Наиболее известным из методов Рунге-Кутта является классический четырёхэтапный метод четвёртого порядка точности. Его расчётные формулы для решения задачи Коши, определённой уравнениями (1) и (2), имеют вид:

y_i₊₁ =y_i + у _i; у _i= ( k₁ (i) + 2k₂ (i) + 2k₃ (i) + k₄ (i) ), (12)

k₂ (i) = h f (х _i + ,y_i + );

k₃ (i) = h f (х _i + , y_i + );

Погрешность метода на каждом шаге является величиной порядка h 5 .

Геометрический смысл использования метода Рунге-Кутта с вычислительными формулами (12) состоит в следующем (рис. 20).

Рис. 20

Из начальной точки М₀(х₀, y₀) сдвигаются в направлении, определяемом углом ₁, для которого tg ₁= f (х₀, y₀). Идут в этом направлении на полшага, т.е. до вертикальной прямой
х = х₀ + . На этом направлении выбирается точка Р₁с координатами

Затем из точки М₀(х₀, y₀)сдвигаются в направлении, определяемом углом ₂, для которого tg ₂ = f (х₀ + ,y₀ + ), и на этом направлении выбирается точка Р₂с координатами

Далее из точки М₀(х₀, y₀) сдвигаются в направлении, определяемом углом ₃, для которого tg ₃ = f . На этом направлении выбирается точка Р₃с координатами

(х₀ + h, y₀ + k₃ (0) ). Этим задаётся ещё одно направление, определяемое углом ₄, для которого tg ₄ = = f(х₀ + h, y₀ + k₃ (0) ). Четыре полученных направления усредняются в соответствии с формулой

= (k₁ (0) +2k₂ (0) + 2k₃ (0) + k₄ (0) ).

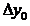
На этом окончательном направлении и выбирается очередная точка М₁с координатами (х₁, y₁) = (х₀+ h, y₀ + ).

Теперь, уже исходя из точки М₁, все построения с помощью усреднений направлений повторяют сначала. Идут в новом усреднённом направлении до вертикальной прямой х = х₂, получают точку М₂(х₂, y₂) и т.д.

Эффективная оценка метода Рунге-Кутта затруднительна [2, 4]. Поэтому для определения правильности выбора шага h на практике обычно на каждом этапе из двух шагов применяют двойной пересчёт, а именно: исходя из текущего верного значения y(х _i) вычисляют величину y(х _i+ 2h) двумя способами: один раз с шагом h, другой раз — с двойным шагом 2h .

Если расхождение полученных значений не превышает допустимой погрешности, то шаг hдля данного этапа выбран правильно и полученное с его помощью значение можно принять за y (х _i+ 2h). В противном случае шаг уменьшают в два раза.

На практике при вычислениях по формулам (15) обычно пользуются схемой, приведённой в таблице.

i	x	Y	k = hf (х, y )	у
0	х ₀ х₀ + х₀ + х₀ + h	y ₀ y₀ + y₀ + y₀ + k₃ (0)	k₁ (0) k₂ (0) k₃ (0) k₄ (0)	k₁ (0) 2k₂ (0) 2k₃ (0) k₄ (0)
—	—	—	—
1	х₁	y₁	. . .	. . .

Пример. Найти методом Рунге-Кутта решение дифференциального уравнения у’ = x 3 + y,удовлетворяющего начальному условию у(0) = 1, на отрезке [0, 1] с шагом h = 0,1.

Решение.Учитывая, что погрешность метода имеет порядок h 5 = 0,00001, в промежуточных результатах следует брать пять цифр после запятой, а во всех y_iсохранять только четыре цифры. Результаты вычислений оформим в виде таблицы.

i	х	y	k = 0,1(х 3 + y )	y
0	0 0,05 0,05 0,1	1 1,05 1,0525 1,1053	0,1 1,10501 1,10526 1,11063	0,1 0,21003 0,21053 0,11063
0,1052
1	0,1 0,15 0,15 0,2	1,1052 1,1604 1,1634 1,2219	0,11062 0,11637 0,11668 0,11136	0,11062 0,23278 0,21121 0,11136
0,10556
2	0,2 0,25 0,25 0,3	1,2218 1,2717 1,2752 1,3399	0,12188 0,12874 0,12908 0,13669	0,12188 0,25747 0,25816 0,13669
0,12903
3	0,3 0,35 0,35 0,4	1,3520 1,4081 1,4124 1,4853	0,13668 0,1451 0,14552 0,15493	0,13668 0,2902 0,29105 0,15493
0,14548
4	0,4 0,45 0,45 0,5	1,4988 1,5628 1,568 1,6512	0,15493 0,16539 0,16591 0,17762	0,15493 0,33078 0,33182 0,17762
0,16586
5	0,5 0,55 0,55 0,6	1,6661 1,74 1,7465 1,8425	0,17762 0,19064 0,19132 0,20585	0,17762 0,38128 0,38258 0,20585
0,19122
6	0,6 0,65 0,65 0,7	1,8588 1,9618 1,9699 2,0826	0,20584 0,22199 0,2228 0,24082	0,20584 0,44399 0,4456 0,24082
0,22271
7	0,7 0,75 0,75 0,8	2,0833 2,1855 2,1955 2,3268	0,24081 0,26074 0,26173 0,28388	0,24081 0,52148 0,52347 0,28388
0,26161
8	0,8 0,85 0,85 0,9	2,3468 2,4898 2,5021 2,6585	0,28589 0,3104 0,31162 0,33875	0,28589 0,62079 0,62324 0,33875
0,31145
9	0,9 0,95 0,95 1	2,6582 2,8545 2,8695 3,0566	0,34129 0,37119 0,37269 0,40566	0,34129 0,74238 0,74537 0,40566
0,37245
10	1	3,0280

Соответствующее решение данного дифференциального уравнения, полученное методом Рунге-Кутта в системе MathCAD, представлено на рис. 21.

Рис. 21

Лабораторная работа

«Численные методы решения задачи Коши
для обыкновенных дифференциальных уравнений»

Задание 1.

1. Для заданного дифференциального уравнения первого порядка у’ = f(x , y) c начальным условием у (a) = c найти приближённое решение в виде многочлена пятой степени.

2. Найти численное решение данного дифференциального уравнения на отрезке [a, b] с шагом интегрирования h, округляя результат до 0,001.

3. Найти точное решение заданного дифференциального уравнения у’ = f (x, y) и сравнить его с приближённым на отрезке [a, b]. Построить графики полученных решений.

Исходные данные для 15-ти вариантов содержатся в таблице.

Вариант	f ( x , y )	a	b	с	h
1		0	1	0	0,1
2		0	1	1	0,1
3		0	2	0	0,1
4		p	2p	0	p/10
5		1	2		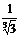0,1
6		1	3		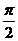0,2
7	4 +	1	2	2	0,1
8		1	2	0	0,2
9		0	2	0	0,1
10		0	2	1	0,2
11		1	2	0	0,2
12	–	0	1	p/4	0,1
13	–			е	0,1
14		0	1	1	0,1
15				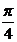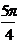0	0,3

Указания к выполнению задания 1

1. Для того, чтобы получить приближённое решение заданного дифференциального уравнения в виде многочлена пятой степени, используйте формулу (3) при k = 0, 1, . 5.

2. При выборе метода для вычисления точного решения учитывайте то, что дифференциальные уравнения вариантов 1- 4 являются линейными дифференциальными уравнениями, уравнение 5-го варианта — уравнение Бернулли, уравнения 6-8-х вариантов — однородные дифференциальные уравнения, а уравнения 9-15-х го вариантов — дифференциальные уравнения с разделяющимися переменными.

3. Для сравнения точного и приближённого решений заданного дифференциального уравнения сначала составьте таблицы их значений на отрезке [a , b], затем постройте на этом же отрезке графики полученных решений.

Задание 2. Решить задачу Коши для обыкновенного дифференциального уравнения первого порядка у’ = f(x , y) на отрезке [a , b]при заданном начальном условии у(a) = c и шаге интегрирования h:

1) методом Эйлера с шагом 2h и с шагомh;

2) модифицированным методом Эйлера (методом Эйлера — Коши или усовершенствованным методом ломаных);

3) методом Рунге-Кутта с шагом 2h и с шагомh.

Результаты округлить до 0,0001. Сравнить полученные разными методами решения. Построить графики полученных решений.

Видео:Метод Пикара последовательных приближений для решения дифференциальных уравненийСкачать

Метод пикара для решения дифференциального уравнения

4. Численные методы решения дифференциальных уравнений.

Численные методы решения ОДУ.

Если неизвестная функция, входящая в д.у. зависит от одной независимой переменной, то такое д.у. обычное.

Порядок д.у. – наивысший порядок производной, входящей в это уравнение.

Д.у. n -ого порядка – уравнение вида 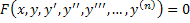, где x – независимая переменная, y – неизвестная функция.

Решение или интеграл д.у. — всякая дифференцируемая n -раз функция y = f ( x ), обращающая д.у. n -ого порядка в тождество.

График решения – интегральная кривая.

Общее решения д.у. y = f ( x ) – 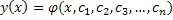, c – порядок уравнения.

Частное решение д.у. – такое решение, которое может быть получено из общего при определенных числовых значений постоянного интегрирования, входящих в общее решение.

Задача Коши (начальная задача) – нахождение частного решения д.у. n -ого порядка, удовлетворяющего n начальным условиям.

при n =1 начальное условие

Теорема Коши: если f ( x , y ) непрерывна в замкнутой области D ( x , y )и имеет ограниченную частную производную по y

то для любого x , y из D существует единственное решение y ( x ) ОДУ первого порядка.

Метод последовательных приближений Пикара.

Метод позволяет получить приближенное решение д.у. y ’= f ( x , y ).

Рассмотрим случай с начальным условием

Проинтегрируем обе части от x 0 до x (3)

при 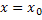получаем

Суть метода Пикара – использование интегрального уравнения (3) для построения интерактивного алгоритма решения задачи Коши.

Численные решения ОДУ. Методы Эйлера.

Универсальный численный метод решения д.у. – метод конечных разностей. Сущность – замена области непрерывного измерения аргумента дискретным множеством точек (сеткой или сеточной области с постоянным или переменным шагом h ).

Много общего с методом Эйлера – последовательные значения y ₁ искомой функции y определяются по формуле

Если разложить функцию в ряд Тейлора и ограничится членами до h 4 , то приращение функции (2):

где производные y ’( x ), y ’’( x ), y ’’( x ), y ’ v ( x ) определятся последовательным дифференцированием из уравнения y ’= f ( x )

Вместо непосредственных вычислений по формуле (2) в методе Рунге-Кутта определяются 4 числа:

Многошаговые методы. Решение в текущем узле зависит от данных в нескольких предыдущих узлах.

Вычисление таблицы приближённых значений решения в начальных точках.

Пусть требуется найти приближенное решение дифференциального уравнения y‘ = f(x,y) , удовлетворяющее начальному условию y(x₀) = y₀ . Численное решение задачи состоит в построении приближенного значения y₁ решения уравнения y(x) в точке x₁ = x₀ + h . Методами Адамса называют группу многошаговых методов, в которых приближенное решение y_n _{+ 1} = y(x_n _{+ 1}) в точке x_n _{+ 1} = x₀ + h(n + 1) вычисляется по формуле, использующей полином P(x) наименьшей степени, интерполирующий правую часть f(x,y) по значениям f_n,f_n _{− 1}. f_n _{− k + 1},f_r = f(x_r,y_r) . Методы, в которых P(x) = P_kn(x) называют k -шаговыми явными методами Адамса — Башфорта, а методы, в которых P(x) = P_k _{+ 1n + 1} — (k + 1) -шаговыми неявными методами Адамса — Мултона. Методы Адамса k -го порядка требуют предварительного вычисления решения в k начальных точках. Часто для вычисления дополнительных начальных значений используется 4-стадийный метод Рунге — Кутта 4-го порядка точности.