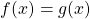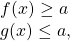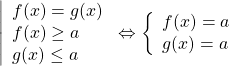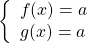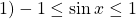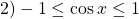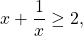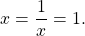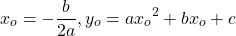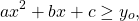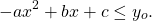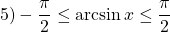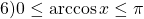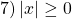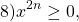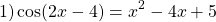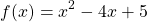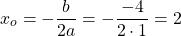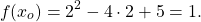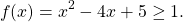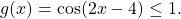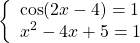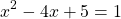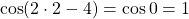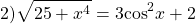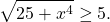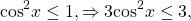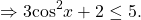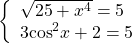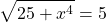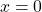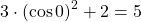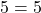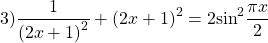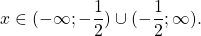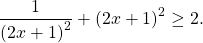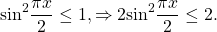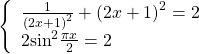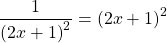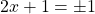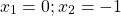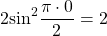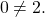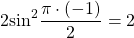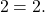Метод оценки уравнений в тригонометрии

Решение уравнений методом оценки основано на сравнении области значений функций, стоящих в левой и правой части уравнения.

Если в уравнении

то равенство возможно тогда и только тогда, когда и f(x) и g(x) одновременно равны a:

При этом, если максимальное значение функции, стоящей в одной части уравнения, равно минимальному значению функции, стоящему в другой части уравнения, и эти значения достигаются для обеих функций при x=x0, то xo — корень уравнения.

Графически это можно проиллюстрировать так:

Если максимальное значение функции, стоящей в одной части уравнения, равно минимальному значению функции, стоящему в другой части уравнения, но эти значения достигаются при разных x0, то уравнение не имеет корней:

Получив систему уравнений

достаточно решить одно из уравнений (которое проще), а затем проверить, являются ли найденные корни корнями другого уравнения.

Чаще всего при решении уравнений методом оценки правой и левой части используют следующие соображения:

причём равенство достигается при

4) Квадратичная функция в вершине параболы (x0; y0)

при a>0 принимает своё наименьшее значение:

при отрицательном коэффициенте a при x² — наибольшее значение:

где n — натуральное число.

Примеры решения уравнений методом оценки левой и правой части.

— квадратичная функция. График — парабола ветвями вверх. Наименьшее значение принимает в вершине

С другой стороны

Следовательно, исходное уравнение равносильно системе уравнений

Корень второго уравнения:

x=2. Проверяем, является ли 2 корнем первого уравнения:

— верно. Следовательно, x=2 — единственный корень.

Так как x⁴≥0, то 25+ x⁴≥25, а значит,

С другой стороны,

Следовательно, исходное уравнение равносильно системе уравнений

Решаем первое уравнение

Проверяем, является ли x=0 корнем второго уравнения:

— верно. Значит, x=0 — корень данного уравнения.

Так как сумма взаимно-обратных положительных чисел не меньше двух,

Так как сумма положительных взаимно-обратных чисел равна 2, если эти числа равны между собой, то

Проверяем, являются ли эти корни корнями второго уравнения.

Таким образом, исходное уравнение имеет единственный корень x= -1.

Видео:10 класс, 23 урок, Методы решения тригонометрических уравненийСкачать

Алгебра и начала математического анализа. 10 класс

Конспект урока

Алгебра и начала математического анализа, 10 класс

Урок №47. Методы решения тригонометрических уравнений.

Перечень вопросов, рассматриваемых в теме:

• Формирование системы знаний и умений решать тригонометрические уравнения различными методами;
• Применение метода разложения на множители при решении тригонометрических уравнений;
• Применение метода оценки при решении тригонометрических уравнений;
• Прием домножения левой и правой частей уравнения на тригонометрическую функцию при решении тригонометрических уравнений.

Глоссарий по теме

Теорема — основа метода разложения на множители

Уравнение равносильно на своей области определения совокупности .

Теорема — основа метода замены переменной

Уравнение равносильно на ОДЗ совокупности уравнений

.

Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е., Шабунин М.И. под ред. Жижченко А.Б. Алгебра и начала математического анализа. 10 класс: учеб. для общеобразоват. учреждений: базовый и профил. Уровни – 2-е изд. – М.: Просвещение, 2011. – 368 с.: ил. – ISBN 978-5-09-025401-4, сс.327-332

Шахмейстер А.Х. Тригонометрия. М.: Издательство МЦНМО : СПб.: «Петроглиф» : «Виктория плюс», 2013. – 752 с.: илл. ISBN 978-5-4439-0050-6, сс.219-221, 245-262

Открытые электронные ресурсы:

Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/

Теоретический материал для самостоятельного изучения

На этом уроке мы продолжаем заниматься решением тригонометрических уравнений. И здесь мы рассмотрим такие методы как разложение на множители, метод оценки, а также продолжим решать тригонометрические уравнения методом замены переменной. Кроме того, мы узнаем, как использовать домножение правой и левой частей уравнений для получения более простого уравнения, как использовать тригонометрические формулы для решения уравнений.

Сейчас выполните несколько заданий.

Представьте в виде произведения:

Используем формулы приведения, затем формулу преобразования суммы косинусов в произведение:

.

(На последнем шаге мы фактически использовали формулу двойного аргумента:

.

Ответ: .

Воспользуемся формулой понижения степени и формулой преобразования произведения косинусов в сумму косинусов. Появившийся при этом общий множитель вынесем за скобки:

Воспользуемся тем, что косинус – функция четная и известным значением косинуса. В результате получим:

При выполнении этого задания будем использовать прием домножения о деления левой части на одно и то же тригонометрическое выражение.

Но сначала заметим, что .

Теперь запишем левую часть: .

теперь домножим и разделим это выражение на : .

Теперь воспользуемся формулой синуса двойного аргумента и получим:

. Теперь еще раз воспользуемся формулой двойного аргумента, предварительно домножив числитель и знаменатель на 2:

Учитывая, что , получаем: .

То есть исходное равенство верно.

Объяснение новой темы

1. Рассмотрим метод разложения на множители

Теоретической основой метода разложения на множители является теорема:

Уравнение равносильно на своей области определения совокупности .

Для того чтобы применить эту теоремы, нужно исходное уравнение привести к виду , используя разные приемы.

Решить уравнение:

Перенесем правую часть уравнения в левую и преобразуем:

, .

Ответ: .

В этом случае мы использовали метод группировки для разложения на множители тригонометрического выражения.

Часто для преобразования выражения в произведение нужно использовать тригонометрические формулы. Рассмотрим такой пример:

Решить уравнение:

Преобразуем разность синусов в произведение:

Теперь вынесем за скобку общий множитель:

И решим каждое из двух уравнений: .

. Заметим, что вторая серия решений включается в первую. Поэтому мы можем оставить в ответе только первую серию.

Ответ: .

2. Замена переменной

Еще один метод решения тригонометрических уравнений — это метод разложения на множители. Мы уже знакомились с ним, когда решали уравнения, сводимые к квадратному или другому алгебраическому уравнению, когда решали однородные уравнения, а также знакомились с универсальной тригонометрической подстановкой. На этом уроке мы познакомимся еще с одной заменой, которая позволяет решать тригонометрические уравнения.

Рассмотрим уравнение вида:

или .

Для его решения введем новую переменную .

Тогда .

Выразим отсюда (или ).

Решите уравнение

Сделаем замену . Тогда .

Вспомогательное уравнение имеет вид:

.

.

Вернемся к исходной переменной:

.

Решим каждое из этих уравнений с помощью формулы введения вспомогательного угла:

, .

Так как , то оба уравнения имеют решения:

, .

Ответ: .

3. Теперь рассмотрим метод оценки

Часто этот метод применяют в том случае, когда уравнение включает в себя функции разного типа, например, тригонометрические и показательные, и обычные преобразования на приводят к результату. Но мы рассмотрим метод оценки при решении тригонометрических уравнений. Он основан на свойстве ограниченности тригонометрических выражений.

Решить уравнение: .

Мы знаем, что . С другой стороны, для того чтобы произведение двух различных чисел было равно 1, то они должны быть взаимно обратными, то есть если одно из них меньше 1,то другое больше 1. Но так как косинус больше 1 быть не может, то равенство может выполняться только в двух случаях:

или .

или .

или .

Вторая система ни при каких значениях k и n не имеет решений.

Первая система имеет решения при n=3m, k=2m, поэтому ее решения, а значит, и решение уравнения:

Ответ:

Рассмотрим еще один пример, в котором метод оценки применяется для решения уравнения, правая и левая части которого являются функциями разного типа.

Рассмотрим левую часть уравнения и преобразуем его:

.

Поэтому

Теперь рассмотрим правую часть: .

Поэтому данное уравнение решений не имеет.

Ответ: решений нет

Рассмотрим несколько задач.

Домножим уравнение на 2 и воспользуемся формулой понижения степени:

Теперь воспользуемся формулой преобразования суммы косинусов с произведение:

.

Теперь перенесем правую часть в левую и вынесем за скобку общий множитель:

Теперь используем формулу преобразования разности косинусов в произведение:

Теперь решим три простейших тригонометрических уравнения:

, .

В этом случае достаточно оставить первые две серии решений, так как числа вида при нечетных значениях m попадают в первую серию решений, а при четных — во вторую.

Таким образом, получаем ответ:

Ответ:

Используя метод вспомогательного угла, оценим выражение, стоящее в левой части уравнения.

То есть будем рассматривать левую часть уравнения как выражение вида:

, где .

Мы знаем, что , поэтому

Поэтому уравнение решений не имеет.

Ответ: решений нет.

Рассмотрим решение более сложного уравнения методом оценки.

Запишем уравнение в виде

Преобразуем левую часть:

Так как , то

и .

Так как и , то

Равенство возможно только при одновременном выполнении условий:

.

,

.

.

, .

Решая эту систему, получим, что, .

Ответ: , .

Рассмотрим еще один прием, который применяется при решении тригонометрических уравнений.

Домножение левой и правой части на тригонометрическую функцию

Рассмотрим решение уравнения:

Домножим обе части уравнения на :

.

Заметим, что домножая обе части уравнения на выражение с переменной, мы можем получить новые корни. Проверим те значения переменной, при которой :

не являются решением исходного уравнения, поэтому мы должны будем удалить эти числа из полученного решения.

Теперь с помощью формулы синуса двойного аргумента преобразуем полученное уравнение:

Теперь перенесем правую часть в левую и преобразуем по формуле преобразования разности синусов в произведение:

, .

Учитывая, что , получим: .

Ответ: .

Примеры и разборы решений заданий тренировочного модуля

Ответ:

Решите уравнение. Найдите коэффициенты a, b, c

Ответ:

Представим левую и правую части уравнения в виде произведения. Затем перенесём всё в левую часть и разложим на множители

Ответ:

Видео:"Олимпиадная" тригонометрия. Метод оценокСкачать

Метод оценки уравнений в тригонометрии

Видео:№12 из ЕГЭ 2022 по профильной математике. Метод оценки - ИМБАСкачать

Методы решения тригонометрических уравнений.

Видео:3,5 способа отбора корней в тригонометрии | ЕГЭ по математике | Эйджей из ВебиумаСкачать

1. Алгебраический метод.

( метод замены переменной и подстановки ).

Видео:Сложная тригонометрия на вспомогательный угол и оценку (Ткачук)Скачать

2. Разложение на множители.

П р и м е р 1. Решить уравнение: sin x + cos x = 1 .

Р е ш е н и е . Перенесём все члены уравнения влево:

sin x + cos x – 1 = 0 ,

преобразуем и разложим на множители выражение в

левой части уравнения:

П р и м е р 2. Решить уравнение: cos 2 x + sin x · cos x = 1.

Р е ш е н и е . cos 2 x + sin x · cos x – sin 2 x – cos 2 x = 0 ,

sin x · cos x – sin 2 x = 0 ,

sin x · ( cos x – sin x ) = 0 ,

П р и м е р 3. Решить уравнение: cos 2 x – cos 8 x + cos 6 x = 1.

Р е ш е н и е . cos 2 x + cos 6 x = 1 + cos 8 x ,

2 cos 4x cos 2x = 2 cos ² 4x ,

cos 4x · ( cos 2x – cos 4x ) = 0 ,

cos 4x · 2 sin 3x · sin x = 0 ,

1). cos 4x = 0 , 2). sin 3x = 0 , 3). sin x = 0 ,

Видео:Тригонометрия в ЕГЭ может быть простойСкачать

3. Приведение к однородному уравнению.

а) перенести все его члены в левую часть;

б) вынести все общие множители за скобки;

в) приравнять все множители и скобки нулю;

г ) скобки, приравненные нулю, дают однородное уравнение меньшей степени, которое следует разделить на

cos ( или sin ) в старшей степени;

д) решить полученное алгебраическое уравнение относительно tan .

П р и м е р . Решить уравнение: 3 sin 2 x + 4 sin x · cos x + 5 cos 2 x = 2.

Р е ш е н и е . 3sin 2 x + 4 sin x · cos x + 5 cos 2 x = 2sin 2 x + 2cos 2 x ,

sin 2 x + 4 sin x · cos x + 3 cos 2 x = 0 ,

tan 2 x + 4 tan x + 3 = 0 , отсюда y 2 + 4y +3 = 0 ,

корни этого уравнения: y ₁ = — 1, y ₂ = — 3, отсюда

1) tan x = –1, 2) tan x = –3,

Видео:Щелчок по математике I №5,6,12 Тригонометрия с нуля и до ЕГЭ за 4 часаСкачать

4. Переход к половинному углу.

П р и м е р . Решить уравнение: 3 sin x – 5 cos x = 7.

Р е ш е н и е . 6 sin ( x / 2 ) · cos ( x / 2 ) – 5 cos ² ( x / 2 ) + 5 sin ² ( x / 2 ) =

= 7 sin ² ( x / 2 ) + 7 cos ² ( x / 2 ) ,

2 sin ² ( x / 2 ) – 6 sin ( x / 2 ) · cos ( x / 2 ) + 12 cos ² ( x / 2 ) = 0 ,

tan ² ( x / 2 ) – 3 tan ( x / 2 ) + 6 = 0 ,

Видео:Тригонометрические уравнения. ЕГЭ № 12 | Математика | TutorOnline tutor onlineСкачать

5. Введение вспомогательного угла.

где a , b , c – коэффициенты; x – неизвестное.

Теперь коэффициенты уравнения обладают свойствами синуса и косинуса , а именно : модуль ( абсолютное значение ) каждого из них не больше 1, а сумма их квадратов равна 1 . Тогда можно обозначить их соответственно как cos и sin ( здесь — так называемый вспомогательный угол ), и наше уравнение прини мает вид:

Видео:Профильный ЕГЭ 2024. Задача 12. Тригонометрические уравнения. 10 классСкачать

6. Преобразование произведения в сумму.

П р и м е р . Решить уравнение: 2 sin x · sin 3 x = cos 4 x .

Р е ш е н и е . Преобразуем левую часть в сумму:

💡 Видео

Тригонометрические уравнения | Борис ТрушинСкачать

Простейшие тригонометрические уравнения. y=sinx. 1 часть. 10 класс.Скачать

Как решить пункт б) в задании 13 профиля ЕГЭ. ТригонометрияСкачать

Решение тригонометрических уравнений. Однородные уравнения. 10 класс.Скачать

СЕКРЕТНЫЙ ЛАЙФХАК С ТРИГОНОМЕТРИЕЙ НА ЕГЭ #shorts #математика #егэ #огэ #тригонометрияСкачать

ГРОБ в №13 на ЕГЭ 2021 по математике. Метод вспомогательного угла. Тригонометрия и ФСУСкачать

Алгебра 10 класс (Урок№47 - Методы решения тригонометрических уравнений.)Скачать

А ты знаешь, когда в тригонометрических уравнениях писать пk, а когда 2пk? #математика #егэ2023 #егэСкачать

Решение тригонометрических уравнений. 10 класс.Скачать

Решаем тригонометрические уравнения через разложение на множители или деление на косинус вСкачать