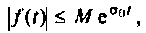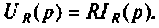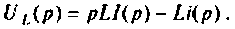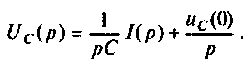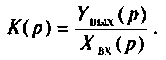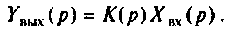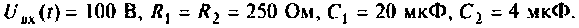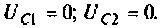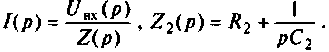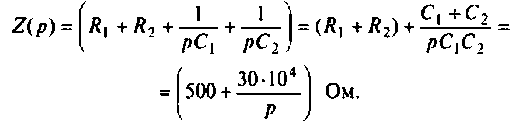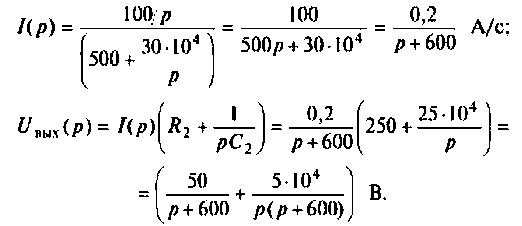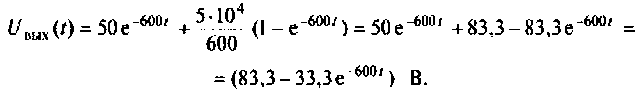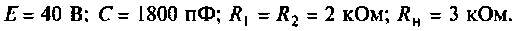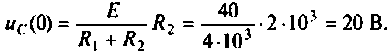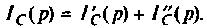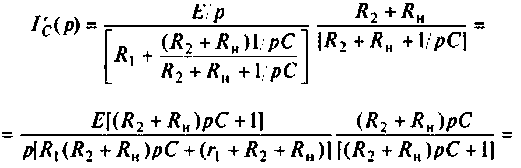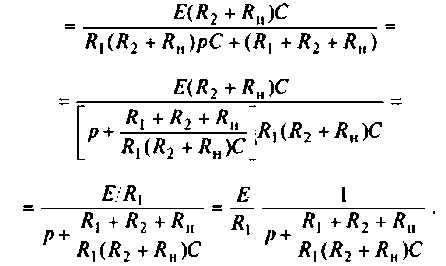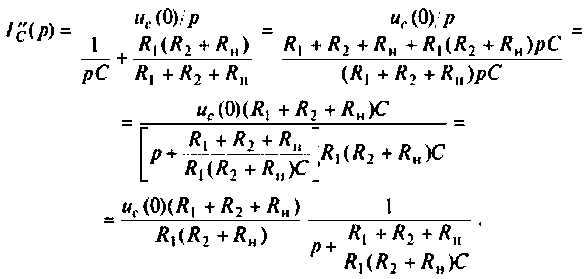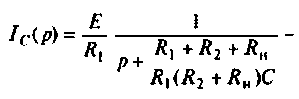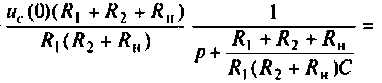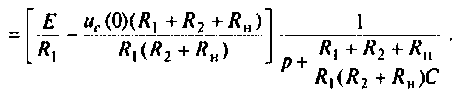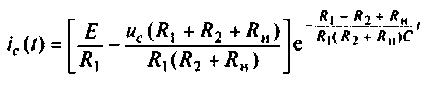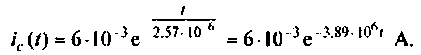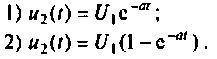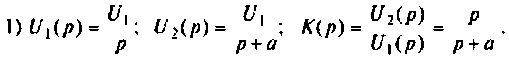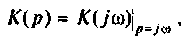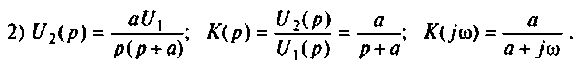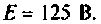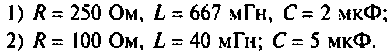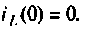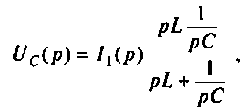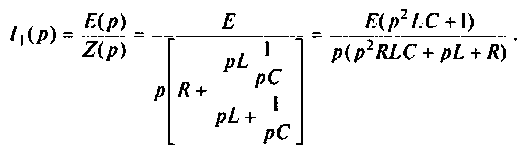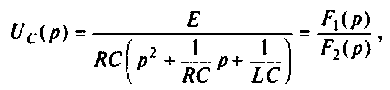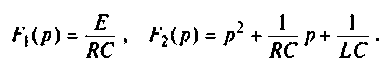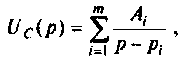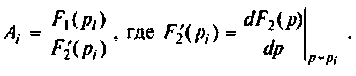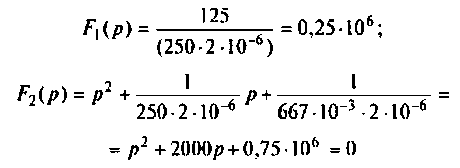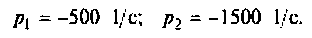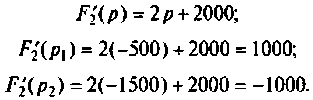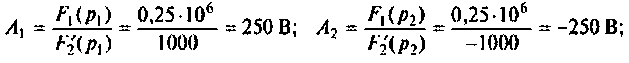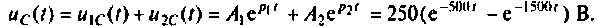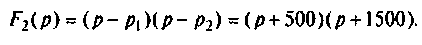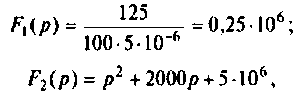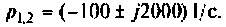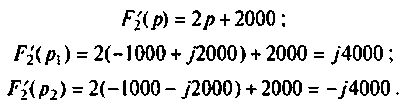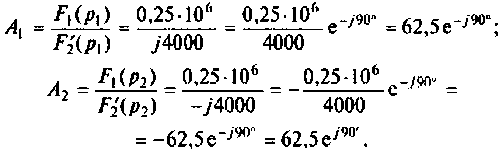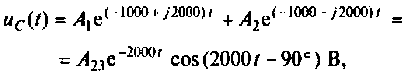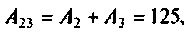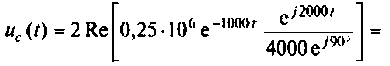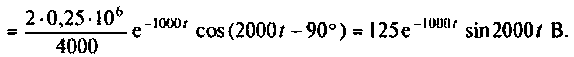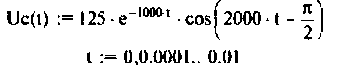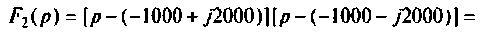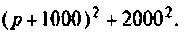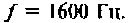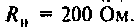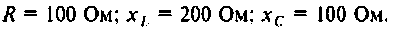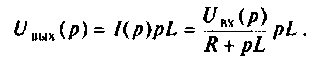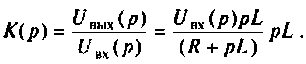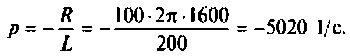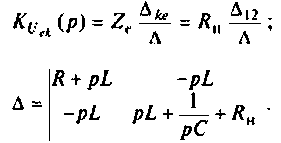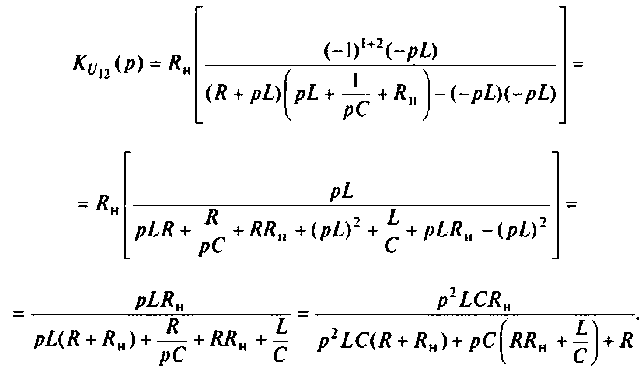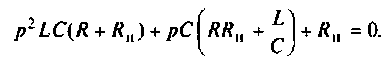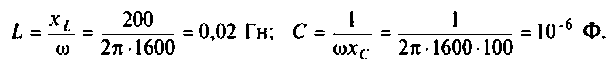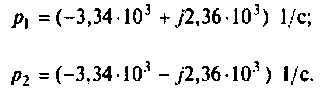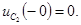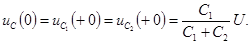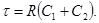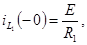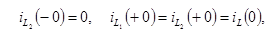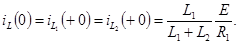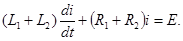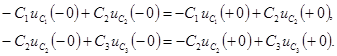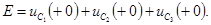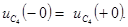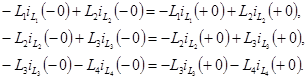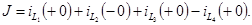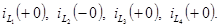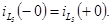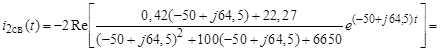Содержание:
Операторный метод расчета переходных процессов:
Для решения линейных дифференциальных и интегродифференциальных уравнений в теории электрических цепей нашел широкое применение так называемый операторный метод, основанный на преобразованиях Лапласа.
Сущность этого метода заключается в том что функции вещественного переменного t преобразуются в функции комплексного переменного
Переход от функции вещественного переменного t к функции комплексного переменного p осуществляется с помощью прямого преобразования Лапласа
Обратный переход от функции комплексного переменного р к функциям вещественного переменного t осуществляется на основании обратного преобразования Лапласа
Функцию 
Напомним, что для того чтобы функция 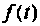
- удовлетворяла условиям Дирихле;
- была равна нулю для отрицательных значений t, т. е. при
- в интервале
не возрастала быстрее, чем некоторая показательная функция
где 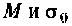
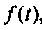
Применение свойств преобразования Лапласа в сочетании с теоремой разложения дает возможность составить таблицы изображений и оригиналов, облетающие и ускоряющие нахождение оригиналов по изображениям [4, 26]. Применение операторного метода совместно с компьютерными математическими программными средами делает анализ и расчет электрических цепей доступным, быстрым и интересным.
Особенностью метода является необходимость выполнения трех этапов:
- Эквивалентные операторные схемы замещения элементов
- Операторные функции электрических цепей
- Анализ переходных процессов в цепях с помощью операторных функций
- Примеры решения задач
- V. Особенности расчета переходных процессов в цепях с емкостными контурами и индуктивными сечениями
- II. ОПЕРАТОРНЫЙ МЕТОД РАСЧЕТА
- 🎥 Видео
Видео:Переходные процессы | Классический метод расчета переходных процессов. Теория и задачаСкачать

Эквивалентные операторные схемы замещения элементов
Активное сопротивление:
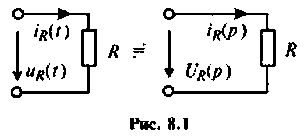
На рис. 8.1 изображена схема замещения в операторном виде участка цепи с активным сопротивлением. Для этого участка цепи связь между операторным напряжением и током записывается в виде
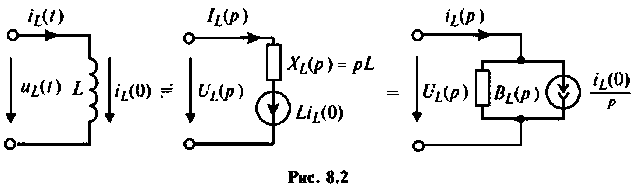
Индуктивность:
Для участка цепи с индуктивностью при ненулевых начальных условиях операторная схема замещения изображена на рис. 8.2.
Связь между операторным напряжением и током записывается в виде
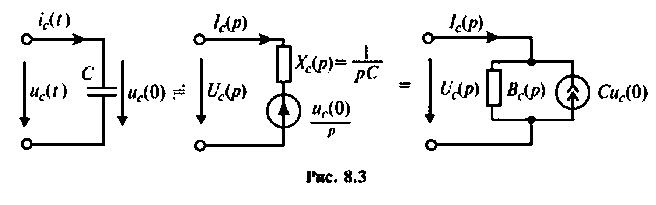
Емкость:
Для участка цепи с емкостью при ненулевых начальных условиях операторная схема замещения изображена на рис. 8.3.
Связь между напряжением и током устанавливает соотношение
В эквивалентных операторных схемах для индуктивности и емкости с ненулевыми начальными условиями возникают дополнительные источники ЭДС 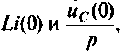
Порядок расчета:
- определяют независимые начальные условия;
- составляют эквивалентную операторную схему замещения для послекоммутационной цепи;
- составляют систему уравнений в операторной форме в соответствии с выбранным рациональным методом расчета эквивалентной схемы замещения и решают ее относительно изображений неизвестных величин;
- для нахождения оригиналов неизвестных величин используют таблицы соответствия, формулы теоремы разложения, компьютерные программные среды и др.
Операторные функции электрических цепей
Основные операторные функции:
Операторной функцией цепи называется отношение изображения по Лапласу выходной величины 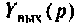
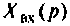
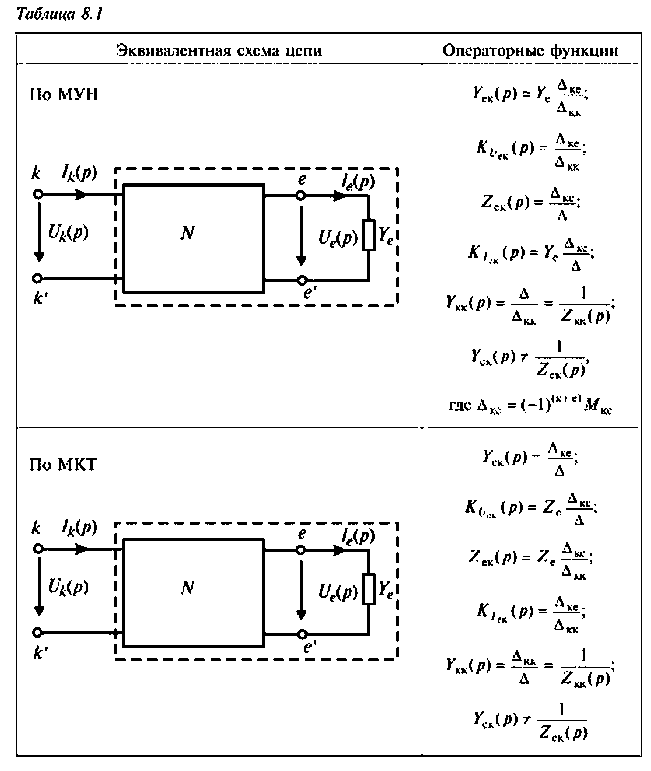
Операторная функция зависит только от параметров цепи и ее схемы. Различают входные и передаточные операторные функции. В табл. 8.1 приведены соотношения для расчета операторных функций сложных цепей.
Для расчета операторных функции можно применять все методы расчета комплексных функций
т. е. комплексная функция является частным случаем операторной при замене оператора 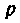
Анализ переходных процессов в цепях с помощью операторных функций
По известной операторной функции цепи и операторному изображению воздействия можно найти реакцию цепи на это воздействие
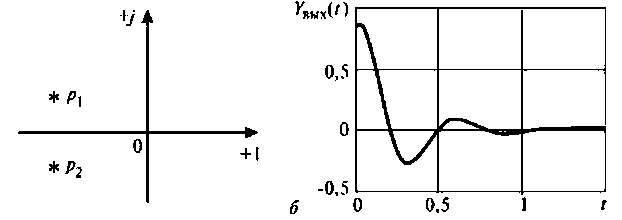
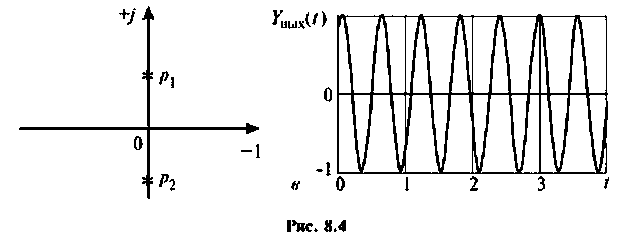
На рис. 8.4 (а—в) приведены временные диаграммы переходных процессов, а также полюсно-нулевое представление на комплексной плоскости.
По расположению полюсов операторной функции можно судить о характере переходное процесса:
- если все полюсы расположены только на отрицательной вещественной полуоси, то переходный процесс в цепи носит апериодический характер;
- если имеются сопряженные полюсы в левой полуплоскости, то переходный процесс носит характер затухающих колебаний;
- если все полюсы расположены только на отрицательной мнимой оси, то переходный процесс в цепи носит характер незатухающих колебаний.
Примеры решения задач
Пример 8.4.1.
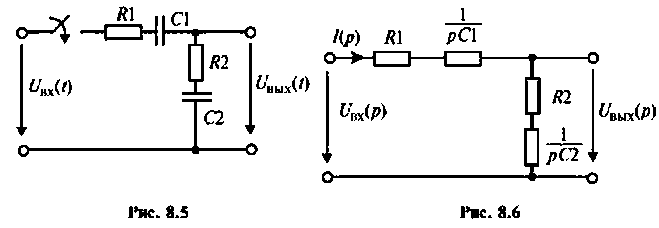
В интегродифференцирующем контуре постоянного тока (рис. 8.5), применяемом для коррекции ЭЦ и САУ. определить напряжение 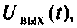
Решение
Определяют независимые начальные условия — напряжения на емкостях. До коммутации ключ был разомкнут, напряжение на емкостях отсутствовало:
Изображают эквивалентную операторную схему замещения после коммутации (рис. 8.6).
Находят изображение напряжения 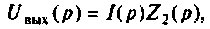
Сопротивление всей цепи определяется выражением
По данному изображению находят оригинал (рис. 8.7) напряжения 
Пример 8.4.2.
К пассивному RС-фильтру нижних частот подключается нагрузка 
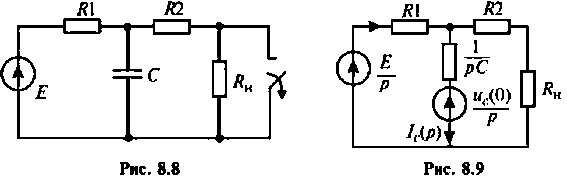
Дано:
Решение
Определяют независимые начальные условия — напряжение на емкости
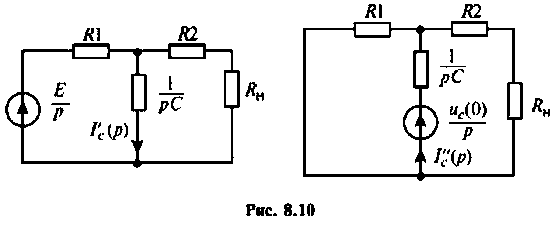
Изображают эквивалентную операторную схему замещения после коммутации (рис. 8.9).
Операторный ток 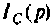
Операторные схемы, соответствующие частичным токам, изображены на рис. 8.10.
Искомый ток
Определяют частичный ток
Аналогично определяют частичный ток
По данному изображению 
Подставляя числовые значения величин, получают
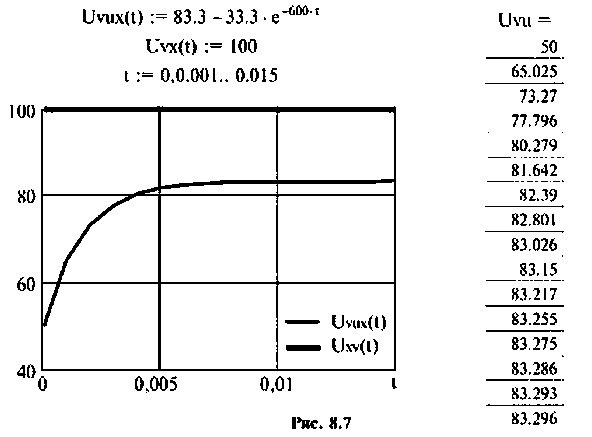
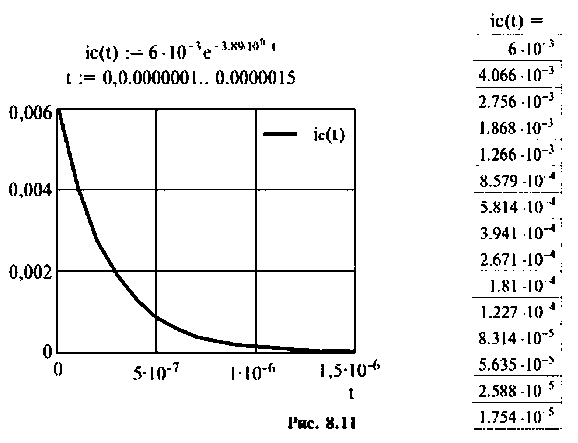
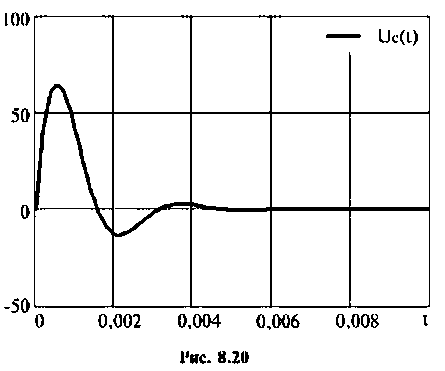
Строят график тока 
Выводы. До коммутации напряжение на емкости определялось падением напряжения на сопротивлении 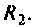
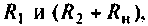
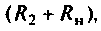
Пример 8.4.3.
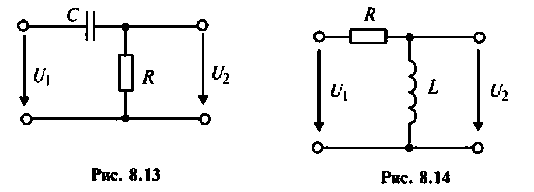
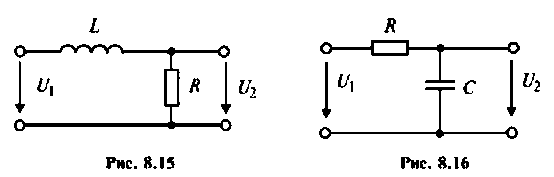
Рассчитать коэффициент передачи по напряжению пассивной цепи (рис. 8.12) и составить ее схему так, чтобы при подключении на вход источника постоянной ЭДС 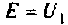
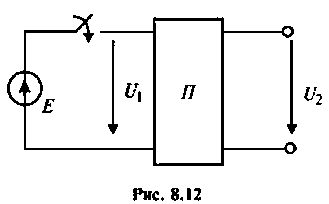
Решение
Применяя преобразования Лапласа, находят изображения
Из прямых преобразований Лапласа и Фурье следует, что
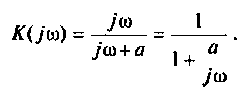
Если принять 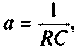
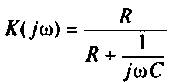
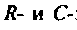
Если принять 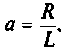
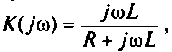
Если принять 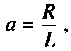
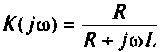
Если принять 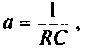
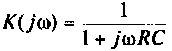
Пример 8.4.4.
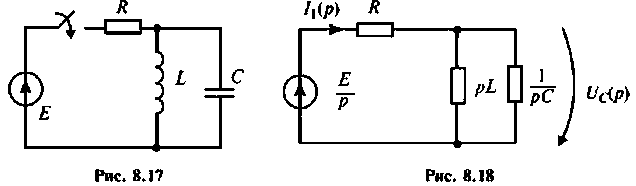
Параллельный колебательный контур (рис. 8.17) включается на постоянное напряжение
Определить напряжение на конденсаторе и построить его опюру, если:
Решение
Определяют независимые начальные условия: напряжение на конденсаторе 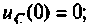
Строят эквивалентную операторную схему замещения после коммутации (рис. 8.18).
Находят изображение напряжения на конденсаторе
По данному изображению находят оригинал по теореме разложения дробно-рациональной функции
где 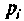
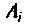
При простых (некратных) полюсах 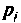
а) Для первого варианта значений:
Полюсы изображения 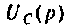
Вычисляют производную 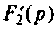
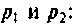
Вычисляют начальные значения компонент
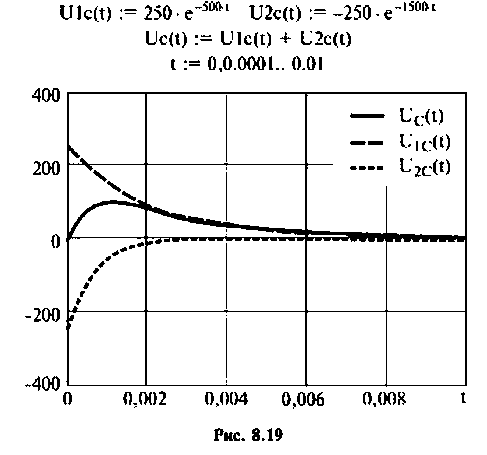
Графики напряжения на конденсаторе и его компонентов получены в среде Mathcad и показаны на рис. 8.19.
Тоn же результат может быть получен по таблице преобразования Лапласа (табл. 8.2, п. 8), если знаменатель изображения напряжения на конденсаторе представить в виде
б) Для второго варианта числовых значений:
а полюсы
Находят производную от 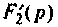
По теореме разложения определяют
где
или
График изменения напряжения 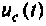
Тот же результат может быть получен по таблице преобразования Лапласа (см. табл. 8.2, п. 13), если знаменатель 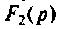
Примечание. Результаты этого примера сравните с результатами примера 6.3. Оцените достоинства и недостатки классического и операторного методов расчета переходных процессов.
Пример 8.4.5.
После замыкания ключа четырехполюсник (рис. 8.21) используется для работы на частоте
а) коэффициент передачи по напряжению 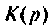
б) характер переходного процесса по кривой переходного процесса.
Дано:
Решение
В режиме холостого хода
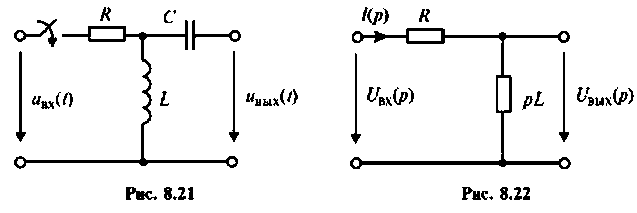
Изображают эквивалентную операторную схему замещения. На рис. 8.22 приведена операторная схема замещения при нулевых начальных условиях.
Находят изображение напряжения на выходе
Определяют полюсы операторной функции из уравнения 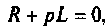
Переходной процесс в цепи имеет апериодический характер, что видно из расположения полюсов на комплексной плоскости (рис, 8.23).
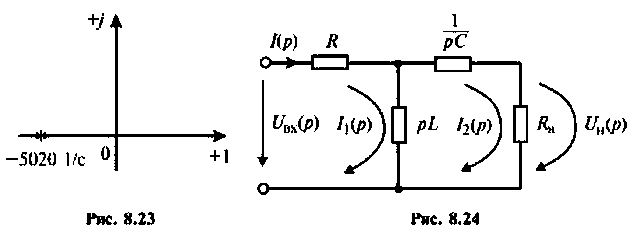
В режиме нагрузки
Изображают эквивалентную операторную схему замещения после коммутации (рис. 8.24).
Определяют операторную функцию 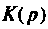
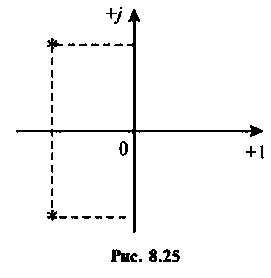
Определяют полюсы операторной функции из уравнения
Для этога вначале вычисляют L и С.
Находят корни уравнения:
Переходный процесс в цепи имеет характер затухающих колебаний, что видно из расположения полюсов на комплексной плоскости (рис. 8.25).
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Метод пространства состояний электрических цепей
- Синтез электрических цепей
- Цепи с распределенными параметрами
- Электрическая энергия, ее свойства и применение
- Переходные процессы в колебательных контурах
- Расчет переходных процессов
- Классический метод расчета переходных процессов
- Анализ переходных и установившихся процессов методом интеграла свертки
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:ОТЦ 2020. ПЗ 04. Анализ переходных процессов в RLC контуре операторным методомСкачать

V. Особенности расчета переходных процессов в цепях с емкостными контурами и индуктивными сечениями
Контуры, состоящие только из емкостей или емкостей и источников ЭДС, называются емкостными контурами.
Сечения, состоящие только из индуктивностей или индуктивностей и источников тока, называют индуктивными сечениями.
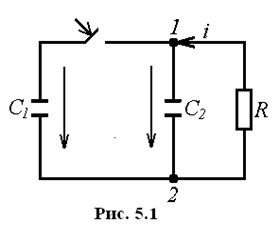
Закон неизменности заряда формулируется следующим образом: алгебраическая сумма зарядов емкостей, присоединенных к любому общему узлу, неизменна в момент коммутации. Т.е. 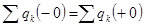
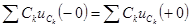
Сумму зарядов записывают с учетом положительных направлений напряжений на емкостях аналогично I закону Кирхгофа для токов, при этом учитывают только емкости емкостных контуров.
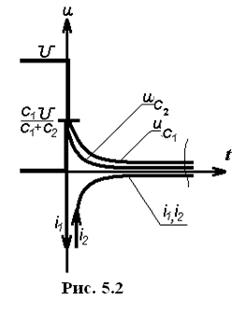
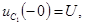
В емкостном контуре имеем два узла 1 и 2. Для любого из этих узлов закон (5.1) принимает вид:

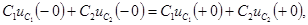
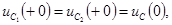
После коммутации цепь описывается уравнением 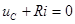
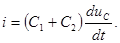
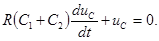
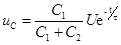
Скачкообразное изменение напряжений обусловлено импульсными токами емкостей, которые возникают в момент коммутации и осуществляют мгновенное перераспределение зарядов между емкостями (рис. 5.2).
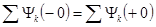
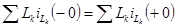
Сумму 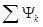
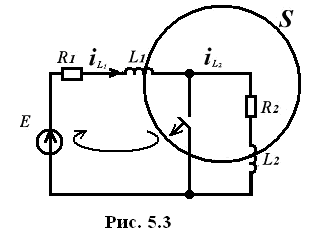
После коммутации цепи (рис. 5.3) имеем один контур, в который входят обе индуктивности сечения s.
Можно записать 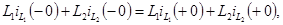
поэтому
После коммутации цепь описывается уравнением:
Решение этого уравнения следующее: 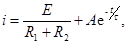
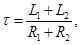
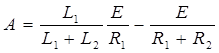
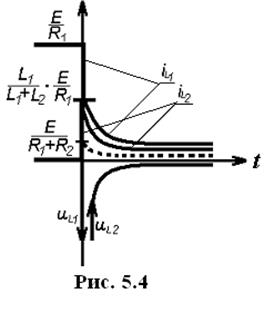

В момент коммутации 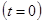
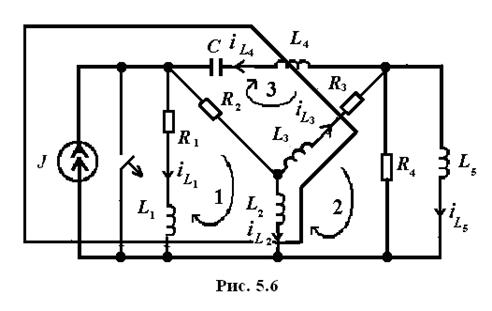
Необходимо составить уравнения для определения начальных значений напряжений на емкостях схемы (рис. 5.5).
После замыкания ключа в схеме образуется емкостной контур 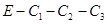
По II закону Кирхгофа для емкостного контура получим уравнение:
Из этих уравнений определим 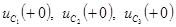
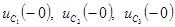
Емкость 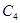
При отключении ключа в схеме образуется индуктивное сечение 
Для указанных на рис. 5.6 трех контуров составим уравнения неизменности потокосцеплений:
По I закону Кирхгофа для сечения получим уравнение:
Из этих уравнений находим
Индуктивность 
Заключение
Рассмотрим достоинства и недостатки расчета переходных процессов рассмотренными методами.
В цепях с характеристическим уравнением первой или второй степени трудности расчета небольшие и примерно одинаковы, каким бы методом ни производили расчет. Классический метод в этих случаях даже несколько проще. Чем выше степень характеристического уравнения, тем больше уравнений нужно решать совместно при определении постоянных интегрирования и тем больше возрастают трудности расчета при пользовании классическим методом. Для разветвленной цепи с характеристическим уравнением выше четвертой или пятой степени расчет классическим методом представляет известные трудности из-за сложности определения четырех и более постоянных интегрирования.
Если цепь представляет собой полный многоугольник, т.е. каждый узел связан ветвью со всеми остальными узлами, то трудности определения постоянных интегрирования, свойственные классическому методу, возрастают с увеличением числа узлов и степени характеристического уравнения. В более простых цепях, когда все узлы не связаны друг с другом, часто можно значительно уменьшить число уравнений, которые нужно решать совместно. В особенности это касается цепей с двумя узлами. В последнем случае, как и в ряде других, разумно ввести в рассмотрение потенциалы узлов.
Таким образом, если степень характеристического уравнения выше четвертой – пятой, классическим методом пользоваться менее целесообразно, а нужно пользоваться операторным методом.
Переходя к операторному методу, сравним два варианта – расчет переходных токов по теореме разложения и расчет свободных токов по их изображениям.
При расчете операторным методом не нужно определять постоянные интегрирования из начальных условий решением какой-либо системы уравнений. Кроме того, при расчете изображений в эквивалентных операторных схемах можно пользоваться всеми ранее известными методами расчета цепей при установившихся режимах. Эти два момента и определяют достоинства операторного метода.
К недостаткам операторного метода надо отнести утомительность вычисления слагаемых сумм в теореме разложения. Если при расчете по теореме разложения находятся сразу переходные токи, то из-за наличия внешних ЭДС (гармонических с разными частотами и экспоненциальных с разными коэффициентами затухания) усложняются многочлены в составе изображения какого-либо тока или напряжения. Если, например, цепь содержит три гармонические ЭДС разной частоты, то число слагаемых в теореме разложения больше степени характеристического уравнения по крайней мере на три. Кроме того, все изображения усложняются за счет внутренних (расчетных) ЭДС 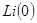
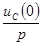
Отметим, что расчет по теореме разложения возможен и для всех таких внешних ЭДС, изображения которых являются отношением двух целых трансцендентных функций.
Расчет операторным методом только свободных токов по их изображениям целесообразен тогда, когда действует ряд различных по характеру внешних ЭДС (гармонических с разными частотами и экспоненциальных с разными коэффициентами затухания). В эквивалентную операторную схему для свободных токов внешние ЭДС не входят, что существенно упрощает изображения токов и напряжений. Однако для определения внутренних (расчетных) ЭДС необходимо рассчитать режим до коммутации и режим после коммутации. Поэтому рассматриваемый вариант операторного метода применим в тех случаях, когда внешние ЭДС имеют простую форму изменения (гармоническую, экспоненциальную, постоянную) и вынужденные токи сравнительно легко найти.
Расчет переходных процессов частотным методом очень близок к расчету операторным методом и характеризуется теми же достоинствами и недостатками. Частотный метод целесообразно применять для расчета переходных процессов в заданной системе в том случае, если для исследования каких-либо других процессов в ней уже применялись частотные методы, аналитическим аппаратом которых является преобразования Фурье. К таким системам относятся, например, линейные системы автоматического регулирования, для которых необходимо исследовать устойчивость при помощи одного из геометрических критериев, исследовать качество регулирования и полностью рассчитать какие-нибудь переходные процессы. Этот метод целесообразно применять при приближенном расчете переходных процессов по вещественной частотной характеристике, особенно когда амплитудная и фазовая частотные характеристики входного сопротивления или проводимости получены экспериментально. В этих случаях метод интеграла Фурье имеет преимущества перед операторным методом. Заметим, что пользуясь операторным методом, входные или взаимные операторные проводимости можно только рассчитать и нельзя получить опытным путем. Проводя же расчет методом интеграла Фурье, получив экспериментально характеристики входных или взаимных проводимостей, имея ЭДС и найдя ее частотный спектр, можно графически найти частотный спектр тока и построить его вещественную или мнимую частотные характеристики. Далее, применяя метод трапеций, можно приближенно рассчитать переходный процесс.
Если напряжение на зажимах пассивного двухполюсника дано кусочно-аналитической кривой, имеющей разрывы, расчет целесообразно вести при помощи интеграла Дюамеля. При этом переходная проводимость или переходная функция находятся одним из известных методов.
Отметим также, что при использовании любым из указанных методов можно задачу расчета переходных процессов с ненулевыми начальными условиями свести к задаче с нулевыми начальными условиями. целесообразность этого приема нужно выяснить в каждом конкретном случае с точки зрения максимально возможного упрощения расчета.
В заключении укажем, что операторный метод и метод интеграла Фурье весьма широко применяются в теории автоматического регулирования и при расчете переходных процессов в электрических машинах, а операторный метод и в некоторой мере метод интеграла Фурье – еще при расчете переходных процессов в цепях с распределенными параметрами, в то время как классический метод во всех этих случаях почти не находит применения.
Видео:Расчёт переходных процессов операторным методомСкачать

II. ОПЕРАТОРНЫЙ МЕТОД РАСЧЕТА
ПЕРЕХОДНЫХ ПРОЦЕССОВ
Основные вопросы
Сущность операторного метода.
Преимущества и недостатки операторного метода по сравнению с классическим методом расчета переходных процессов.
Изображения простейших функций (постоянной, 

Изображения производной и интеграла от функции.
Операторные изображения напряжений на индуктивности и емкости.
Законы Ома и Кирхгофа в операторной форме при нулевых и ненулевых начальных условиях.
Операторный метод нахождения свободных составляющих переходных токов и напряжений (метод Богатырева).
Способы определения оригинала по изображению. Теорема разложения.
Литература
Зевеке Г.В., Ионкин П.А., Нетушил Л.В., Страхов С.В. Основы теории цепей. – М.: Энергия, 1975. – Гл. 19.
Нейман Л.Р., Демирчян К.С. Теоретические основы электротехники. – М.: Энергия, 1966. – Т. 2. – Гл. 10.
Бессонов Л.А. Теоретические основы электротехники. – М.: Высшая школа, 1978. – § 283–310.
Примеры
Задача 1
Индуктивная катушка (рис. а) с параметрами R = 2 Ом; L = 1 Гн включается на напряжение, изменяющееся по закону

Определить мгновенное значение переходного тока и его максимальную величину.
Решение
Эквивалентная операторная схема представлена на рис. б. Операторное изображение источника питания:

Операторное изображение тока (на основании закона Ома):



Поскольку 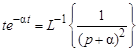

Примерный график переходного тока изображен на рис. в.
Определение максимального значения переходного тока:
а) момент времени t0 соответствует максимуму тока, т.е. экстремуму функции i(t). Поэтому

откуда 

б) максимальное значение переходного тока

Ответ: 

Задача 2

Решение
1. Эквивалентная операторная схема рассматриваемой цепи представлена на рис. б. Операторные изображения стороннего и внутренних источников энергии
2. Операторные ЭДС внутренних источников энергии. На основании законов коммутации 



Следовательно, 



3. Операторное изображение переходного напряжения на индуктивности (рис. б): 
Операторное изображение тока в ветви с индуктивностью целесообразно отыскивать с помощью метода двух узлов. Для схемы (рис. б)



4. Переход к оригиналу. В соответствии с теоремой разложения
f(t) =
переходное напряжение на индуктивности определится соотношением
uL(t) = 
а) корни характеристического уравнения 




б) значения 


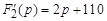



в) переходное напряжение на индуктивности

Ответ: 

В цепи (рис. а) известно: R1 = 50 Ом; R2 = 30 Ом; L = 100 мГн;
C = 200 мкф; U = 1000 B.
Определить ток i1(t) в переходном режиме.
Решение
Эквивалентная операторная схема рассматриваемой цепи представлена на рис. б. Операторные сторонние и внутренние источники энергии: 


Операторные ЭДС внутренних источников энергии. По законам коммутации 



Следовательно, 



Изображение искомого тока. По методу контурных токов (рис. б) (для операторных изображений пригодны все методы расчета стационарных режимов):

Система уравнений (1) после подстановки цифровых значений
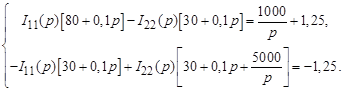
Решение системы (2) относительно I11(p):


Переход к оригиналу. Корни характеристического уравнения F2(p) = 0:

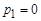



Теорема разложения для случая комплексных корней:
f(t) = L –1 
С учетом того, что 

Ответ:i1(t) = 
Задача 4
L = 0,25 Гн; C = 400 мкФ; f = 50 Гц.

Определить переходный ток i2(t) методом Богатырева.
Решение

Принужденная составляющая искомого тока (отыскивается с помощью символического метода):


Свободная составляющая переходного тока i2(t):
а) эквивалентная операторная схема для свободного режима представлена на рис. б.
б) ЭДС внутренних источников энергии свободного режима:


В соответствии с законами коммутации 

Докоммутационные значения тока в индуктивности и напряжения на емкости (t £ 0)




К моменту коммутации 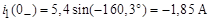

Следовательно, 

Принужденные значения тока в индуктивности и напряжения на емкости




Значения свободных составляющих тока в индуктивности и напряжения на емкости в момент коммутации (t = 0):



в) изображение свободной составляющей искомого тока:
по методу двух узлов (рис. б)


г) оригинал свободной составляющей искомого тока. Корни характеристического уравнения F2(p) = 0:




По теореме разложения в случае комплексных корней
f(t) = L –1 

Общее решение для искомого переходного тока:
Ответ:
🎥 Видео
1 6 3 Операторный метод анализаСкачать

Решение ДУ.Операционный методСкачать

Пример 7 | Операторный метод расчета цепи 1-го порядка с конденсаторомСкачать

13. Операционное исчисление. Решить неоднородное ДУ 2 порядкаСкачать

2015-06-27. Операторный методСкачать

Расчет переходных процессов и построение графиков в Mathcad Prime [операторный метод].Скачать
![Расчет переходных процессов и построение графиков в Mathcad Prime [операторный метод].](https://i.ytimg.com/vi/JGPuEu4do2E/0.jpg)
Лекция 092-3. Расчет переходных процессов операторным методом. Теорема разложенияСкачать

Переходные процессы, операторный методСкачать

Лекция 092-1. Расчет переходных процессов операторным методом. Основные понятияСкачать

Пример 7 | Классический метод расчета цепи 1-го порядка с конденсаторомСкачать

Решение диф.уравнений операторным методомСкачать

14. Операционное исчисление. Система ДУСкачать

Пример 6 | Операторный метод расчета цепи 1-го порядка с конденсаторомСкачать

Лекция 092-2. Расчет переходных процессов операторным методом. Операторная схема замещенияСкачать

Лекция 122. Переходные процессыСкачать

Система дифференциальных уравнений. Операционный методСкачать

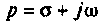
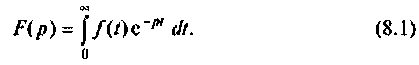
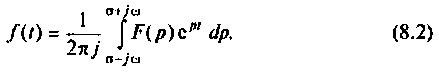
 не возрастала быстрее, чем некоторая показательная функция
не возрастала быстрее, чем некоторая показательная функция