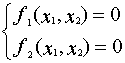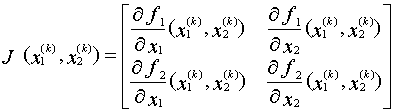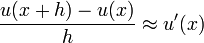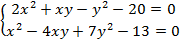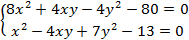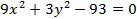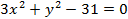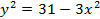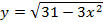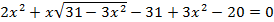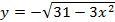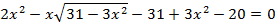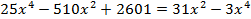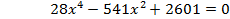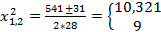Метод ньютона системы двух уравнений

Рассмотрим нелинейную систему уравнений

(5.1)

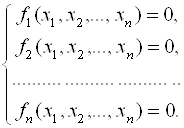
С действительными левыми частями. Систему (5.1) можно представить в матричном виде

(5.2)

Здесь приняты следующие обозначения:

— вектор аргументов, а — вектор – функция.

Для решения системы (5.2) воспользуемся методом последовательных приближений. Предположим, что найдено Р-ое приближение Xp = (X1(P), X2(P) , . Xn(P)) одного из изолированных корней X = (X1, X2, X3, . Xn) векторного уравнения (5.2). Тогда точный корень уравнения (5.2) можно представить в виде

(5.3)

Где — поправка (погрешность) корня на N – ом шаге.

Подставив выражение (5.3) в (5.2), получим

(5.4)

Предположим, что функция F(X) — непрерывно дифференцируема в некоторой выпуклой области, содержащей X и X(P). Тогда левую часть уравнения (5.4) разложим в ряд Тейлора по степеням малого вектора ε(P), ограничиваясь линейными членами:

, (5.5)

Или в развернутом виде:

(5.6)

Из анализа формул (5.5) и (5.6) следует, что под производной F¢(X) следует понимать матрицу Якоби системы функций F1 , F2, . Fn, относительно переменных X1, X2, X3, . Xn, то есть:

. (5.7)

Выражение (5.7) в краткой записи можно представить:

(5.8)

Выражение (5.6) представляет собой линейную систему относительно поправок (I = 1, 2, . N) с матрицей W(X), поэтому формула (5.5) может быть записана в следующем виде:

(5.9)

Отсюда, предполагая, что матрица W(X(P)) — неособенная, получим:

(5.10)

Теперь, подставив выражение (5.10) в формулу (5.3), окончательно получим:

(5.11)

Таким образом, получили вычислительную формулу (метод Ньютона), где в качестве нулевого приближения X(0) можно взять приближенное (грубое) значение искомого корня.

Пример 5.1. Рассмотрим применение метода Ньютона на примере системы двух нелинейных уравнений

(5.12)

Прежде чем разбирать конкретные шаги по решению системы (5.12), распишем в общем виде якобиан для системы из двух уравнений

Здесь A, B, C, D – функционалы от переменных X1, x2. Нас фактически интересует W-1. Пусть матрица W— неособенная, тогда обратная матрица вычисляется

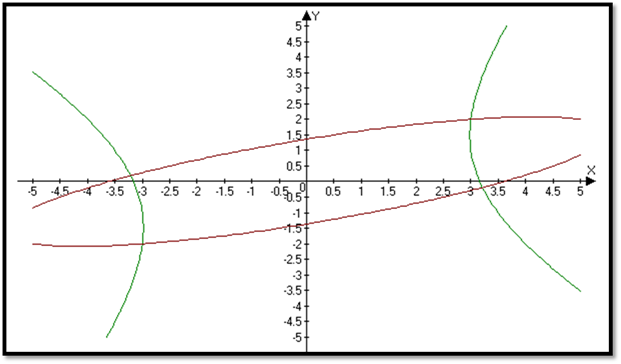
Теперь вернемся к системе (5.12). Графическое решение этой системы дает две точки пересечения: М1 (1.4; -1.5) и М2 (3.4; 2.2). Зададим начальное приближение:

Видео:Метод Ньютона (метод касательных) Пример РешенияСкачать

Нелинейные системы и уравнения

В более общем случае мы имеем не одно уравнение (1), а систему нелинейных уравнений $$ begin tag f_i(x_1, x_2, ldots, x_n) = 0, quad i = 1, 2, ldots n. end $$ Обозначим через ( mathbf = (x_1, x_2, ldots, x_n) ) вектор неизвестных и определим вектор-функцию ( mathbf(mathbf) = (f_1(mathbf), f_2(mathbf), ldots, f_n(mathbf)) ). Тогда система (2) записывается в виде $$ begin tag mathbf(mathbf) = 0. end $$ Частным случаем (3) является уравнение (1) (( n = 1 )). Второй пример (3) — система линейных алгебраических уравнений, когда ( mathbf (mathbf) = A mathbf — mathbf ).

Видео:Алгоритмы С#. Метод Ньютона для решения систем уравненийСкачать

Метод Ньютона

Видео:Метод касательных (метод Ньютона)Скачать

Решение нелинейных уравнений

При итерационном решении уравнений (1), (3) задается некоторое начальное приближение, достаточно близкое к искомому решению ( x^* ). В одношаговых итерационных методах новое приближение ( x_ ) определяется по предыдущему приближению ( x_k ). Говорят, что итерационный метод сходится с линейной скоростью, если ( x_ — x^* = O(x_k — x^*) ) и итерационный метод имеет квадратичную сходимость, если ( x_ — x^* = O(x_k — x^*)^2 ).

В итерационном методе Ньютона (методе касательных) для нового приближения имеем $$ begin tag x_ = x_k + frac, quad k = 0, 1, ldots, end $$

Вычисления по (4) проводятся до тех пор, пока ( f(x_k) ) не станет близким к нулю. Более точно, до тех пор, пока ( |f_(x_k)| > varepsilon ), где ( varepsilon ) — малая величина.

Простейшая реализация метода Ньютона может выглядеть следующим образом:

Чтобы найти корень уравнения ( x^2 = 9 ) необходимо реализовать функции

Данная функция хорошо работает для приведенного примера. Однако, в общем случае могут возникать некоторые ошибки, которые нужно отлавливать. Например: пусть нужно решить уравнение ( tanh(x) = 0 ), точное решение которого ( x = 0 ). Если ( |x_0| leq 1.08 ), то метод сходится за шесть итераций.

Теперь зададим ( x_0 ) близким к ( 1.09 ). Возникнет переполнение

Возникнет деление на ноль, так как для ( x_7 = -126055892892.66042 ) значение ( tanh(x_7) ) при машинном округлении равно ( 1.0 ) и поэтому ( f^prime(x_7) = 1 — tanh(x_7)^2 ) становится равной нулю в знаменателе.

Проблема заключается в том, что при таком начальном приближении метод Ньютона расходится.

Еще один недостаток функции naive_Newton заключается в том, что функция f(x) вызывается в два раза больше, чем необходимо.

Учитывая выше сказанное реализуем функцию с учетом следующего:

1. обрабатывать деление на ноль
2. задавать максимальное число итераций в случае расходимости метода
3. убрать лишний вызов функции f(x)

Метод Ньютона сходится быстро, если начальное приближение близко к решению. Выбор начального приближение влияет не только на скорость сходимости, но и на сходимость вообще. Т.е. при неправильном выборе начального приближения метод Ньютона может расходиться. Неплохой стратегией в случае, когда начальное приближение далеко от точного решения, может быть использование нескольких итераций по методу бисекций, а затем использовать метод Ньютона.

При реализации метода Ньютона нужно знать аналитическое выражение для производной ( f^prime(x) ). Python содержит пакет SymPy, который можно использовать для создания функции dfdx . Для нашей задачи это можно реализовать следующим образом:

Видео:МЗЭ 2021 Лекция 11 Метод Ньютона для решения систем нелинейных уравненийСкачать

Решение нелинейных систем

Идея метода Ньютона для приближенного решения системы (2) заключается в следующем: имея некоторое приближение ( pmb^ ), мы находим следующее приближение ( pmb^ ), аппроксимируя ( pmb(pmb^) ) линейным оператором и решая систему линейных алгебраических уравнений. Аппроксимируем нелинейную задачу ( pmb(pmb^) = 0 ) линейной $$ begin tag pmb(pmb^) + pmb(pmb^)(pmb^ — pmb^) = 0, end $$ где ( pmb(pmb^) ) — матрица Якоби (якобиан): $$ pmb(pmb^) = begin frac<partial f_1(pmb^)> & frac<partial f_1(pmb^)> & ldots & frac<partial f_1(pmb^)> \ frac<partial f_2(pmb^)> & frac<partial f_2(pmb^)> & ldots & frac<partial f_2(pmb^)> \ vdots & vdots & ldots & vdots \ frac<partial f_n(pmb^)> & frac<partial f_n(pmb^)> & ldots & frac<partial f_n(pmb^)> \ end $$ Уравнение (5) является линейной системой с матрицей коэффициентов ( pmb ) и вектором правой части ( -pmb(pmb^) ). Систему можно переписать в виде $$ pmb(pmb^)pmb = — pmb(pmb^), $$ где ( pmb = pmb^ — pmb^ ).

Таким образом, ( k )-я итерация метода Ньютона состоит из двух стадий:

1. Решается система линейных уравнений (СЛАУ) ( pmb(pmb^)pmb = -pmb(pmb^) ) относительно ( pmb ).

2. Находится значение вектора на следующей итерации ( pmb^ = pmb^ + pmb ).

Для решения СЛАУ можно использовать приближенные методы. Можно также использовать метод Гаусса. Пакет numpy содержит модуль linalg , основанный на известной библиотеке LAPACK, в которой реализованы методы линейной алгебры. Инструкция x = numpy.linalg.solve(A, b) решает систему ( Ax = b ) методом Гаусса, реализованным в библиотеке LAPACK.

Когда система нелинейных уравнений возникает при решении задач для нелинейных уравнений в частных производных, матрица Якоби часто бывает разреженной. В этом случае целесообразно использовать специальные методы для разреженных матриц или итерационные методы.

Можно также воспользоваться методами, реализованными для систем линейных уравнений.

Видео:4.2 Решение систем нелинейных уравнений. МетодыСкачать

Метод Ньютона для системы двух уравнений

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ им. Н.Э. БАУМАНА

Отчет по лабораторной работе

по курсу “Численные методы”

Решение систем нелинейных алгебраических

уравнений методом Ньютона»

Студент группы РК6-43

Доцент кафедры ФН-1

Метод Ньютона для нелинейного уравнения

Для решения нелинейного уравнения f(x)=0 по методу Ньютона используется итерационный процесс:

где x (0) — некоторое начальное приближение к корню

При этом предполагается, что f ‘(x)≠ 0 на отрезке [a,b].

Геометрический вывод формулы.

Геометрически итерационный процесс метода Ньютона означает замену на k-той итерации графика функции y=f(x) на касательную к этой функции в точке (x (k) , f(x (k) )) (в связи с этим метод также иногда называется методом касательных). Уравнение касательной имеет вид y=f ‘(x (k) )(x-x (k) )+f(x (k) )

Найдем точку пересечения с осью OX этой касательной (вместо функции y=f(x)), что соответствует нахождению решения линейного уравнения: f ‘(x ( k) )(x-x ( k) )+ f(x ( k) )=0 вместо нелинейного f(x)=0.

Выражая x, получаем: x = x (k) — f(x (k) )/f ‘(x (k) )≡ x (k+1)

Аналитический вывод формулы.

Рассмотрим уравнение f(x)=0, X — его корень, x (k) — k-ое приближение к корню. Тогда по теореме Лагранжа о средних значениях имеем: 0 = f(X) = f(x (k) ) + (X — x (k) )f ‘(c_k ),

Заменяя f ‘(c_k) на значение f ‘(x (k) ) (то есть используя предыдущее приближение к корню) приходим к приближенному равенству 0 ≈ f(x (k) ) + (X — x (k) )f ‘(x (k) ).

Откуда получаем X ≈ x (k) — f(x (k) )/f ‘(x (k) ) ≡ x (k+1)

Метод Ньютона для системы двух уравнений

Рассмотрим систему двух уравнений

Алгоритм решения системы по методу Ньютона задается формулами:

,

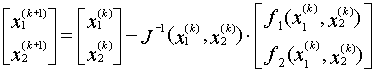(x₁ (0) , x₂ (0) ) — некоторое начальное приближение к корню.

Реализация дифференцирования уравнений системы выполнена методом конечных разностей.

где 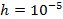– элементарное приращение аргумента

1)

(a)

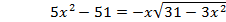
2)

(б)

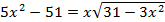
Возведем (а) и (б) в квадрат:

const double EPS = 1E-6;

const double dx = 1E-5;

const double dy = 1E-5;

inline double f1( double x, double y )

return 2.0 * x * x + x * y — y * y — 20.0;

inline double f2( double x, double y )

return x * x — 4.0 * x * y + 7.0 * y * y — 13.0;

static unsigned count = 0;

double a = f1( x[0] + dx, x[1] ) — f1( x[0], x[1] );

double b = f1( x[0], x[1] + dy ) — f1( x[0], x[1] );

double c = f2( x[0] + dx, x[1] ) — f2( x[0], x[1] );

double d = f2( x[0], x[1] + dy ) — f2( x[0], x[1] );

double det_df = a * d — b * c;

double det_1 = 1.0 / det_df;

x[0] = xn[0] — det_1 * ( df_inv[0][0] * f[0] + df_inv[0][1] * f[1] );

x[1] = xn[1] — det_1 * ( df_inv[1][0] * f[0] + df_inv[1][1] * f[1] );

🔥 Видео

Решение системы уравнений методом Крамера 2x2Скачать

Методы решения систем нелинейных уравнений. Метод Ньютона. Численные методы. Лекция 14Скачать

Метод Ньютона | Лучший момент из фильма Двадцать одно 21Скачать

15 Метод Ньютона (Метод касательных) Ручной счет Численные методы решения нелинейного уравненияСкачать

Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать

Метод Ньютона для решения нелинйеных уравнений в MS ExcelСкачать

Методы численного анализа - Метод Ньютона, секущих для решения систем нелинейных уравненийСкачать

МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать

Метод Ньютона (Метод касательных)Скачать

Численный метод Ньютона в ExcelСкачать

4.4 Метод НьютонаСкачать

Вычислительная математика. Лекция 4. Решение нелинейных уравнений и систем уравненийСкачать

7 класс, 37 урок, Системы двух линейных уравнения с двумя переменными. Основные понятияСкачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

После этого видео, ТЫ РЕШИШЬ ЛЮБУЮ Систему Нелинейных УравненийСкачать