Метод ньютона канторовича для нелинейных уравнений

В более общем случае мы имеем не одно уравнение (1), а систему нелинейных уравнений $$ begin tag f_i(x_1, x_2, ldots, x_n) = 0, quad i = 1, 2, ldots n. end $$ Обозначим через ( mathbf = (x_1, x_2, ldots, x_n) ) вектор неизвестных и определим вектор-функцию ( mathbf(mathbf) = (f_1(mathbf), f_2(mathbf), ldots, f_n(mathbf)) ). Тогда система (2) записывается в виде $$ begin tag mathbf(mathbf) = 0. end $$ Частным случаем (3) является уравнение (1) (( n = 1 )). Второй пример (3) — система линейных алгебраических уравнений, когда ( mathbf (mathbf) = A mathbf — mathbf ).

Видео:Метод Ньютона (метод касательных) Пример РешенияСкачать

Метод Ньютона

Видео:Методы численного анализа - Метод Ньютона, секущих для решения систем нелинейных уравненийСкачать

Решение нелинейных уравнений

При итерационном решении уравнений (1), (3) задается некоторое начальное приближение, достаточно близкое к искомому решению ( x^* ). В одношаговых итерационных методах новое приближение ( x_ ) определяется по предыдущему приближению ( x_k ). Говорят, что итерационный метод сходится с линейной скоростью, если ( x_ — x^* = O(x_k — x^*) ) и итерационный метод имеет квадратичную сходимость, если ( x_ — x^* = O(x_k — x^*)^2 ).

В итерационном методе Ньютона (методе касательных) для нового приближения имеем $$ begin tag x_ = x_k + frac, quad k = 0, 1, ldots, end $$

Вычисления по (4) проводятся до тех пор, пока ( f(x_k) ) не станет близким к нулю. Более точно, до тех пор, пока ( |f_(x_k)| > varepsilon ), где ( varepsilon ) — малая величина.

Простейшая реализация метода Ньютона может выглядеть следующим образом:

Чтобы найти корень уравнения ( x^2 = 9 ) необходимо реализовать функции

Данная функция хорошо работает для приведенного примера. Однако, в общем случае могут возникать некоторые ошибки, которые нужно отлавливать. Например: пусть нужно решить уравнение ( tanh(x) = 0 ), точное решение которого ( x = 0 ). Если ( |x_0| leq 1.08 ), то метод сходится за шесть итераций.

Теперь зададим ( x_0 ) близким к ( 1.09 ). Возникнет переполнение

Возникнет деление на ноль, так как для ( x_7 = -126055892892.66042 ) значение ( tanh(x_7) ) при машинном округлении равно ( 1.0 ) и поэтому ( f^prime(x_7) = 1 — tanh(x_7)^2 ) становится равной нулю в знаменателе.

Проблема заключается в том, что при таком начальном приближении метод Ньютона расходится.

Еще один недостаток функции naive_Newton заключается в том, что функция f(x) вызывается в два раза больше, чем необходимо.

Учитывая выше сказанное реализуем функцию с учетом следующего:

1. обрабатывать деление на ноль
2. задавать максимальное число итераций в случае расходимости метода
3. убрать лишний вызов функции f(x)

Метод Ньютона сходится быстро, если начальное приближение близко к решению. Выбор начального приближение влияет не только на скорость сходимости, но и на сходимость вообще. Т.е. при неправильном выборе начального приближения метод Ньютона может расходиться. Неплохой стратегией в случае, когда начальное приближение далеко от точного решения, может быть использование нескольких итераций по методу бисекций, а затем использовать метод Ньютона.

При реализации метода Ньютона нужно знать аналитическое выражение для производной ( f^prime(x) ). Python содержит пакет SymPy, который можно использовать для создания функции dfdx . Для нашей задачи это можно реализовать следующим образом:

Видео:МЗЭ 2021 Лекция 11 Метод Ньютона для решения систем нелинейных уравненийСкачать

Решение нелинейных систем

Идея метода Ньютона для приближенного решения системы (2) заключается в следующем: имея некоторое приближение ( pmb^ ), мы находим следующее приближение ( pmb^ ), аппроксимируя ( pmb(pmb^) ) линейным оператором и решая систему линейных алгебраических уравнений. Аппроксимируем нелинейную задачу ( pmb(pmb^) = 0 ) линейной $$ begin tag pmb(pmb^) + pmb(pmb^)(pmb^ — pmb^) = 0, end $$ где ( pmb(pmb^) ) — матрица Якоби (якобиан): $$ pmb(pmb^) = begin frac<partial f_1(pmb^)> & frac<partial f_1(pmb^)> & ldots & frac<partial f_1(pmb^)> \ frac<partial f_2(pmb^)> & frac<partial f_2(pmb^)> & ldots & frac<partial f_2(pmb^)> \ vdots & vdots & ldots & vdots \ frac<partial f_n(pmb^)> & frac<partial f_n(pmb^)> & ldots & frac<partial f_n(pmb^)> \ end $$ Уравнение (5) является линейной системой с матрицей коэффициентов ( pmb ) и вектором правой части ( -pmb(pmb^) ). Систему можно переписать в виде $$ pmb(pmb^)pmb = — pmb(pmb^), $$ где ( pmb = pmb^ — pmb^ ).

Таким образом, ( k )-я итерация метода Ньютона состоит из двух стадий:

1. Решается система линейных уравнений (СЛАУ) ( pmb(pmb^)pmb = -pmb(pmb^) ) относительно ( pmb ).

2. Находится значение вектора на следующей итерации ( pmb^ = pmb^ + pmb ).

Для решения СЛАУ можно использовать приближенные методы. Можно также использовать метод Гаусса. Пакет numpy содержит модуль linalg , основанный на известной библиотеке LAPACK, в которой реализованы методы линейной алгебры. Инструкция x = numpy.linalg.solve(A, b) решает систему ( Ax = b ) методом Гаусса, реализованным в библиотеке LAPACK.

Когда система нелинейных уравнений возникает при решении задач для нелинейных уравнений в частных производных, матрица Якоби часто бывает разреженной. В этом случае целесообразно использовать специальные методы для разреженных матриц или итерационные методы.

Можно также воспользоваться методами, реализованными для систем линейных уравнений.

Видео:15 Метод Ньютона (Метод касательных) Ручной счет Численные методы решения нелинейного уравненияСкачать

Курсовая работа: Метод Ньютона для решения нелинейных уравнений

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

«Приднестровский государственный университет им. Т.Г. Шевченко»

Кафедра физики, математики и информатики

по дисциплине: «Практикум по решению задач на ЭВМ»

«Метод Ньютона для решения нелинейных уравнений»

студентка III курса;

с доп. специальностью английский

преподаватель Панченко Т. А.

Внедрение ЭВМ во все сферы человеческой деятельности требует от специалистов разного профиля овладения навыками использования вычислительной техники. Повышается уровень подготовки студентов вузов, которые уже с первых курсов приобщаются к использованию ЭВМ и простейших численных методов, не говоря уже о том, при что выполнении курсовых и дипломных проектов применение вычислительной техники становится нормой в подавляющем большинстве вузов.

Вычислительная техника используется сейчас не только в инженерных расчетах и экономических науках, но и таких традиционно нематематических специальностях, как медицина, лингвистика, психология. В связи с этим можно констатировать, что применение ЭВМ приобрело массовый характер. Возникла многочисленная категория специалистов — пользователей ЭВМ, которым необходимы знания по применению ЭВМ в своей отрасли — навыки работы с уже имеющимся программным обеспечением, а также создания своего собственного программного обеспечения, приспособленного для решения конкретной задачи. И здесь на помощь пользователю приходят описания языков программирования высокого уровня и численные методы .

Численные методы разрабатывают и исследуют, как правило, высококвалифицированные специалисты-математики. Для большинства пользователей главной задачей является понимание основных идей и методов, особенностей и областей применения. Однако, пользователи хотят работать с ЭВМ не только как с высокоинтеллектуальным калькулятором, а еще и как с помощником в повседневной работе, хранилищем информации с быстрым и упорядоченным доступом, а так же с источником и обработчиком графической информации. Все эти функции современной ЭВМ я предполагаю продемонстрировать в настоящей курсовой работе.

Видео:Алгоритмы С#. Метод Ньютона для решения систем уравненийСкачать

Цели и задачи.

Целью данной курсовой работы является изучение и реализация в программном продукте решения нелинейных уравнений при помощи метода Ньютона. Данная работа состоит из трёх разделов, заключения и приложения. Первый раздел — теоретический и содержит общие сведения о методе Ньютона. Второй – это практическая часть. Здесь описывается метод Ньютона разобранный на конкретных примерах. Третий посвящён тестированию программы и анализу получившихся результатов. В заключении представлен вывод о проделанной работе.

Цельюданной курсовой работы является программная реализация метода Ньютона для решения нелинейных уравнений.

Для этого необходимо выполнить следующие задачи:

1. Изучить необходимую литературу.

2. Обзорно рассмотреть существующие методы по решению нелинейных уравнений.

3. Изучить метод Ньютона для решения нелинейных уравнений.

4. Рассмотреть решение нелинейных уравнений методом Ньютона на конкретных примерах.

5. Разработать программу для решения нелинейных уравнений методом Ньютона.

6. Проанализировать получившиеся результаты.

Рассмотрим задачу нахождения корней нелинейного уравнения

Корнями уравнения (1) называются такие значения х, которые при подстановке обращают его в тождество. Только для простейших уравнений удается найти решение в виде формул, т.е. аналитическом виде. Чаще приходится решать уравнения приближенными методами, наибольшее распространение среди которых, в связи с появлением компьютеров, получили численные методы.

Алгоритм нахождения корней приближенными методами можно разбить на два этапа. На первом изучается расположение корней и проводится их разделение. Находится область [a,b], в которой существует корень уравнения или начальное приближение к корню x₀ . Простейший способ решения этой задачи является исследование графика функции f(x) . В общем же случае для её решения необходимо привлекать все средства математического анализа.

Существование на найденном отрезке [a,b], по крайней мере, одного корня уравнения (1) следует из условия Больцано:

f(a)*f(b) 0 некоторая константа. Если m=1 , то говорят о сходимости первого порядка; m=2 — о квадратичной, m=3 — о кубической сходимостях.

Итерационные циклы заканчиваются, если при заданной допустимой погрешности выполняются критерии по абсолютным или относительным отклонениям:

; (5,6)

или малости невязки:

(7)

Эта работа посвящена изучению алгоритма решения нелинейных уравнений с помощью метода Ньютона.

Видео:Метод касательных (метод Ньютона)Скачать

1.1 Обзор существующих методов решения нелинейных уравнений

Существует много различных методов решения нелинейных уравнений, некоторые из них представлены ниже:

1)Метод итераций . При решении нелинейного уравнения методом итераций воспользуемся записью уравнения в виде x=f(x). Задаются начальное значение аргумента x₀ и точность ε. Первое приближение решения x₁ находим из выражения x₁ =f(x₀ ), второе — x₂ =f(x₁ ) и т.д. В общем случае i+1 приближение найдем по формуле xi+1 =f(xi). Указанную процедуру повторяем пока |f(xi)|>ε. Условие сходимости метода итераций |f'(x)| ε. Для определения точки пересечения (i+1) касательной с осью абсцисс воспользуемся следующей формулой x_i+1 =x_i -F(x_i ) F’(x_i ). Условие сходимости метода касательных F(x₀ )∙F»(x)>0, и др.

3). Метод дихотомии. Методика решения сводится к постепенному делению начального интервала неопределённости пополам по формуле С_к =а_к +в_к /2.

Для того чтобы выбрать из двух получившихся отрезков необходимый, надо находить значение функции на концах получившихся отрезков и рассматривать тот на котором функция будет менять свой знак, то есть должно выполняться условие f (а_к )* f (в_к ) 0 ;

x* О [a,c] , если f(c)Ч f(b) 0 ;

Метод Ньютона (касательных) характеризуется квадратичной скоростью сходимости, т.е. на каждой итерации удваивается число верных знаков. Однако этот метод не всегда приводит к нужному результату. Рассмотрим этот вопрос подробнее.

Преобразуем уравнение (1) к эквивалентному уравнению вида:

В случае метода касательных . Если известно начальное приближение к корню x=x₀ , то следующее приближение найдем из уравнения x₁ =g(x₀ ), далее x₂ =g(x₁ ). Продолжая этот процесс, получим рекуррентную формулу метода простой итерации

Итерационный процесс продолжается до тех пор, пока не будут выполнены условия (5-7).

Всегда ли описанный вычислительный процесс приводит к искомому решению? При каких условиях он будет сходящимся? Для ответа на эти вопросы опять обратимся к геометрической иллюстрации метода.

Корень уравнения представляется точкой пересечения функций y=x и y=g(x). Как видно из рис. 3(а), если выполняется условие , то процесс сходится, иначе – расходится (рис3(б)).

Итак, для того чтобы итерационный процесс был сходящимся и приводил к искомому результату, требуется выполнение условия:

(12)

Переход от уравнения f(x)=0 к уравнению х=g(x) можно осуществлять различными способами. При этом важно, чтобы выбранная функция g(x) удовлетворяла условию (12). К примеру, если функцию f(x) умножить на произвольную константу q и добавить к обеим частям уравнения (1) переменную х, то g(x)=q*f(x)+x . Выберем константу q такой, чтобы скорость сходимости алгоритма была самой высокой. Если 1 (0) так, чтобы выполнилось условие

Задать малое положительное число ε , как точность вычислений. Положить к = 0.

2. Вычислить х (к+1) по формуле (9) :

.

3. Если | x (k+1) — x (k) | (k+1) . Иначе увеличить к на 1 (к = к + 1) и перейти к пункту 2.

Решим вручную несколько нелинейных уравнений методом Ньютона, а потом сверим результаты с теми, которые получатся при реализации программного продукта.

Решить уравнение методом Ньютона.

sin x 2 + cosx 2 — 10x. = 0.

Вычисления производить с точностью ε = 0, 001.

Вычислим первую производную функции.

F’(x)=2x cosx 2 — 2x sinx 2 — 10.

Теперь вычислим вторую производную от функции.

F’’(x)=2cosx 2 — 4x 2 sinx 2 — 2sinx 2 — 4x 2 cosx 2 = cosx 2 (2-4x 2 ) — sinx 2 (2+4x 2 ).

Построим приближённый график данной функции.

Теперь, исходя из графика, возьмём первый приближённый корень и проверим условие (16) : f(x (0) ) * f’’(x (0) ) > 0.

Пусть x (0) = 0, 565, тогда f(0. 565)*f’’(0. 565) = -4. 387 * (-0. 342) = 1. 5 > 0,

Условие выполняется, значит берём x (0) = 0, 565.

Теперь составим таблицу значений, для решения данного уравнения.

Отсюда следует, что корень уравнения х = 0, 101.

Решить уравнение методом Ньютона.

cos x – e -x2/2 + x — 1 = 0

Вычисления производить с точностью ε = 0, 001.

Вычислим первую производную функции.

F’(x) = 1 – sin x + x*e -x2/2 .

Теперь вычислим вторую производную от функции.

F’’(x) = e -x2/2 *(1-x 2 ) – cos x.

Построим приближённый график данной функции.

Теперь, исходя из графика, возьмём первый приближённый корень и проверим условие (16) : f(x (0) ) * f’’(x (0) ) > 0.

Пусть x (0) = 2, тогда f(2)*f’’(2) = 0. 449 * 0. 010 = 0.05 > 0,

Условие выполняется, значит берём x (0) = 2.

Теперь составим таблицу значений, для решения данного уравнения.

Отсюда следует, что корень уравнения х = 1. 089.

Решить уравнение методом Ньютона.

Вычисления производить с точностью ε = 0, 001.

Вычислим первую производную функции.

Теперь вычислим вторую производную от функции.

Построим приближённый график данной функции.

Теперь, исходя из графика, возьмём первый приближённый корень и проверим условие (16) : f(x (0) ) * f’’(x (0) ) > 0.

Пусть x (0) = 1, тогда f(2)*f’’(2) = 0. 632 * 1, 632 = 1, 031 > 0,

Условие выполняется, значит берём x (0) = 1.

Теперь составим таблицу значений, для решения данного уравнения.

Отсюда следует, что корень уравнения х = 0, 703.

Решить уравнение методом Ньютона.

Вычислим первую производную функции.

F’(x) = -sin x + e -x/2 /2+1.

Теперь вычислим вторую производную от функции.

F’’(x) = -cos x — e -x/2 /4.

Построим приближённый график данной функции.

Теперь, исходя из графика, возьмём первый приближённый корень и проверим условие (16) : f(x (0) ) * f’’(x (0) ) > 0.

Пусть x (0) = 1, тогда f(2)*f’’(2) = -0. 066 * (-0. 692) = 0. 046 > 0,

Условие выполняется, значит берём x (0) = 1.

Теперь составим таблицу значений, для решения данного уравнения.

Отсюда следует, что корень уравнения х = 1. 162.

Решить уравнение методом Ньютона.

Вычислим первую производную функции.

Теперь вычислим вторую производную от функции.

Построим приближённый график данной функции.

Теперь, исходя из графика, возьмём первый приближённый корень и проверим условие (16) : f(x (0) ) * f’’(x (0) ) > 0.

Пусть x (0) = 1, тогда f(2)*f’’(2) = 0. 350 * 2, 350 = 0. 823 > 0,

Условие выполняется, значит берём x (0) = 1.

Теперь составим таблицу значений, для решения данного уравнения.

Отсюда следует, что корень уравнения х = 0, 881.

Видео:Методы решения систем нелинейных уравнений. Метод Ньютона. Численные методы. Лекция 14Скачать

3.1 Описание программы

Данная программа создана для работы в текстовом и графическом режиме. Она состоит из модуля Graph, Crt, трёх функций и трёх процедур.

1. модуль Crt предназначен для обеспечения контроля над текстовыми режимами экрана, расширенными кодами клавиатуры, цветами, окнами и звуком;

2. модуль Graph предназначен для обеспечения контроля над графическими объектами;

3. procedure GrafInit — инициализирует графический режим;

4. function VF – вычисляет значение функции;

5. function f1 – вычисляет значение первой производной функции;

6. function X_Newt – реализует алгоритм решения уравнения методом Ньютона.

7. procedure FGraf – реализует построение графика заданной функции f(x);

Ots=35 — константа, определяющая количество точек для отступа от границ монитора;

fmin, fmax – максимальные и минимальные значения функции;

SetColor(4) – процедура, которая устанавливает текущий цвет графического объекта, используя палитру, в данном случае это красный цвет;

SetBkColor(9) – процедура, которая устанавливает текущий цвет фона, используя палитру, в данном случае – это светло-синий цвет.

8. Procedure MaxMinF – вычислят максимальные и минимальные значения функции f(x).

Line – процедура, которая рисует линию из точки с координатами (x1, у1) в точку с координатами (х2, у2);

MoveTo – процедура, перемещающая указатель (СР) в точку с координатами (х, у);

TextColor(5) – процедура, устанавливающая текущий цвет символов, в данном случае – это розовый;

Outtexty(х, у, ‘строка’) – процедура, которая выводит строку, начиная с позиции (х, у)

CloseGraph – процедура, закрывающая графическую систему.

Видео:Решение нелинейного уравнения методом Ньютона (касательных) (программа)Скачать

3.2 Тестирование программы

Для тестирования программы возьмем те примеры, которые решали в практической части работы, чтобы сверить результаты и проверить правильность работы программы.

1) sin x 2 + cosx 2 — 10x. = 0.

Данная программа вычисляет корни нелинейного уравнения методом Ньютона с точностью eps и чертит приблизительный график функции на отрезке [a, b].

Введите точность вычисления eps=0. 01

Корень уравнения, найденный методом Ньютона:

сделаем проверку, подставив полученный ответ в уравнение.

Получим : х=0, 0000002

2) cos x – e -x2/2 + x — 1 = 0.

Данная программа вычисляет корни нелинейного уравнения методом Ньютона с точностью eps и чертит приблизительный график функции на отрезке [a, b].

Введите точность вычисления eps=0. 001

Корень уравнения, найденный методом Ньютона:

сделаем проверку, подставив полученный ответ в уравнение.

Получим : х=-0, 0000000

Данная программа вычисляет корни нелинейного уравнения методом Ньютона с точностью eps и чертит приблизительный график функции на отрезке [a, b].

Введите точность вычисления eps=0. 01

Корень уравнения, найденный методом Ньютона:

сделаем проверку, подставив полученный ответ в уравнение.

Получим : х=0, 0000000

4) cos x –e -x/2 +x-1=0.

Данная программа вычисляет корни нелинейного уравнения методом Ньютона с точностью eps и чертит приблизительный график функции на отрезке [a, b].

Введите точность вычисления eps=0. 001

Корень уравнения, найденный методом Ньютона:

сделаем проверку, подставив полученный ответ в уравнение.

Получим : х=0, 0008180

Данная программа вычисляет корни нелинейного уравнения методом Ньютона с точностью eps и чертит приблизительный график функции на отрезке [a, b].

Введите точность вычисления eps=0. 001

Корень уравнения, найденный методом Ньютона:

Сделаем проверку, подставив полученный ответ в уравнение.

Получим : х=0, 0000000

Целью работы было создать программу, которая вычисляет корень нелинейного уравнения методом Ньютона. Исходя из этого, можно сделать вывод, что цель достигнута, так как для ее осуществления были решены следующие задачи:

1.Изучена необходимая литература.

2.Обзорно рассмотрены существующие методы по решению нелинейных уравнений.

3.Изучен метод Ньютона для решения нелинейных уравнений.

4.Рассмотрено решение нелинейных уравнений методом Ньютона на примере.

5.Проведены тестирование и отладка программы.

Видео:Метод Ньютона для решения нелинйеных уравнений в MS ExcelСкачать

Список используемой литературы

1. Б.П. Демидович, И.А Марон. Основы вычислительной математики. – Москва, изд. «Наука»; 1970.

2. В.М. Вержбицкий. Численные методы (линейная алгебра и нелинейные уравнения). – Москва, «Высшая школа»; 2000.

3. Н.С.Бахвалов, А.В.Лапин, Е.В.Чижонков. Численные методы в задачах и упражнениях. – Москва, «Высшая школа»; 2000.

4. Мэтьюз, Джон, Г.,Финк, Куртис, Д. Численные методы MATLAB, 3-е издание.- Москва, «Вильяс»; 2001.

Видео:Метод Ньютона | Лучший момент из фильма Двадцать одно 21Скачать

5.1. Приближённое решение систем нелинейных уравнений. Метод Ньютона

Рассмотрим нелинейную систему уравнений

(5.1)

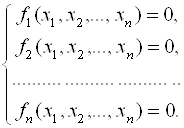
С действительными левыми частями. Систему (5.1) можно представить в матричном виде

(5.2)

Здесь приняты следующие обозначения:

— вектор аргументов, а — вектор – функция.

Для решения системы (5.2) воспользуемся методом последовательных приближений. Предположим, что найдено Р-ое приближение Xp = (X1(P), X2(P) , . Xn(P)) одного из изолированных корней X = (X1, X2, X3, . Xn) векторного уравнения (5.2). Тогда точный корень уравнения (5.2) можно представить в виде

(5.3)

Где — поправка (погрешность) корня на N – ом шаге.

Подставив выражение (5.3) в (5.2), получим

(5.4)

Предположим, что функция F(X) — непрерывно дифференцируема в некоторой выпуклой области, содержащей X и X(P). Тогда левую часть уравнения (5.4) разложим в ряд Тейлора по степеням малого вектора ε(P), ограничиваясь линейными членами:

, (5.5)

Или в развернутом виде:

(5.6)

Из анализа формул (5.5) и (5.6) следует, что под производной F¢(X) следует понимать матрицу Якоби системы функций F1 , F2, . Fn, относительно переменных X1, X2, X3, . Xn, то есть:

. (5.7)

Выражение (5.7) в краткой записи можно представить:

(5.8)

Выражение (5.6) представляет собой линейную систему относительно поправок (I = 1, 2, . N) с матрицей W(X), поэтому формула (5.5) может быть записана в следующем виде:

(5.9)

Отсюда, предполагая, что матрица W(X(P)) — неособенная, получим:

(5.10)

Теперь, подставив выражение (5.10) в формулу (5.3), окончательно получим:

(5.11)

Таким образом, получили вычислительную формулу (метод Ньютона), где в качестве нулевого приближения X(0) можно взять приближенное (грубое) значение искомого корня.

Пример 5.1. Рассмотрим применение метода Ньютона на примере системы двух нелинейных уравнений

(5.12)

Прежде чем разбирать конкретные шаги по решению системы (5.12), распишем в общем виде якобиан для системы из двух уравнений

Здесь A, B, C, D – функционалы от переменных X1, x2. Нас фактически интересует W-1. Пусть матрица W— неособенная, тогда обратная матрица вычисляется

Теперь вернемся к системе (5.12). Графическое решение этой системы дает две точки пересечения: М1 (1.4; -1.5) и М2 (3.4; 2.2). Зададим начальное приближение:

🌟 Видео

4.2 Решение систем нелинейных уравнений. МетодыСкачать

Метод Ньютона (Метод касательных)Скачать

10 Численные методы решения нелинейных уравненийСкачать

11 Метод Ньютона (Метод касательных) Mathcad Численные методы решения нелинейного уравненияСкачать

Численный метод Ньютона в ExcelСкачать

Метод Ньютона, или Извлечение квадратного корняСкачать

Численное решение уравнений, урок 4/5. Метод касательных (Ньютона)Скачать

После этого видео, ТЫ РЕШИШЬ ЛЮБУЮ Систему Нелинейных УравненийСкачать

Способы решения систем нелинейных уравнений. 9 класс.Скачать

10 Метод Ньютона (Метод касательных) C++ Численные методы решения нелинейного уравненияСкачать