Метод ньютона для решения уравнений в excel

Видео:Метод Ньютона для решения нелинйеных уравнений в MS ExcelСкачать

Метод Ньютона в Excel

Как видно, процесс нахождения корней нелинейного уравнения методом Ньютона состоит из следующих этапов:

1. Получения шаблона.
2. Уточнение интервалов в ячейках B2 , B3 .
3. Замена в формуле ЕСЛИ запятую ( , ) на точку с запятой ( ; ).
4. Копирование строки итераций до требуемой точности (столбец E ).

Примечание: столбец A — номер итерации, столбец B — корень уравнения X , столбец C — значение функции F(X) , столбец D — значение первой производной dF(X) , столбец E — точность eps .

Видео:Численный метод Ньютона в ExcelСкачать

Трансцендентные уравнения? «Подбор параметра» в Excel!

Нелинейные, трансцендентные уравнения функции одной переменной – это уравнения вида f (x) = 0, в которых нельзя найти алгебраическими методами корни. Функция f (x) – это, как правило, достаточно сложная и громоздкая функция, содержащая в своем составе.

. тригонометрические, логарифмические, степенные и иные нелинейные функции с различной глубиной вложенности. Например: f (x) = sin (3,14^x) + cos (x) = 0. Уравнения такого вида решаются численными методами.

В этой статье я постараюсь доступно и кратко рассказать и показать на примерах, как и когда такие задачи возникают и как их сегодня быстро и просто можно решать в Excel.

Видео:Численное решение уравнений, урок 4/5. Метод касательных (Ньютона)Скачать

Чуть-чуть истории и теории.

Вы задумывались когда-нибудь — откуда и зачем в головах людей, живших в XVI…XVII веках, родились понятия дифференциалов, производных, интегралов? Объяснение, в общем-то, достаточно простое и понятное – эти ученые искали аналитические пути решения прикладных практических задач. И успешно находили.

Мне сегодня видится приблизительно такая «лестница» с качественными «ступенями инструментов» математики для решения практических и научных задач, которую изобрело человечество:

1. Арифметика — сложение, вычитание, умножение, деление.

2. Алгебра – применение элементарных функций (степенной, логарифмической, тригонометрической, …) и алгебраических уравнений функции одной переменной.

3. Гауссовские системы линейных уравнений.

4. Численные методы решения трансцендентных уравнений.

5. Численные методы решения систем трансцендентных уравнений функций нескольких переменных.

6. Дифференцирование и интегрирование функций одной переменной.

7. Дифференцирование и интегрирование функций нескольких переменных.

8. Системы дифференциальных и интегральных уравнений.

9. Масса разнообразных новых и старых специальных методик и подходов мне не известных и известных, но, безусловно, существующих и работающих.

Предлагаю остановиться и разобраться с достаточно высокой четвертой ступенью «лестницы».

Для численного решения нелинейных уравнений успешно применяются: метод половинного деления, метод простых итераций, метод хорд, метод касательных Ньютона, комбинированный метод секущих-хорд на основе итерационной формулы Ньютона. Для чего ученые-математики придумали множество различных методов решения трансцендентных уравнений? Они старались упростить и ускорить процесс расчетов. Надо помнить и понимать, что у них компьютеров не было, и расчеты выполнялись вручную.

Каждый из методов имеет свои достоинства и недостатки — они подробно описаны в литературе, и углубляться в них мы не будем. Скажу только, что из вышеперечисленных методов мне на практике довелось использовать все. При решении различных (в основном геометрических и теплотехнических) задач по разным причинам было удобно использовать то один, то другой подход. Метод Ньютона хорош своей быстрой сходимостью и простотой формулы. Комбинированный метод секущих-хорд на основе итерационной формулы Ньютона не требует нахождения производных, быстро «сходится», и главное – не требует анализа функции на сходимость. Метод половинного деления медленно сходится, но не требует никакого предварительного анализа функции.

Видео:Алгоритмы С#. Метод Ньютона для решения систем уравненийСкачать

Трансцендентные уравнения. Два метода решения в Excel.

Если у вас на компьютере нет программы MS Excel, то расчеты можно выполнить в программе OOo Calc из бесплатного пакета Open Office.

Задач, которые требуют для получения ответа составления и решения трансцендентных уравнений, вокруг нас очень много. Это — задачи и физики, и теплотехники, и астрономии, и элементарной геометрии в обычной жизни… Инженерам-конструкторам и программистам в повседневной работе необходимо уметь составлять и быстро решать численными методами нелинейные уравнения. На мой взгляд — это один из критериев профессионализма. Более того, уравнения, которые решаются аналитически, сегодня иногда гораздо проще и быстрее при наличии вычислительной техники решить численными методами, поэтому нужно уметь это делать.

Вычисление угла зацепления зубчатой передачи методом Ньютона (методом касательных)

Рассмотрим пример из статьи «Расчет геометрии зубчатой передачи». Необходимо найти угол зацепления зубчатой передачи atw . Я обещал в той статье рассказать, как это делается. Выполняю обещание.

Если расстояние между центрами колеса и шестерни не задано, то угол зацепления можно вычислить путем решения трансцендентного уравнения:

inv ( atw )=tg ( atw ) — atw =2* xs *tg ( a )/( z2 + T * z1 )+ tg ( at ) — at

Подставив данные из примера, рассмотренного в вышеупомянутой статье, получим после преобразований следующее уравнение:

inv ( atw )=0,020910

f ( atw )=tg ( atw )— atw -0,020910=0

Используем метод Ньютона, потому что взять производную представленной выше функции элементарно просто, а итерационная формула очень проста и компактна:

f’( atw )=1/(cos ( atw ))^2—1

atw (i+1) = atw i — f ( atw ) i/ f’( atw ) i

Открываем файл Excel и начинаем работу.

Исходные данные будем традиционно писать в ячейки со светло-бирюзовой заливкой. Результаты расчетов будем считывать в ячейках со светло-желтой заливкой.

1. Инволюту угла зацепления inv( atw ) заносим

в ячейку D3: 0,020910

2. Значение угла зацепления в нулевом приближении atw 0 в радианах записываем

3. Итерационную формулу atw (i+1)= atw i— f( atw )i/ f’( atw )i заносим

в D5: =D4- (TAN (D4) -D4-$D$3)/(1/(COS (D4))^2-1) =0,591706

atw 1= atw 0- (tg ( atw 0) — atw 0- inv ( atw ))/(1/(cos ( atw 0))^2-1)

и копируем в ячейки D6… D14

4. Видим, что уже после шестой итерации угол зацепления atw в радианах вычислен с нулевой абсолютной и относительной ошибкой:

atw =D13- (TAN (D13) -D13-$D$3)/(1/(COS (D13))^2-1) =0,389140

Решение найдено, расчет в Excel завершен!

Решение задачи ландшафтного дизайна с помощью сервиса «Подбор параметра» в Excel

Задача:

Вдоль отмостки стены дома длиной 14 метров необходимо разбить цветник в виде сегмента круга площадью ровно 16 квадратных метров. На сколько метров цветник будет отстоять от края отмостки по центру стены? Каким радиусом необходимо выполнить границу цветника?

1. Длину отмостки стены дома — хорды сегмента круга x в метрах записываем

в ячейку D17: 14,000

2. Площадь цветника – сегмента круга S в квадратных метрах вписываем

в D18: 16,000

3. Предположительное произвольное (не нулевое) значение центрального угла сегмента a в радианах пишем

Трансцендентное уравнение a / sin( a /2 ) -2*cos ( a /2) — (8* S / x ^2) *sin( a /2)=0 вводим

в объединенную ячейку E19F19: =D19/SIN (D19/2) -2*COS (D19/2) — (8*D18/D17^2)*SIN (D19/2)

Включаем сервис «Подбор параметра» в Excel: «Сервис» – «Подбор параметра». Пишем в появившемся окне все как на рисунке слева и нажимаем кнопку OK.

В появившемся новом окне видим, что решение найдено, снова нажимаем на кнопку OK.

Считываем искомое значение центрального угла сегмента a в радианах

в D19: 0,950057

При этом видим, что значение трансцендентного уравнения равно нулю; считываем

в объединенной ячейке E19F19: =D19/SIN (D19/2) -2*COS (D19/2) — (8*D18/D17^2)*SIN (D19/2) =0

4. Радиус наружной границы цветника – радиус сегмента круга r в метрах рассчитывается

в D20: =D17/2/SIN (D19/2) =15,305

r = x /2/sin( a /2)

5. Максимальная ширина цветника – высота сегмента круга h в метрах рассчитывается

в ячейке D21: =D20*(1-COS (D19/2)) =1.695

h = r *(1- cos( a /2))

Ответы получены, вторая задача успешно решена!

Я не приводил вывода использованных формул потому, что это не по теме поста, и, думаю, с геометрией и тригонометрией вы легко разберетесь. Будут вопросы – обращайтесь.

Чтобы получать информацию о выходе новых статей вам нужно подписаться на анонсы в окне, расположенном вверху страницы. Введите адрес своей электронной почты и нажмите на кнопку «Получать анонсы статей». С этого момента к вам на почтовый ящик будет приходить небольшое уведомление о появлении на моем блоге новой статьи.

Видео:Решение системы уравнений в ExcelСкачать

Краткие выводы

1. Итерационными численными методами удобно и быстро можно решать трансцендентные уравнения и громоздкие нелинейные алгебраические.

2. При написании расчетных модулей программ в Excel, если нежелательны лишние остановки по ходу вычислений, можно использовать вставки блоков с классическими методами решения нелинейных уравнений или макросов с вызовом инструмента «Подбор параметра».

3. Использование инструмента «Подбор параметра» в Excel является сегодня, безусловно, наиболее оптимальным и эффективным методом решения нелинейных, трансцендентных уравнений функций одной переменной, а также проведения анализа типа «Что будет? Если…».

Умение применять в работе сервис «Подбор параметра» существенно повышает ваш уровень, как специалиста вообще, так и как пользователя Excel – в частности.

Буду очень рад увидеть ваши комментарии к статье, уважаемые читатели!

Видео:Метод Ньютона (метод касательных) Пример РешенияСкачать

Решение уравнений средствами EXCEL

Идея метода

Нелинейные уравнения

Аналитическое решение нелинейных уравнений существует только для узкого круга типов уравнений. Доказано, что алгебраические уравнения выше четвертой степени неразрешимы в элементарных функциях. Поэтому решение уравнения сводят к численному решению.

Нахождение приближенного решения проводят в два этапа. На первом этапе производится отделение корней – поиск интервалов, в которых содержится только по одному корню. Второй этап решения связан с уточнением корня в выбранном интервале (определением значения корня с заданной точностью).

В общем случае отделение корней уравнения f(x)=0 базируется на известной теореме, утверждающей, что если непрерывная функция f(x) на концах отрезка [a,b] имеет значения разных знаков, т.е. f(a)×f(b)≤0, то в указанном промежутке содержится хотя бы один корень. Например, для уравнения f(x) = x 3 -6x+2 = 0 видим, что при x →∞ f(x)>0, при x → — ∞ f(x) n -6 ) после десятичной точки достаточно провести 20 вычислений (итераций) значений функции.

Метод Ньютона

Данный метод еще называют методом касательных, т.к. основная идея метода заключается в последовательном построении касательных в точках, выбираемых по определенному алгоритму. Причем первая точка, называемая начальным приближением, выбирается заранее. Пусть известно некоторое приближенное значение Z_n корня X * . Применяя формулу Тейлора и ограничиваясь в ней

двумя членами, имеем

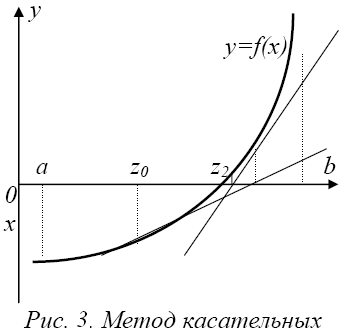Геометрическое решение этого метода заключается, как упоминалось ранее, в построении касательной к кривой y = f(x) в выбранной точке x = Z_n. Далее находится точка пересечения этой касательной с осью абсцисс, и эта точка принимается за очередное приближение к корню (рис. 3).

Решение уравнений средствами EXCEL

🔍 Видео

Решение системы нелинейных уравнений графическим способом средствами ExcelСкачать

12 Метод Ньютона (Метод касательных) Excel Calc Численные методы решения нелинейного уравненияСкачать

Метод касательныхСкачать

Решение уравнений с помощью ExcelСкачать

Как найти корни уравнения в Excel с помощью Подбора параметраСкачать

Численное решение уравнений, урок 3/5. Метод хордСкачать

Решение системы линейных алгебраических уравнений (СЛАУ) в Excel МАТРИЧНЫМ МЕТОДОМСкачать

15 Метод Ньютона (Метод касательных) Ручной счет Численные методы решения нелинейного уравненияСкачать

Решение системы уравнения с помощью настройки поиск решенияСкачать

Метод простых итераций пример решения нелинейных уравненийСкачать

5.1 Численные методы решения уравнений F(x)=0Скачать

Метод касательных (метод Ньютона)Скачать

8 Метод половинного деления Calc Excel Численные методы решения нелинейного уравненияСкачать

Численное решение уравнений, урок 5/5. Комбинированный метод хорд и касательныхСкачать