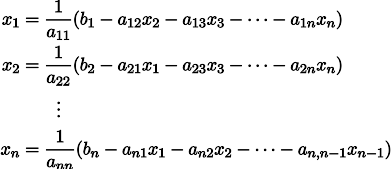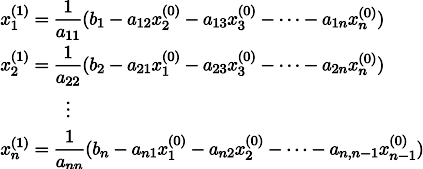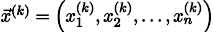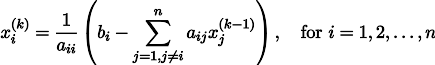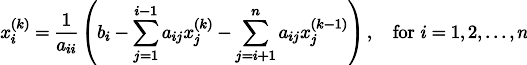Метод наименьших квадратов решения несовместных систем линейных алгебраических уравнений

Видео:Как работает метод наименьших квадратов? Душкин объяснитСкачать

Методы наименьших квадратов без слёз и боли

Итак, очередная статья из цикла «математика на пальцах». Сегодня мы продолжим разговор о методах наименьших квадратов, но на сей раз с точки зрения программиста. Это очередная статья в серии, но она стоит особняком, так как вообще не требует никаких знаний математики. Статья задумывалась как введение в теорию, поэтому из базовых навыков она требует умения включить компьютер и написать пять строк кода. Разумеется, на этой статье я не остановлюсь, и в ближайшее же время опубликую продолжение. Если сумею найти достаточно времени, то напишу книгу из этого материала. Целевая публика — программисты, так что хабр подходящее место для обкатки. Я в целом не люблю писать формулы, и я очень люблю учиться на примерах, мне кажется, что это очень важно — не просто смотреть на закорючки на школьной доске, но всё пробовать на зуб.

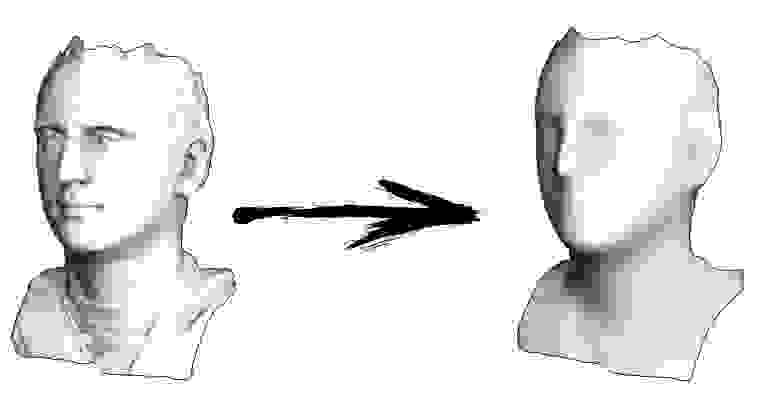
Итак, начнём. Давайте представим, что у меня есть триангулированная поверхность со сканом моего лица (на картинке слева). Что мне нужно сделать, чтобы усилить характерные черты, превратив эту поверхность в гротескную маску?

В данном конкретном случае я решаю эллиптическое дифференциальное уравнение, носящее имя Симеона Деми Пуассона. Товарищи программисты, давайте сыграем в игру: прикиньте, сколько строк в C++ коде, его решающем? Сторонние библиотеки вызывать нельзя, у нас в распоряжении только голый компилятор. Ответ под катом.

На самом деле, двадцати строк кода достаточно для солвера. Если считать со всем-всем, включая парсер файла 3Д модели, то в двести строк уложиться — раз плюнуть.

Видео:Метод наименьших квадратов. Линейная аппроксимацияСкачать

Пример 1: сглаживание данных

Давайте расскажу, как это работает. Начнём издалека, представьте, что у нас есть обычный массив f, например, из 32 элементов, инициализированный следующим образом:

А затем мы тысячу раз выполним следующую процедуру: для каждой ячейки f[i] мы запишем в неё среднее значение соседних ячеек: f[i] = ( f[i-1] + f[i+1] )/2. Чтобы было понятнее, вот полный код:

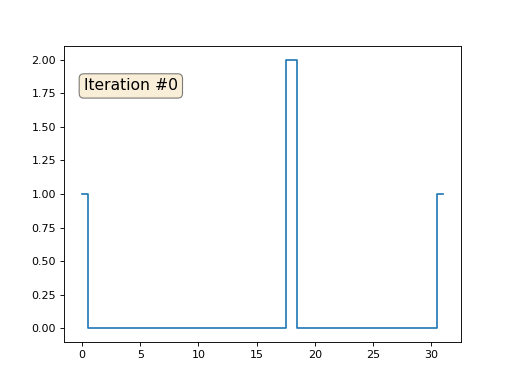
Каждая итерация будет сглаживать данные нашего массива, и через тысячу итераций мы получим постоянное значение во всех ячейках. Вот анимация первых ста пятидесяти итераций:

Если вам неясно, почему происходит сглаживание, прямо сейчас остановитесь, возьмите ручку и попробуйте порисовать примеры, иначе дальше читать не имеет смысла. Триангулированная поверхность ничем принципиально от этого примера не отличается. Представьте, что для каждой вершины мы найдём соседние с ней, посчитаем их центр масс, и передвинем нашу вершину в этот центр масс, и так десять раз. Результат будет вот таким:

Разумеется, если не остановиться на десяти итерациях, то через некоторое время вся поверхность сожмётся в одну точку ровно так же, как и в предыдущем примере весь массив стал заполнен одним и тем же значением.

Видео:11 4 Применение МНК к решению систем линейных уравненийСкачать

Пример 2: усиление/ослабление характеристических черт

Полный код доступен на гитхабе, а здесь я приведу самую важную часть, опустив лишь чтение и запись 3Д моделей. Итак, триангулированная модель у меня представлена двумя массивами: verts и faces. Массив verts — это просто набор трёхмерных точек, они же вершины полигональной сетки. Массив faces — это набор треугольников (количество треугольников равно faces.size()), для каждого треугольника в массиве хранятся индексы из массива вершин. Формат данных и работу с ним я подробно описывал в своём курсе лекций по компьютерной графике. Есть ещё третий массив, который я пересчитываю из первых двух (точнее, только из массива faces) — vvadj. Это массив, который для каждой вершины (первый индекс двумерного массива) хранит индексы соседних с ней вершин (второй индекс).

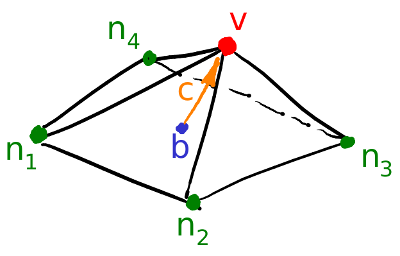
Первое, что я делаю, это для каждой вершины моей поверхности считаю вектор кривизны. Давайте проиллюстрируем: для текущей вершины v я перебираю всех её соседей n1-n4; затем я считаю их центр масс b = (n1+n2+n3+n4)/4. Ну и финальный вектор кривизны может быть посчитан как c=v-b, это не что иное, как обычные конечные разности для второй производной.

Непосредственно в коде это выглядит следующим образом:

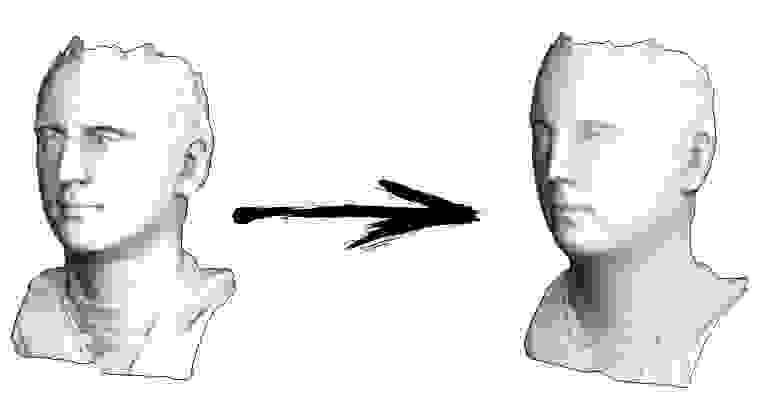
Ну а дальше мы много раз делаем следующую вещь (смотрите предыдущую картинку): мы вершину v двигаем v := b + const * c. Обратите внимание, что если константа равна единице, то наша вершина никуда не сдвинется! Если константа равна нулю, то вершина заменяется на центр масс соседних вершин, что будет сглаживать нашу поверхность. Если константа больше единицы (заглавная картинка сделана при помощи const=2.1), то вершина будет сдвигаться в направлении вектора кривизны поверхности, усиливая детали. Вот так это выглядит в коде:

Кстати, если меньше единицы, то детали будут наоборот ослабляться (const=0.5), но это не будет эквивалентно простому сглаживанию, «контраст картинки» останется:

Обратите внимание, что мой код генерирует файл 3Д модели в формате Wavefront .obj, рендерил я в сторонней программе. Посмотреть получившуюся модель можно, например, в онлайн-вьюере. Если вам интересны именно методы отрисовки, а не генерирование модели, то читайте мой курс лекций по компьютерной графике.

Видео:Приближение методом наименьших квадратов. Решение СЛАУ с минимизацией среднеквадратичного отклоненияСкачать

Пример 3: добавляем ограничения

Давайте вернёмся к самому первому примеру, и сделаем ровно то же самое, но только не будем переписывать элементы массива под номерами 0, 18 и 31:

Остальные, «свободные» элементы массива я инициализировал нулями, и по-прежнему итеративно заменяю их на среднее значение соседних элементов. Вот так выглядит эволюция массива на первых ста пятидесяти итерациях:

Вполне очевидно, что на сей раз решение сойдётся не к постоянному элементу, заполняющему массив, а к двум линейным рампам. Кстати, действительно ли всем очевидно? Если нет, то экспериментируйте с этим кодом, я специально привожу примеры с очень коротким кодом, чтобы можно было досконально разобраться с происходящим.

Видео:Метод наименьших квадратов. ТемаСкачать

Лирическое отступление: численное решение систем линейных уравнений.

Пусть нам дана обычная система линейных уравнений:

Её можно переписать, оставив в каждом из уравнений с одной стороны знака равенства x_i:

Пусть нам дан произвольный вектор 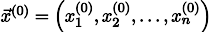, приближающий решение системы уравнений (например, нулевой).

Тогда, воткнув его в правую часть нашей системы, мы можем получить обновлённый вектор приближения решения .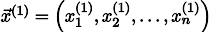

Чтобы было понятнее, x1 получается из x0 следующим образом:

Повторив процесс k раз, решение будет приближено вектором

Давайте на всякий случай запишем рекурретную формулу:

При некоторых предположениях о коэффициентах системы (например, вполне очевидно, что диагональные элементы не должны быть нулевыми, т.к. мы на них делим), данная процедура сходится к истинному решению. Эта гимнастика известна в литературе под названием метода Якоби. Конечно же, существуют и другие методы численного решения систем линейных уравнений, причём значительно более мощные, например, метод сопряжённых градиентов, но, пожалуй, метод Якоби является одним из самых простых.

Видео:11 1 Метод наименьших квадратов ВведениеСкачать

Пример 3 ещё раз, но уже с другой стороны

А теперь давайте ещё раз внимательно посмотрим на основной цикл из примера 3:

Я стартовал с какого-то начального вектора x, и тысячу раз его обновляю, причём процедура обновления подозрительно похожа на метод Якоби! Давайте выпишем эту систему уравнений в явном виде:

Потратьте немного времени, убедитесь, что каждая итерация в моём питоновском коде — это строго одно обновление метода Якоби для этой системы уравнений. Значения x[0], x[18] и x[31] у меня зафиксированы, соответственно, в набор переменных они не входят, поэтому они перенесены в правую часть.

Итого, все уравнения в нашей системе выглядят как — x[i-1] + 2 x[i] — x[i+1] = 0. Это выражение не что иное, как обычные конечные разности для второй производной. То есть, наша система уравнений нам просто-напросто предписывает, что вторая производная должна быть везде равна нулю (ну, кроме как в точке x[18]). Помните, я говорил, что вполне очевидно, что итерации должны сойтись к линейным рампам? Так именно поэтому, у линейной функции вторая производная нулевая.

А вы знаете, что мы с вами только что решили задачу Дирихле для уравнения Лапласа?

Кстати, внимательный читатель должен был бы заметить, что, строго говоря, у меня в коде системы линейных уравнений решаются не методом Якоби, но методом Гаусса-Зейделя, который является своебразной оптимизацией метода Якоби:

Видео:Метод наименьших квадратов. Квадратичная аппроксимацияСкачать

Пример 4: уравнение Пуассона

А давайте мы самую малость изменим третий пример: каждая ячейка помещается не просто в центр масс соседних ячеек, но в центр масс плюс некая (произвольная) константа:

В прошлом примере мы выяснили, что помещение в центр масс — это дискретизация оператора Лапласа (в нашем случае второй производной). То есть, теперь мы решаем систему уравнений, которая говорит, что наш сигнал должен иметь некую постоянную вторую производную. Вторая производная — это кривизна поверхности; таким образом, решением нашей системы должна стать кусочно-квадратичная функция. Проверим на дискретизации в 32 сэмпла:

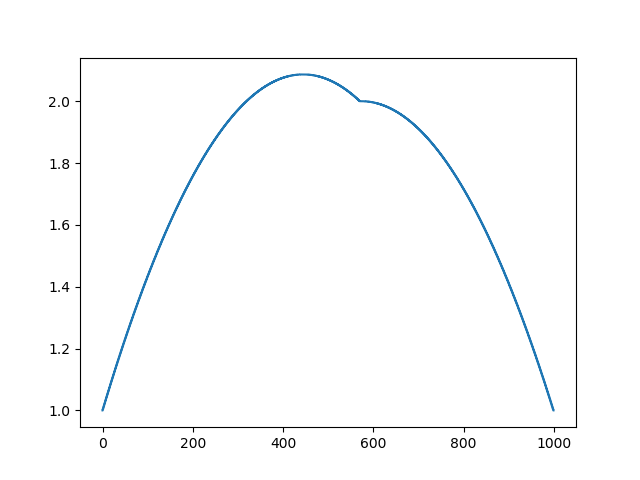
При длине массива в 32 элемента наша система сходится к решению за пару сотен итераций. А что будет, если мы попробуем массив в 128 элементов? Тут всё гораздо печальнее, количество итераций нужно уже исчислять тысячами:

Метод Гаусса-Зейделя крайне прост в программировании, но малоприменим для больших систем уравнений. Можно попытаться его ускорить, применяя, например, многосеточные методы. На словах это может звучать громоздко, но идея крайне примитивная: если мы хотим решение с разрешением в тысячу элементов, то можно для начала решить с десятью элементами, получив грубую аппроксимацию, затем удвоить разрешение, решить ещё раз, и так далее, пока не достигнем нужного результата. На практике это выглядит следующим образом:

А можно не выпендриваться, и использовать настоящие солверы систем уравнений. Вот я решаю этот же пример, построив матрицу A и столбец b, затем решив матричное уравнение Ax=b:

А вот так выглядит результат работы этой программы, заметим, что решение получилось мгновенно:

Таким образом, действительно, наша функция кусочно-квадратичная (вторая производная равна константе). В первом примере мы задали нулевую вторую производную, в третьем ненулевую, но везде одинаковую. А что было во втором примере? Мы решили дискретное уравнение Пуассона, задав кривизну поверхности. Напоминаю, что произошло: мы посчитали кривизну входящей поверхности. Если мы решим задачу Пуассона, задав кривизну поверхности на выходе равной кривизне поверхности на входе (const=1), то ничего не изменится. Усиление характеристических черт лица происходит, когда мы просто увеличиваем кривизну (const=2.1). А если const Скрытый текст

Это результат по умолчанию, рыжий Ленин — это начальные данные, голубая кривая — это их эволюция, в бесконечности результат сойдётся в точку:

А вот результат с коэффицентом 2.:

Домашнее задание: почему во втором случае Ленин сначала превращается в Дзержинского, а затем снова сходится к Ленину же, но большего размера?

Видео:Неоднородные системы линейных уравненийСкачать

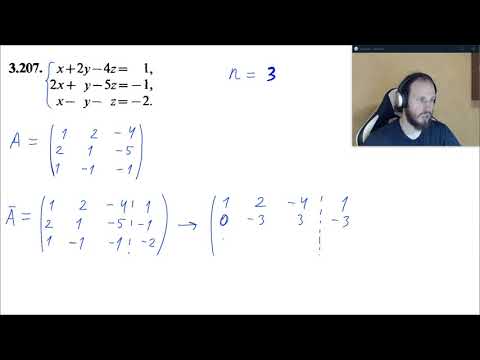
Заключение

Очень много задач обработки данных, в частности, геометрии, могут формулироваться как решение системы линейных уравнений. В данной статье я не рассказал, как строить эти системы, моей целью было лишь показать, что это возможно. Темой следующей статьи будет уже не «почему», но «как», и какие солверы потом использовать.

Кстати, а ведь в названии статьи присутствуют наименьшие квадраты. Увидели ли вы их в тексте? Если нет, то это абсолютно не страшно, это именно ответ на вопрос «как?». Oставайтесь на линии, в следующей статье я покажу, где именно они прячутся, и как их модифицировать, чтобы получить доступ к крайне мощному инструменту обработки данных. Например, в десяток строк кода можно получить вот такое:

Видео:Математика без Ху!ни. Метод Гаусса.Скачать

МЕТОД НАИМЕНЬШИХ КВАДРАТОВ И ПРИБЛИЖЕННОЕ РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ В ЭКОНОМИЧЕСКИХ ЗАДАЧАХ

1 Глава 3 МЕТОД НАИМЕНЬШИХ КВАДРАТОВ И ПРИБЛИЖЕННОЕ РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ В ЭКОНОМИЧЕСКИХ ЗАДАЧАХ 3 Метод наименьших квадратов Метод наименьших квадратов (часто называемый МНК) обычно упоминается в двух контекстах Во-первых, широко известно его применение в регрессионном анализе как метода построения моделей на основе зашумленных экспериментальных данных При этом помимо собственно построения модели обычно осуществляется оценка погрешности, с которой были вычислены её параметры, иногда решаются и некоторые другие задачи Во-вторых, МНК часто применяется просто как метод аппроксимации, без какой-либо привязки к статистике При решении различных экономических задач мы часто сталкиваемся с необходимостью обработки массивов экспериментальных данных В частности, с необходимостью решения системы линейных уравнений (СЛУ) AX = B, () где A = (a j ) матрица размера m, X вектор-столбец из неизвестных, те X = ( ), а B вектор-столбец из m элементов, те B = (b b m ) Рассматриваемая СЛУ, как правило, несовместна, если в ней число уравнений превышает число неизвестных Поэтому говорить о ее точном решении невозможно Невязкой системы AX = B по -ой проекции относительно вектора X называется разность δ = ( a+ K+ a) b ( =, m) Определение Вектором невязки системы () относительно вектора называется вектор δ = ( AX B) 35

2 Ошибкой S(X) системы относительно вектора X называется квадрат длины (или нормы) вектора невязки, те сумма квадратов невязок по всем проекциям, те S( X) = δ + K + δm Отметим, что в евклидовом m-мерном точечном пространстве ошибка S() представляет собой квадрат расстояния между точками AX и B, где B = (b b m ) и ( AX ) = ( a + K+ a, K, a + K + a m m ) Если X = (, K, ) точное решение системы (), то векторстолбец B есть линейная комбинация столбцов A,, A матрицы A, где = (,, m),, = (,, ) A a K a K A a K a m Если X точное решение системы (), то вектор-столбец B является линейной комбинацией столбцов A,, A матрицы A, где = (,, m),, = (,, ) A a K a K A a K a m В качестве приближенного решения системы () выбирается такая точка X, для которой ошибка S(X) имеет наименьшее значение Наилучшее приближенное решение X* системы () совпадает с точным решением системы: 36 ( A, A) + K + ( A, A) = ( A, B), KK KK KK ( A, A) + K + ( A, A) = ( A, B) В матричной форме эта система записывается в виде A AX ( ) = A B () Определение СЛУ () (или ( )) называется системой нормальных уравнений для системы () Теорема Если столбцы матрицы A линейно независимы, то система нормальных уравнений () имеет единственное решение X*, и это решение дает наименьшее значение функции S( X) = AX B суммы квадратов ошибок по проекциям СЛУ () Доказательство этой теоремы можно найти в [0]

3 δ кр Приближенным решением системы () называется произвольный -мерный вектор X, если при этом ошибка S(X) не превосходит заранее заданного критического значения δ кр Псевдорешением системы () называется вектор X, в котором ошибка S(X) системы принимает свое наименьшее значение Если ошибка S(X) при этом не превосходит заданной точности, то псевдорешение является наилучшим приближенным решением системы () Теорема гарантирует существование и единственность псевдорешения системы () в достаточно общем случае Тот факт, что ошибка S(X) представляет собой сумму квадратов ошибок по всем проекциям объясняет название метода наименьших квадратов 4B3 Применение метода наименьших квадратов На практике метод наименьших квадратов (МНК) часто используется при анализе статистических данных для выявления функциональной зависимости между несколькими наблюдаемыми величинами Ограничимся случаем двух величин и y, между которыми предполагается наличие функциональной связи y = P(), где P ( ) = p + p+ p + K+ p многочлен степени k 0 При этом мы считаем, что число наблюдений, те пар (, y)( =,, K, ) экспериментальных данных не менее, чем число k + неизвестных коэффициентов многочлена В этом случае при решении СЛУ p + p + + p = y K K K K k p0 + p + K + pk = y k 0 K k, используется метод наименьших квадратов Матрица коэффициентов системы при этом имеет вид k K k K A = K K K K k K k k 37

4 Пример Пусть произведено взвешиваний одного и того же драгоценного камня Найти вес камня, используя метод наименьших квадратов 38

5 Решение Исходная система имеет уравнений с одним неизвестным, где вес камня: = b, K, = b или в матричном виде b b X = K K b При система, как правило, несовместна и A = (,, K,) Система принимает вид = b + K + b Отсюда получаем b + K+ b = псевдорешение исходной системы Если между величинами существует линейная зависимость y = α + β и проведено измерений (, y ), где =,, то МНК позволяет получить приближенную линейную зависимость y = α * + β * Пусть известно, что y = α + β и проведено измерений (, y ), где =,, K, Тогда для определения параметров α и β имеем СЛУ: α + β = y, K K K, α + β = y или в матричном виде y α K K = β K (3) y 39

6 Система нормальных уравнений для (3) принимает вид α + β = y α + β = y Решая систему (4), найдем y y β* = Если ввести обозначения =, y = y средние значения наблюдаемых величин, то первое уравнение примет вид α + β = y С учетом обозначений средних величин можно теперь записать решение системы (4) в виде формул * y y β =, ( ) α* = y β * Таким образом, в случае линейной зависимости МНК дает линейное уравнение y = α * + β *, где коэффициенты α* и β* находятся по формулам (5) Отметим, что в случае квадратичной (параболической) зависимости y= α + β+ γ система нормальных уравнений () прини- мает вид α + β + γ = y, 3 α + β + γ = y, 3 4 α + β + γ = y (4) (5) (6) 40

7 5B33 Приближенное решение систем линейных уравнений и обусловленность матриц Когда мы занимаемся задачей сглаживания экспериментальных данных, мы имеем дело, как правило, с несовместной СЛУ, в которой число неизвестных меньше числа уравнений Для решения такой задачи часто применятся МНК В результате мы получаем наилучшее приближенное решение исходной несовместной СЛУ Следует отметить, что, имея дело с экспериментальными данными, мы имеем дело с приближенными числами Поэтому в такой задаче важно уметь оценить, как сильно изменится решение исходной СЛУ, если каким-то образом изменится вектор-столбец свободных членов или исходная матрица коэффициентов СЛУ Для такой оценки вводится число обусловленности квадратной невырожденной матрицы Отметим, что при использовании МНК решается система нормальных уравнений (), матрица которой квадратная, симметрическая и невырожденная Определение Нормой матрицы A называется такое число A, для которого верны следующие свойства: ) A 0( A 0) > ; ) A + B A + B ; 3) λ A = λ A ; 4) AB A B ; 5) A A ; где A, B матрицы, вектор, λ число Примерами норм матрицы A = ( a j ) являются следующие числа: A где, =, j a j ; A = a, j j ; A 3 A = sup, 0 A введенные ранее нормы (длины) векторов и A Норма матрицы A называется согласованной с нормой вектора, A если A = sup 0 Всем перечисленным требованиям удовлетворяет, например, aj, A где a j элементы матрицы A, или aj, или sup,, j где,, j 0 A введенные ранее нормы (длины) векторов и A 4

8 Для согласованной нормы и единичной матрицы E, очевидно, имеем E= для любого вектора линейного пространства L, и, следовательно, E = Рассмотрим СЛУ A= b, где A квадратная матрица порядка, de A 0, b 0 В этом случае система имеет единственное ненулевое решение На практике при решении СЛУ вычисления производятся с округлениями, те неточно Погрешность вычислений при этом часто можно интерпретировать как погрешность правой части Рассмотрим, наряду с СЛУ A= b, систему A( + ) = b+ δ b, где δ b 0 погрешность правой части, а погрешность решения Из двух последних равенств вытекает Aδ = δ b и = A δb В силу свойств нормы матрицы имеем, что b A и A δb Перемножая эти неравенства, получим b δ A A δ b Разделив последнее неравенство на b 0, имеем A A δb Определение Если A невырожденная квадратная матрица, то число ca ( ) = A A называется числом обусловленности матрицы A С учетом определения числа обусловленности последнее неравенство можно переписать в виде δb ca ( ) (7) b Неравенство (7) дает оценку относительной погрешности вектора решения в зависимости от вектора-столбца свободных членов b Отметим, что число обусловленности так же важно, если матрица A имеет погрешность, а вектор b известен точно В самом деле, решим систему ( A + δ A)( + ) = b Тогда + δ= ( A+ δa) b равенства второе, получим 4 δ= (( A+ δa) A ) b и из b = A b Вычитая из первого Введем обозначение B = A+ δ A и используем тождество A ( A B) B = A AB A BB = EB A E = B A

9 Далее имеем = ( B A ) b = ( A ( A B) B ) b = = A δ AA ( + δa) ) b= A δa ( + δ) Отсюда A δa + δ, те A δ A Домножив и разделив правую часть последнего неравенства на A, + получим δ A ca ( ) + A, (8) те неравенство, аналогичное неравенству (7) Для вычисления евклидовой нормы матрицы и ее числа обусловленности используют две следующие теоремы Теорема Евклидова норма матрицы A, согласованная с евклидовой нормой векторов, равна A = ma λ ( AA ) (9) Для симметрической матрицы формула (9) упрощается A = ma λ ( A) (0) Здесь через λ ( B) обозначены собственные значения матрицы B Теорема Если матрица A симметричная, то число обусловленности матрицы можно вычислить по формуле ma λ ca ( ) = () m λ j j Если матрица A не является симметричной, то число обусловленности равно ca ( ) = caa ( ) () 43

10 6BПримеры Пусть имеются следующие экспериментальные данные о цене нефти и индексе нефтяных компаний: 7,30 7,08 8,30 8,80 9,0 8,50 y Считая, что между величинами и y существует линейная зависимость, применяя метод наименьших квадратов (МНК), найти эту зависимость Решение Найдем необходимые для расчетов средние величины, yy,, Запишем результаты этих вычислений в виде таблицы y y 7, ,36 98,5984 7, ,70 90, , ,00 334, , ,00 353,44 5 9, ,00 368,64 6 8, ,00 34,5 09, ,06 988,509 s 8, ,5 33,40 Используя формулы (5), получим β*,35, α* 37,9 По экспериментальным данным,0,5,0,5 3,0 y 0,50 0,30 0,5 0,8 0, построить с помощью МНК линейную зависимость y от Сравнить полученную зависимость с зависимостью y = Решение Найдем необходимые для расчетов средние величины, yy,, Запишем результаты этих вычислений в виде таблицы 44

11 y y,0 0,50 0,50,0,5 0,30 0,45,5 3,0 0,5 0,50 4,0 4,5 0,8 0,45 6,5 5 3,0 0, 0,36 9,0 0,35,6,5 s 0,7 0,45 4,5 Используя формулы (5), получим β* 0,76; α* 0,6 Следовательно, НМК дает зависимость y = 0,6 0,76 Сравним значения S = ( f( ) y ) для найденной линейной и предложенной экспоненциальной зависимости Запишем промежуточные результаты этих вычислений в виде таблицы y ( y ) (0,6 0,76 y ),0 0,50 0,5 0 0,0096,5 0,30 0,3536 0, , ,0 0,5 0,5 0 0,0004 4,5 0,8 0,768 0, , ,0 0, 0,5 0, , ,35 0, ,00736 Итак, результаты вычислений дают S лин = 0,00736, а S эксп = 0,00908 Ответ: S лин = 0,00736, S эксп = 0,00908; экспоненциальная зависимость лучше, чем линейная отражает экспериментальные данные 3 Имеются следующие данные о расходах на производство и доходах от реализации в условных единицах,5,0,5 3,0 y,4, 3,6 5, 8,0 Найти квадратичную зависимость МНК y= α + β+ γ с помощью 45

12 Решение Найдем необходимые для расчетов суммы 3 4. y, y, y Результаты вычислений приведем в таблице y 3 4 y y,0,4,0,0,0,4,4,5,,5 3,375 5,065 3,3 4,95 3,0 3,6 4,0 8,0 6,0 7, 4,4 4,5 5, 6,5 5,65 39,065,75 3, ,0 8,0 9,0 7,0 8,0 4,0 7,0 0 0,3,5 55,0 4,5 48,65 4,65 В результате получим систему уравнений вида 5α + 0β +, 5γ = 0, 3, 0α +, 5β + 55γ = 48, 65,, 5α + 55β + 4,5γ = 4, 65 Решив систему методом исключения неизвестных, получим приближенный ответ α,9; β,696; γ,9 Ответ: α,9; β,696; γ,9 4 Найдите число обусловленности симметричной матрицы A и оцените относительную погрешность решения системы A( + ) = b+ δb, если 3 4 0, A = 3, b =, δb = 0, , Решение Находим собственные значения матрицы A: λ 3 A λe = λ 3 = ( λ )( λ 4λ 5) = λ 46

13 Корни характеристического уравнения равны λ = ; λ = + 9 6,36; λ 3 = 9,36 Далее, ma λ = + 9, m λ =, ca= ( ) + 9, b = 6, δ b = 0,5 Отсюда по формуле (7) имеем 0,5 ( + 9) = 0,05( + 9) 0,05 6,36 0,59 6 Ответ: ca= ( ) + 9, 0,59 5 Найдите число обусловленности матрицы A и оцените относительную погрешность решения системы A( + ) = b+ δb, если 0 0 0, A = 3, b =, δb = 0, , Решение 3 Вычисляем AA= Находим собственные зна- 3 чения матрицы A A: λ 3 3 AA λe= 3 3 λ 3 = λ + 7λ 9λ+ 3= 0 3 λ Корни характеристического уравнения равны λ = ; λ = ,45; λ 3 = 3 6 0,55 Далее, ma λ = 3 + 6, m λ = 3 6, 3+ 6 caa ( ) = = , ca ( ) = = 3 + 3,46 47

14 4 Далее, b = 4, δ b = Отсюда по формуле (7) имеем, 0 что 3,46 0, 0,35 Ответ: ca= ( ) 3 + 3,46, 0,35 6 Оцените относительную погрешность решения системы ( A + δ A)( + ) = b, если 3 0, 0 0,05 A = 3 и δ A = 0 0, 0, 3 3 0,05 0, 0, 4 Решение В примере 5 уже было вычислено число обусловленности ca ( ) = + 9 = A Находим теперь собственные значения матрицы δ A: 0, λ 0 0,05 δa λe = 0 0, λ 0, = 0, 05 0, 0, 4 λ = (0, λ)( λ 0, 6λ + 0, 0675) = 0 Решая полученное характеристическое уравнение, получим собственные значения матрицы δ A: λ = 0, ; λ = 0, 45; λ = 0,5 Используя формулу (8), получим оценку относительной погрешности решения системы: 0,45 ( + 9) = 0,45 + ( + 9) Ответ: 0,45 + Ряд наблюдений значений некоторого показателя, упорядоченный в зависимости от значений другого показателя, называют динамическим или временным рядом Другими словами динамический ряд есть последовательность пар (, y ), в которой значения показателя упорядочены по возрастанию 48

15 Как правило, одним из показателей является время, которое часто обозначается условными моментами времени,,3, Отрезок динамического ряда, на котором значения показателя y изменяются монотонно, называется трендом Заметим, что систему нормальных уравнений можно упростить и уменьшить абсолютные значения величин, если перенести начало координат в середину динамического ряда Если до переноса начала координат равно,,3,, то после переноса получим: ) для четного числа членов равно K, 5, 3. 3,5, K, ) для нечетного числа членов равно K, 3. 0. 3, K В этом случае формулы (5) упрощаются и коэффициенты линейного тренда могут быть вычислены по более простым формулам: y α = y ; β = (3) В случае параболического тренда в этом случае тоже имеются достаточно простые формулы для коэффициентов α, β и γ, а именно: y α = ( y y) 4 ( ) β = y, ( y y) γ = (4) 4 ( ) 7 По данным ежемесячных объемов выпуска продукции фирмы за 8 месяцев: y рассчитать: а) коэффициенты α и β линейного тренда y = α + β и прогноз на месяц вперед; б) коэффициенты α, β и γ параболического тренда y= α + β+ γ и прогноз на месяц вперед Решение Для расчета коэффициентов линейного и параболического трендов воспользуемся выражениями, полученными из системы, 49

16 нормальных уравнений Перенесем начало координат (ί’) Необходимые вычисления занесем в таблицу Линейный тренд y ( ) y Итого Вычислим коэффициенты линейного тренда по формулам: Α = Σ y / = 4 634/8 = 3079,5; y 8066 β = = 48,0 (‘) 68 Таким образом, величина среднего уровня ряда при = 0 составляет 3079,5, среднемесячное уменьшение выпуска продукции составляет 48,0 Уравнение линейного тренда: y = 3079,5 48,0 ‘ Прогноз на 9-й месяц составит: y = 3079,5 48,0 9 = 647,6 Параболический тренд y (‘) y ‘ 3 (‘) 4 (‘) y (‘) Итого Вычислим коэффициенты параболического тренда по формулам (334): α = 3077,05; β = 48,0; γ = 0,05 Прогноз на 9-й месяц: y = , ,05 8 = 653,47 50

17 Ответ: Уравнение параболического тренда: y= 3077,05 48,0 ‘ + 0,05( ‘) Прогноз на 9-й месяц: y = 653, 47 8 В таблице приведены данные о доходности и рыночном индексе за 0 лет Предполагая зависимость между доходностью r и рыночным индексом r линейной, найти эту зависимость r = α + βr вид I Год r 0,8, 6,, 0,4 4,9 7,9,8 0,0 4,9 r 6,6 0,,5 3,9 0,4 8,4,6 0, 0,7 4,5 I Решение Система нормальных уравнений линейной зависимости имеет 0α + 30β =, 8, 30α + 63, 3β =, 696 Решая систему, получим α = 0,4, β = 0,79 Ответ: r = 0,4 + 0,79r I 7BУпражнения и тестовые вопросы 3 Что такое вектор невязки для несовместной СЛУ относительно вектора X? Найти вектор невязки 3+ 4y =, для СЛУ 5+ 3y = 3, относительно вектора X = (,3; ) + 5y = 3 Как связаны между собой вектор невязки и ошибка несовместной СЛУ относительно вектора X? Пусть вектор невязки несовместной СЛУ относительно вектора X равен δ = (0,3;0,;0,;0,;0,) Чему равна ошибка S(X) этой СЛУ относительно вектора X? 33 Что такое система нормальных уравнений для несовместной СЛУ? Написать систему нормальных уравнений несовместной 3+ 5y = 0, СЛУ 5+ 3y =, + 7y = I 5

18 34 Что называется числом обусловленности квадратной невырожденной матрицы? Указать формулы вычисления числа обусловленности матрицы в евклидовой норме в случае симметричной матрицы и в общем случае 35 Найти наилучшее приближенное решение несовместной СЛУ с помощью метода наименьших квадратов (МНК) + 3y = 8, 4+ 5y =, 5+ 3y = 9, 3+ 7y = 4 В ответе с точностью до 0,0 указать решение, вектор невязки δ, и длину вектора невязки 36 Пусть цена на товар (усле) и y объем продаж товара y Предполагая, что между и y существует линейная зависимость y = α + β, найти эту зависимость с помощью МНК Вычислить вектор невязки δ и ошибку системы S 37 По экспериментальным данным с помощью МНК постройте линейную зависимость y = α + β Сравните эту зависимость с зависимостью y= ,3, сопоставляя их ошибки S лин и S кв y В результате исследования зависимости между сроком эксплуатации автомобиля и расходами на его ремонт получены следующие данные: 5, лет S, тыс руб Найдите а) линейную зависимость S = α + β стоимости ремонта автомобиля от срока его эксплуатации;

19 б) предполагаемую величину затрат на 0-ый год его эксплуатации 53

Видео:Неоднородная система линейных уравненийСкачать

Решение систем линейных уравнений методом наименьших квадратов

Пусть дана действительная или комплексная система линейных уравнений

в матричной форме имеющая вид

Если система (8.70) описывает реальный физический процесс, но оказывается несовместной, то естественно ввести коррективы в математическую модель и, в частности, изменить трактовку понятия «решение». Например, часто возникает задача найти такие значения неизвестных ад, Х2, . х_п, при которых функция

где х = (ад, ад. х_п) т , принимает наименьшее значение. Этот подход к понятию решения линейной системы составляет суть метода наименьших квадратов. При этом найденный набор значений х = (ад, ад, . х_п) Т называют псевдорешением или обобщенным решением системы. Очевидно, что если система Ах = b совместна, то ее псевдорешение представляет собой обычное решение, а любое решение системы можно искать как ее псевдорешение.

Описанный подход к понятию решения линейной системы объясняется следующими соображениями. Пусть некоторый процесс описывается некоторым набором величин од, 2 имела наименьшее значение, длина вектора z должна быть минимальной. Это возможно, лишь когда в равенстве Ах + z = Ъ вектор Ах = А х + А^ Х2 +. + +А_пх_п является ортогональной проекцией (см. разд. 8.5) вектора b на пространство Ь(А) столбцов А, А2, . А_п матрицы А, а вектор z — ортогональной составляющей вектора Ъ. Поэтому вектор 2 должен быть ортогональным к каждому вектору-столбцу Aj матрицы А. Следовательно, (2, А,) = 0, j = 1, 2. п. В матричной форме это означает, что A* z = 0. Отсюда, умножив равенство А х + z = b слева на матрицу А*, получим систему

В действительном (вещественном) случае к системе (8.73) можно прийти также используя методы математического анализа, а именно, приравняв к нулю дифференциал

функции

или, что то же самое, приравняв к нулю первые частные производные ПО Х, Х2, . х_п функции F<x).

Примечание. При вычислении дифференциала dF(x) использовано то обстоятельство, что вещественное выражение (Ax — b)* A dx, являясь матрицей первого порядка, не меняется при транспонировании и комплексном сопряжении и потому совпадает с выражением dx* А* (А х — Ь).

Систему А* Ах = А* b называют системой нормальных уравнений. Ее матрица А* А квадратная п-го порядка. Это матрица Грама системы столбцов матрицы А.

Теорема 8.40. Система А* Ах = А* b всегда совместна, причем ее решения, и только они, являются псевдорешениями системы Ах = Ь.

О Сначала убедимся в совместности системы нормальных уравнений. Для этого докажем, что вектор .то = А + Ъ, где А + — псев- дообратная к А матрица, является решением этой системы. С этой целью возьмем какое-нибудь скелетное разложение А = В С матрицы А. Тогда А* = С* В*, Л+ = С* (СС*)- 1 (В* Б)» 1 В* и

Следовательно, Хо = А + b — решение системы нормальных уравнений, а эта система совместная.

В совместности системы нормальных уравнений можно убедиться и следующим образом. Представим столбец b в виде Ь = Ь _<]+ /Д, где

А-, — столбцы матрицы А, Ь 1 — — ортогональная составляющая вектора Ъ. Тогда

Таким образом, система нормальных уравнений равносильна системе А* Ах = А* Ьо, а последняя всегда совместная, поскольку при х = (ki,k₂, . k_n) T

Перейдем к доказательству второй части утверждения теоремы. Пусть х — решение системы нормальных уравнений А* Ах = А* Ь. Эта система равносильна системе А* (А х — Ь) = 0, означающей, что каждый столбец матрицы А ортогонален столбцу г = Ах—b. Следовательно, столбец А х является проекцией вектора b на подпространство Ь(А), порожденное столбцами матрицы А, а вектор х есть псевдорешение системы Ах = Ь.

Эти рассуждения можно провести и в обратном порядке (см. вывод системы нормальных уравнений). Тогда придем к заключению, что псевдорешения системы Ах = b являются решениями системы нормальных уравнений. ?

Следствис8.6. Общее псевдорешение системы Ах = b представимо в виде

где .то — какое-либо частное решение системы А* Ах — А* 6, т.е. какое- либо частное псевдорешение системы А х = 6, а т₀б_Щ — общее решение однородной системы А* А х = 0.

Следствие 8.7. Система А* Ах = А* b имеет единственное решение, если столбцы матрицы А линейно независимы, и бесконечное множество решений, если столбцы матрицы А линейно зависимы.

О Определитель системы А* Ах = А* b есть определитель матрицы Грама системы столбцов матрицы А. Этот определитель отличен от нуля тогда и только тогда, когда столбцы матрицы А линейно независимы. В то же время это условие означает, что система А* Ах = А* b имеет единственное решение. ?

Еще и еще раз подчеркнем, что решения х системы А* Ах = А* b нормальных уравнений, и только они, являются псевдорешениями системы Ах = Ь. Причем, при таких х, и только при них, вектор Ах = Ах 1 + А2Х2 + . + А_пх_п является (см. раздел 8.5) ортогональной проекцией вектора b на подпространство Ь(А), порожденное столбцами А, А2, . А_п матрицы А, а вектор z = Ах — b — ортогональной составляющей вектора Ъ.

Итак, чтобы решить систему Ах = b методом наименьших квадратов, нужно найти общее решение системы А* Ах = А* b и, если требуется, из множества решений выделить нормальное решение, т.е. то, которое имеет наименьшую длину.

Пример 8.36. Для системы

найти общее и нормальное псевдорешения.

Решение. Составим систему А* Ах — А* Ъ нормальных уравнений, которая в данном случае имеет вид:

Решив эту систему, найдем общее псевдорешение Теперь составим функцию

Из равенства нулю ее производной по Х найдем ж 4 = 1, при котором из общего псевдорешения х получается нормальное псевдорешение х° = (3, —5, 3,1) т .

Если для выделения нормального псевдорешения применить второй способ, то сначала нужно построить какую-либо ФСР однородной системы Ах = 0. В данном случае ФСР состоят из одного решения. Одна из этих ФСР состоит из решения X = ( — 1, —1, —1,1) т . Далее из соотношения ортогональности

векторов X и х найдем значение Х4 = 1, при котором из общего псевдорешения х выделяется нормальное псевдорешение х° = (3, —5,3,

Пример 8.37. Найти многочлен p(t) = х + X2t—x^t 2 , с наименьшей квадратичной погрешностью приближающий функцию /(?), которая задана таблицей

🔥 Видео

Система уравнений. Метод алгебраического сложенияСкачать

Суть метода наименьших квадратов с примерами. Основы эконометрики в RСкачать

Решение системы уравнений методом ГауссаСкачать

Система линейных уравнений. Общее решение. Метод ГауссаСкачать

Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Решение систем линейных уравнений, урок 4/5. Метод ГауссаСкачать

Решение систем линейных алгебраических уравнений методом Крамера.Скачать

Метод Гаусса решения систем линейных уравненийСкачать

Метод наименьших квадратов. Регрессионный анализ.Скачать

Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать