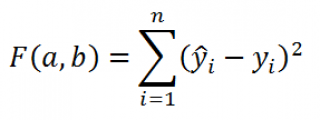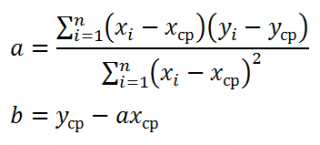Поможем написать любую работу на аналогичную тему
Сущность метода наименьших квадратов заключается в отыскании параметров модели тренда, которая лучше всего описывает тенденцию развития какого-либо случайного явления во времени или в пространстве (тренд – это линия, которая и характеризует тенденцию этого развития). Задача метода наименьших квадратов (МНК) сводится к нахождению не просто какой-то модели тренда, а к нахождению лучшей или оптимальной модели. Эта модель будет оптимальной, если сумма квадратических отклонений между наблюдаемыми фактическими величинами и соответствующими им расчетными величинами тренда будет минимальной (наименьшей):

где 
и соответствующей ей расчетной величиной тренда,



МНК самостоятельно применяется довольно редко. Как правило, чаще всего его используют лишь в качестве необходимого технического приема при корреляционных исследованиях. Следует помнить, что информационной основой МНК может быть только достоверный статистический ряд, причем число наблюдений не должно быть меньше 4-х, иначе, сглаживающие процедуры МНК могут потерять здравый смысл.
Инструментарий МНК сводится к следующим процедурам:
Первая процедура. Выясняется, существует ли вообще какая-либо тенденция изменения результативного признака при изменении выбранного фактора-аргумента, или другими словами, есть ли связь между «у» и «х».
Вторая процедура. Определяется, какая линия (траектория) способна лучше всего описать или охарактеризовать эту тенденцию.
Третья процедура. Рассчитываются параметры регрессионного уравнения, характеризующего данную линию, или другими словами, определяется аналитическая формула, описывающая лучшую модель тренда.
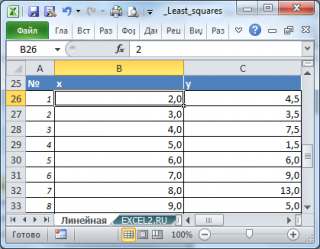
Пример. Допустим, мы имеем информацию о средней урожайности подсолнечника по исследуемому хозяйству (табл. 9.1).
Поскольку уровень технологии при производстве подсолнечника в нашей стране за последние 10 лет практически не изменился, значит, по всей видимости, колебания урожайности в анализируемый период очень сильно зависели от колебания погодно-климатических условий. Действительно ли это так?
Первая процедура МНК. Проверяется гипотеза о существовании тенденции изменения урожайности подсолнечника в зависимости от изменения погодно-климатических условий за анализируемые 10 лет.
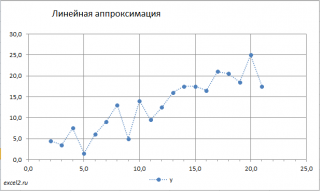
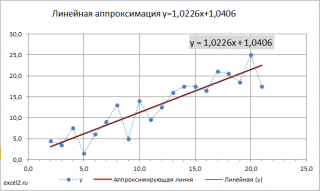
В данном примере за «y» целесообразно принять урожайность подсолнечника, а за «x» – номер наблюдаемого года в анализируемом периоде. Проверку гипотезы о существовании какой-либо взаимосвязи между «x» и «y» можно выполнить двумя способами: вручную и при помощи компьютерных программ. Конечно, при наличии компьютерной техники данная проблема решается сама собой. Но, чтобы лучше понять инструментарий МНК целесообразно выполнить проверку гипотезы о существовании связи между «x» и «y» вручную, когда под рукой находятся только ручка и обыкновенный калькулятор. В таких случаях гипотезу о существовании тенденции лучше всего проверить визуальным способом по расположению графического изображения анализируемого ряда динамики — корреляционного поля:
Корреляционное поле в нашем примере расположено вокруг медленно возрастающей линии. Это уже само по себе говорит о существовании определенной тенденции в изменении урожайности подсолнечника. Нельзя говорить о наличии какой-либо тенденции лишь тогда, когда корреляционное поле похоже на круг, окружность, строго вертикальное или строго горизонтальное облако, или же состоит из хаотично разбросанных точек. Во всех остальных случаях следует подтвердить гипотезу о существовании взаимосвязи между «x» и «y», и продолжить исследования.
Вторая процедура МНК. Определяется, какая линия (траектория) способна лучше всего описать или охарактеризовать тенденцию изменения урожайности подсолнечника за анализируемый период.
При наличии компьютерной техники подбор оптимального тренда происходит автоматически. При «ручной» обработке выбор оптимальной функции осуществляется, как правило, визуальным способом – по расположению корреляционного поля. То есть, по виду графика подбирается уравнение линии, которая лучше всего подходит к эмпирическому тренду (к фактической траектории).
Как известно, в природе существует огромное разнообразие функциональных зависимостей, поэтому визуальным способом проанализировать даже незначительную их часть — крайне затруднительно. К счастью, в реальной экономической практике большинство взаимосвязей достаточно точно могут быть описаны или параболой, или гиперболой, или же прямой линией. В связи с этим, при «ручном» варианте подбора лучшей функции, можно ограничиться только этими тремя моделями.
Прямая:
Гипербола:
Парабола второго порядка: 
Нетрудно заметить, что в нашем примере лучше всего тенденцию изменения урожайности подсолнечника за анализируемые 10 лет характеризует прямая линия, поэтому уравнением регрессии будет уравнение прямой.
Третья процедура. Рассчитываются параметры регрессионного уравнения, характеризующего данную линию, или другими словами, определяется аналитическая формула, описывающая лучшую модель тренда.
Нахождение значений параметров уравнения регрессии, в нашем случае параметров 


Эта система уравнений довольно легко решается методом Гаусса. Напомним, что в результате решения, в нашем примере, находятся значения параметров 

В линейном уравнении параметр 







Приведем также системы нормальных уравнений для отыскивания параметров нелинейных уравнений.
- МНК: Метод Наименьших Квадратов в EXCEL
- Линейная зависимость
- Инструмент диаграммы Линия тренда
- Метод наименьших квадратов (МНК), линейная аппроксимация
- Постановка задачи на конкретном примере
- Наборы данных
- Графическая иллюстрация метода наименьших квадратов (мнк).
- Сглаживание ряда методом наименьших квадратов
- 🔍 Видео
Видео:Метод наименьших квадратов (МНК)Скачать
МНК: Метод Наименьших Квадратов в EXCEL
history 11 ноября 2018 г.
- Группы статей
- Статистический анализ
Метод наименьших квадратов (МНК) основан на минимизации суммы квадратов отклонений выбранной функции от исследуемых данных. В этой статье аппроксимируем имеющиеся данные с помощью линейной функции y = a x + b .
Метод наименьших квадратов (англ. Ordinary Least Squares , OLS ) является одним из базовых методов регрессионного анализа в части оценки неизвестных параметров регрессионных моделей по выборочным данным.
Рассмотрим приближение функциями, зависящими только от одной переменной:
Примечание : Случаи приближения полиномом с 3-й до 6-й степени рассмотрены в этой статье. Приближение тригонометрическим полиномом рассмотрено здесь.
Видео:Метод наименьших квадратов. Линейная аппроксимацияСкачать

Линейная зависимость
Нас интересует связь 2-х переменных х и y . Имеется предположение, что y зависит от х по линейному закону y = ax + b . Чтобы определить параметры этой взаимосвязи исследователь провел наблюдения: для каждого значения х i произведено измерение y i (см. файл примера ). Соответственно, пусть имеется 20 пар значений (х i ; y i ).
Для наглядности рекомендуется построить диаграмму рассеяния.
Примечание: Если шаг изменения по х постоянен, то для построения диаграммы рассеяния можно использовать тип График , если нет, то необходимо использовать тип диаграммы Точечная .
Из диаграммы очевидно, что связь между переменными близка к линейной. Чтобы понять какая из множества прямых линий наиболее «правильно» описывает зависимость между переменными, необходимо определить критерий, по которому будут сравниваться линии.
В качестве такого критерия используем выражение:
Вышеуказанное выражение представляет собой сумму квадратов расстояний между наблюденными значениями y i и ŷ i и часто обозначается как SSE ( Sum of Squared Errors ( Residuals ), сумма квадратов ошибок (остатков) ) .
Метод наименьших квадратов заключается в подборе такой линии ŷ = ax + b , для которой вышеуказанное выражение принимает минимальное значение.
Примечание: Любая линия в двухмерном пространстве однозначно определяется значениями 2-х параметров: a (наклон) и b (сдвиг).
Считается, что чем меньше сумма квадратов расстояний, тем соответствующая линия лучше аппроксимирует имеющиеся данные и может быть в дальнейшем использована для прогнозирования значений y от переменной х. Понятно, что даже если в действительности никакой взаимосвязи между переменными нет или связь нелинейная, то МНК все равно подберет «наилучшую» линию. Таким образом, МНК ничего не говорит о наличии реальной взаимосвязи переменных, метод просто позволяет подобрать такие параметры функции a и b , для которых вышеуказанное выражение минимально.
Проделав не очень сложные математические операции (подробнее см. статью про квадратичную зависимость ), можно вычислить параметры a и b :
Как видно из формулы, параметр a представляет собой отношение ковариации и дисперсии , поэтому в MS EXCEL для вычисления параметра а можно использовать следующие формулы (см. файл примера лист Линейная ):
= КОВАР(B26:B45;C26:C45)/ ДИСП.Г(B26:B45) или
Также для вычисления параметра а можно использовать формулу = НАКЛОН(C26:C45;B26:B45) . Для параметра b используйте формулу = ОТРЕЗОК(C26:C45;B26:B45) .
И наконец, функция ЛИНЕЙН() позволяет вычислить сразу оба параметра. Для ввода формулы ЛИНЕЙН(C26:C45;B26:B45) необходимо выделить в строке 2 ячейки и нажать CTRL + SHIFT + ENTER (см. статью про формулы массива, возвращающими несколько значений ). В левой ячейке будет возвращено значение а , в правой – b .
Примечание : Чтобы не связываться с вводом формул массива потребуется дополнительно использовать функцию ИНДЕКС() . Формула = ИНДЕКС(ЛИНЕЙН(C26:C45;B26:B45);1) или просто = ЛИНЕЙН(C26:C45;B26:B45) вернет параметр, отвечающий за наклон линии, т.е. а . Формула = ИНДЕКС(ЛИНЕЙН(C26:C45;B26:B45);2) вернет параметр, отвечающий за пересечение линии с осью Y, т.е. b .
Вычислив параметры, на диаграмме рассеяния можно построить соответствующую линию.
Видео:Как работает метод наименьших квадратов? Душкин объяснитСкачать

Инструмент диаграммы Линия тренда
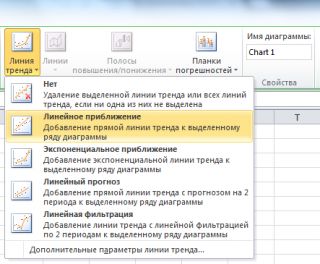
Еще одним способом построения прямой линии по методу наименьших квадратов является инструмент диаграммы Линия тренда . Для этого выделите диаграмму, в меню выберите вкладку Макет , в группе Анализ нажмите Линия тренда , затем Линейное приближение .
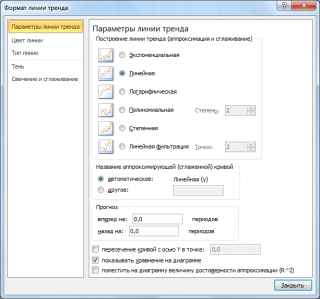
Поставив в диалоговом окне галочку в поле «показывать уравнение на диаграмме» можно убедиться, что найденные выше параметры совпадают со значениями на диаграмме.
Примечание : Для того, чтобы параметры совпадали необходимо, чтобы тип у диаграммы был Точечная, а не График . Дело в том, что при построении диаграммы График значения по оси Х не могут быть заданы пользователем (пользователь может указать только подписи, которые не влияют на расположение точек). Вместо значений Х используется последовательность 1; 2; 3; … (для нумерации категорий). Поэтому, если строить линию тренда на диаграмме типа График , то вместо фактических значений Х будут использованы значения этой последовательности, что приведет к неверному результату (если, конечно, фактические значения Х не совпадают с последовательностью 1; 2; 3; …).
СОВЕТ : Подробнее о построении диаграмм см. статьи Основы построения диаграмм и Основные типы диаграмм .
Видео:Метод наименьших квадратов. Квадратичная аппроксимацияСкачать

Метод наименьших квадратов (МНК), линейная аппроксимация
Видео:Пример решения задачи методом наименьших квадратовСкачать

Постановка задачи на конкретном примере
Предположим, имеются два показателя X и Y. Причем Y зависит от X. Так как МНК интересует нас с точки зрения регрессионного анализа (в Excel его методы реализуются с помощью встроенных функций), то стоит сразу же перейти к рассмотрению конкретной задачи.
Итак, пусть X — торговая площадь продовольственного магазина, измеряемая в квадратных метрах, а Y — годовой товарооборот, определяемый в миллионах рублей.
Требуется сделать прогноз, какой товарооборот (Y) будет у магазина, если у него та или иная торговая площадь. Очевидно, что функция Y = f (X) возрастающая, так как гипермаркет продает больше товаров, чем ларек.
Видео:Суть метода наименьших квадратов с примерами. Основы эконометрики в RСкачать

Наборы данных
Метод наименьших квадратов используется для обработки набора данных и прогнозирования будущих значений. Пусть у нас есть массивы данных X = и Y = , при этом значение Y зависит от X. Придадим этим массивам смысл. К примеру, массив X – это мощность паровой машины парохода, а Y — его ходовая скорость в узлах. Это означает, что при мощности энергетической установки в 10 тысяч лошадиных сил, пароход развивает скорость на уровне 18 морских миль в час, и так далее, так как каждое значение игрека соответствует своему иксу.
Эти данные можно представить в виде точек на декартовой плоскости, например как V1(X1, Y1), V2(X2, Y2) и так далее. Если соединить эти точки, то мы получим некую кривую, которую можем описать соответствующим уравнением y = f(x). Данное уравнение должно быть достаточно простым, но при этом максимально близко описывать полученную зависимость.
Получив кривую, мы можем продлить ее в любую сторону и узнать приблизительное значение игреков для любых иксов или наоборот. Например, аппроксимировав данные нашего примера, мы сможем узнать, какая мощность установки требуется для достижения скорости в 15 узлов. Или какую мы получим скорость, установив на борт установку мощностью в 22 тысячи лошадиных сил. Для того чтобы определить эту волшебную y = f(x), нам и необходим метод наименьших квадратов.
Видео:Метод наименьших квадратов, урок 1/2. Линейная функцияСкачать
Графическая иллюстрация метода наименьших квадратов (мнк).
На графиках все прекрасно видно. Красная линия – это найденная прямая y = 0.165x+2.184, синяя линия – это 
Для чего это нужно, к чему все эти аппроксимации?
Я лично использую для решения задач сглаживания данных, задач интерполяции и экстраполяции (в исходном примере могли бы попросить найти занчение наблюдаемой величины y при x=3 или при x=6 по методу МНК). Но подробнее поговорим об этом позже в другом разделе сайта.
Чтобы при найденных а и b функция принимала наименьшее значение, необходимо чтобы в этой точке матрица квадратичной формы дифференциала второго порядка для функции 
Дифференциал второго порядка имеет вид:
То есть
Следовательно, матрица квадратичной формы имеет вид
причем значения элементов не зависят от а и b .
Покажем, что матрица положительно определенная. Для этого нужно, чтобы угловые миноры были положительными.
Угловой минор первого порядка 

Угловой минор второго порядка
Докажем, что 
Проверим справедливость неравенства для любого значения n, например для n=2.
Получили верное неравенство для любых несовпадающих значений 

Предполагаем, что неравенство верное для n.

Докажем, что неравенство верное для n+1.
То есть, нужно доказать, что 

Поехали.
Выражение в фигурных скобках положительно по предположению пункта 2), а остальные слагаемые положительны, так как представляют собой квадраты чисел. Этим доказательство завершено.
Вывод : найденные значения а и b соответствуют наименьшему значению функции 
Видео:Метод наименьших квадратовСкачать

Сглаживание ряда методом наименьших квадратов
Задание.
1. Постройте прогноз численности наличного населения города Б на 2010-2011 гг., используя методы: скользящей средней , экспоненциального сглаживания , наименьших квадратов .
2. Постройте график фактического и расчетных показателей.
3. Рассчитайте ошибки полученных прогнозов при использовании каждого метода.
4. Сравните полученные результаты, сделайте вывод.
Решение.
1. Находим параметры уравнения методом наименьших квадратов. Линейное уравнение тренда имеет вид y = bt + a
Система уравнений МНК:
a0n + a1∑t = ∑y
a0∑t + a1∑t 2 = ∑y•t
| t | y | t 2 | y 2 | t•y |
| 1 | 58.8 | 1 | 3457.44 | 58.8 |
| 2 | 58.7 | 4 | 3445.69 | 117.4 |
| 3 | 59 | 9 | 3481 | 177 |
| 4 | 59 | 16 | 3481 | 236 |
| 5 | 58.8 | 25 | 3457.44 | 294 |
| 6 | 58.3 | 36 | 3398.89 | 349.8 |
| 7 | 57.9 | 49 | 3352.41 | 405.3 |
| 8 | 57.5 | 64 | 3306.25 | 460 |
| 9 | 56.9 | 81 | 3237.61 | 512.1 |
| 45 | 524.9 | 285 | 30617.73 | 2610.4 |
Для наших данных система уравнений имеет вид:
9a0 + 45a1 = 524.9
45a0 + 285a1 = 2610.4
Из первого уравнения выражаем а0 и подставим во второе уравнение
Получаем a0 = -0.24, a1 = 59.5
Уравнение тренда:
y = -0.24 t + 59.5
Эмпирические коэффициенты тренда a и b являются лишь оценками теоретических коэффициентов βi, а само уравнение отражает лишь общую тенденцию в поведении рассматриваемых переменных.
Коэффициент тренда b = -0.24 показывает среднее изменение результативного показателя (в единицах измерения у) с изменением периода времени t на единицу его измерения. В данном примере с увеличением t на 1 единицу, y изменится в среднем на -0.24.
Ошибка аппроксимации.
Оценим качество уравнения тренда с помощью ошибки абсолютной аппроксимации.
Ошибка аппроксимации в пределах 5%-7% свидетельствует о хорошем подборе уравнения тренда к исходным данным.
Поскольку ошибка меньше 7%, то данное уравнение можно использовать в качестве тренда.
Однофакторный дисперсионный анализ.
Средние значения
Дисперсия
Среднеквадратическое отклонение
Коэффициент эластичности.
Коэффициент эластичности представляет собой показатель силы связи фактора t с результатом у, показывающий, на сколько процентов изменится значение у при изменении значения фактора на 1%.
Коэффициент эластичности меньше 1. Следовательно, при изменении t на 1%, Y изменится менее чем на 1%. Другими словами – влияние t на Y не существенно.
Эмпирическое корреляционное отношение.
Эмпирическое корреляционное отношение вычисляется для всех форм связи и служит для измерение тесноты зависимости. Изменяется в пределах [0;1].
где ( y -yt)² = 4.4-1.08 = 3.31
В отличие от линейного коэффициента корреляции он характеризует тесноту нелинейной связи и не характеризует ее направление. Изменяется в пределах [0;1].
Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:
0.1 0.3 0.5 0.7 0.9 Полученная величина свидетельствует о том, что изменение временного периода t существенно влияет на y.
Коэффициент детерминации.
т.е. в 75.39% случаев влияет на изменение данных. Другими словами – точность подбора уравнения тренда – высокая.
| t | y | y(t) | (y-ycp) 2 | (y-y(t)) 2 | (t-tp) 2 | (y-y(t)) : y |
| 1 | 58.8 | 59.26 | 0.23 | 0.21 | 16 | 0.00786 |
| 2 | 58.7 | 59.03 | 0.14 | 0.11 | 9 | 0.00557 |
| 3 | 59 | 58.79 | 0.46 | 0.0431 | 4 | 0.00352 |
| 4 | 59 | 58.56 | 0.46 | 0.2 | 1 | 0.0075 |
| 5 | 58.8 | 58.32 | 0.23 | 0.23 | 0 | 0.00813 |
| 6 | 58.3 | 58.09 | 0.0004 | 0.0452 | 1 | 0.00365 |
| 7 | 57.9 | 57.85 | 0.18 | 0.0022 | 4 | 0.000825 |
| 8 | 57.5 | 57.62 | 0.68 | 0.0137 | 9 | 0.00204 |
| 9 | 56.9 | 57.38 | 2.02 | 0.23 | 16 | 0.00847 |
| 45 | 524.9 | 524.9 | 4.4 | 1.08 | 60 | 0.0476 |
Интервальный прогноз.
Определим среднеквадратическую ошибку прогнозируемого показателя.
m = 1 – количество влияющих факторов в уравнении тренда.
Uy=yn+L±K
где
L – период упреждения; уn+L – точечный прогноз по модели на (n + L)-й момент времени; n – количество наблюдений во временном ряду; Sy – стандартная ошибка прогнозируемого показателя; Tтабл – табличное значение критерия Стьюдента для уровня значимости α и для числа степеней свободы, равного n-2.
По таблице Стьюдента находим Tтабл
Tтабл (n-m-1;α/2) = (7;0.025) = 2.365
Точечный прогноз, t = 10: y(10) = -0.24*10 + 59.5 = 57.15
57.15 – 1.08 = 56.07 ; 57.15 + 1.08 = 58.23
Интервальный прогноз:
t = 10: (56.07;58.23)
Точечный прогноз, t = 11: y(11) = -0.24*11 + 59.5 = 56.91
56.91 – 1.14 = 55.77 ; 56.91 + 1.14 = 58.05
Интервальный прогноз:
t = 11: (55.77;58.05)
2. Сглаживаем ряд методом скользящей средней. Одним из эмпирических методов является метод скользящей средней. Этот метод состоит в замене абсолютных уровней ряда динамики их средними арифметическими значениями за определенные интервалы. Выбираются эти интервалы способом скольжения: постепенно исключаются из интервала первые уровни и включаются последующие.
| t | y | ys | Формула |
| 1 | 58.8 | 58.75 | (58.8 + 58.7)/2 |
| 2 | 58.7 | 58.85 | (58.7 + 59)/2 |
| 3 | 59 | 59 | (59 + 59)/2 |
| 4 | 59 | 58.9 | (59 + 58.8)/2 |
| 5 | 58.8 | 58.55 | (58.8 + 58.3)/2 |
| 6 | 58.3 | 58.1 | (58.3 + 57.9)/2 |
| 7 | 57.9 | 57.7 | (57.9 + 57.5)/2 |
| 8 | 57.5 | 57.2 | (57.5 + 56.9)/2 |
| 9 | 56.9 | – | – |
Стандартная ошибка (погрешность) рассчитывается по формуле:
где i = (t-m-1, t)
3. Построим прогноз численности с использованием экспоненциального сглаживания. Важным методом стохастических прогнозов является метод экспоненциального сглаживания. Этот метод заключается в том, что ряд динамики сглаживается с помощью скользящей средней, в которой веса подчиняются экспоненциальному закону.
Эту среднюю называют экспоненциальной средней и обозначают St.
Она является характеристикой последних значений ряда динамики, которым присваивается наибольший вес.
Экспоненциальная средняя вычисляется по рекуррентной формуле:
St = α*Yt + (1- α)St-1
где St – значение экспоненциальной средней в момент t;
St-1 – значение экспоненциальной средней в момент (t = 1);
Что касается начального параметра S0, то в задачах его берут или равным значению первого уровня ряда у1, или равным средней арифметической нескольких первых членов ряда.
Yt – значение экспоненциального процесса в момент t;
α – вес t-ого значения ряда динамики (или параметр сглаживания).
Последовательное применение формулы дает возможность вычислить экспоненциальную среднюю через значения всех уровней данного ряда динамики.
Наиболее важной характеристикой в этой модели является α, по величине которой практически и осуществляется прогноз. Чем значение этого параметра ближе к 1, тем больше при прогнозе учитывается влияние последних уровней ряда динамики.
Если α близко к 0, то веса, по которым взвешиваются уровни ряда динамики убывают медленно, т.е. при прогнозе учитываются все прошлые уровни ряда.
В специальной литературе отмечается, что обычно на практике значение α находится в пределах от 0,1 до 0,3. Значение 0,5 почти никогда не превышается.
Экспоненциальное сглаживание применимо, прежде всего, при постоянном объеме потребления (α = 0,1 – 0,3). При более высоких значениях (0,3 – 0,5) метод подходит при изменении структуры потребления, например, с учетом сезонных колебаний.
В качестве S0 берем первое значение ряда, S0 = y1 = 58.8
| t | y | St | Формула |
| 1 | 58.8 | 58.8 | (1 – 0.1)*58.8 + 0.1*58.8 |
| 2 | 58.7 | 58.71 | (1 – 0.1)*58.7 + 0.1*58.8 |
| 3 | 59 | 58.97 | (1 – 0.1)*59 + 0.1*58.71 |
| 4 | 59 | 59 | (1 – 0.1)*59 + 0.1*58.97 |
| 5 | 58.8 | 58.82 | (1 – 0.1)*58.8 + 0.1*59 |
| 6 | 58.3 | 58.35 | (1 – 0.1)*58.3 + 0.1*58.82 |
| 7 | 57.9 | 57.95 | (1 – 0.1)*57.9 + 0.1*58.35 |
| 8 | 57.5 | 57.54 | (1 – 0.1)*57.5 + 0.1*57.95 |
| 9 | 56.9 | 56.96 | (1 – 0.1)*56.9 + 0.1*57.54 |
Прогнозирование данных с использованием экспоненциального сглаживания.
Методы прогнозирования под названием “сглаживание” учитывают эффекты выброса функции намного лучше, чем способы, использующие регрессивный анализ.
Базовое уравнение имеет следующий вид:
F(t+1) = F(t)(1 – α) + αY(t)
F(t) – это прогноз, сделанный в момент времени t; F(t+1) отражает прогноз во временной период, следующий непосредственно за моментом времени t
Стандартная ошибка (погрешность) рассчитывается по формуле:
где i = (t – 2, t)
Пример . Методом наименьших квадратов найти функции вида y=ax+b , y=ax²+bx+c , аппроксимирующие экспериментальную функцию y=f(x) . В обоих случаях найти суммы квадратов невязок ∑bi². В декартовой системе координат построить экспериментальные точки и графики найденных функций y=ax+b,y=ax^2+bx+c.
Пример №5
Пример №3 . Функция y=y(x) задана таблицей своих значений:
x: -2 -1 0 1 2
y: -0,8 -1,6 -1,3 0,4 3,2
Применяя метод наименьших квадратов, приблизить функцию многочленами 1-ой и 2-ой степеней. Для каждого приближения определить величину среднеквадратичной погрешности. Построить точечный график функции и графики многочленов.
Решение. Функция многочлена 2-ой степени имеет вид y = ax 2 + bx + c .
1. Находим параметры уравнения методом наименьших квадратов. Система уравнений МНК:
a0n + a1∑x + a2∑x 2 = ∑y
a0∑x + a1∑x 2 + a2∑x 3 = ∑yx
a0∑x 2 + a1∑x 3 + a2∑x 4 = ∑yx 2
🔍 Видео
Численные методы: Метод наименьших квадратовСкачать

11 1 Метод наименьших квадратов ВведениеСкачать

Метод Наименьших Квадратов (МНК)Скачать

Аппроксимация в ExcelСкачать

Метод наименьших квадратов. ТемаСкачать

Мораль Лекции по методу наименьших квадратовСкачать

Метод наименьших квадратов. Регрессионный анализ.Скачать

Метод наименьших квадратовСкачать

МНК линейный тренд в MS ExcelСкачать

Построение уравнения линейной регрессии методом наименьших квадратов.Скачать

ЦОС Python #1: Метод наименьших квадратовСкачать

Метод наименьших квадратовСкачать