Метод молекулярной динамики решение уравнения (7 видео)

Содержание

Практическая молекулярная динамика. Часть 1
Определения метода молекулярной динамики
Интегрирование уравнений движения
Методы численного интегрирования
Алгоритм Верле
Силовые поля
Термостат, баростат и все-все-все
Молекулярно-динамические траектории
Метод молекулярной динамики решение уравнения
1.3.3.1 Классическая молекулярная динамика
1.3.3.2 Неэмпирическая молекулярная динамика
Моделирование методом молекулярной динамики в пакете Gromacs
Немного слов… или зачем нам все это надо
Установка
Моделирование
Сахар
Вода + сахар
💡 Видео

Видео:Общее уравнение динамики. Задача 1Скачать

Практическая молекулярная динамика. Часть 1

Серия статей, в которых я постараюсь научить людей работать с методом классической молекулярной динамики и программным пакетом GROMACS в частности. Они основаны на моих приватных лекциях студентам, моем собственном опыте и обсуждениях с коллегами. Я постараюсь рассказывать в доступной форме специально для неподготовленных людей, таким образом (я надеюсь), может рассматриваться как обучающее руководство для новичков. Любые вопросы, комментарии и замечания приветствуются.

Часть 1 содержит введение и некоторые основы метода молекулярной динамики.

Все статьи лицензированы под CC BY-SA, что означает, что вы можете свободно распространять, модифицировать, создавать производные произведения с условием, что вы укажите меня автором оригинального произведения и, в том случае, если вы хотите распространять производную работу, она должна быть под той же лицензией.

Видео:Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Определения метода молекулярной динамики

Метод молекулярной динамики — метод, в котором временная эволюция системы взаимодействующих атомов или частиц отслеживается интегрированием их уравнений движения (Wikipedia). На практике это означает примерно следующее

Для описания движения используются положения классической ньютоновской механики
Силы взаимодействия между частицами задаются в форме каких либо классических потенциальных функций.

Давайте рассмотрим эти положения подробнее.

Надеюсь, вы знаете что такое ньютоновская механика, это что то, строящееся на втором законе Ньютона:

идея данного положения заключается в том, что у нас есть некоторая сила, которая задается по потенциалу (ака первая производная от энергии), есть известная масса, на основании которых мы можем рассчитать ускорение. В дальнейшем простым (на самом деле нет) интегрированием можно получить скорости и — в дальнейшем — координаты.

Возможно, для понимания было бы проще использовать уравнение Лагранжа, которое выглядит следующим образом:

(ну или другие варианты, которые будут рассмотрены ниже)

Второе положение по счастливой случайности описывает то, каким образом мы можем получить значение силы, действующий на частицу (атом) в заданный момент времени. В рамках молекулярной механики используется в основном четыре типа взаимодействия:

внутримолекулярные (они же растяжение связи и деформация плоских углов), которые описываются гармоническим потенциалом:

[U = frac(r-r_0)^2]

внутримолекулярные для описания торсионных углов (там есть свои нюансы, но описываются они, к сожалению, уже не гармониками);

межмолекулярные, описываемые кулоновским законом;

межмолекулярные (они же поляризационные, они же ван-дер-ваальсовые).

Таким образом, энергия взаимодействия одной частицы со всей системой описывается следующим уравнением:

где (U_) и (U_) — гармоники, описывающие взаимодействие между соседними частицами (оно же растяжение связей) и через одну частицу (оно же деформация плоских углов) соответственно, (U_) — деформация торсионных углов, (U_) и (U_) — энергии ван-дер-ваальсового и кулоновского взаимодействия соответственно.

Если обобщить, то потенциальная энергия системы описывается некоторой функцией, которую можно однозначно определить имея текущие координаты частицы и координаты других частиц в системе:

Ну а полная энергия системы будет суммой потенциальных и кинетических энергий всех частиц в системе, что-то вроде:

То есть, зная координаты системы в заданный момент времени, можно рассчитать силу и энергию, на основании которых можно некоторым магическим образом рассчитать новые координаты.

Видео:Основное уравнение динамики вращательного движения. 10 класс.Скачать

Интегрирование уравнений движения

По сути, интегрирование уравнений движения есть решение уравнений Ньютона (или Лагранжа, в зависимости от того, в рамках какого формализма мы рассматриваем систему). Поскольку машины глупые, а вычислительные мощности ограничены, то для их решения используются приближенные методы.

Методы численного интегрирования

Для численного (в отличие от аналитического с первообразными функциями, знакомого по школьной программе) интегрирования используется геометрическое определение интегрирования — определенный интеграл от заданной функции есть площадь фигуры под ней.

Для того, чтобы рассчитать площадь фигуры, можно разбить ее на маленькие части, например, прямоугольные трапеции с заданной шириной (Delta x). Площадь такой трапеции можно рассчитать по формуле

тогда площадь всей фигуры, если ее разбить на (N) равных по ширине трапеций, будет равна

В численных методах (и дальше по тексту) (Delta x) мы будем называть шагом интегрирования и будем считать его предельно малой величиной.

Следует понимать, что приведенный здесь метод является, пожалуй, самым простым для понимания, но отнюдь не единственным (и не самым точным). Более подробно вопросы численного интегрирования будут рассмотрены дальше.

Алгоритм Верле

Допустим, у нас задано время (t) и малый шаг интегрирования (Delta t). Тогда в моменты времени (t + Delta t) и (t — Delta t) координаты можно задать как нечто, что раскладывается в ряд Тейлора в окрестности (t) (пренебрегая членами порядка 3 и выше, поскольку мы предполагаем, что шаг интегрирования бесконечно мал):

[x(t + Delta t) = x(t) + dot x (t) Delta t + frac<ddot x(t) ^2>] [x(t — Delta t) = x(t) — dot x (t) Delta t + frac<ddot x(t) ^2>]

Ничто нам не мешает сложить два уравнения друг с другом и получить следующее:

[x(t + Delta t) + x(t — Delta t) = 2x(t) + ddot x(t) ^2]

[x(t + Delta t) = 2x(t) — x(t — Delta t) + ddot x(t) ^2]

Если перевести на человеческий язык. то, зная координаты частицы в момент времени (t) и немного (на (Delta t)) раньше, а также зная ускорение, мы можем рассчитать координаты частицы в будущем на (Delta t).

Ускорение можно рассчитать исходя из силы, используя второй закон Ньютона (которую, в свою очередь, легко рассчитать дифференцированием энергии), координаты частиц мы, вроде бы, знаем. Но есть нюанс. Безусловно, мы знаем координаты частиц в текущий момент времени, но откуда взять координаты частиц из прошлого, если текущий момент времени равен 0?

Для определения координат частиц в предыдущий 0 момент времени используется примерно следующий хак. Допустим, мы проводим моделирование при заданной температуре (T); воспользовавшись аппаратом статистической физики, мы можем описать распределение частиц по скоростям (например, Максвелловское распределение). Таким образом, можно случайным образом задать частице такую скорость, чтобы температура всей системы была равна заданной. Далее, рассчитать ускорение частицы в нулевой момент времени и, в дальнейшем, собственно координаты частиц в момент времени (t — Delta t).

inb4: Следует понимать, что указанный алгоритм имеет свои недостатки. Например, поскольку скорости явно не учитываются при интегрировании уравнений движения, их расчет имеет некоторую погрешность, что приводит к значительно амплитуде изменения скорости одной частицы со временем (и, как следствие, погрешность при определении кинетической энергии). Также, указанный алгоритм довольно упрощен, для уточнения конкретных реализаций следует читать исходный код (если доступен) соответствующих программных пакетов или научные статьи.

Видео:УРАВНЕНИЯ С МОДУЛЕМ | метод интерваловСкачать

Силовые поля

Внимательный (лол) читатель мог обратить внимание, что, даже если рассматривать относительно простые случаи потенциальных энергий — энергии гармонических осцилляторов — они содержат некоторые магические параметры — (k) и (r_0). Если их физический смысл — я надеюсь — не вызывает вопросов — (k) — это что-то похожее на жесткость пружины, а (r_0) — расстояние в точке минимума — то вопрос, откуда их брать, может вызвать некоторые сложности.

Для их определения, обычно решается обратная задача — исходя из известной энергии рассчитываются вторые производные (они же (k)), а (r_0) рассчитывается исходя из минимума потенциальной энергии. В качестве опорных значений для расчетов энергии используются неэмерические методы (в противовес эмпирической классической молекулярной механике), поголовно состоящие из квантово-химических методов.

Совокупность же параметров, рассчитанных в рамках одного метода с усреднением параметров по определенному принципу (равно как и подгон значений под определенные вполне материальные физические величины) в дальнейшем мы будем называть силовым полем. Вопрос выбора того или иного силового поля, а также принципы, которые лежат в основе их определения, мы рассмотрим позже.

Видео:Применение общего уравнения динамикиСкачать

Термостат, баростат и все-все-все

В методах статистической физики используются вполне определенные ансабмли. У них есть хитрые названия, которые я использовать не буду, потому что они не очень понятны. Принцип их образования примерно следующий: берутся определенные физические величины, которые нам известны в заданной конфигурации, а остальные физические величины рассчитываются исходя из определенных.

В рамках данных статей я буду рассматривать только те системы, в которых число частиц постоянно. Некоторые величины, например, энергия, довольно трудно зафиксировать, поэтому они также не используются при моделировании. По факту, как правило, фиксируется две из трех величин: давление, температура и объем:

канонический ансамбль, в котором фиксируется число частиц, объем и температура (он же (NVT) ансамбль);
изотермо-изобарический ансамбль, в котором фиксируется число частиц, температура и давление (он же (NpT) ансамбль).

В качестве первого приближения можно считать, что объем можно хитрым образом выразить через давление и температуру в системе (уравнение Менделеева-Клапейрона). Тогда задача сводится к — так или иначе — заданию определенного давления и температуры. Для поддержания определенной температуры в системе используется алгоритм, который описывает термостат (обмен температуры системы с окружающей средой). Для давления, соответственно, баростат — “обмен” давления с окружающей средой.

Видео:Метод Ньютона (метод касательных) Пример РешенияСкачать

Молекулярно-динамические траектории

Под траекторией мы будем подразумевать зависимость координат частиц от времени. Также, в виду лени, сюда мы будем относить и все производные физические величины, которые мы можем рассчитать напрямую в ходе моделирования — скорости, ускорения, температура, давление, различные энергии и т.д.

Видео:Идеальный газ. Основное уравнение молекулярно-кинетической теории газов. 10 класс.Скачать

Метод молекулярной динамики решение уравнения

Молекулярная динамика (МД) это техника компьютерного моделирования, позволяющая проследить эволюцию системы взаимодействующих атомов во времени с помощью интегрирования уравнений движения. Несомненным преимуществом метода МД является возможность моделирования системы при заданной температуре или при заданных скоростях атомов (ионов) с достаточно высокой скоростью расчета.

Сейчас МД применяется в квантовой химии и физике твердого тела для [95]:

· изучения дефектов в кристаллах, варьирующихся от точечных (вакансии, дефекты внедрения) до линейных (дислокации) и плоских (межфазные, междоменные границы и т. д.). Для расчета подобных структур нужно применять метод суперячеек, требующих использования большого количества атомов в системе [96];

· реконструкции поверхности кристалла, связанной с перестройкой координат множества атомов на поверхности. Ее можно описать с помощью МД, причем можно проследить изменение поверхности в зависимости от температуры [97];

· изучения кластеров, величина которых варьируется от нескольких атомов до нескольких тысяч, С помощью МД в основном проводится процедура численного отжига при оптимизации геометрии [98, 99];

· изучения биологических молекул (белки, ДНК, РНК и др.), обладающих низкой симметрией и содержащих огромное количество атомов [100].

1.3.3.1 Классическая молекулярная динамика

В классической молекулярной динамике используются законы механики Ньютона. Сила, действующая на атом I , записывается, соответственно, в виде

где M_I масса атома I , его ускорение. В расчетах классической МД используются эмпирические потенциалы (см. выше).

Уравнения движения

Рассмотрим системы N частиц, двигающихся под влиянием потенциальной функции U [101]. Движения частиц можно описать с помощью их координат и импульсов . Обозначим и как и соответственно. Потенциальная функция U зависит только от координат частиц: .

Гамильтониан такой системы имеет следующий вид:

Силу, действующую на частицу, можно вычислить как пространственную производную потенциала:

Таким образом, уравнения движения такой системы можно записать в следующем виде:

Из этих уравнений легко получить второй закон Ньютона:

Уравнения движения также можно получить, используя формализм Лагранжа:

Последнее выражение применяется для получения ab initio МД-уравнений.

Интегрирования уравнений движения, алгоритм Верле

Для того чтобы проследить эволюцию системы, необходимо провести интегрирование уравнений движения, т. е. на основе начальных данных (скоростей и координат частиц) получить их траектории в любой необходимый последующий момент времени. Существует достаточно много различных методов интегрирования уравнений движения. Все они основаны на методе конечных разностей, где время изменяется дискретно с некоторым шагом Δ t .

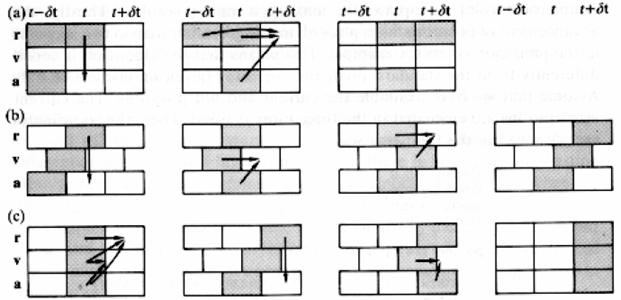
Среди наиболее известных методов интегрирования уравнений движения можно выделить алгоритм Верле [102], алгоритм «прыжков лягушки» ( leap frog ) [103], метод предиктора-корректора [104] (рис. 1-14). В данной книге будет описан первый из этих алгоритмов.

Алгоритм Верле в литературе по численному анализу часто называется неявной симметричной разностной схемой.

Основная идея алгоритма Верле состоит в записи разложения положения частицы и :

Складывая (1.200) и (1.201), можно получить

где ускорение частицы ( ), которое, однако, можно вывести также из выражения

Выражение (1.202) это основное уравнения алгоритма Верле. Данный алгоритм легко использовать, он достаточно точен и стабилен, что объясняет его большую популярность в МД-расчетах. Некоторым его недостатком является то, что он не самостартующий и необходимо использовать другой алгоритм для получения нескольких первых точек координат.

Кроме вышеописанной версии алгоритма Верле, разработан скоростной алгоритм Верле, где положения, скорости и ускорения на шаге t + Δ t вычисляются следующим образом:

Преимуществом скоростной формы алгоритма Верле является то, что она является самостартующей.

Рис. 1-14. Схематическое описание различных форм алгоритма Верле: а основной алгоритм Верле (1.202); b алгоритм «прыжков лягушки»; c скоростная форма алгоритма Верле (1.204) [105].

1.3.3.2 Неэмпирическая молекулярная динамика

Метод неэмпирической молекулярной динамики, впервые предложенный в работе Кара Паринелло ( Car Parinello ) [106], имеет широкое применение в современной физике и химии. В нем потенциальная энергия системы, необходимая для нахождения сил, действующих на атомы, выбирается не параметрически, а рассчитывается квантово-химическим способом для любой конфигурации системы в ходе компьютерного моделирования. В подходе неэмпирической молекулярной динамики электронная система описывается набором волновых функций , которые принадлежат (или лежат очень близко к) основному состоянию для потенциальной поверхности Борна Оппенгеймера в любой момент времени, что позволяет отразить совместное движение электронов и ядер, описываемых набором координат . При этом поведение системы строится исходя из лагранжиана системы, где вводятся фиктивное время и фиктивная масса электронов μ. В предположении, что величина μ >> m_e , фиктивная кинетическая энергия электронов будет оставаться малой по сравнению с кинетической энергией ионов, что позволяет рассчитывать силы, действующие на ядра в любой момент времени, по теореме Гельмана Фейнмана для электронных систем, соответствующих мгновенным ядерным конфигурациям (адиабатическое приближение). Уравнения движения полной динамической системы, включающей фиктивную электронную динамику и действительную ионную динамику, определяются лагранжианом

Видео:Метод молекулярной динамикиСкачать

Моделирование методом молекулярной динамики в пакете Gromacs

Иногда хочется занять свой ноутбук чем-нибудь полезным, да и так чтобы с работой помогало. Несколько лет назад, в университете сталкивался бегло с моделирование методом молекулярной динамики в gromacs, это хоть и не совсем то, но уже можно было притянуть за уши к моей работе. Русскоязычной информации по запуску моделирования в gromacs удалось найти крайне мало, примерно столько же и в глобальном масштабе, все в основном обсуждают уж очень глубокие/тонкие моменты. В итоге решил разобраться в нем, а заодно и написать краткое руководство, по использованию gromacs.

Преследуемая цель статьи — популяризировать Gromacs в широких кругах. Цели сделать полный охват метода и возможностей пакета нету, потому это будет краткий экскурс ~~плохая методичка~~, с установками и запуском.

Немного слов… или зачем нам все это надо

Если говорить о моделировании атомных или молекулярных структур, то практически все методы можно разделить на две группы: Квантово-механические методы и методы молекулярной динамики. Отличие этих групп принципиальное.

Квантово-механические методы основываются на использовании квантовой механики. Используемые в них расчеты ведутся либо из “честных/точных” квантовых уравнений, либо из их некоторых приближений, которые делаются для ускорения расчетов. Стоит отметить, что данные методы могут считать химические реакции т.е. превращения одних веществ в другие с достаточно высокой точностью. Под точностью следует понимать значения энергий связей в системе, разницы до и после реакции. Для лучшего представления точности метода знаю, что бывали ситуации когда посчитанное значение оказывалось точнее измеренного экспериментального. Т.е. более точные эксперименты в будущем подтверждали квантово-механические расчеты. Но данные методы имеют существенный недостаток это требование к большой вычислительной мощности(на “не супер компьютерах” системы в тысячу атомов имеют не приличные времена расчетов). Какие-то цифры по системам я привести не могу, подзабыл.

Молекулярная-динамика основывается на классической ньютоновской механике. Т.е. все взаимодействия считаются классическим образом из “простых” уравнений. В этом и слабость и сила метода. С одной стороны это дает возможности моделировать системы с миллионами атомов. С другой стороны расчеты идут только на уровне межмолекулярного взаимодействия и расчет хим реакций «не возможны», в отличии от квантовой химии, где считается «всё».

Примеры использования gromacs:

Начнем с установки, т.к. она в принципе может вызвать трудности

Установка

Установка gromacs
Можно поставить какую-то сборку из репозитория:

но для хорошей производительности рекомендую произвести сборку самостоятельно, под свое железо(у меня это i5-3210M, geforce 620m):

Скачиваем последнюю, стабильную версию программы, в моем случае это gromacs 5.0.4. Распаковываем и создаем папку для сборки:

далее самый важный момент, из-за которого весь этот неприглядный процесс и затеян — выбор используемых комманд процессора, методов расчета, использования видеокарты итп. Подробнее о используемых методах указано в документации к установке. По порядку, используем для настройки cmake:

использование FFTW: -DGMX_BUILD_OWN_FFTW=ON -DGMX_FFT_LIBRARY=FFTW
выбираем набор процессорных команд, для моего процессора это avx и соответствующая запись -GMX_SIMD=AVX_256 (другие)
поддержка видеокарты -DGMX_GPU=ON -DCUDA_TOOLKIT_ROOT_DIR=/usr/lib/nvidia-cuda-toolkit/ путь до cuda toolkit
-DCMAKE_INSTALL_PREFIX=/usr/local/ выбираем папку установки. Если посмотреть на значения по-умолчанию, то можно увидеть, что установка произведется в /usr/local/gromacs/, что потребует дополнительного прописывания путей, для запуска, потому просто отправляем его в /usr/local.

Настраиваем, собираем и устанавливаем:

Если на каком-то шаге начинает ругаться об отсутствующих пакетах — ставим их. У меня ни на что не срыгнулась, хотя ставил на свежую ubuntu 14.04, так что все должно пройти «гладко».

Подробнее о установке можно найти ~~или не найти~~ в документации.

Установка VMD
VMD это программа визуализации молекул, т.е. просмотра результатов моделирования. Итак регистрируемся на сайте и скачиваем нужную нам версию VMD, рекомендую с поддержкой GPU.

Распаковываем, меняем если нужно пути установки и ставим, не забывая поменять название пакета на vmd и указать версию, при использовании checkinstall

Будем считать что этого нам достаточно и приступим к моделированию.

Моделирование

Моделирование можно разбить на несколько этапов.

Решить что будет моделироваться и с какой целью, отсюда будут отталкиваться параметры моделирования.
Найти/сделать файл с координатами молекул/ы (gro pdb)
Создание топологии молекулы — т.е. сделать описание связей итп. Фактически сказать пакету gromacs с чем он будет работать
Запуск моделирования
- релаксация
- само моделирование
Анализ

Точно по пунктам порбегаться в статье не буду, т.к допустим отличия релаксации и самого моделирования только в конфигурационном файле, а анализ дело специфическое и длинное…

Для наглядности попробуем смоделировать очень простую систему — воду. Координатный файл и файл топологии молекулы воды есть в силовых полях, которые вшиты в сам пакет. Т.к. моделирование чего-либо в воде производится достаточно часто, то существует несколько типов моделей воды и одна из лучших это tip4p-ew. Эту модель воды мы и будем использовать.
В папке громакса, уже есть отрелаксированная модель в 216 молекул воды, её и будем использовать.

Была скопирована отрелаксированная вода, в 216 молекул, далее она была размножена в трех направлениях «на еще одну», получился итоговый файл в 1728 молекул воды. Метод genconf является методом громакса, его описание можно найти в документации.

Наглядно посмотрим за тем, что было сделано:

открывшаяся картинка, не очень не очень красива, сделаем по лучше, для этого откроем graphics->representation и выберем в «drawing method»: VDW

теперь посмотрим, на большую картину «большой» файл воды, отжав D в отображении прошлого и используя file->new molecule, и так же меняем тип отрисовки атомов:

Теперь её отрелаксируем(т.к. 8 блоков на стыках скорее всего не отрелаксированны): для этого потребуются файлы параметра моделирования и топология молекулы, т.е. файлы отражающие то, какие связи в молекуле существуют, какие силы и на что могут действовать итп. Использовать будем поле сил OPLS/AA.

Для избегания возникновения граничных эффектов используется периодические боксы, т.е. на граниах система сталкивается сама с собой. Т.к. моделирование производится в какой-то среде, у которой есть температура, давление, то существуют методы привода к указанным параметрам. Это так называемые баростаты и термостаты, они бывают разных видов и используются на разных этапах моделирования.

Кулоновские сил распространяются на бесконечность, но при этом быстро спадают, потом используется так называемый радиус обрезания или верлет(подробнее в документации).

Для расчетов существует несколько разных алгоритмов, которые отличаются скоростью, и параметрами работы. Допустим некоторые алгоритмы не могут работать не сильно «дестабилизированных» системах, но при этом очень быстрые, когда система в некотором смысле стабильна. Другие же алгоритмы невероятно медлительны, но могут вывести систему из сильного отклонения в слабое итп.

Поля сил — это набор эмпирических параметров описывающих внутри и межмолекулярные взаимодействия, по сути это числа в лернард-джонсовское взимодействие(или морзе или. ), а так же параметры связи в молекуле. Т.е. сила стягивания связи, её длина, сила удержания плоских и двугранных углов итп. Все эти вещи достаточно подробно описаны в документации, а так же легко найти их описания на русском.

Разработчики рекомендуют, если не известно что нужно — использовать поле opls/aa.

Cоздаем файл описывающий топологию используемой системы:

Подробнее о параметрах моделирования можно почитать в документации. Количество используемых параметров может быть намного больше или меньше, зависит от требования условий. Используемые параметры, я нечестно скопировал из примеров когда-то изучаемых мной курсов и для образовательных целей этого вполне хватит.

Документация к gromacs достаточно подробная и если кто-то решит этим плотно заниматься, документацию стоит досконально прочитать, чтобы понимать в каком случае какие методы использовать, допустим того же учета кулоновского взаимодействия.

Запускаем релаксацию, из папки equi:

Чтобы просмотреть, что получилось необходимо произвести «перенос» атомов, которые ушли по граничным условиям в координатном файле моделирования, используя встроенную утилиту громакса trjconv. После чего открываем начальный файл координат vmd и подгружаем в него координаты:

В vmd нажимаем правой кнопкой на h2o_1728.gro, выбираем load data into molecule и там уже выбираем файл trajout.xtc и жмем load. Если кому-то интересно что будет без trjconv, то может подгрузить исходный traj_comp.xtc.

Теперь используя прокрутку в vmd можно наблюдать за движением молекул в процессе моделирования.

По идеи для получения более-менее реальной модели необходимо произвести дальнейшее моделирование, поменяв термостат и баростат и увеличив время самого моделирования примерно в 5-10 раз. Но на воду саму по себе смотреть не очень интересно, куда интереснее будет поместит туда какое-то вещество, допустим сахар. Эта задача оказывается не только интереснее в плане наблюдения, но и в реализации, потому как топологию сахара придется создавать самим, а не брать готовую.

Сахар

Сахаров на самом деле всяких много, т.к. взять конкретный сахар цели нету, то берем первый понравившийся. Да и я особо уже не помню, чем они там по формулам различаются, фруктозы, сахарозы… Я нагуглил вот такой. Беру первый, как я понял это сахароза, посмотрим на него, уже стандартно в vmd, вот только отображение поставим CPK:

Теперь надо получить топологию данной молекулы, т.е. описать кто с кем связан и какие атомы соответствуют атомам в поле сил. Это можно сделать по-разному, регулярный способ мне не известен. Попробуем получить топологию из имеющихся уже данных — связи атомов в файле pdb и информации в поле силы для атомов.

В «хорошем» pdb файле уже описаны связи атомов, потому есть надежда что из него можно сконвертировать топлогию. И эта задача уже решена ранее, если порыться на сайте gromacs, то можно найти скрипты от участников, там и находится данная перловая утилита — topolgen-1.1.
используя её генерируем файл топологии:

если посмотреть на файл топологии то можно увидеть, что на позиции type стоят просто числа, а должны быть названия типов атомов из того набора сил, который используется. Для того чтобы соотнести данную молекулу с полем сил, надо посмотреть какие типы атомов используются, сколько у них связей и что им соответствует в наборе OPLS/AA.

Для этого откроем в vmd снова молекулу, перейдем в representation, сверху нажмем «Create Rep» и сменим отображение на CPK, затем выберем вкладку selections. В Selected atoms удалим все имеющееся и введем serial 1, нажмем apply. Если посмотреть на отображение, то теперь один атом стал круглым, это и есть атом 1. Теперь мы можем соотнести атом с теми что имеются в наборе поля сил. Чтобы это сделать открываем файл поля сил atomtypes.atp, находящийся в /usr/local/share/gromacs/top/oplsaa.ff. И смотрим что подходит для атома углерода связанного с углеродом, кислородом и водородом, т.е. углерод в оксане. Такого там нету, потому будем просто искать подходящий по связям т.е. opls_193, далее меняем в vmd в selected atoms на 2 и ищем для второго атома, я выбрал opls_182 и так далее получаем в итоге файл топологии.

Так же включил поле сил, добавил название молекулы и сделал название основания.
приведена только измененная часть:

Конвертируем координатный файл из pdb в gro, заодно помещая его в коробку 4 на 4 на 4:

Приводим его в соответствие с топологией, подписывая атомы и ставя название основания:

Теперь пробуем запустить моделирование, для упрощения и проверки возьмем тот же файл grompp.mdp, что и использовали для воды.

В ответ получаем сообщения об ошибках. Они нам говорят о том, что в поле сил нету внутримолекулярного взаимодействия для углов, при заданных типах атомов(файл ffbonded.itp). Это вполне разумно, потому как сбор молекулы производился вручную, из не соответствующих атомов(надо было оксан, а его нету), а какие больше подошли. Возможно некими хитрыми комбинациями и можно запустить моделирование, так чтобы атомы были «нужные», но это уже будет скорее всего неверно. Так же будет неточность в моделировании по причине отсутствия эффективного заряда на атомах, — это столбец charge в файле топологии. Естественный вопрос возникает, откуда брать все эти числа? Можно как-то из экспериментов, а можно и посчитать. Заряды бывает считают теоретически, на бумаге (малликен), но это не сильно точно, куда лучше методом квантовой химии, только считать одну молекулу а не группу. Квантовая химия позволяет найти и внутри молекулярное взаимодействие.

Квантомеханические расчеты производятся в различных программах~~гауссиан~~, и их описание заслуживает отдельных статей и вообще их использование трудозатратно. Но выходом из положения является некоторый сервис — ATB. Он позволяет удаленно на облаке рассчитывать не большие молекулы, а так же индексирует уже посчитанные, что позволяет найти необходимую топологию, сразу без расчетов. Однако используемое в нем поле сил gromos54a7, а значит соответствия атомов с полем сил opls/aa не будет(колонка type в top файлах). Выходом из ситуации может быть, как использования того же поля что и в ATB, так и модификация уже созданной нами топологии для задания внутримолекулярного взаимодействия, на основании расчетов в ATB, однако это требует экспериментальной проверки, т.к. «комбинация» из двух полей не лучший вариант.

После не долгих поисков в репозитории ATB нашел сахарозу. Создадим папку ATB, куда и скачаем файлы топологии и расположения атомов(берем all-atoms). Получается ранее проделанные действия с сахаром были бесполезны, но целью их было показать построение топологии.
В итоге получили 2 файла sug.top и sug.pdb. Запустим моделирование на их основе и файла параметров моделирования, который использовали для воды – в файл топологии дописываем:

добавлено в начало

Поместим 4 молекулы в одну «коробку»:

Возьмем файл параметров моделирования воды, увеличим время в 10 раз и запустим:

Результаты можно посмотреть в vmd.

Вода + сахар

Вода для данного силового поля рекомендованная spc, она хуже чем tip4p, но не будем усложнять и так перегруженную статью, используем spc.

Совместим воду и сахар:

Создаем файл топологии для смешанной системы:

Далее запускаем моделирование:

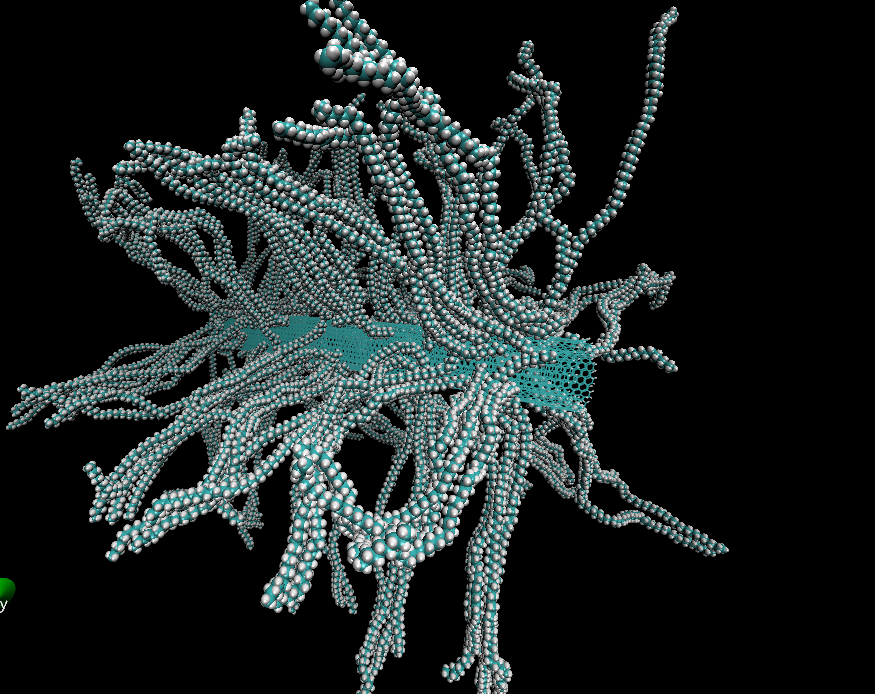
Скорее всего получим ошибку, вызванную тем, что система сильно далеко от равновесия. Для решения данной проблемы — уменьшим шаг моделирования в 2 раза, до 0,001ps (в файле grompp.mdp строчка dt = 0.002; 2 fs). Для наглядности, я промоделировал до времени в 300ps. Результат приведен ниже.

Для дальнейшего анализа можно использовать методы встроенные в gromacs такие как функции радиального распределения, энергии, температуры итп, подробнее можно найти в документации. На анализе я останавливаться не буду ибо статья и так уже по моим меркам большая.