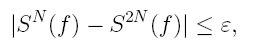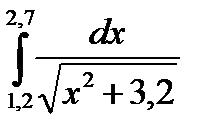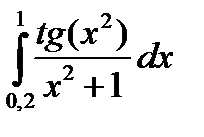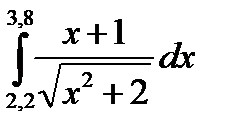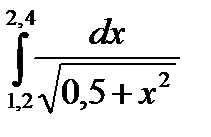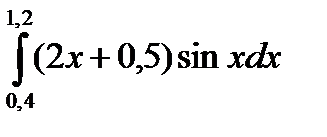Цель — ознакомить студентов с методом Милна четвертого порядка решения задачи Коши для обыкновенных дифференциальных уравнений.
Рассмотрим еще один широко известный метод прогноза и коррекции — метод Милна.
Для вывода первой формулы Милна (т.е. формулы предсказания) проинтегрируем данное уравнение (1) на промежутке [xi-3, xi+1] и в полученном интегральном равенстве
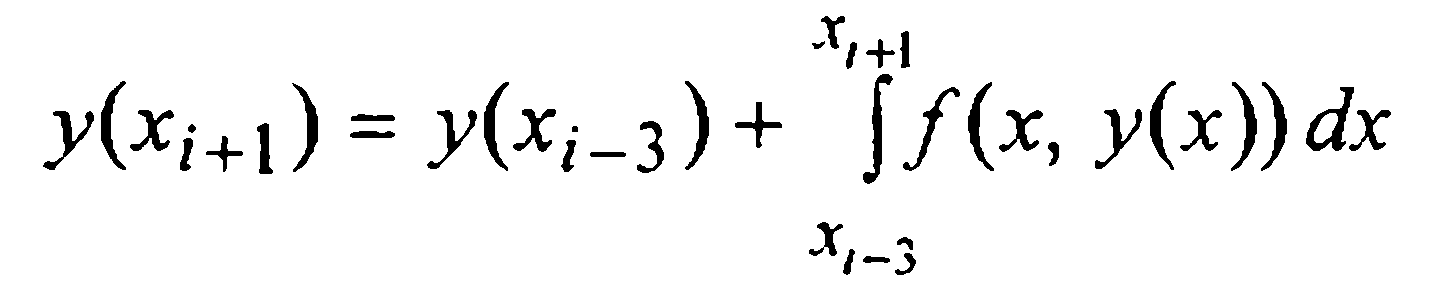
подынтегральную функцию f(x,у(х)) заменим первым интерполяционным многочленом Ньютона Р3(х), построенным по четырем узлам 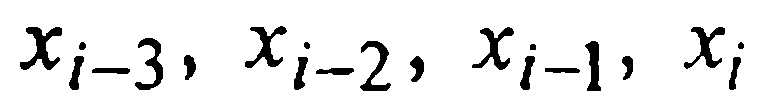
Тогда, после замены переменной 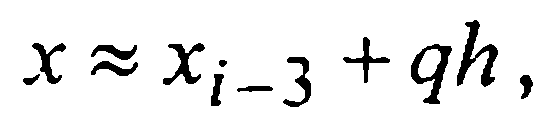
Отсюда, выразив конечные разности через значения функции, получаем первую формулу Милна (предсказания)
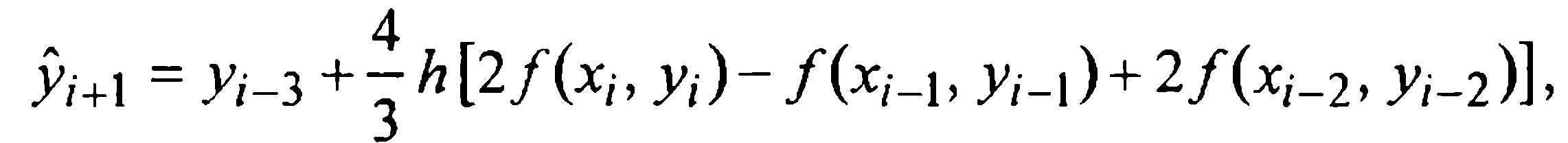
которую, очевидно, следует отнести к экстраполяционным.
Главный член локальной погрешности формулы (27) находим интегрированием следующего (первого из неучтенных) слагаемого интерполяционного многочлена Ньютона. Именно:
Считая четвертые разности примерно одинаковыми, опустим индекс у функции f в записи 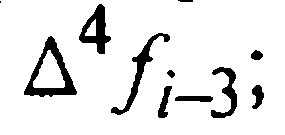
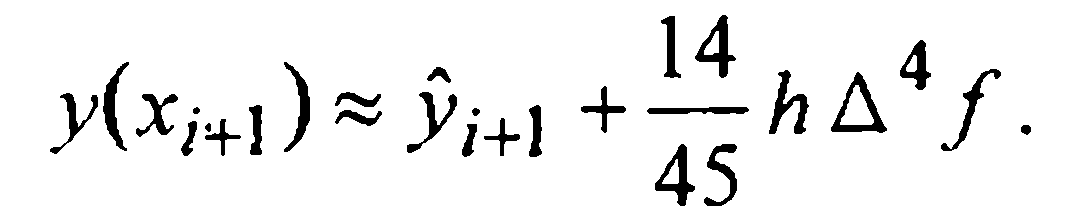
Вывод второй формулы Милна более прост. Проинтегрируем уравнение (1) теперь на промежутке [xi-1, xi+1] и в полученном равенстве
применим к интегралу простейшую формулу Симпсона. Имеем
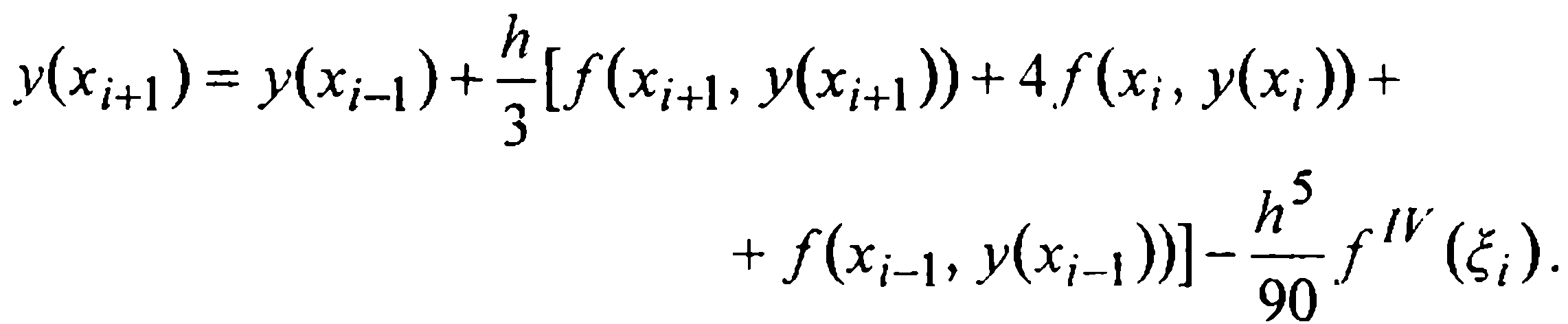
Отбрасывая здесь остаточный член и заменяя значения решения y(xi-1) и y(xi😉 известными приближенными значениями yi-1 и yi, а стоящее в правой части под знаком функции f неизвестное значение у(хi+1) тем значением 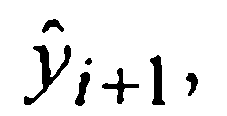
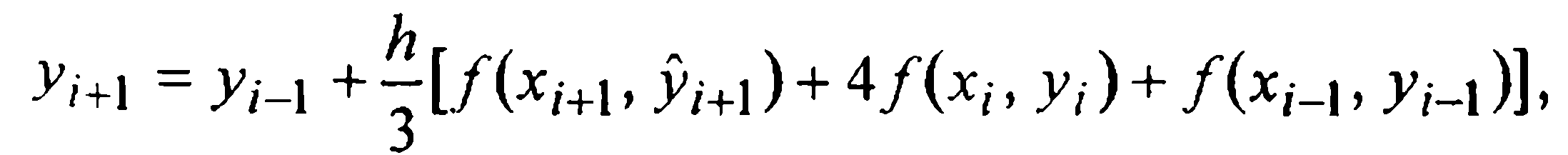
Для вывода приближенной оценки шаговой погрешности воспользуемся приближенным равенством 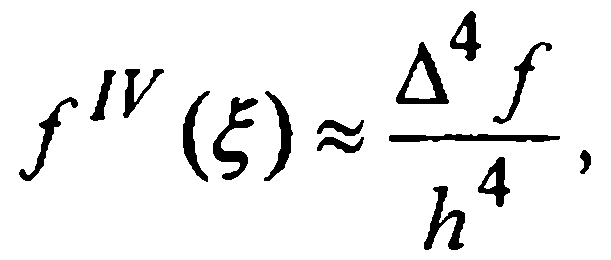
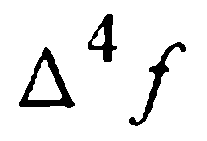

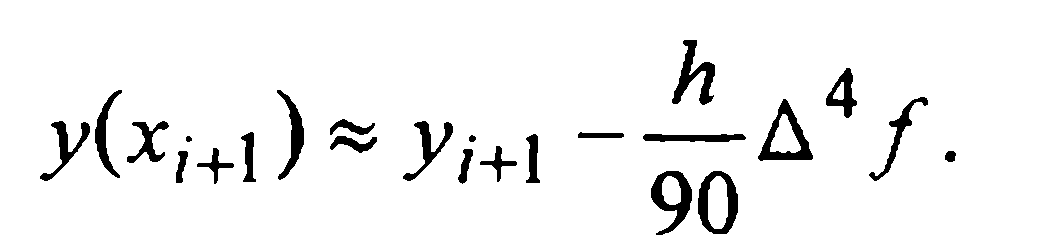
Сравнение (28) и (31) дает:
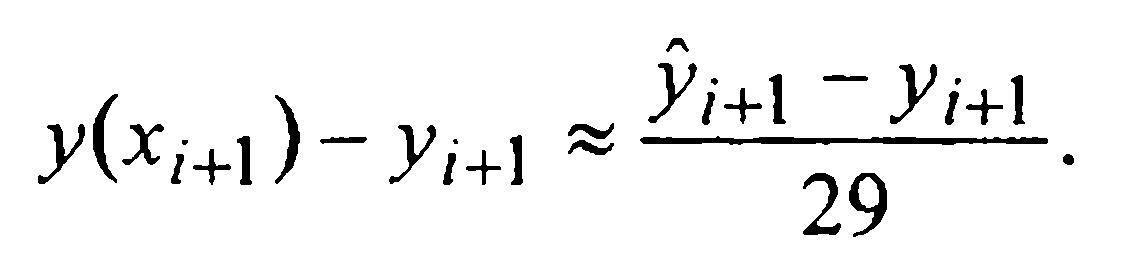
Таким образом, при численном интегрировании начальной задачи (1)-(2) методом Милна четвертого порядка, определенным формулами (27) и (30), на каждом i-м шаге следует вычислять величину
и сравнивать ее модуль с величиной ε > 0 допустимой шаговой погрешности. Если 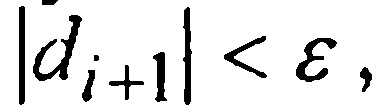
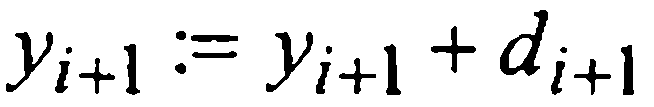
Фигурирующая в приближенном равенстве (32) постоянная 1/29 примерно вдвое меньше постоянной 19/270≈1/14 в аналогичном равенстве (24) для предиктор-корректорного метода Адамса четвертого порядка (22), что характеризует метод Милна как несколько более точный при одинаковых вычислительных затратах.
Приложение 1
Полиномы Лежандра являются специальными функциями, которые применяются при решении многих теоретических и прикладных задач. Полином Лежандра n-й степени можно определить с помощью производной n-го порядка следующим образом:
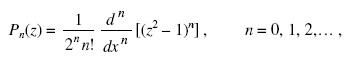
где z — комплексная переменная.
В данном учебном пособии рассматриваются и используются полиномы Лежандра для действительного аргумента x, лежащего в интервале x∈[-1, 1].
Видео:19. Метод вариации произвольных постоянных. Линейные неоднородные диф уравнения 2-го порядкаСкачать

С помощью определения (1) легко получить явные выражения полиномов Лежандра действительного аргумента низших степеней:
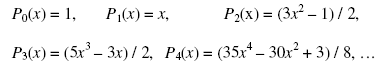
Графики перечисленных полиномов приведены на рис.1.
Все полиномы Лежандра Pn(x) имеют следующие граничные значения:
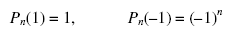
Нетрудно убедиться, что полиномы Лежандра четной степени являются четными функциями и наоборот.
Важным для практических применений является свойство ортогональности полиномов Лежандра:
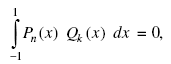
где Qk(x) — любой полином степени k, меньшей n (k
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
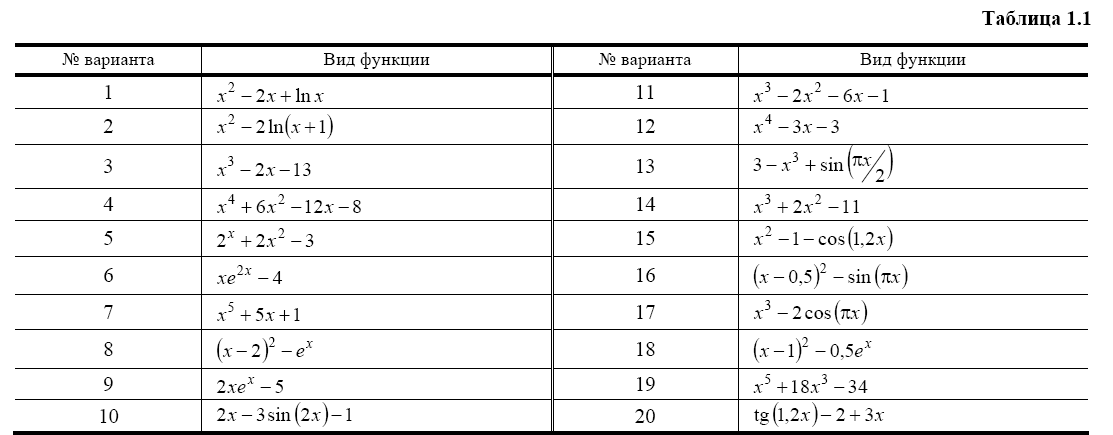
2. Ознакомьтесь с методами приближенного вычисления корней уравнений. Найдите один действительный корень уравнения с точностью 10 -5 . В ходе решения осуществить следующие шаги:
2.1. Отделить корень уравнения.
2.2. Вычислить с помощью программы значение отдельного корня методами: деление отрезка пополам, хорд, касательных, комбинированным методом, методом итераций. При использовании метода простых итераций найти решение при разных начальных приближениях. Результаты вычислений занести в таблицу.
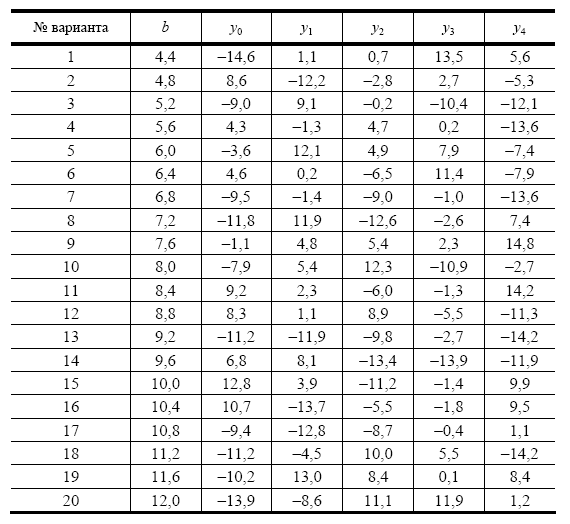
Вариант задания выбрать из табл. 1.1.
3. Найдите действительный корень уравнения с точностью 10 -4 , на интервале [a,b]. На первом этапе решения методом деления пополам, уменьшать интервал, содержащий корень, до тех пор, пока его длина не станет меньше 0,2. Потом, применить один из «более» быстрых методов.
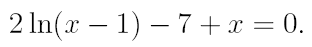 | 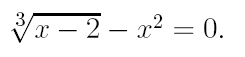 |
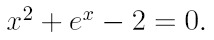 | 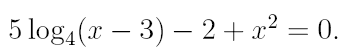 |
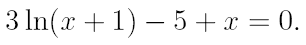 | 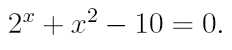 |
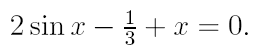 | 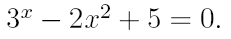 |
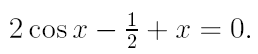 |  |
 | 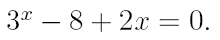 |
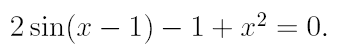 |  |
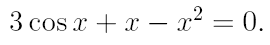 | 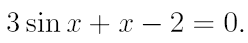 |
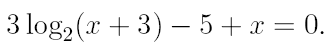 | 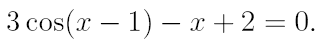 |
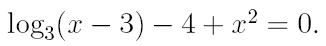 | 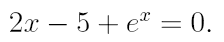 |
Отчет должен содержать:
1. График исследуемой функции с интервалами отделения корней.
2. Таблицы пошаговых расчетов корня уравнения.
3. Обоснованное заключение о преимуществах и недостатках использования исследованных методов решения применительно к заданному уравнению (для задания 1).
4. Используя схему Гаусса (схема единственного деления и схема полного выбора) решить систему уравнений
5. Решить систему уравнений двумя способами — методом итераций и методом Зейделя. Продолжать итерации до тех пор, пока точность приближенного решения не станет меньше 0,01.
Индивидуальное задание №2.
Видео:7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать

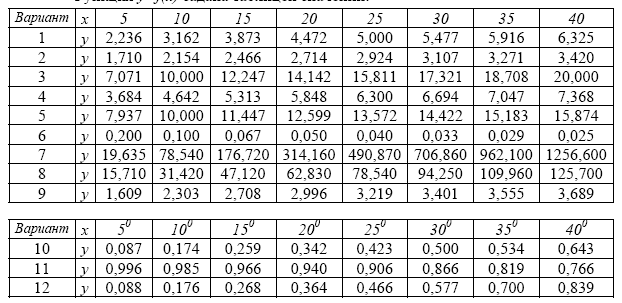
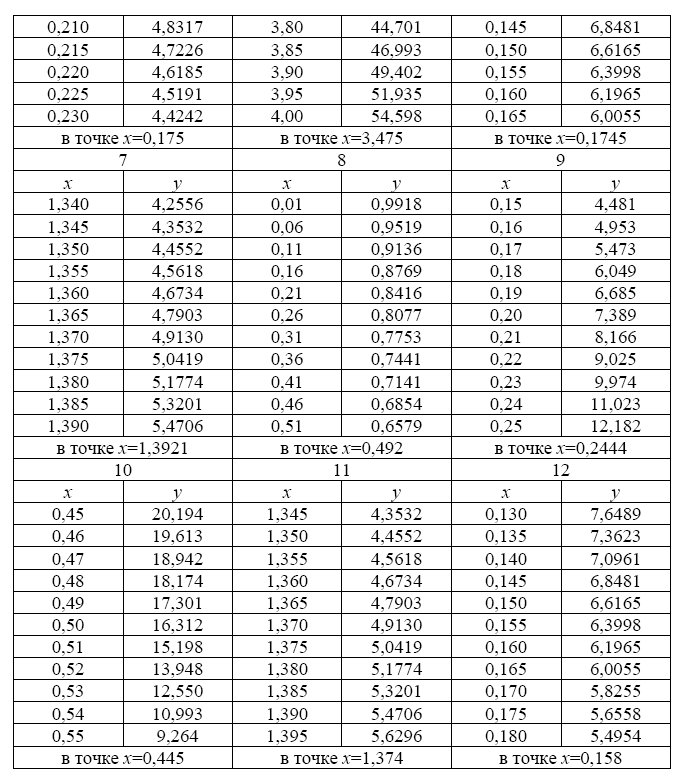
1. Функция y=f(x) задана таблицей значений:
Указания. Для вариантов 10 — 12 значения аргумента x предварительно перевести из градусов в радианы.
Даны контрольные значения аргумента x1=12; x2=26; x3=42.
a) Написать подходящие для приближенного вычисления значений y1=f(x1), y2=f(x2), y3=f(x3) интерполяционные многочлены Лагранжа первой и второй степени. Получить эти значения.
b) Составить алгоритм и написать программу на языке высокого уровня, реализующую схему Эйткена вычисления с максимально возможной точностью значения y=f(x) в произвольной точке x промежутка 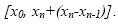
c) Сделать анализ результатов заданий 1, 2.
2. Для заданной таблично функции построить все возможные интерполяционные многочлены Ньютона максимальной степени, пригодные для определения значения функции в указанных промежуточных точках 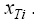
3. Вычислить значения данной функции и ее прозводной с помощью интерполяционного полинома Лагранжа Ln(x). В качестве узлов интерполяции взять:
1) равномерно распределенные точки на отрезке [a; b];
2) чебышевский набор узлов на отрезке [a; b].
При табулировании функции вычислять ряд с точностью 10 -6 .
Замечание. При вычислении ряда 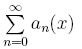
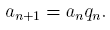
4. Найти приближенные значения функции при данных промежуточных значениях аргумента с помощью кубического сплайна и визуализируйте результаты сплайн-интерполяции.
Отчет должен содержать:
ü постановку задачи и исходные данные;
ü описание методов решения;
ü графики, полученных интерполяционных многочленов;
ü листинг программы.
Индивидуальное задание №3
1. Используя данные таблицы 1, вычислить производную указанной функции в точке х (точка х не является узлом таблицы)
Видео:Метод ЭйлераСкачать

2. Используя данные таблицы 1, вычислить производную указанной функции в точке х (точка х – узел таблицы)
Таблица 1.
| Вариант | Задание 1. | Задание 2. | ||
| Таблица № | х | Таблица № | х | Используемая формула |
| 3.0 | 2 (взять 5 последних значений) | 5,3 | Лагранжа | |
| 3.5 | 3 (взять 4 последних значения) | 6,7 | Лагранжа | |
| 2.5 | 2,6 | Ньютона | ||
| 5.8 | -3,2 | Ньютона | ||
| 3.1 | 2,3 | Ньютона | ||
| 3.9 | 2,1 | Ньютона | ||
| 3.3 | 4 (взять 5 первых значений) | -0,8 | Лагранжа | |
| 6.0 | 5 (взять 4 первых значения) | 3,8 | Лагранжа | |
| 3.2 | 2 (взять 5 первых значений) | 2,9 | Лагранжа | |
| 5.3 | 1,6 | Ньютона | ||
| 3.9 | 3,4 | Ньютона | ||
| 7.2 | 5 (взять 4 первых значения) | Лагранжа | ||
| 4.4 | 6,2 | Ньютона | ||
| 3.6 | 3 (взять 5 последних значений) | 4,5 | Лагранжа | |
| 2.2 | 4 (взять 5 последних значений) | Лагранжа | ||
| 6.8 | 3,7 | Ньютона | ||
| 3.4 | 5,6 | Ньютона | ||
| 3.7 | 4 (взять 4 последних значения) | 6,4 | Лагранжа | |
| 1.8 | 5 (взять 5 первых значений) | 7,4 | Лагранжа | |
| 7.6 | 4,5 | Ньютона |
Таблица 2.
| Таблица 3.
| ||||||||||||||||||||||||||||||||
Таблица 4.
| Таблица 5.
|
3. Вычислить значения интеграла, используя квадратурные формулы:
· Гаусса с двумя узлами.
Интеграл вычислить с точностью ε=10 -6 . Точность вычисления интеграла определяется сравнением результатов при различном числе разбиений отрезка интегрирования. Именно, точность ε считается достигнутой, если
здесь 
Отчет должен содержать:
· постановку задачи и исходные данные,
· описание методов решения и расчетные формулы,
· таблицы значений интегралов с указанием числа разбиений, потребовавшихся для достижения заданной точности,
1. 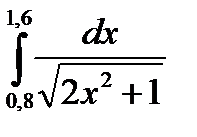

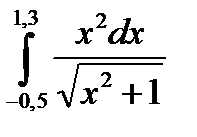
5. 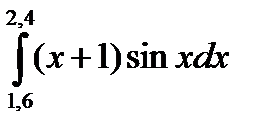
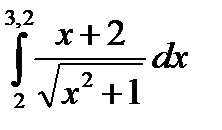

9. 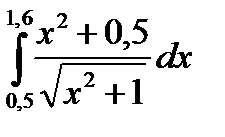
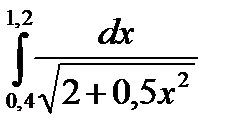
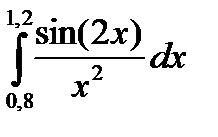
13. 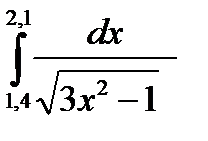
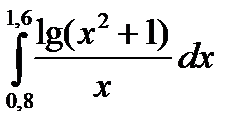

17. 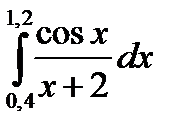
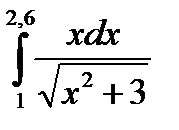

Литература
1. Бахвалов Н. С. Численные методы: учеб. пособие для вузов/ Н. С. Бахвалов, Н. П. Жидков, Г. М. Кобельков. — 4-е изд.; Гриф МО. — Москва: БИНОМ. Лаборатория знаний, 2006. — 636 с. — (Классический университетский учебник). — Библиогр.: с. 624-628. — Предм. указ.: с. 629-632.
2. Вержбицкий В. М. Численные методы: Линейная алгебра и нелинейные уравнения: учеб. пособие для вузов / В. М. Вержбицкий. — 2-е изд., испр.; Гриф МО. — Москва: ОНИКС 21 век, 2005. — 431 с.: ил. — Библиогр.: с. 419-424. — Предм. указ. с. 425-429.
3. Демидович Б. П. Численные методы анализа: приближение функций, дифференциальные и интегральные уравнения: учеб. пособие / Б. П. Демидович, В. А. Марон, Э. З. Шувалова; под ред. Б. П. Демидовича. — Изд. 4-е, стер. — Санкт-Петербург: Лань, 2008. — 400 с. — (Классическая учебная литература по математике). — Библиогр. в конце гл.
4. Киреев В. И. Численные методы в примерах и задачах: учеб. пособие для вузов/ В. И. Киреев, А. В. Пантелеев. — Изд. 2-е, стер.; Гриф УМО. — Москва: Высш. шк., 2006. — 480 с.: ил. — (Прикладная математика для ВТУЗов). — Библиогр.: с. 477-480 .
5. Пантина И. В. Вычислительная математика [Электронный ресурс] учебник для вузов/ И. В. Пантина, А. В. Синчуков. — 2-е изд., перераб. и доп. — Москва: Синергия, 2012. — 175 с.
6. Пирумов У. Г. Численные методы: учеб. пособие для вузов/ У. Г. Пирумов. — 2-е изд., испр. и доп.; гриф МО. — Москва: Дрофа, 2003. — 221 с.: ил. — (Высшее образование). — Библиогр.: с. 216. — Имен. указ.: с. 217.
7. Срочко В. А. Численные методы: курс лекций / В. А. Срочко. — Гриф УМО. — Санкт-Петербург [и др.]: Лань, 2010. — 202 с. — Библиогр.: с. 200.
8. Турчак Л. И. Основы численных методов: учеб. пособие / Л. И. Турчак, П. В. Плотников. — Изд. 2-е, перераб. и доп.; Гриф МО. — Москва: ФИЗМАТЛИТ, 2005. — 300 с.: ил. — Библиогр.: с. 290-292. — Прил.: с. 286-289. — Предм. указ.: с. 293-300.
Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

9. Шевцов Г. С. Численные методы линейной алгебры: учеб. пособие для мат. напр. и спец. / Г. С. Шевцов, О. Г. Крюкова, Б. И. Мызникова. — Гриф УМО. — Москва: Финансы и статистика: ИНФРА-М, 2008. — 479 с. — (Финансы и статистика). — Библиогр.: с. 473-474. — Предм. указ.: с. 475-479.
🔥 Видео
Практика 1 ИзоклиныСкачать

Численное решение задачи Коши методом ЭйлераСкачать

9. Метод вариации произвольной постоянной ( метод Лагранжа ). Линейные дифференциальные уравнения.Скачать

Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Сеточные методы решения дифференциальных уравнений в частных производных.Скачать

Математика без Ху!ни. Линейное неоднородное уравнение 1 порядка. Метод вариации постоянной.Скачать

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Видеоурок "Системы дифференциальных уравнений"Скачать

Дифференциальные уравнения. Задача Коши. Метод Эйлера.Скачать

Метод Лагранжа & Метод Бернулли ★ Решение линейных неоднородных дифференциальных уравненийСкачать

12. Интегрирующий множитель. Уравнения в полных дифференциалахСкачать

Видеоурок "Нахождение частных решений по виду правой части"Скачать

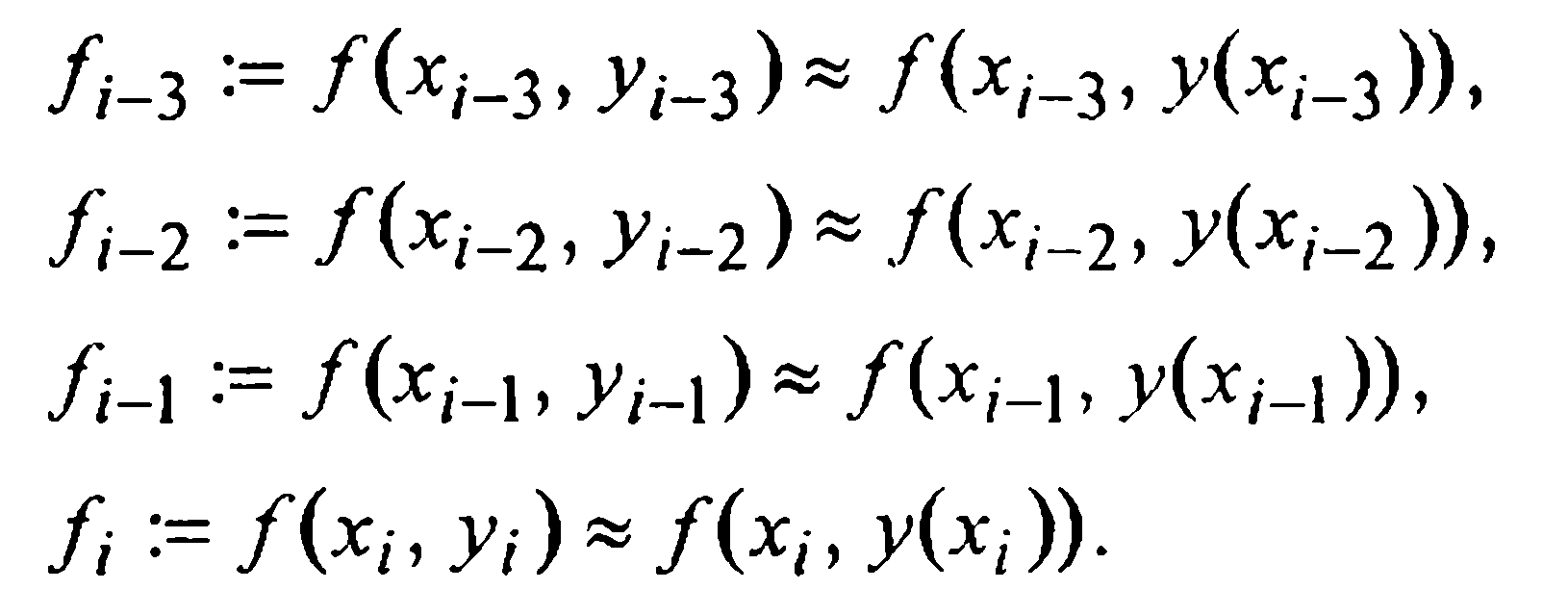
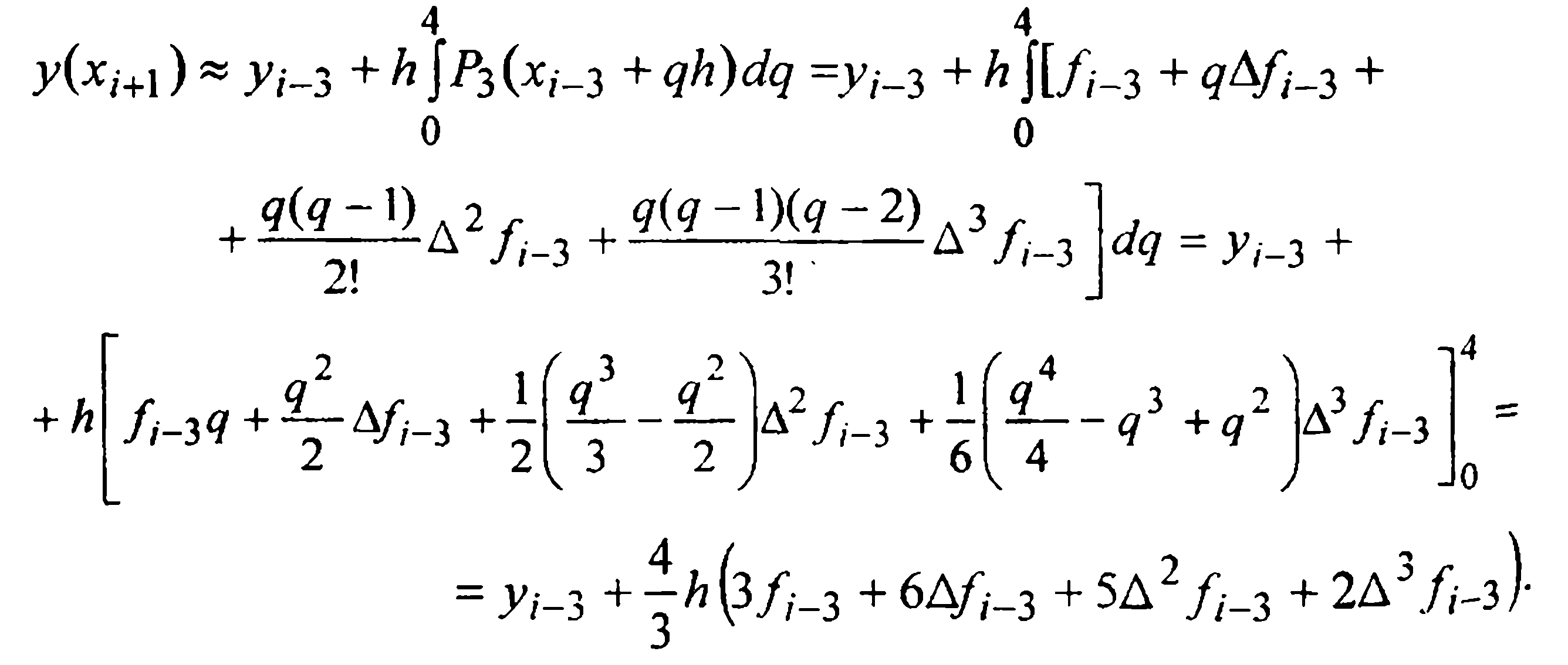
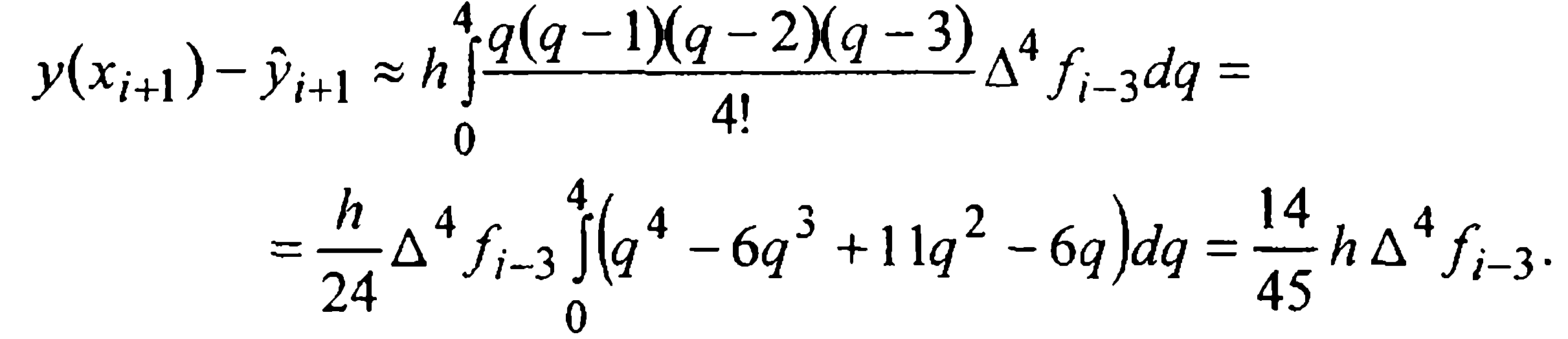
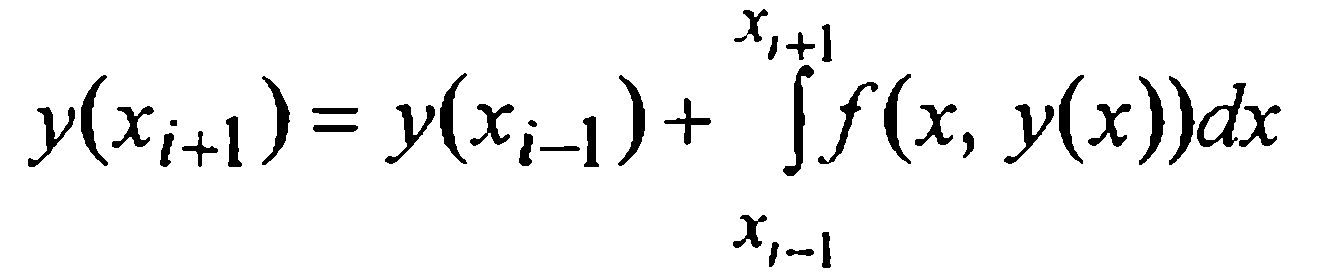
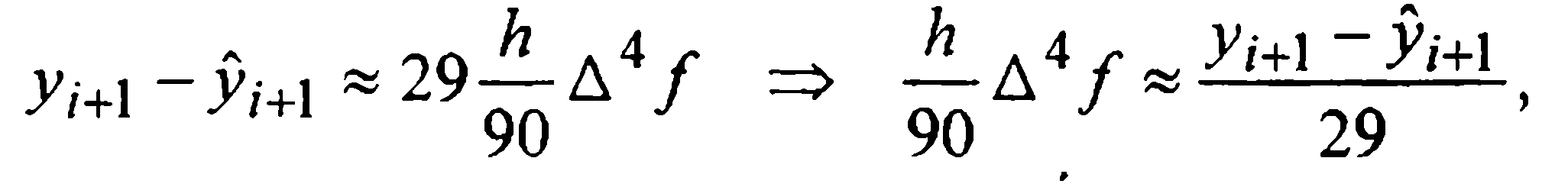
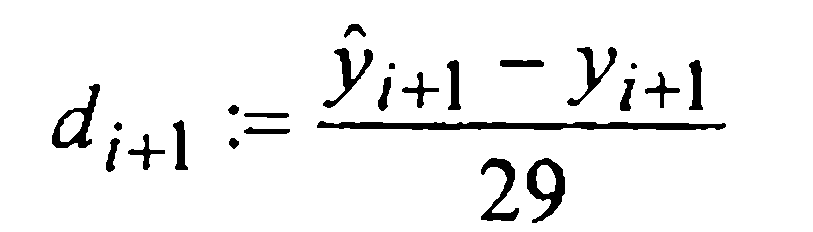

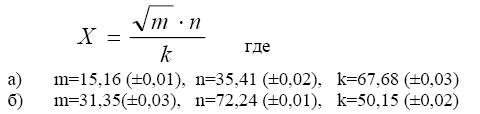
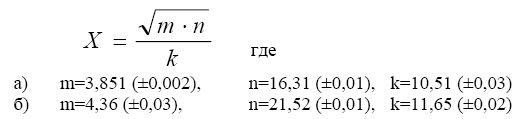
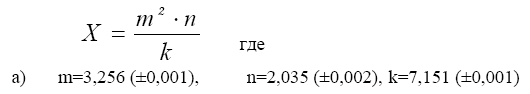



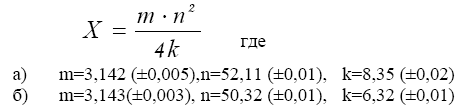
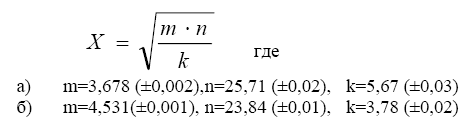

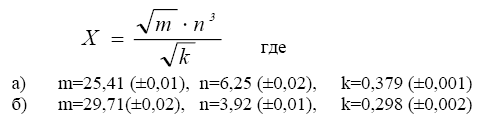
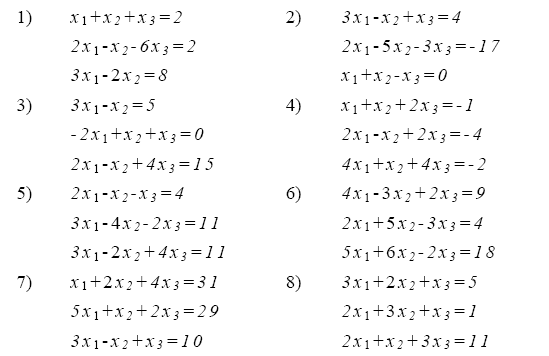
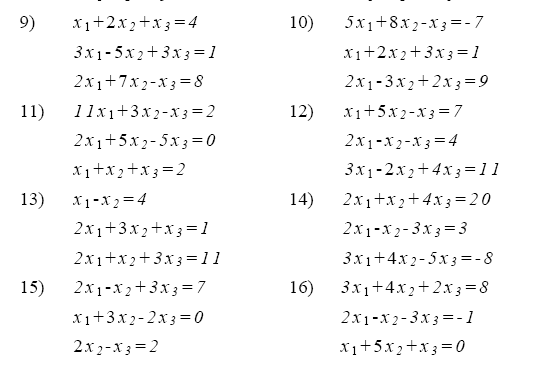
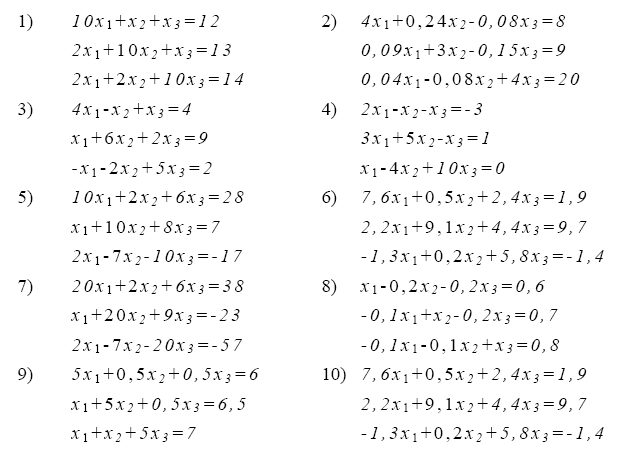


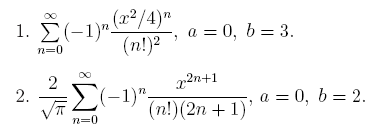
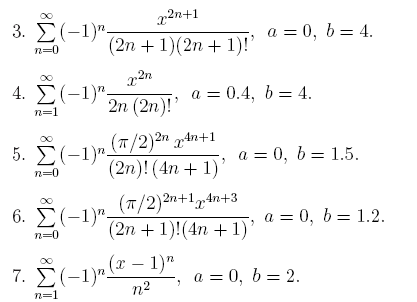
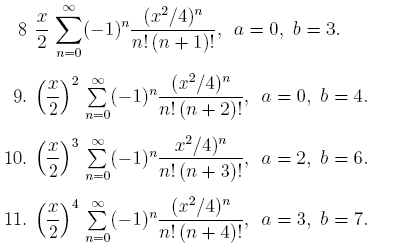

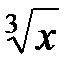 -cos(0,4-0,7x)
-cos(0,4-0,7x)