Метод lu разложения решения систем линейных уравнений (2 видео)

Решение СЛАУ методом LU-разложения

Пусть система уравнений задается в виде:

Пример №1 . Дана система линейных уравнений. Решить ее методом LU-разложения.
Решение. Алгоритм декомпозиции основан на идее представления исходной матрицы в виде произведения двух треугольных матриц. Пусть задана квадратная матрица:
Представим A в виде: A=BC
Покажем пример вычислений нескольких значений матриц B и C.
Вычисляем значение элемента b₁₁=1
c₁₁=1/1=1
c₁₂=3/1=3
c₁₃=3/1=3
Вычисляем значение элемента b₂₁=1
Вычисляем значение элемента b₂₂=-2 — (1 • 3)=-5
c₂₂=-5/(-5)=1
c₂₃=0/(-5)=0
Вычисляем значение элемента b₃₁=3
Вычисляем значение элемента b₃₂=3 — (3 • 3)=-6
Вычисляем значение элемента b₃₃=-1 — (3 • 3 -6 • 0)=-10
c₃₃=-10/(-10)=1

1	0	0
1	-5	0
3	-6	-10

1	3	3
0	1	0
0	0	1

Вычисляем значения y_i
y₁ = 11/1 = 11
y₂ = (1 — 1 • 11 )/(-5) = 2
y₃ = (1 — 3 • 11 -6 • 2 )/(-10) = 2
Вычисляем значения x_i
x₃ = y₃ = 2
x₂ = 2 — (0 • 2 ) = 2
x₁ = 11 — (3 • 2 + 3 • 2 ) = -1

Пример №2 . Решить систему уравнений Ax = b методом Гаусса (LU-разложения).

Содержание

Решение СЛАУ методом LU-разложения
Алгоритм
О песочнице
О модерации
Решение СЛАУ методом LU-разложения
🎬 Видео

Видео:Линал 3.9. LU-разложениеСкачать

Решение СЛАУ методом LU-разложения

LU-разложение — это представление матрицы A в виде A=L•U, где L — нижнетреугольная матрица с еденичной диагональю, а U — верхнетреугольная матрица. LU-разложение является модификациеё метода Гаусса. Основные применения данного алгоритма — решение систем алгебраических уравнений, вычисление определителя, вычисление обратной матрицы и др.

Рассмотрим алгоритм на примере матрицы

Алгоритм

Создаем матрицы

и
Для каждого столбца j = 1… 3 матрицы будем вычислять как

Для каждой строки вычислим

Выполняем шаг 2 пока j

Видео:2_4. LU-разложениеСкачать

О песочнице

Это «Песочница» — раздел, в который попадают дебютные посты пользователей, желающих стать полноправными участниками сообщества.

Если у вас есть приглашение, отправьте его автору понравившейся публикации — тогда её смогут прочитать и обсудить все остальные пользователи Хабра.

Чтобы исключить предвзятость при оценке, все публикации анонимны, псевдонимы показываются случайным образом.

Видео:LU разложение матрицыСкачать

О модерации

Не надо пропускать:

рекламные и PR-публикации
вопросы и просьбы (для них есть Хабр Q&A);
вакансии (используйте Хабр Карьеру)
статьи, ранее опубликованные на других сайтах;
статьи без правильно расставленных знаков препинания, со смайликами, с обилием восклицательных знаков, неоправданным выделением слов и предложений и другим неуместным форматированием текста;
жалобы на компании и предоставляемые услуги;
низкокачественные переводы;
куски программного кода без пояснений;
односложные статьи;
статьи, слабо относящиеся к или не относящиеся к ней вовсе.

Видео:Матричный метод решения систем уравненийСкачать

Решение СЛАУ методом LU-разложения

Метод LU — разложения (декомпозиции) — один из способов решения системы линейных уравнений. Алгоритмы метода схожи с алгоритмами метода Гаусса.

Суть метода состоит в том, чтобы представить исходную матрицу коэффициентов А как произведение двух треугольных матриц.

А = LU, где L — нижняя треугольная матрица с единичной диагональю, U — верхняя треугольная матрица. LU — разложение возможно, когда:
— матрица А обратима;
— главные миноры матрицы отличны от 0.

LU — разложение используют для решения систем линейных уравнений вида: Ах = b.

Т.к. А = LU, исходную систему можно представить в виде равенства: LUх = b. Если ввести вектор у = (у₁, у₂. у_n) t , равенство можно представить как систему: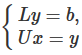
Т.е. решение системы Ах = b заключается в решении двух систем с треугольными матрицами: Lу = b, Uх = у.

На первом этапе решается система Lу = b. Т.к. L — нижняя треугольная матрица, система решается прямой подстановкой.

Запишем первую систему в виде: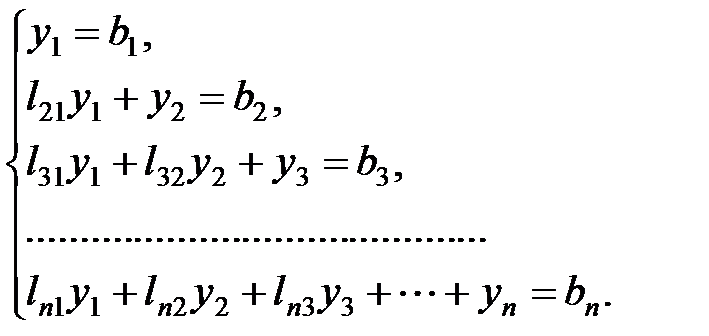
В первом уравнении вычисляем у₁, во втором — у₂, в третьем — у₃ и т.д.

Общая формула: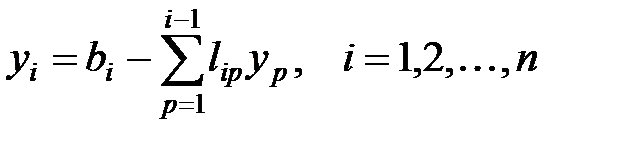
На втором этапе решается вторая система Uх = у способом обратной подстановки.
Система имеет вид: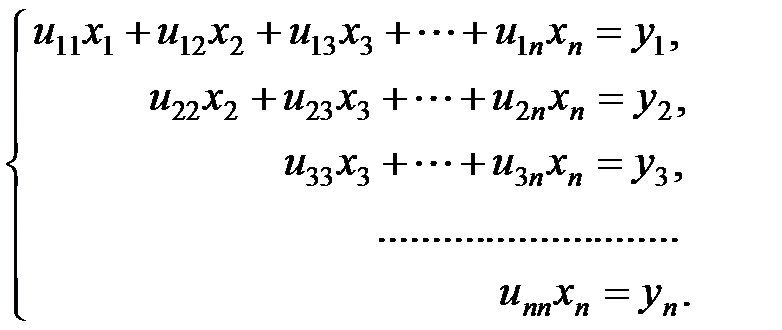
Из последнего уравнения системы находим х_n, из предпоследнего х_n-1 и т.д., из первого находим х₁.
Общая формула для решения системы имеет вид: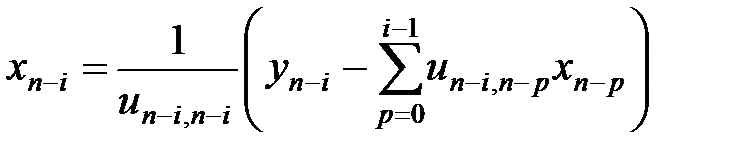
Быстро решать системы линейных уравнений методом LU — разложения можно с помощью онлайн калькулятора.