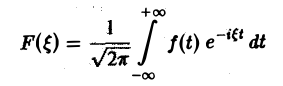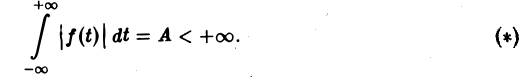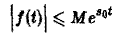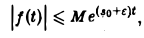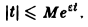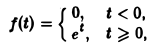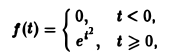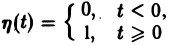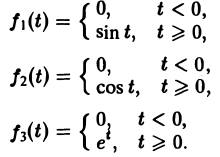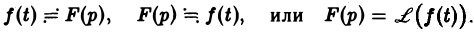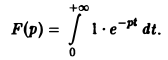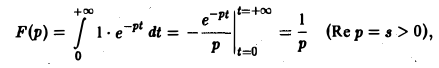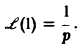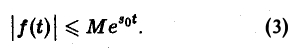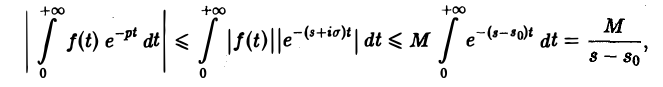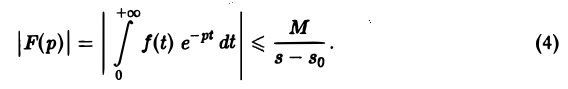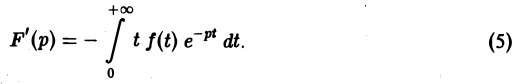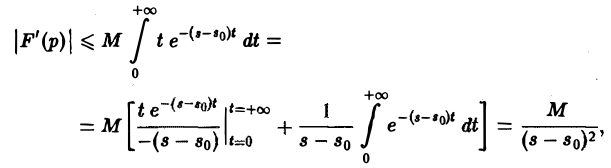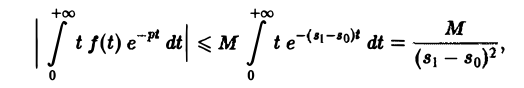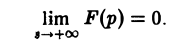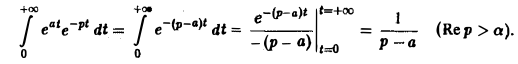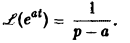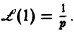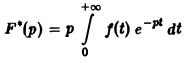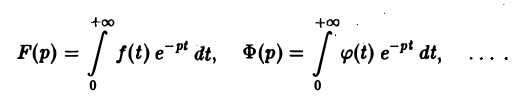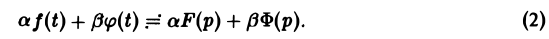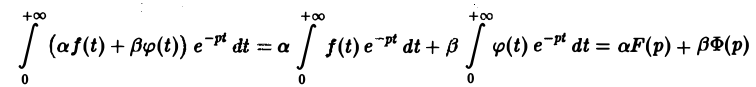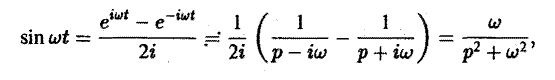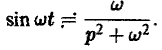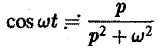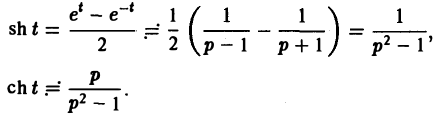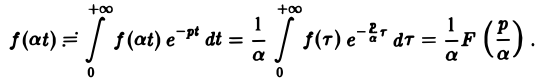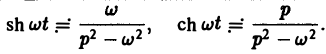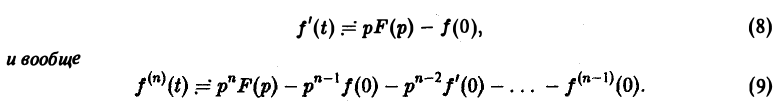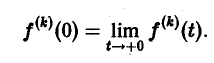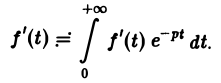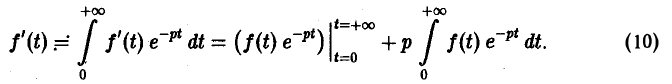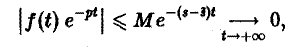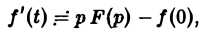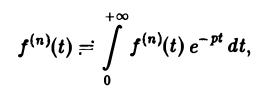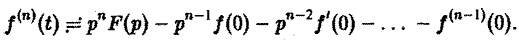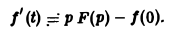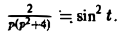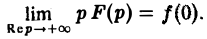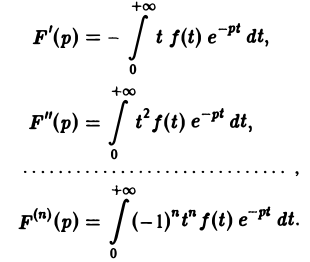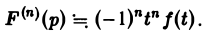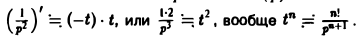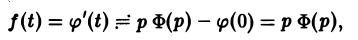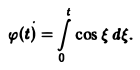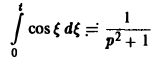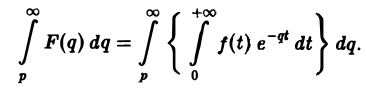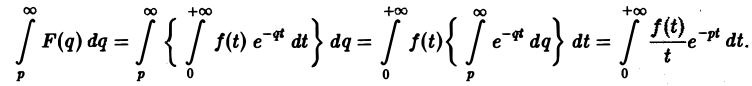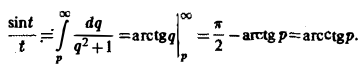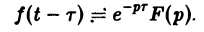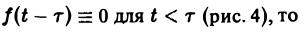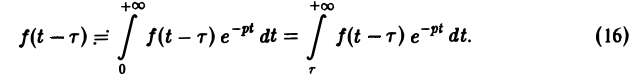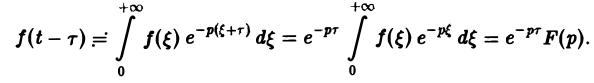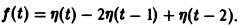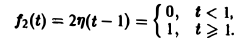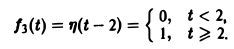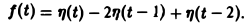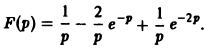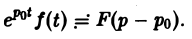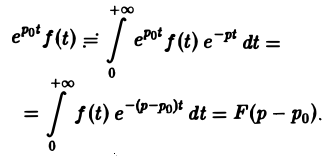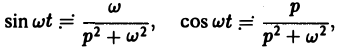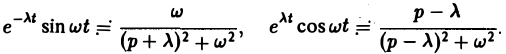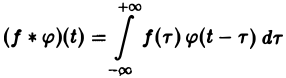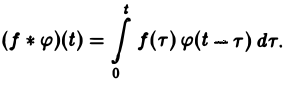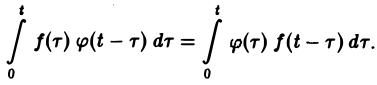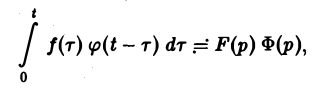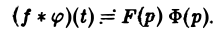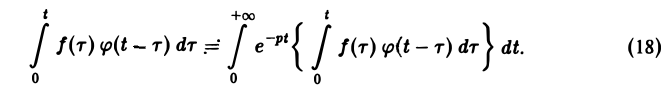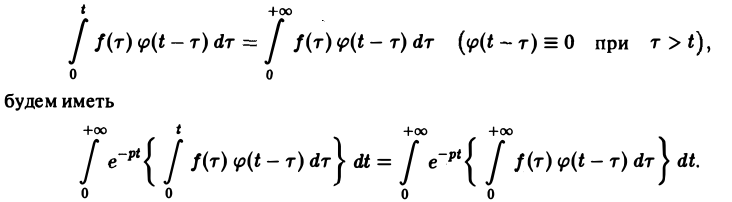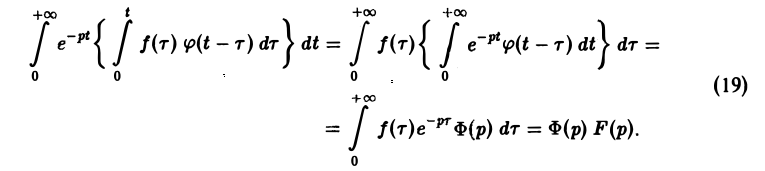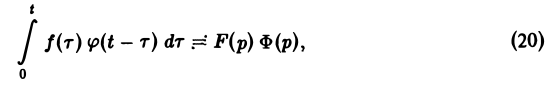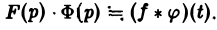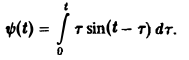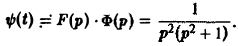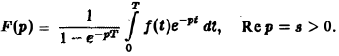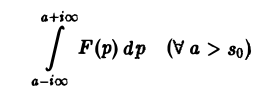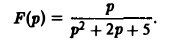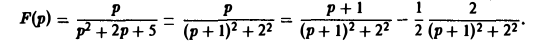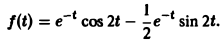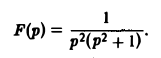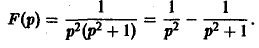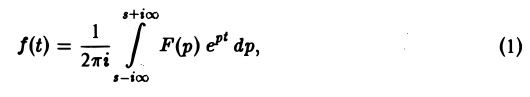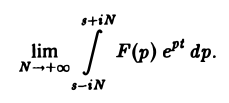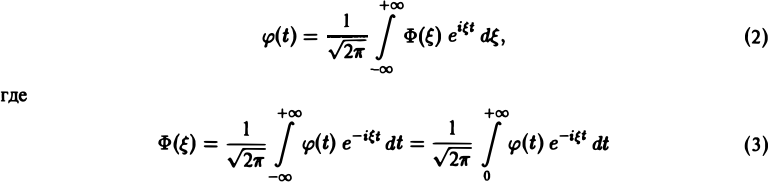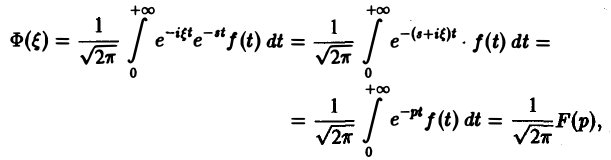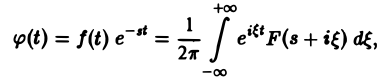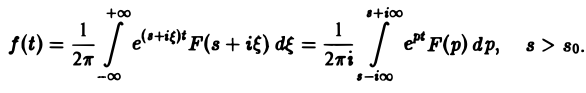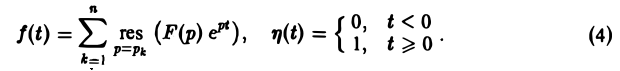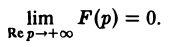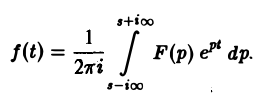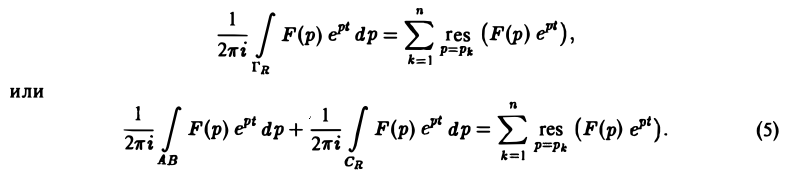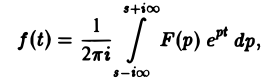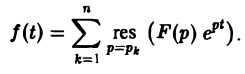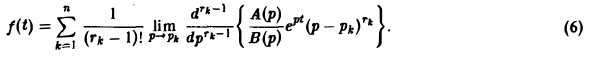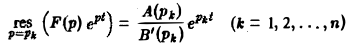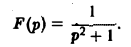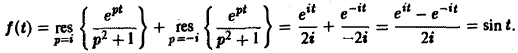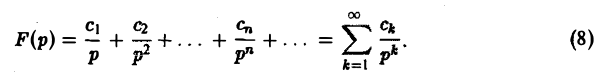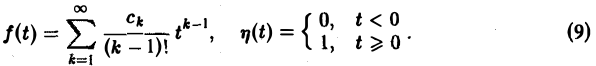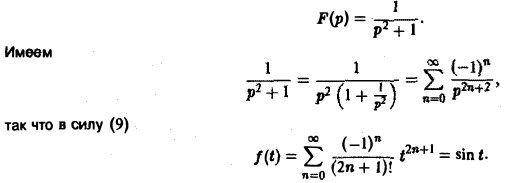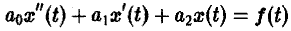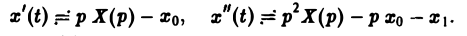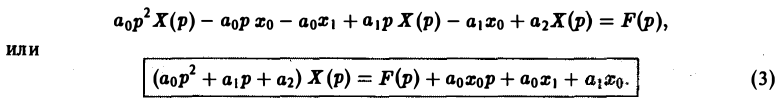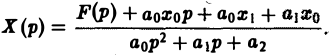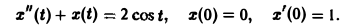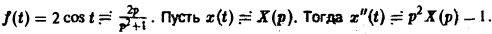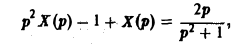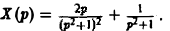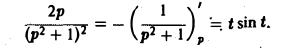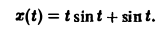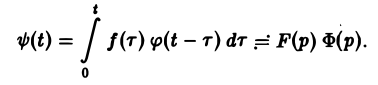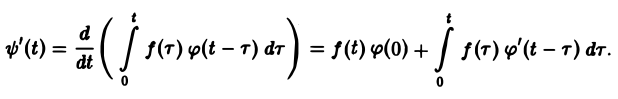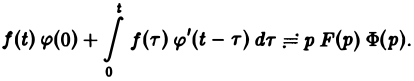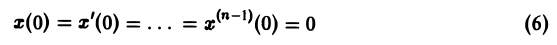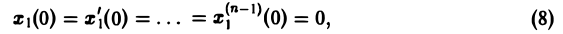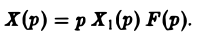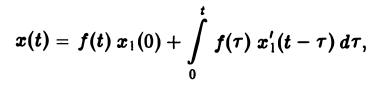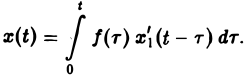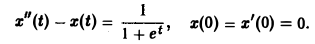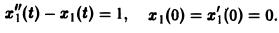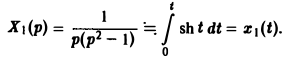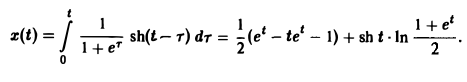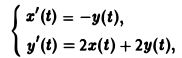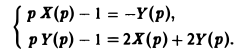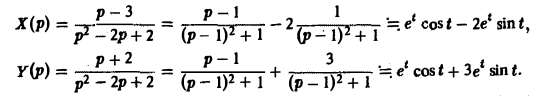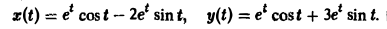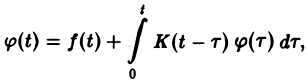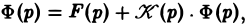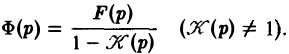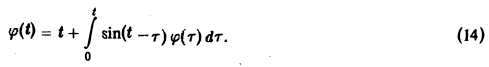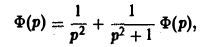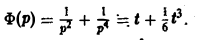Метод лапласа в решении уравнений

Ранее мы рассмотрели интегральное преобразование Фурье

с ядром K(t, ξ) = .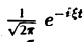

Преобразование Фурье неудобно тем, что должно быть выполнено условие абсолютной интегрируемости функции f(t) на всей оси t,

Преобразование Лапласа позволяет освободиться от этого ограничения.

Определение:

Функцией-оригиналом будем называть всякую комплекснозначную функцию f(t) действительного аргумента t, удовлетворяющую следующим условиям:

1. f(t) непрерывна на всей оси t, кроме отдельных точек, в которых f(t) имеет разрыв 1-го рода, причем на каждом конечном интервале оси t таких точек может быть лишь конечное число;
2. функция f(t) равна нулю при отрицательных значениях t, f(t) = 0 при t 0 и з такие, что для всех t

Ясно, что если неравенство (1) выполняется при некотором s = s1, то оно будет выполнятся при всяком s2 > s1.

Точная нижняя грань sо всех чисел s, so = infs, для которых выполняется неравенство (1), называется показателем роста функции f(t).

Замечание:

В общем случае неравенство

не имеет места, но справедлива оценка

где ε > 0 — любое. Так, функция f(t) = t, t ≥ 0, имеет показатель роста so =0. Для нее неравенство |t| ≤ М ∀t ≥ 0 не выполняется, но ∀ε > О, ∀t > 0 верно неравенство

Условие (1) гораздо менее ограничительное, чем условие (*).

Пример:

не удовлетворяет условию (*), но условие (1) выполнено при любом s ≥ 1 и М ≥ 1; показатель роста so = 1. Так что f(t) является функцией-оригиналом. С другой стороны, функция

не является функцией-оригиналом: она имеет бесконечный порядок роста, sо = +∞. Простейшей функцией-оригиналом является
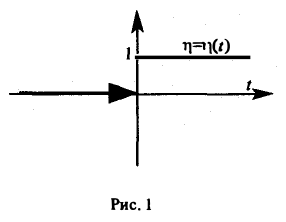
так называемая единичная функция

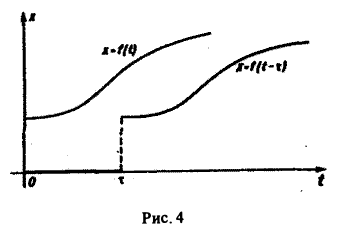
Если некоторая функция φ(t) удовлетворяет условиям 1 и 3 определения 1, но не удовлетворяет условию 2, то произведение f(t) = φ(t) η(t) уже является функцией-оригиналом.

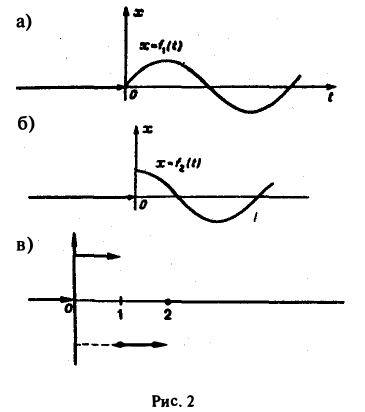
Для простоты записи мы будем, как правило, множитель η(t) опускать, условившись, что все функции, которые мы будем рассматривать, равны нулю для отрицательных t, так что если речь идет о какой-то функции f(t) например, о sin t, cos t, e t и т. д., то всегда подразумеваются следующие функции (рис. 2):

Определение:

Пусть f(t) есть функция-оригинал. Изображением функции f(t) по Лапласу называется функция F(p) комплексного переменного р = s + iσ, определяемая формулой

где интеграл берется по положительной полуоси t. Функцию F(p) называют также преобразованием Лапласа функции f(t); ядро преобразования K(t, р) = e -pt .
Тот факт, что функция f(x) имеет своим изображением F(p), будем записывать так:

Пример:

Найти изображение единичной функции η(t).

Функция 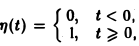является функцией-оригиналом с показателем роста s0 = 0. В силу формулы (2) изображением функции η(t) будет функция

Если р = s + iσ, то при s > 0 интеграл в правой части последнего равенства будет сходящимся, и мы получим

так что изображением функции η(t) будет функция 1/p. Как мы условились, будем писать, что η(t) = 1, и тогда полученный результат запишется так:

Теорема:

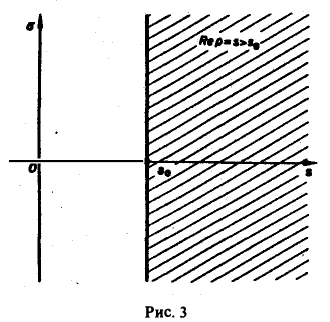
Для всякой функции-оригинала f(t) с показателем роста sо изображение F(p) определено в полуплоскости Re p = s > So и является в этой полуплоскости аналитической функцией (рис. 3).

Для доказательства существования изображения F(p) в указанной полуплоскости достаточно установить, что несобственный интеграл (2) абсолютно сходится при s > so. Используя (3), получаем

что и доказывает абсолютную сходимость интеграла (2). Одновременно мы получили оценку преобразования Лапласа F(p) в полуплоскости сходимости Re р = s > so

Дифференцируя выражение (2) формально под знаком интеграла по р, находим

Существование интеграла (5) устанавливается так же, как было установлено существование интеграла (2).

Применяя для F'(p) интегрирование по частям, получаем оценку

откуда следует абсолютная сходимость интеграла (5). (Внеинтегральное слагаемое 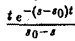— при t → + ∞ имеет предел, равный нулю). В любой полуплоскости Re р ≥ S1 > So интеграл (5) сходится равномерно относительно р, поскольку он мажорируется сходящимся интегралом

не зависящим от р. Следовательно, дифференцированиепо р законно и равенство (5) справедливо.

Поскольку производная F'(p) существует, преобразование Лапласа F(p) всюду в полуплоскости Re p = s > sо является аналитической функцией.

Из неравенства (4) вытекает

Следствие:

Если точка р стремится к бесконечности так, что Re р = s неограниченно возрастает, то

Пример:

Найдем еще изображение функции f(t) =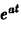, где а = а + iβ — любое комплексное число.

Показатель роста sо функции f(t) равен а.

Считая Rep = s> а, получим

При а = 0 вновь получаем формулу

Обратим внимание на то, что изображение функции 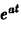является аналитической функцией аргумента р не только в полуплоскости Re p > а, но и во всех точках р, кроме точки р = а, где это изображение имеет простой полюс. В дальнейшем мы не раз встретимся с подобной ситуацией, когда изображение F(p) будет аналитической функцией во всей плоскости комплексного переменного р, за исключением изолированных особых точек. Противоречия с теоремой 1 нет. Последняя утверждает лишь, что в полуплоскости Re p > So функция F(p) не имеет особых точек: все они оказываются лежащими или левее прямой Re p = So, или на самой этой прямой.

Замечание:

В операционном исчислении иногда пользуются изображением функции f(t) по Хевисайду, определяемым равенством

и отличаюикмся от шоСражения по Лапласу множителем р.

Видео:7.1 Решение уравнения Лапласа в прямоугольникеСкачать

Свойства преобразования Лапласа

В дальнейшем через f(t), φ(t), … будем обозначать функции-оригиналы, а через F(p), Ф(р), … — их изображения по Лапласу,

Из определения изображения следует, что если f(t) = 9 ∀t, то F(p) = 0.

Теорема единственности:

Теорема:

Справедливость утверждения вытекает из свойства линейности интеграла, определяющего изображение:

— показатели роста функций f(t) и φ(t) соответственно).

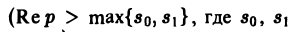
На основании этого свойства получаем

Аналогично находим, что
(4)

Теорема подобия:

Если f(t) — функция-оригинал и F(p) — ее изображение по Лапласу, то для любого постоянного а > 0

Полагая at = т, имеем

Пользуясь этой теоремой, из формул (5) и (6) получаем

Теорема:

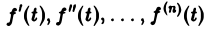
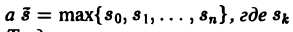
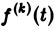
О дифференцировании оригинала. Пусть f(t) является функцией-оригиналом с изображением F(p) и пусть — также функции-оригиналы, — показатель роста функции (k = 0, 1,…, п). Тогда

Здесь под fk(0) (k = 0,1,… , п — 1) понимается правое предельное значение .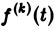

Пусть f(t) = F(p). Найдем изображение f'(t). Имеем

Интегрируя по частям, получаем

Внеинтегральное слагаемое в правой части (10) обращается в нуль при t → + ∞, т. к. при Re р = s > 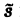имеем

подстановка t = 0 дает -f(0).

Второе слагаемое справа в (10) равно pF(p). Таким образом, соотношение (10) принимаетвид

и формула (8) доказана. В частности, если f(0) = 0, то f'(t) = pF(p). Для отыскания изображения 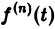запишем

откуда, интегрируя п раз по частям, получим

Пример:

Пользуясь теоремой о дифференцировании оригинала, найти изображение функции f(t) = sin 2 t.

Пусть f(t) = F(p). Тогда

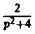
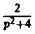
Но f(0) = О, а f'(0) = 2 sin t cos t = sin 2t = . Следовательно, = pF(p), откуда F(p) =

Теорема 5 устанавливает замечательное свойство интегрального преобразования Лапласа: оно (как и преобразование Фурье) переводит операцию дифференцирования в алгебраическую операцию умножения на р.

Формула включения. Если f(t) и f'(t) являются функциями-оригиналами, то (11)

В самом деле, f'(

Так как функция F(p) в полуплоскости Rep = s > so является аналитической, то ее можно дифференцировать по р. Имеем

Последнее как раз и означает, что

Пример:

Пользуясь теоремой 6, найти изображение функции .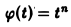

Как известно, 1 = 1/p. Здесь f(t) = 1, F(p) = 1/p. Отсюда (1/p)’= (-t) • 1, или 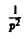= t. Вновь применяя теорему 6, найдем

Теорема:

Интегрирование оригинала. Интегрирование оригинала сводится к делению изображения на р: если f(t) = F(p), то

Нетрудно проверить, что если f(t) есть функция-оригинал, то и φ(t) будет функцией-оригиналом, причем φ(0) = 0. Пусть φ(t) = Ф(р). В силу (14)

С другой стороны, f(t) =’ F(p), откуда F(p) = рФ(р), т.е. Ф(р) =.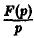

Последнее равносильно доказываемому соотношению (13).

Пример:

Найти изображение функции

В данном случае f(t) = cos t, так что F(p) = 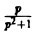. Поэтому

Теорема:

Интегрирование изображения. Если f(t) = F(p) и интеграл 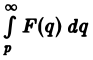сходится, то он служит изображением функции

Предполагая, что путь интегрирования (р, ∞) лежит в полуплоскости Re p ≥ а> so, мы можем изменить порядок интегрирования (t > 0):

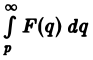
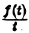
Последнее равенство означает, что является изображением функции .

Пример:

Найти изображение функции .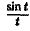

Как известно, sin t = .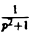

Теорема запаздывания:

Положим ξ = t- τ. Тогда dt = d ξ. При t = τ получаем ξ = 0, при t = + ∞ имеем ξ = + ∞.

Поэтому соотношение (16) принимает вид

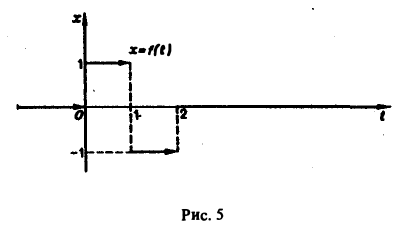
Пример:

Найти изображение функции f(t), заданной графически (рис. 5).

Запишем выражение для функции f(t) в следующем виде:

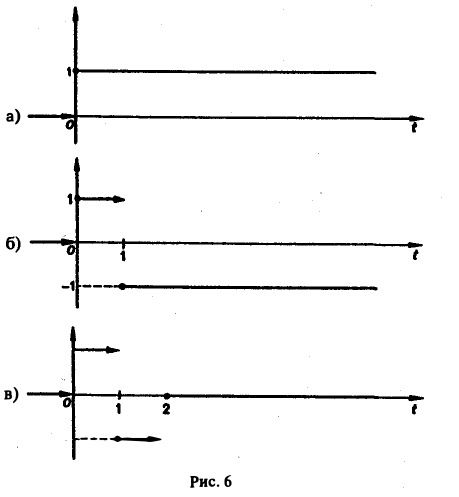
Это выражение можно получить так. Рассмотрим функцию f1(t) = η(t) для t ≥ 0 (рис. 6 а) и вычтем из нее функцию

Разность f(t) — h(t) будет равна единице для t ∈ [0,1) и -1 для t ≥ 1 (рис. 6 b). К полученной разности прибавим функцию

В результате получим функцию f(t) (рис. 6 в), так что

Отсюда, пользуясь теоремой запаздывания, найдем

Теорема смещения:

Теорема позволяет по известным изображениям функций находить изображения тех же функций, умноженных на показательную функцию 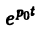, например,

Свертка функций. Теорема умножения

Пусть функции f(t) и φ(t) определены и непрерывны для всех t. Сверткой (f *φ)(t) этих функций называется новая функция от t, определяемая равенством

(если этот интеграл существует).

Для функций-оригиналов f(t) и φ(t) операция свертки всегда выполнима, причем
(17)

В самом деле, произведение функций-оригиналов f( τ ) φ(t — τ), как функция от τ, является финитной функцией, т.е. обращается в нуль вне некоторого конечного промежутка (в данном случае вне отрезка 0 ≤ τ ≤ t). Для финитных непрерывных функций операция свертки выполнима, и мы получаем формулу (17).

Нетрудно проверить, что операциясвертки коммутативна,

Теорема умножения:

Нетрудно проверить, что свертка (f * φ)(t) функций-оригиналов есть функция-оригинал с показателем роста s* = mах, где s1, s2

показатели роста функций f(t) и φ(t) соответственно. Найдем изображение свертки,

Воспользовавшись тем, что

Меняя порядок интегрирования в интеграле справа (при Re р = s > s* такая операция законна) и применяя теорему запаздывания, получим

Таким образом, из (18) и (19) находим

— умножению изображений отвечает свертывание оригиналов,

Пример:

Найти изображение функции

Функция ψ(t) есть свертка функций f(y) = t и φ(t) = sin t. В силу теоремы умножения

Задача:

Пусть функция f(t), периодическая с периодом Т, есть функция-оригинал. Показать, что ее изображение по Лапласу F[p) дается формулой

Видео:Преобразование Лапласа Решение системы линейных дифференциальных уравненийСкачать

Отыскание оригинала по изображению

Задача ставится так: дана функция F(p), надо найти функцию f(t). изображением которой является F(p).

Сформулируем условия, достаточные для того, чтобы функция F(p) комплексного переменного р служила изображением.

Теорема:

Если аналитическая в полуплоскости Rep = s > so функция F(p)

1) стремится к нулю при |р| —» + ∞ в любой полуплоскости Re р = а > So равномерно относительно arg р;

сходится абсолютно, то F(p) является изображением некоторой функции-оригинала f<t).

Задача:

Может ли функция F(p) = 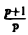служить изображением некоторой функции-оригинала? Укажем некоторые способы отыскания оригинала по изображению.

Отыскание оригинала с помощью таблиц изображений

Прежде всего стоит привести функцию F(p) к более простому, «табличному» виду. Например, в случае, когда F(p) — дробно-рациональная функция аргумента р,ее разлагают на элементарные дроби и пользуются подходящими свойствами преобразования Лапласа.

Пример:

Найти оригинал для

Запишем функцию F(p) в виде:

Пользуясь теоремой смещения и свойством линейности преобразования Лапласа, получаем

Пример:

Найти оригинал для функции

Запишем F(p) в виде

Отсюда f(t) = t — sin t.

Использование теоремы обращения и следствий из нее

Теорема обращения:

где интеграл берется вдоль любой прямой Re p = s > So и понимается в смысле главного значения, т. е. как

Формула (1) называется формулой обращения преобразования Лапласа, или формулой Меллина. В самом деле, пусть, например, f(t) — кусочно-гладкая на каждом конечном отрезке [0, а] функция-оригинал-с показателем роста so. Рассмотрим функцию φ(t) = 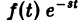, где s>so — любое.

Функция φ(t) удовлетворяет условиям применимости интегральной формулы Фурье, и, следовательно, справедлива формула обращения преобразования Фурье,

(φ(t) ≡ 0 при t

откуда получаем формулу обращения преобразования Лапласа

Как следствие из теоремы обращения получаем теорему единственности.

Теорема:

Две непрерывные функции f(t) и φ(t), имеющие одно и то же изображение F(p), тождественны.
Непосредственное вычисление интеграла обращения (1) обычно затруднительно. Отыскание оригинала по изображению упрощается при некоторых дополнительных ограничениях на F(p).

Теорема:

Пусть изображение F(p) — дробно-рациональная функция с полюсами р1, p2….pп. Тогда оригиналом для F(p) будет функция f(t) η(t), где

Пусть изображение F(p) — дробно-рациональная функция, F(p) = 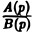, где А(р), В(р) — многочлены относительно р (взаимно простые), причем степень числителя А(р) меньше степени знаменателя В(р), т. к. для всякого изображения должно выполняться предельное соотношение

Пусть корни знаменателя В(р), являющиеся полюсами изображения F(p), суть р1, р2, …, рп, а их кратности равны r1, r2, …, rп соответственно.

Если число s, фигурирующее в формуле (1), взять большим всех Re pk (k = 1,2,…, п), то по формуле обращения, которая в этих условиях применима, получим

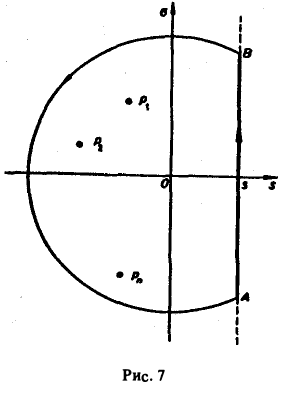
Рассмотрим замкнутый контур ГR (рис.7), состоящий из дуги CR окружности радиуса R с центром в начале координат и стягивающей ее хорды АВ (отрезка прямой Re р = s), и проходимый в положительном направлении, причем радиус R настолько велик, что все полюсы F(p) лежат внутри ГR.

По теореме Коши о вычетах при любом R, удовлетворяющем указанному условию, будем иметь

Второе слагаемое слева в равенстве (5) стремится к нулю при R → ∞. Это следует из леммы Жордана, если в ней заменить р на iz и учесть, что F(p) → 0 при Re p → + ∞. Переходя в равенстве (5) к пределу при R → ∞, мы получим слева

а справа — сумму вычетов по всем полюсам функции F(p)

Замечание:

Воспользовавшись формулой для вычисления вычетов, найдем, что

Если все полюсы p1, р2,…, рn — простые, то

и формула (6) принимает вид

Пример:

Найти оригинал для функции

Функция F(p) имеет простые полюсы р1 = i. p2 = -i. Пользуясь формулой (7), находим

Теорема:

Пусть изображение F(p) является аналитической функцией в бесконечно удаленной точке р = ∞, причем ее разложение в окрестности |р| > R бесконечно удаленной точки имеет вид

Тогда оригиналом для F(p) будет функция f(t) η<t), где

Пример:

Видео:Метод Лапласа решения ДУСкачать

Приложения преобразования Лапласа (операционного исчисления)

Решение линейных дифференциальных уравнений с постоянными коэффициентами

Дано линейное дифференциальное уравнение второго порядка с постоянными коэффициентами
(1)

(ао, а1, а2 — действительные числа) и требуется найти решение уравнения (1) для t > 0, удовлетворяющее начальным условиям

Будем считать, что f(t) есть функция-оригинал. Тогда x(t) — также функция-оригинал. Пусть

f(t) = F(p), x(t) = X(p).

По теореме о дифференцировании оригинала имеем

Перейдем в уравнении (1) от оригиналов к изображениям. Имеем

Это уже не дифференциальное, а алгебраическое уравнение относительно изображения Х(р) искомой функции. Его называют операторным уравнением. Решая его, найдем операторное решение задачи (1)-(2) —

Оригинал для Х(р) будет искомым решением х(t) задачи (1)-(2).

Общий случай линейного дифференциального уравнения n-го порядка (n ≥ 1) с постоянными коэффициентами от случая п = 2 принципиально ничем не отличается.

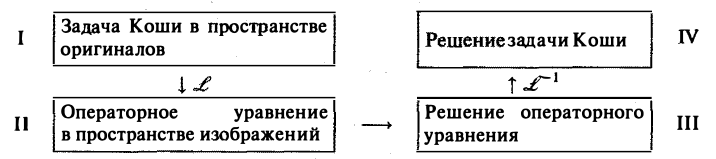
Приведем общую схему решения задачи Коши

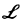
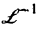
Здесь означает применение к 1 преобразование Лапласа, — применение к III обратного преобразования Лапласа.

Пример:

Решить задачу Коши

По теореме о дифференцировании изображения

Формула Дюамеля

В приложениях операционного исчисления к решению дифференциальных уравнений часто пользуются следствием из теоремы умножения, известным под названием формулы Дюамеля.

Пусть f(t) и φt) — функции-оригиналы, причем функция f(t) непрерывна на [0, + ∞), a φ(t) — непрерывно дифференцируема на [0,+ ∞). Тогда если f(t) = F(p), φ<t) = Ф(р),то по теореме умножения получаем, что

Нетрудно проверить, что функция ψ(t) непрерывно дифференцируема на [0, + ∞), причем

Отсюда, в силу правила дифференцирования оригиналов, учитывая, что ψ(0) = 0, получаем формулу Дюамеля
(4)

Покажем применение этой формулы.

Пусть требуется решить линейное дифференциальное уравнение n-го порядка (n ≥ 1) с постоянными коэффициентами

при нулевых начальных условиях

(последнее ограничение несущественно: задачу с ненулевыми начальными условиями можно свести к задаче с нулевыми условиями заменой искомой функции).

Если известно решение x(t) дифференциального уравнения с той же левой частью и правой частью, равной единице,

L[x(t)] = l (7)

при нулевых начальных условиях

то формула Дюамеля (4) позволяет сразу получить решение исходной задачи (5)-(6).

В самом деле, операторные уравнения, отвечающие задачам (5)-(6) и (7)-(8), имеют соответственно вид

где F(p) — изображение функции f(t). Из (9) и (10) легко находи

Отсюда по формуле Дюамеля

или, поскольку x1(0) = 0, (11)

Пример:

Решить задачу Коши

Рассмотрим вспомогательную задачу

Применяя операционный метод, находим

По формуле (11) получаем решение x(t) исходной задачи:

Интегрирование систем линейных дифференциальных уравнений с постоянными коэффициентами

Интегрирование систем осуществляется так же, как и решение одного линейного дифференциального уравнения — путем перехода от системы дифференциальных уравнений к системе операторных уравнений. Решая последнюю как систему линейных алгебраических уравнений относительно изображений искомых функций, получаем операторное решение системы. Оригинал для негобудетрешением исходной системы дифференциальных уравнений.

Пример:

Найти решение линейной системы

удовлетворяющее начальным условиям х(0) = у(0) = I.

Пусть х(

Решая последнюю относительно Х(р) и У(р), получаем

Решение исходной задачи Коши

Решение интегральных уравнений

Напомним, что интегральным уравнением называют уравнение, в котором неизвестная функция входит под знак интеграла. Мы рассмотрим лишь уравнение вида (12)

называемое линейным интегральным уравнением Вольтерра второго рода с ядром K(t — т), зависящим от разности аргументов (уравнение типа свертки). Здесь φ(t) — искомая функция, f(t) и K(t) — заданные функции.

Пусть f(t) и K(t) есть функции-оригиналы, f(t) =’ F(p), K(t) =’ K(p).

Применяя к обеим частям (12) преобразование Лапласа и, пользуясь теоремой умножения, получим
(13)

где Ф(р) = φ(t). Из (13)

Оригинал для Ф(р) будет решением интегрального уравнения (12).

Пример:

Решить интегральное уравнение

Применяя преобразование Лапласа к обеим частям (14), получим

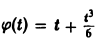
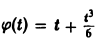
Функция является решением уравнения (14) (подстановка в уравнение (14) обращает последнее в тождество по t).

Замечание:

Преобразование Лапласа может быть использовано также при решении некоторых задач для уравнений математической физики.

Видео:Преобразование Лапласа - bezbotvyСкачать

Таблица преобразования Лапласа

Видео:Задача Дирихле для круга. Уравнение ЛапласаСкачать

Дополнение к преобразованию Лапласа

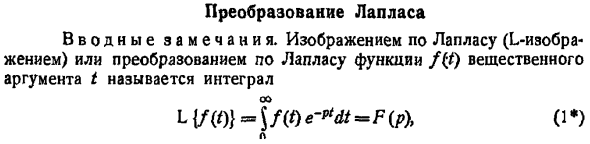
Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Видео:Преобразование Лапласа по определениюСкачать

Применение преобразования Лапласа к решению
линейных дифференциальных уравнений и систем

Видео:Вычисление определителя четвертого порядка по теореме ЛапласаСкачать

1°. Общие сведения о преобразовании Лапласа: оригинал и изображение

Функцией-оригиналом называется комплекснозначная функция действительного переменного , удовлетворяющая следующим условиям:

2) функция интегрируема на любом конечном интервале оси ;

3) с возрастанием модуль функции растет не быстрее некоторой показательной функции, т. е. существуют числа 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADoAAAAQBAMAAAC1onFLAAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAD3RSTlMAgUHAYqEh5RGR0VIxELEI83NdAAABBklEQVQY02NgIAAcBRWA5EVBMVRhDjUwdfq/AZCc/kUBVXa6sC2IYjNfwMDANN8AVZKxguExiGYR/sDAwOcvAGK7XIDJsgcw7D8ApFlVfzAwCM0HG8yysAEqe16AQR+kgZ3xEwNbwHqIIMvKBAgDaJY+yLJklt8MfB2foXpYTCHS8gIM+SBZR6aPDFu4P8IsZDI9AJXtB8kGsX3leMD5Ce5aJuMDEFmwyQUMnzkTuD4gZIORZNkMGJYrQkyBmgx2PdDB+hOAzhBgsDdg2C8AleSGuqp9AsP+DQwMXQIMQL/GQ8ORZSnUR5y1DOFA3/7/zyDJsB5IooYG7yvXGoz4aoAzeYQYGADRdjuTYajQpgAAAABJRU5ErkJggg==» /> и такие, что для всех имеем

Изображением функции-оригинала по Лапласу называется функция комплексного переменного , определяемая равенством

при s_0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAFIAAAATBAMAAADxBkdhAAAAKlBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAHrpZrAAAADXRSTlMAQcCBEFor0KCR6LBxSK9m8wAAAVlJREFUKM9jYCAaJBsbGx8jSqVj71LRWVuIUiqrwMB6iViVDHcT0AQNcaoUQBN0LsVh+3UGBlYlVSAnqUVaFarUASrPuKkFprJQ8JQKA0NUQmwAA0vBpZZciPnOxVClUQmzYSoXW1xyYGC7ycBewMB65DYD7waIOCtUaTHDDQY2EajtQMR8WVD6AgNj6lUGXgWoEawVYKWrpiYw9AglQFSyX2PgvGFsbMDAwHmFQXYDTKUGWOXZuwVsC1gVICqZ7jAw3wHLAl1gGwBVWAkOOja38IvMCowXoCpvMrDdYGAAKvGdwLAKotAV6szYCYzXgCovglQWMHBcZ1OYlcDWABRX4FmG6vVTCcwKTGCVsnfvKrDUWgQwX9oElJvb0ZSAGvJOmzUcOCFmgkP3IBCDDClngxjVipSEGBig7kQGLDexJg2g3zegCfFcxZ6KZoSjJ6FJShOwGwqMIwCRZlRL/vuSSQAAAABJRU5ErkJggg==» style=»vertical-align: middle;» />. Условие 3 обеспечивает существование интеграла (2).

Преобразование (2), ставящее в соответствие оригиналу его изображение , называется преобразованием Лапласа. При этом пишут .

Видео:Неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами МЕТОДОМ ЛАПЛАСАСкачать

Свойства преобразования Лапласа

Всюду в дальнейшем считаем, что

I. Свойство линейности. Для любых комплексных постоянных и

II. Теорема подобия. Для любого постоянного 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADEAAAAQBAMAAABNQoq8AAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAAcGe2BFbQSGBMfCxcU2qjNsAAADDSURBVBjTY2AgDYgvxCHB5WyyALtM9wW2HUhcDgs4006A8TGyyprjAlCWiwCjCpDNekkzACLQrA6RYnwkwKgHZK42DVFghkq5CcBlAhi4NjOwPSuGGtMJlmJ/xMCgV8DA9JSB6yXc8kg3IMEKkelTAOo2gMv4Iuypm8DA+DoArgVkGiPQbdpgGdY3DDAXQP3DAPKPiAFjkRMbiqsZ1iWwPweGkY+RafYxEL8IJsHA5jklAeSShQysIHtYEaHD2JbKwAAA/gYrl5lLD9QAAAAASUVORK5CYII=» />

III. Дифференцирование оригинала. Если есть оригинал, то

Обобщение: если раз непрерывно дифференцируема на и если есть оригинал, то

IV. Дифференцирование изображения равносильно умножению оригинала на «минус аргумент», т.е.

V. Интегрирование оригинала сводится к делению изображения на

VI. Интегрирование изображения равносильно делению на оригинала:

(предполагаем, что интеграл сходится).

VII. Теорема запаздывания. Для любого положительного числа

VIII. Теорема смещения (умножение оригинала на показательную функцию). Для любого комплексного числа

IX. Теорема умножения (Э. Борель). Произведение двух изображений и также является изображением, причем

Интеграл в правой части (14) называется сверткой функций и и обозначается символом

Теорема XI утверждает, что умножение изображений равносильно свертыванию оригиналов , т.е.

Видео:Пример вычисления определителя четвертого порядка по теореме ЛапласаСкачать

Отыскание оригиналов дробно-рациональных изображений

Для нахождения оригинала по известному изображению , где есть правильная рациональная дробь, применяют следующие приемы.

1) Эту дробь разлагают на сумму простейших дробей и находят для каждой из них оригинал, пользуясь свойствами I–IX преобразования Лапласа.

2) Находят полюсы этой дроби и их кратности . Тогда оригиналом для будет функция

где сумма берется по всем полюсам функции .

В случае, если все полюсы функции простые, т.е. , последняя формула упрощается и принимает вид

Пример 1. Найти оригинал функции , если

Решение. Первый способ. Представим в виде суммы простейших дробей

и найдем неопределенные коэффициенты . Имеем

Полагая в последнем равенстве последовательно , получаем

Находя оригиналы для каждой из простейших дробей и пользуясь свойствам линейности, получаем

Второй способ. Найдем полюсы функции . Они совпадают с нулями знаменателя . Таким образом, изображение имеет четыре простых полюса . Пользуясь формулой (17), получаем оригинал

Пример 2. Найти оригинал , если .

Решение. Данная дробь имеет полюс кратности и полюс кратности . Пользуясь формулой (16), получаем оригинал

Видео:Лекция 124. Преобразование Лапласа. ВведениеСкачать

2°. Решение задачи Коши для линейных дифференциальных уравнений с постоянными коэффициентами

Пусть требуется найти решение дифференциального уравнения второго порядка с постоянными коэффициентами

Будем считать, что функция и решение вместе с его производньь ми до второго порядка включительно являются функциями-оригиналами. Пусть . По правилу дифференцирования оригиналов с учетом (2) имеем

Применяя к обеим частям (1) преобразование Лапласа и пользуясь свойством линейности преобразования, получаем операторное уравнение

Решая уравнение (20), найдем операторное решение

Находя оригинал для , получаем решение уравнения (18), удовлетворяющее начальным условиям (19).

Аналогично можно решить любое уравнение n-го порядка с постоянными коэффициентами и с начальными условиями при .

Пример 3. Решить дифференциальное уравнение операторным методом

Решение. Пусть , тогда по правилу дифференцирования оригинала имеем

Известно, что поэтому, переходя отданной задачи (21)–(22) к операторному уравнению, будем иметь

Легко видеть, что функция удовлетворяет данному уравнению и начальному условию задачи.

Пример 4. Решить уравнение .

Решение. Так как и по условию , то операторное уравнение будет иметь вид

Отсюда находим операторное решение

Разлагаем правую часть на элементарные дроби:

Переходя к оригиналам, получаем искомое решение .

Пример 5. Решить уравнение .

Решение. Так как и по условию , то операторное уравнение будет иметь вид

и, следовательно, операторное решение

Разложим правую часть на элементарные дроби:

Переходя к оригиналам, получим решение поставленной задачи

Видео:OTAROVA JAMILA МЕТОД ФУРЬЕ РЕШЕНИЯ КРАЕВОЙ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА В ПРЯМОУГОЛЬНОЙСкачать

3°. Решение систем линейных дифференциальных уравнений с постоянными коэффициентами

Пусть требуется найти решение системы двух уравнений с постоянными коэффициентами

удовлетворяющее начальным условиям

Будем предполагать, что функции , а также и являются функциями-оригиналами.

По правилу дифференцирования оригиналов с учетом (24) имеем

Применяя к обеим частям каждого из уравнений системы (23) преобразование Лапласа, получим операторную систему

Эта система является линейной алгебраической системой двух уравнений с двумя неизвестными и . Решая ее, мы найдем и , а затем, переходя к оригиналам, получим решение системы (23), удовлетворяющее начальным условиям (24). Аналогично решаются линейные системы вида

Пример 6. Найти решение системы дифференциальных уравнений операторным методом

удовлетворяющее начальному условию .

Решение. Так как и , то операторная система будет иметь вид

Решая систему, получаем

Разлагаем дроби, стоящие в правых частях, на элементарные:

Переходя к оригиналам, получим искомое решение

Видео:Решение уравнения Лапласа в шареСкачать

Символьное решение линейных дифференциальных уравнений и систем методом преобразований Лапласа c применением SymPy

Реализация алгоритмов на языке Python с использованием символьных вычислений очень удобна при решении задач математического моделирования объектов, заданных дифференциальными уравнениями. Для решения таких уравнений широко используются преобразования Лапласа, которые, говоря упрощенно, позволяют свести задачу к решению простейших алгебраических уравнений.

В данной публикации предлагаю рассмотреть функции прямого и обратного преобразования Лапласа из библиотеки SymPy, которые позволяют использовать метод Лапласа для решения дифференциальных уравнений и систем средствами Python.

Сам метод Лапласа и его преимущества при решении линейных дифференциальных уравнений и систем широко освещены в литературе, например в популярном издании [1]. В книге метод Лапласа приведен для реализации в лицензионных программных пакетах Mathematica, Maple и MATLAB (что подразумевает приобретение учебным заведением этого ПО) на выбранных автором отдельных примерах.

Попробуем сегодня рассмотреть не отдельный пример решения учебной задачи средствами Python, а общий метод решения линейных дифференциальных уравнений и систем с использованием функций прямого и обратного преобразования Лапласа. При этом сохраним обучающий момент: левая часть линейного дифференциального уравнения с условиями Коши будет формироваться самим студентом, а рутинная часть задачи, состоящая в прямом преобразовании Лапласа правой части уравнения, будет выполняться при помощи функции laplace_transform().

История об авторстве преобразований Лапласа

Преобразования Лапласа (изображения по Лапласу) имеют интересную историю. Впервые интеграл в определении преобразования Лапласа появился в одной из работ Л. Эйлера. Однако в математике общепринято называть методику или теорему именем того математика, который открыл ее после Эйлера. В противном случае существовало бы несколько сотен различных теорем Эйлера.

В данном случае следующим после Эйлера был французский математик Пьер Симон де Лаплас (Pierre Simon de Laplace (1749-1827)). Именно он использовал такие интегралы в своей работе по теории вероятностей. Самим Лапласом не применялись так называемые «операционные методы» для нахождения решений дифференциальных уравнений, основанные на преобразованиях Лапласа (изображениях по Лапласу). Эти методы в действительности были обнаружены и популяризировались инженерами-практиками, особенно английским инженером-электриком Оливером Хевисайдом (1850-1925). Задолго до того, как была строго доказана справедливость этих методов, операционное исчисление успешно и широко применялось, хотя его законность ставилось в значительной мере под сомнение даже в начале XX столетия, и по этой теме велись весьма ожесточенные дебаты.

Функции прямого и обратного преобразования Лапласа

Эта функция возвращает (F, a, cond), где F(s) есть преобразование Лапласа функции f(t), a Текст программы

Время на обратное визуальное преобразование Лапласа: 2.68 s

Обратное преобразование Лапласа часто используется при синтезе САУ, где Python может заменить дорогостоящих программных “монстров” типа MathCAD, поэтому приведенное использование обратного преобразования имеет практическое значение.

Преобразование Лапласа от производных высших порядков для решения задачи Коши

Если a и b — константы, то

для всех s, таких, что существуют оба преобразования Лапласа (изображения по Лапласу) функций f(t) и q(t).

Проверим линейность прямого и обратного преобразований Лапласа с помощью ранее рассмотренных функций laplace_transform() и inverse_laplace_transform(). Для этого в качестве примера примем f(t)=sin(3t), q(t)=cos(7t), a=5, b=7 и используем следующую программу.

(7*s**3 + 15*s**2 + 63*s + 735)/((s**2 + 9)*(s**2 + 49))
(7*s**3 + 15*s**2 + 63*s + 735)/((s**2 + 9)*(s**2 + 49))
True
5*sin(3*t) + 7*cos(7*t)
5*sin(3*t) + 7*cos(7*t)

Приведенный код также демонстрирует однозначность обратного преобразования Лапласа.

Если предположить, что удовлетворяет условиям первой теоремы, то из этой теоремы будет следовать, что:

Повторение этого вычисления дает

После конечного числа таких шагов мы получаем следующее обобщение первой теоремы:

Применяя соотношение (3), содержащее преобразованные по Лапласу производные искомой функции с начальными условиями, к уравнению (1), можно получить его решение по методу, специально разработанному на нашей кафедре при активной поддержке Scorobey для библиотеки SymPy.

Метод решения линейных дифференциальных уравнений и систем уравнений, основанный на преобразованиях Лапласа, с использованием библиотеки SymPy

где — приведенное начальное положение массы, — приведенная начальная скорость массы.

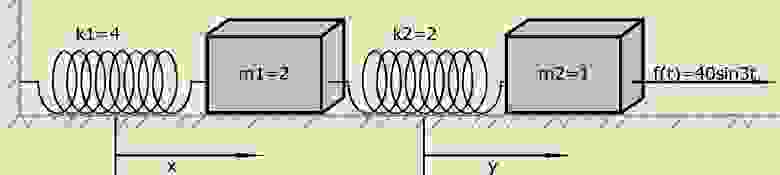
Упрощённая физическая модель, заданная уравнением (4) при ненулевых начальных условиях [1]:

Система, состоящая из материальной точки заданной массы, закрепленной на пружине, удовлетворяет задаче Коши (задаче с начальными условиями). Материальная точка заданной массы первоначально находится в покое в положении ее равновесия.

Для решения этого и других линейных дифференциальных уравнений методом преобразований Лапласа удобно пользоваться следующей системой, полученной из соотношений (3):

Последовательность решения средствами SymPy следующая:

загружаем необходимые модули и явно определяем символьные переменные:

указываем версию библиотеки sympy, чтобы учесть ее особенности. Для этого нужно ввести такие строки:

по физическому смыслу задачи переменная времени определяется для области, включающей ноль и положительные числа. Задаём начальные условия и функцию в правой части уравнения (4) с её последующим преобразование по Лапласу. Для начальных условий необходимо использовать функцию Rational, поскольку использование десятичного округления приводит к ошибке.

пользуясь (5), переписываем преобразованные по Лапласу производные, входящие в левую часть уравнения (4), формируя из них левую часть этого уравнения, и сравниваем результат с правой его частью:

решаем полученное алгебраическое уравнение относительно преобразования X(s) и выполняем обратное преобразование Лапласа:

осуществляем переход из работы в библиотеке SymPyв библиотеку NumPy:

строим график обычным для Python методом:

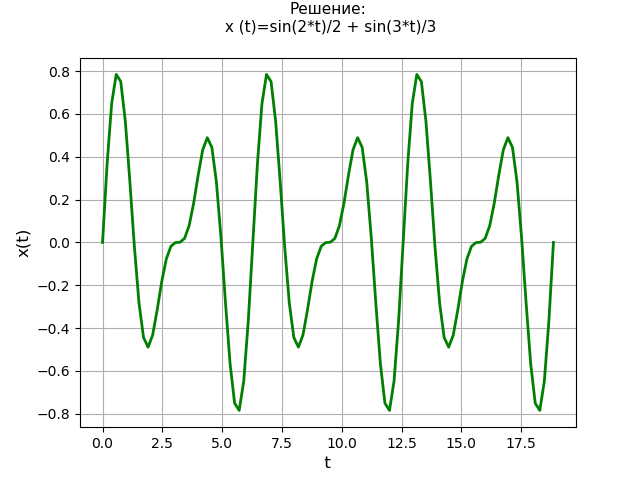
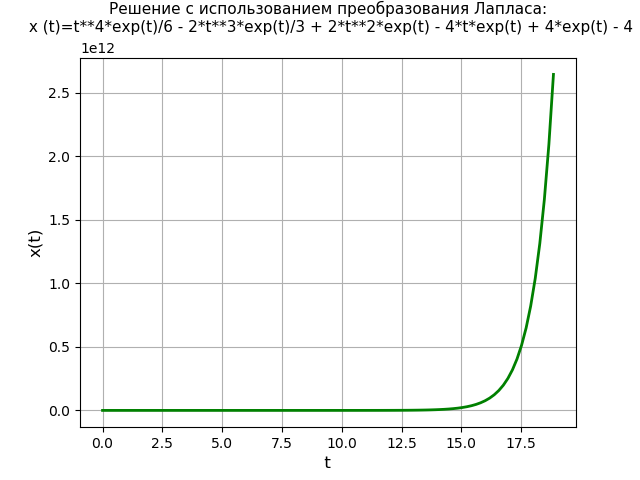
Получаем:
Версия библиотеки sympy – 1.3

Получен график периодической функции, дающей положение материальной точки заданной массы. Метод преобразования Лапласа с использованием библиотеки SymPy дает решение не только без потребности сначала найти общее решение однородного уравнения и частное решение первоначального неоднородного дифференциального уравнения, но и без потребности использования метода элементарных дробей и таблиц Лапласа.

При этом учебное значение метода решения сохраняется за счёт необходимости использования системы (5) и перехода в NumPy для исследования решения более производительными методами.

Для дальнейшей демонстрации метода решим систему дифференциальных уравнений:

с начальными условиями

Упрощённая физическая модель, заданная системой уравнений (6) при нулевых начальных условиях:

Таким образом, сила f(t) внезапно прилагается ко второй материальной точке заданной массы в момент времени t = 0, когда система находится в покое в ее положении равновесия.

Решение системы уравнений идентично ранее рассмотренному решению дифференциального уравнения (4), поэтому привожу текст программы без пояснений.

Для ненулевых начальных условий текст программы и график функций примет вид:

Рассмотрим решение линейного дифференциального уравнения четвёртого порядка с нулевыми начальными условиями:

Решим линейное дифференциальное уравнение четвёртого порядка:

с начальными условиями , , .

Функции для решения ОДУ

Для имеющих аналитическое решение ОДУ и систем ОДУ применяется функция dsolve():
sympy.solvers.ode.dsolve(eq, func=None, hint=’default’, simplify=True, ics=None, xi=None, eta=None, x0=0, n=6, **kwargs)

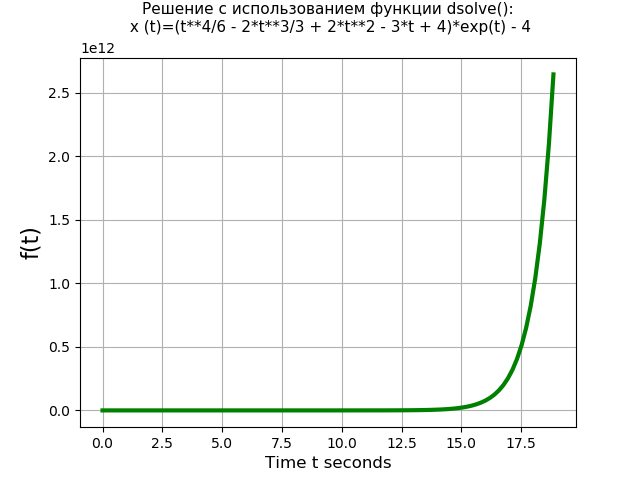
Давайте сравним производительность функции dsolve() с методом Лапласа. Для примера возьмём следующее дифференциальное уравнение четвёртой степени с нулевыми начальными условиями:

Время решения уравнения с использованием функции dsolve(): 1.437 s

Время решения уравнения с использованием преобразования Лапласа: 3.274 s

Итак, функция dsolve() (1.437 s) решает уравнение четвёртого порядка быстрее, чем выполняется решение по методу преобразований Лапласа (3.274 s) более чем в два раза. Однако при этом следует отметить, что функция dsolve() не решает системы дифференциальных уравнений второго порядка, например, при решении системы (6) с использованием функция dsolve() возникает ошибка:

Данная ошибка означает, что решение системы дифференциальных уравнений с помощью функции dsolve() не может быть представлено символьно. Тогда как при помощи преобразований Лапласа мы получили символьное представление решения, и это доказывает эффективность предложенного метода.

Для того чтобы найти необходимый метод решения дифференциальных уравнений с помощью функции dsolve(), нужно использовать classify_ode(eq, f(x)), например:

Eq(f(x), C1*sin(x) + C2*cos(x))
(‘nth_linear_constant_coeff_homogeneous’, ‘2nd_power_series_ordinary’)
(‘separable’, ‘1st_exact’, ‘almost_linear’, ‘1st_power_series’, ‘lie_group’, ‘separable_Integral’, ‘1st_exact_Integral’, ‘almost_linear_Integral’)
[Eq(f(x), -acos((C1 + Integral(0, x))*exp(-Integral(-tan(x), x))) + 2*pi), Eq(f(x), acos((C1 + Integral(0,x))*exp(-Integral(-tan(x), x))))]

Таким образом, для уравнения eq=Eq(f(x).diff(x,x)+f(x),0) работает любой метод из первого списка:

Для уравнения eq = sin(x)*cos(f(x)) + cos(x)*sin(f(x))*f(x).diff(x) работает любой метод из второго списка:

separable, 1st_exact, almost_linear,
1st_power_series, lie_group, separable_Integral,
1st_exact_Integral, almost_linear_Integral

Чтобы использовать выбранный метод, запись функции dsolve() примет вид, к примеру:

Вывод:

Данная статья ставила своей целью показать, как использовать средства библиотек SciPy и NumPy на примере решения систем линейных ОДУ операторным методом. Таким образом, были рассмотрены методы символьного решения линейных дифференциальных уравнений и систем уравнений методом Лапласа. Проведен анализ производительности этого метода и методов, реализованных в функции dsolve().

1. Дифференциальные уравнения и краевые задачи: моделирование и вычисление с помощью Mathematica, Maple и MATLAB. 3-е издание.: Пер. с англ. — М.: ООО «И.Д. Вильяме», 2008. — 1104 с.: ил. — Парал. тит. англ.
2. Использование обратного преобразования Лапласа для анализа динамических звеньев систем управления

🎬 Видео

Сеточные методы решения дифференциальных уравнений в частных производных.Скачать

Найти определитель матрицы 4x4Скачать

13. Операционное исчисление. Решить неоднородное ДУ 2 порядкаСкачать

2020 г. Операторный метод (Лапласа) для анализа цепей. Лекция и практикаСкачать

Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать