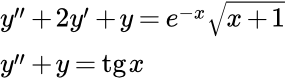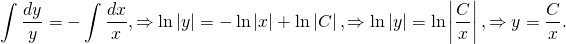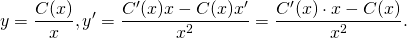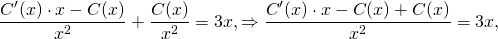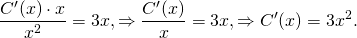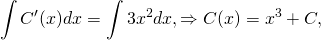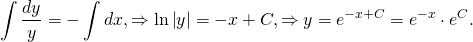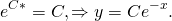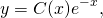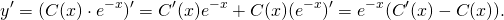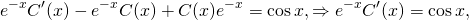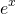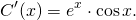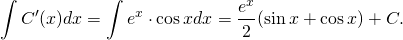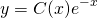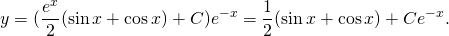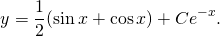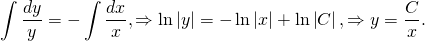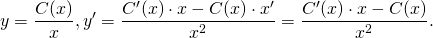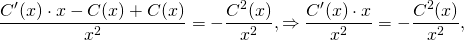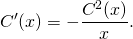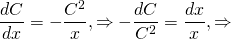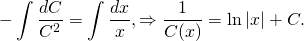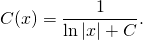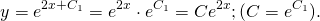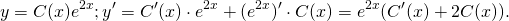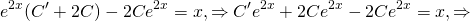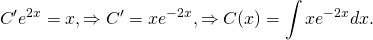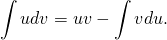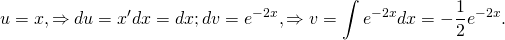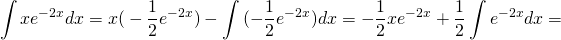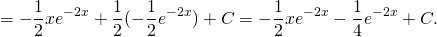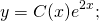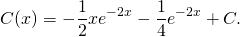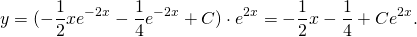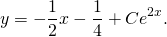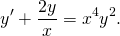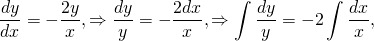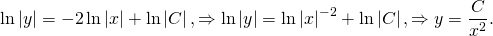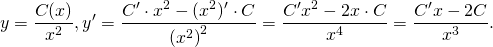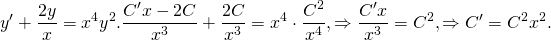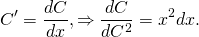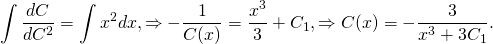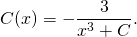Метод лагранжа вариации произвольных постоянных для уравнения 2 го порядка

Здесь мы применим метод вариации постоянных Лагранжа для решения линейных неоднородных дифференциальных уравнений второго порядка. Подробное описание этого метода для решения уравнений произвольного порядка изложено на странице
Решение линейных неоднородных дифференциальных уравнений высших порядков методом Лагранжа >>> .

Видео:19. Метод вариации произвольных постоянных. Линейные неоднородные диф уравнения 2-го порядкаСкачать

Пример 1

Решить дифференциальное уравнение второго порядка с постоянными коэффициентами методом вариации постоянных Лагранжа:
(1)

Шаг 1. Решение однородного уравнения

Вначале мы решаем однородное дифференциальное уравнение:
(2)
Ищем решение в виде . Составляем характеристическое уравнение:

Это уравнение второго порядка.

Решаем квадратное уравнение:
.
Корни кратные: . Фундаментальная система решений уравнения (2) имеет вид:
(3) .
Отсюда получаем общее решение однородного уравнения (2):
(4) .

Шаг 2. Вариация постоянных – замена постоянных функциями

Варьируем постоянные C ₁ и C ₂ . То есть заменим в (4) постоянные и на функции:
.
Ищем решение исходного уравнения (1) в виде:
(5) .

Находим вторую производную:
.
Подставляем в исходное уравнение (1):
(1) ;

.
Поскольку и удовлетворяют однородному уравнению (2), то сумма членов в каждом столбце последних трех строк дает нуль и предыдущее уравнение приобретает вид:
(7) .
Здесь .

Вместе с уравнением (6) мы получаем систему уравнений для определения функций и :
(6) :
(7) .

Решение системы уравнений

Решаем систему уравнений (6-7). Выпишем выражения для функций и :
.
Находим их производные:
;
.

Решаем систему уравнений (6-7) методом Крамера. Вычисляем определитель матрицы системы:

.
По формулам Крамера находим:
;
.

Итак, мы нашли производные функций:
;
.
Интегрируем (см. Методы интегрирования корней). Делаем подстановку
; ; ; .

Общее решение исходного уравнения:

;
.

Видео:9. Метод вариации произвольной постоянной ( метод Лагранжа ). Линейные дифференциальные уравнения.Скачать

Пример 2

Решить дифференциальное уравнение методом вариации постоянных Лагранжа:
(8)

Шаг 1. Решение однородного уравнения

Решаем однородное дифференциальное уравнение:

(9)
Ищем решение в виде . Составляем характеристическое уравнение:

Это уравнение имеет комплексные корни:
.
Фундаментальная система решений, соответствующая этим корням, имеет вид:
(10) .
Общее решение однородного уравнения (9):
(11) .

Шаг 2. Вариация постоянных – замена постоянных функциями

Теперь варьируем постоянные C ₁ и C ₂ . То есть заменим в (11) постоянные на функции:
.
Ищем решение исходного уравнения (8) в виде:
(12) .

Далее ход решения получается таким же, как в примере 1. Мы приходим к следующей системе уравнений для определения функций и :
(13) :
(14) .
Здесь .

Решение системы уравнений

Решаем эту систему. Выпишем выражения функций и :
.
Из таблицы производных находим:
;
.

Решаем систему уравнений (13-14) методом Крамера. Определитель матрицы системы:

.
По формулам Крамера находим:
;
.

Первый интеграл немного сложней (см. Интегрирование тригонометрических рациональных функций). Делаем подстановку :

.
Поскольку , то знак модуля под знаком логарифма можно опустить. Умножим числитель и знаменатель на :
.
Тогда
.

Общее решение исходного уравнения:

.

Автор: Олег Одинцов . Опубликовано: 05-08-2013 Изменено: 19-06-2017

Видео:10. ДУ. ЛНДУ 2 порядка. Метод вариации произвольных постоянных (2230 Минорский)Скачать

Метод вариации произвольной постоянной решения линейных неоднородных уравнений

Пример №1 . Найдём общее решение уравнения y» + 4y’ + 3y = 9e -3 x . Рассмотрим соответствующее однородное уравнение y» + 4y’ + 3y = 0. Корни его характеристического уравнения r 2 + 4r + 3 = 0 равны -1 и -3. Поэтому фундаментальная система решений однородного уравнения состоит из функций y₁ = e — x и y₂ = e -3 x . Решение неоднородного уравнения ищем в виде y = C₁(x)e — x + C₂(x)e -3 x . Для нахождения производных C’₁, C’₂ составляем систему уравнений (8)
C′₁·e -x +C′₂·e -3x =0
-C′₁·e -x -3C′₂·e -3x =9e -3x
решая которую, находим , Интегрируя полученные функции, имеем
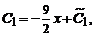
Окончательно получим

Пример №2 . Решить линейные дифференциальные уравнения второго порядка с постоянными коэффициентами методом вариации произвольных постоянных:

y(0) =1 + 3ln3
y’(0) = 10ln3

Решение:
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Решение уравнения будем искать в виде y = e rx . Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:
r 2 -6 r + 8 = 0
D = (-6) 2 — 4·1·8 = 4

Корни характеристического уравнения: r₁ = 4, r₂ = 2
Следовательно, фундаментальную систему решений составляют функции: y₁=e 4x , y₂=e 2x
Общее решение однородного уравнения имеет вид: y =C₁·e 4x +C₂·e 2x
Поиск частного решения методом вариации произвольной постоянной.
Для нахождения производных C’_i составляем систему уравнений:
C′₁·e 4x +C′₂·e 2x =0
C′₁(4e 4x ) + C′₂(2e 2x ) = 4/(2+e -2x )
Выразим C’₁ из первого уравнения:
C’₁ = -c₂e -2x
и подставим во второе. В итоге получаем:
C’₁ = 2/(e 2x +2e 4x )
C’₂ = -2e 2x /(e 2x +2e 4x )
Интегрируем полученные функции C’_i:
C₁ = 2ln(e -2x +2) — e -2x + C * ₁
C₂ = ln(2e 2x +1) – 2x+ C * ₂

Поскольку y =C₁·e 4x +C₂·e 2x , то записываем полученные выражения в виде:
C₁ = (2ln(e -2x +2) — e -2x + C * ₁) e 4x = 2 e 4x ln(e -2x +2) — e 2x + C * ₁ e 4x
C₂ = (ln(2e 2x +1) – 2x+ C * ₂)e 2x = e 2x ln(2e 2x +1) – 2x e 2x + C * ₂ e 2x
Таким образом, общее решение дифференциального уравнения имеет вид:
y = 2 e 4x ln(e -2x +2) — e 2x + C * ₁ e 4x + e 2x ln(2e 2x +1) – 2x e 2x + C * ₂ e 2x
или
y = 2 e 4x ln(e -2x +2) — e 2x + e 2x ln(2e 2x +1) – 2x e 2x + C * ₁ e 4x + C * ₂ e 2x

Найдем частное решение при условии:
y(0) =1 + 3ln3
y’(0) = 10ln3

Подставляя x = 0, в найденное уравнение, получим:
y(0) = 2 ln(3) — 1 + ln(3) + C * ₁ + C * ₂ = 3 ln(3) — 1 + C * ₁ + C * ₂ = 1 + 3ln3
Находим первую производную от полученного общего решения:
y’ = 2e 2x (2C₁ e 2x + C₂ -2x +4 e 2x ln(e -2x +2)+ ln(2e 2x +1)-2)
Подставляя x = 0, получим:
y’(0) = 2(2C₁ + C₂ +4 ln(3)+ ln(3)-2) = 4C₁ + 2C₂ +10 ln(3) -4 = 10ln3

Получаем систему из двух уравнений:
3 ln(3) — 1 + C * ₁ + C * ₂ = 1 + 3ln3
4C₁ + 2C₂ +10 ln(3) -4 = 10ln3
или
C * ₁ + C * ₂ = 2
4C₁ + 2C₂ = 4
или
C * ₁ + C * ₂ = 2
2C₁ + C₂ = 2
Откуда: C₁ = 0, C * ₂ = 2
Частное решение запишется как:
y = 2e 4x ·ln(e -2x +2) — e 2x + e 2x ·ln(2e 2x +1) – 2x·e 2x + 2·e 2x

Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Примеры на метод вариации произвольной постоянной

Метод вариации произвольной постоянной, или метод Лагранжа — еще один способ решения линейных дифференциальных уравнений первого порядка и уравнения Бернулли.

Линейные дифференциальные уравнения первого порядка — это уравнения вида y’+p(x)y=q(x). Если в правой части стоит нуль: y’+p(x)y=0, то это — линейное однородное уравнение 1го порядка. Соответственно, уравнение с ненулевой правой частью, y’+p(x)y=q(x), — неоднородное линейное уравнение 1го порядка.

Метод вариации произвольной постоянной (метод Лагранжа) состоит в следующем:

1) Ищем общее решение однородного уравнения y’+p(x)y=0: y=y*.

2) В общем решении С считаем не константой, а функцией от икса: С=С(x). Находим производную общего решения (y*)’ и в первоначальное условие подставляем полученное выражение для y* и (y*)’. Из полученного уравнения находим функцию С(x).

3) В общее решение однородного уравнения вместо С подставляем найденное выражение С(x).

Рассмотрим примеры на метод вариации произвольной постоянной. Возьмем те же задания, что и в примерах решения линейных дифференциальных уравнений методом Бернулли , сравним ход решения и убедимся, что полученные ответы совпадают.

1) y’=3x-y/x

Перепишем уравнение в стандартном виде (в отличие от метода Бернулли, где форма записи нам нужна была только для того, чтобы увидеть, что уравнение — линейное).

y’+y/x=3x (I). Теперь действуем по плану.

1) Решаем однородное уравнение y’+y/x=0. Это уравнение с разделяющимися переменными. Представляем y’=dy/dx, подставляем: dy/dx+y/x=0, dy/dx=-y/x. Обе части уравнения умножаем на dx и делим на xy≠0: dy/y=-dx/x. Интегрируем:

2) В полученном общем решении однородного уравнения будем считать С не константой, а функцией от x: С=С(x). Отсюда

Полученные выражения подставляем в условие (I):

Интегрируем обе части уравнения:

здесь С — уже некоторая новая константа.

3) В общее решение однородного уравнения y=C/x, где мы считали С=С(x), то есть y=C(x)/x, вместо С(x) подставляем найденное выражение x³+C: y=(x³+C)/x или y=x²+C/x. Получили такой же ответ, как и при решении методом Бернулли.

2) y’+y=cosx.

Здесь уравнение уже записано в стандартном виде, преобразовывать не надо.

1) Решаем однородное линейное уравнение y’+y=0: dy/dx=-y; dy/y=-dx. Интегрируем:

Чтобы получить более удобную форму записи, экспоненту в степени С примем за новую С:

Это преобразование выполнили, чтобы удобнее было находить производную.

2) В полученном общем решении линейного однородного уравнения считаем С не константой, а функцией от x: С=С(x). При этом условии

Полученные выражения y и y’ подставляем в условие:

Умножим обе части уравнения на

Интегрируем обе части уравнения по формуле интегрирования по частям, получаем:

Здесь С уже не функция, а обычная константа.

3) В общее решение однородного уравнения

подставляем найденную функцию С(x):

Получили такой же ответ, как и при решении методом Бернулли.

Метод вариации произвольной постоянной применим и для решения уравнений Бернулли .

y’x+y=-xy².

Приводим уравнение к стандартному виду: y’+y/x=-y² (II).

1) Решаем однородное уравнение y’+y/x=0. dy/dx=-y/x. Умножаем обе части уравнения на dx и делим на y: dy/y=-dx/x. Теперь интегрируем:

2) В полученном общем решении будем считать С не константой, а некоторой функций от x. При этом условии

Подставляем полученные выражения в условие (II):

Получили уравнение с разделяющимися переменными относительно С и x:

Здесь С — уже обычная константа. В процессе интегрирования писали вместо С(x) просто С, чтобы не перегружать запись. А в конце вернулись к С(x), чтобы не путать С(x) с новой С.

3) В общее решение однородного уравнения y=C(x)/x подставляем найденную функцию С(x):

Получили такой же ответ, что и при решении способом Бернулли.

Примеры для самопроверки:

1) Решаем однородное уравнение y’-2y=0. y’=dy/dx, отсюда dy/dx=2y, умножаем обе части уравнения на dx, делим на y и интегрируем:

Отсюда находим y:

2) В полученном решении С будем считать не константой, а функцией от x: C=C(x). Тогда

Выражения для y и y’ подставляем в условие (для краткости будем питать С вместо С(x) и С’ вместо C'(x)):

Для нахождения интеграла в правой части применяем формулу интегрирования по частям:

Теперь подставляем u, du и v в формулу:

3) Теперь подставляем в решение однородного

Отсюда получаем решение неоднородного уравнения:

2. Поделив обе части данного уравнения на x, приходим к уравнению

Это — уравнение Бернулли.

1) Решаем однородное уравнение y’+2y/x=0,

2) В этом решении заменяем константу С на функцию от x С(x), тогда

(для удобства пишем вместо С(x) просто С, но помним, что С здесь — функция от x). Теперь подставляем выражения для y и y’ в условие:

Интегрируем обе части уравнения:

Если ввести обозначение 3С1=С, то получим

3) В условие y=C(x)/x² подставляем найденное С(x):

💡 Видео

Математика без Ху!ни. Линейное неоднородное уравнение 1 порядка. Метод вариации постоянной.Скачать

16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать

Видеоурок "Метод вариации произвольных постоянных"Скачать

Метод вариаций произвольных постоянных (метод Лагранжа) для линейных дифф. уравнений 2-го порядкаСкачать

Метод вариации произвольных постоянных ЛагранжаСкачать

Метод вариации постоянных ПрактикаСкачать

Линейное однородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами.Скачать

Метод вариации произвольных постоянных.Скачать

ЛОДУ 2 порядка c постоянными коэффициентамиСкачать

Метод вариации постоянных ТеорияСкачать

Лекция №15 по ДУ. Метод вариации постоянных для уравнений n-го порядка. Бишаев А.МСкачать

Метод вариации произвольной переменнойСкачать

ЛНДУ. Метод вариации произвольных постоянных.Скачать

Метод Лагранжа & Метод Бернулли ★ Решение линейных неоднородных дифференциальных уравненийСкачать

Метод Бернулли. Метод Лагранжа (вариации произвольной постоянной). Линейное дифуравнение 1 порядкаСкачать