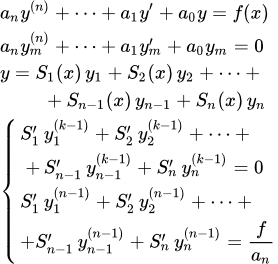Метод лагранжа решения неоднородного линейного уравнения

Видео:Метод Лагранжа & Метод Бернулли ★ Решение линейных неоднородных дифференциальных уравненийСкачать

Метод Лагранжа (вариация постоянных)

Рассмотрим линейное неоднородное дифференциальное уравнение с постоянными коэффициентами произвольного n-го порядка:
(1) .
Метод вариации постоянной, рассмотренный нами для уравнения первого порядка, также применим и для уравнений более высоких порядков.

Решение выполняется в два этапа. На первом этапе мы отбрасываем правую часть и решаем однородное уравнение. В результате получаем решение, содержащее n произвольных постоянных. На втором этапе мы варьируем постоянные. То есть мы считаем, что эти постоянные являются функциями от независимой переменной x и находим вид этих функций.

Хотя мы здесь рассматриваем уравнения с постоянными коэффициентами, но метод Лагранжа также применим и для решения любых линейных неоднородных уравнений. Для этого, однако, должна быть известна фундаментальная система решений однородного уравнения.

Шаг 1. Решение однородного уравнения

Как и в случае уравнений первого порядка, вначале мы ищем общее решение однородного уравнения, приравнивая правую неоднородную часть к нулю:
(2) .
Общее решение такого уравнения имеет вид:
(3) .
Здесь – произвольные постоянные; – n линейно независимых решений однородного уравнения (2), которые образуют фундаментальную систему решений этого уравнения.

Шаг 2. Вариация постоянных – замена постоянных функциями

На втором этапе мы займемся вариацией постоянных. Другими словами, мы заменим постоянные на функции от независимой переменной x :
.
То есть мы ищем решение исходного уравнения (1) в следующем виде:
(4) .

Если мы подставим (4) в (1), то получим одно дифференциальное уравнение для n функций . При этом мы можем связать эти функции дополнительными уравнениями. Тогда получится n уравнений, из которых можно определить n функций . Дополнительные уравнения можно составить различными способами. Но мы это сделаем так, чтобы решение имело наиболее простой вид. Для этого, при дифференцировании, нужно приравнивать к нулю члены, содержащие производные от функций . Продемонстрируем это.

Чтобы подставить предполагаемое решение (4) в исходное уравнение (1), нам нужно найти производные первых n порядков от функции, записанной в виде (4). Дифференцируем (4), применяя правила дифференцирования суммы и произведения:
.
Сгруппируем члены. Сначала выпишем члены с производными от , а затем – члены с производными от :

.
Наложим на функции первое условие:
(5.1) .
Тогда выражение для первой производной по будет иметь более простой вид:
(6.1) .

Тем же способом находим вторую производную:

.
Наложим на функции второе условие:
(5.2) .
Тогда
(6.2) .
И так далее. В дополнительных условиях, мы приравниваем члены, содержащие производные функций , к нулю.

Таким образом, если выбрать следующие дополнительные уравнения для функций :
(5.k) ,
то первые производных по будут иметь наиболее простой вид:
(6.k) .
Здесь .

Подставляем в исходное уравнение (1):
(1) ;

.
Учтем, что все функции удовлетворяют уравнению (2):
.
Тогда сумма членов, содержащих дают нуль. В итоге получаем:
(7) .

В результате мы получили систему линейных уравнений для производных :
(5.1) ;
(5.2) ;
(5.3) ;
. . . . . . .
(5.n-1) ;
(7′) .

Решая эту систему, находим выражения для производных как функции от x . Интегрируя, получим:
.
Здесь – уже не зависящие от x постоянные. Подставляя в (4), получаем общее решение исходного уравнения.

Заметим, что для определения величин производных мы нигде не использовали тот факт, что коэффициенты a_i являются постоянными. Поэтому метод Лагранжа применим для решения любых линейных неоднородных уравнений, если известна фундаментальная система решений однородного уравнения (2).

Далее рассмотрены примеры решения уравнений методом Лагранжа.

Видео:9. Метод вариации произвольной постоянной ( метод Лагранжа ). Линейные дифференциальные уравнения.Скачать

Примеры

Решить уравнения методом вариации постоянных (Лагранжа).

Решение примеров > > >

Автор: Олег Одинцов . Опубликовано: 05-08-2013 Изменено: 22-06-2017

Видео:19. Метод вариации произвольных постоянных. Линейные неоднородные диф уравнения 2-го порядкаСкачать

Метод вариации произвольной постоянной решения линейных неоднородных уравнений

Пример №1 . Найдём общее решение уравнения y» + 4y’ + 3y = 9e -3 x . Рассмотрим соответствующее однородное уравнение y» + 4y’ + 3y = 0. Корни его характеристического уравнения r 2 + 4r + 3 = 0 равны -1 и -3. Поэтому фундаментальная система решений однородного уравнения состоит из функций y₁ = e — x и y₂ = e -3 x . Решение неоднородного уравнения ищем в виде y = C₁(x)e — x + C₂(x)e -3 x . Для нахождения производных C’₁, C’₂ составляем систему уравнений (8)
C′₁·e -x +C′₂·e -3x =0
-C′₁·e -x -3C′₂·e -3x =9e -3x
решая которую, находим , Интегрируя полученные функции, имеем
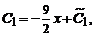
Окончательно получим

Пример №2 . Решить линейные дифференциальные уравнения второго порядка с постоянными коэффициентами методом вариации произвольных постоянных:

y(0) =1 + 3ln3
y’(0) = 10ln3

Решение:
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Решение уравнения будем искать в виде y = e rx . Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:
r 2 -6 r + 8 = 0
D = (-6) 2 — 4·1·8 = 4

Корни характеристического уравнения: r₁ = 4, r₂ = 2
Следовательно, фундаментальную систему решений составляют функции: y₁=e 4x , y₂=e 2x
Общее решение однородного уравнения имеет вид: y =C₁·e 4x +C₂·e 2x
Поиск частного решения методом вариации произвольной постоянной.
Для нахождения производных C’_i составляем систему уравнений:
C′₁·e 4x +C′₂·e 2x =0
C′₁(4e 4x ) + C′₂(2e 2x ) = 4/(2+e -2x )
Выразим C’₁ из первого уравнения:
C’₁ = -c₂e -2x
и подставим во второе. В итоге получаем:
C’₁ = 2/(e 2x +2e 4x )
C’₂ = -2e 2x /(e 2x +2e 4x )
Интегрируем полученные функции C’_i:
C₁ = 2ln(e -2x +2) — e -2x + C * ₁
C₂ = ln(2e 2x +1) – 2x+ C * ₂

Поскольку y =C₁·e 4x +C₂·e 2x , то записываем полученные выражения в виде:
C₁ = (2ln(e -2x +2) — e -2x + C * ₁) e 4x = 2 e 4x ln(e -2x +2) — e 2x + C * ₁ e 4x
C₂ = (ln(2e 2x +1) – 2x+ C * ₂)e 2x = e 2x ln(2e 2x +1) – 2x e 2x + C * ₂ e 2x
Таким образом, общее решение дифференциального уравнения имеет вид:
y = 2 e 4x ln(e -2x +2) — e 2x + C * ₁ e 4x + e 2x ln(2e 2x +1) – 2x e 2x + C * ₂ e 2x
или
y = 2 e 4x ln(e -2x +2) — e 2x + e 2x ln(2e 2x +1) – 2x e 2x + C * ₁ e 4x + C * ₂ e 2x

Найдем частное решение при условии:
y(0) =1 + 3ln3
y’(0) = 10ln3

Подставляя x = 0, в найденное уравнение, получим:
y(0) = 2 ln(3) — 1 + ln(3) + C * ₁ + C * ₂ = 3 ln(3) — 1 + C * ₁ + C * ₂ = 1 + 3ln3
Находим первую производную от полученного общего решения:
y’ = 2e 2x (2C₁ e 2x + C₂ -2x +4 e 2x ln(e -2x +2)+ ln(2e 2x +1)-2)
Подставляя x = 0, получим:
y’(0) = 2(2C₁ + C₂ +4 ln(3)+ ln(3)-2) = 4C₁ + 2C₂ +10 ln(3) -4 = 10ln3

Получаем систему из двух уравнений:
3 ln(3) — 1 + C * ₁ + C * ₂ = 1 + 3ln3
4C₁ + 2C₂ +10 ln(3) -4 = 10ln3
или
C * ₁ + C * ₂ = 2
4C₁ + 2C₂ = 4
или
C * ₁ + C * ₂ = 2
2C₁ + C₂ = 2
Откуда: C₁ = 0, C * ₂ = 2
Частное решение запишется как:
y = 2e 4x ·ln(e -2x +2) — e 2x + e 2x ·ln(2e 2x +1) – 2x·e 2x + 2·e 2x

Видео:7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать

Линейные неоднородные дифференциальные уравнения первого порядка

В данной теме поговорим о способах решения линейных неоднородных дифференциальных уравнений вида y ‘ = P ( x ) · y = Q ( x ) . Начнем с метода вариации произвольной постоянной и покажем способ применения этого метода для решения задачи Коши. Продолжим рассмотрением метода, который предполагает представление произвольной постоянной у как произведения двух функций u ( x ) и v ( x ) . В разделе мы приводим большое количество задач по теме с детальным разбором решения.

На тот случай, если применяемые при разборе темы термины и понятия окажутся незнакомыми для вас, мы рекомендуем заглядывать в раздел «Основные термины и определения теории дифференциальных уравнений».

Видео:16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать

Метод вариации произвольной постоянной для решения ЛНДУ первого порядка

Для краткости будет обозначать линейное неоднородное дифференциальное уравнение аббревиатурой ЛНДУ, а линейное однородное дифференциальное уравнение (ЛОДУ).

ЛНДУ вида y ‘ = P ( x ) · y = Q ( x ) соответствует ЛОДУ вида y ‘ = P ( x ) · y = 0 , при Q ( x ) = 0 . Если посмотреть на дифференциальное уравнение y ‘ = P ( x ) · y = 0 , становится понятно, что мы имеем дело с уравнением с разделяющимися переменными. Мы можем его проинтегрировать: y ‘ = P ( x ) · y = 0 ⇔ d y y = — P ( x ) d x , y ≠ 0 ∫ d y y = — ∫ P ( x ) d x ⇔ ln y + C 1 = — ∫ P ( x ) d x ⇔ ln y = ln C — ∫ P ( x ) d x , ln C = — C 1 , C ≠ 0 ⇔ e ln y = e ln C — ∫ P ( x ) d x ⇔ y = C · e — ∫ P ( x ) d x

Мы можем утверждать, что значение переменной y = 0 тоже является решением, так как при этом значении переменной уравнение y ‘ = P ( x ) · y = 0 обращается в тождество. Этому случаю соответствует решение y = C · e — ∫ P ( x ) d x при значении C = 0 .

Получается, что y = C · e — ∫ P ( x ) d x — общее решение ЛОДУ, где С – произвольная постоянная.

y = C · e — ∫ P ( x ) d x — это решение ЛОДУ y ‘ = P ( x ) · y = 0 .

Для того, чтобы найти общее решение неоднородного уравнения y ‘ = P ( x ) · y = Q ( x ) , будем считать С не константой, а функцией аргумента х . Фактически, мы примем y = C ( x ) · e — ∫ P ( x ) d x общим решением ЛНДУ.

Подставим y = C ( x ) · e — ∫ P ( x ) d x в дифференциальное уравнение y ‘ = P ( x ) · y = Q ( x ) . Оно при этом обращается в тождество:

y ‘ = P ( x ) · y = Q ( x ) C x · e — ∫ P ( x ) d x + P ( x ) · C ( x ) · e — ∫ P ( x ) d x = Q ( x )

Теперь обратимся к правилу дифференцирования произведения. Получаем:

C ‘ ( x ) · e — ∫ P ( x ) d x + C ( x ) · e — ∫ P ( x ) d x + P ( x ) · C ( x ) · e — ∫ P ( x ) d x = Q ( x )

Производная сложной функции e — ∫ P ( x ) d x ‘ равна e — ∫ P ( x ) d x · — ∫ P ( x ) d x ‘ .

Теперь вспомним свойства неопределенного интеграла. Получаем:

e — ∫ P ( x ) d x · — ∫ P ( x ) d x ‘ = — e — ∫ P ( x ) d x · P ( x )

Теперь выполним переход:

C ‘ ( x ) · e — ∫ P ( x ) d x + C ( x ) · e — ∫ P ( x ) d x ‘ + P ( x ) · C ( x ) · e — ∫ P ( x ) d x = Q ( x ) C ‘ ( x ) · e — ∫ P ( x ) d x — P ( x ) · C ( x ) · e — ∫ P ( x ) d x + P ( x ) · C ( x ) · e — ∫ P ( x ) d x = Q ( x ) C ‘ ( x ) · e — ∫ P ( x ) d x = Q ( x )

Так мы пришли к простейшему дифференциальному уравнению первого порядка. В ходе решения этого уравнения мы определим функцию C ( x ) . Это позволит нам записать решение исходного ЛНДУ первого порядка следующим образом:

y = C ( x ) · e — ∫ P ( x ) d x

Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Подведем итог

Метод вариации произвольной постоянной при решении ЛНДУ предполагает проведение трех этапов:

• нахождение общего решения соответствующего ЛОДУ y ‘ + P ( x ) · y = 0 в виде y = C · e — ∫ P ( x ) d x ;
• варьирование произвольной постоянной С , что заключается в замене ее функцией С ( x ) ;
• подстановка функции y = C ( x ) · e — ∫ P ( x ) d x в исходное дифференциальное уравнение, откуда мы можем вычислить C ( x ) и записать ответ.

Теперь применим этот алгоритм к решению задачи.

Найдите решение задачи Коши y ‘ — 2 x y 1 + x 2 = 1 + x 2 , y ( 1 ) = 3 .

Нам нужно отыскать частное решение ЛНДУ y ‘ — 2 x y 1 + x 2 = 1 + x 2 при начальном условии y ( 1 ) = 3 .

В нашем примере P ( x ) = — 2 x 1 + x 2 и Q ( x ) = x 2 + 1 . Начнем с того, что найдем общее решение ЛОДУ. После этого применим метод вариации произвольной постоянной и определим общее решение ЛНДУ. Это позволит нам найти искомое частное решение.

Общим решением соответствующего ЛОДУ y ‘ — 2 x y 1 + x 2 = 0 будет семейство функций y = C · ( x 2 + 1 ) , где С – произвольная постоянная.

Варьируем произвольную постоянную y = C ( x ) · ( x 2 + 1 ) и подставляем эту функцию в исходное уравнение:
y ‘ — 2 x y 1 + x 2 = 1 + x 2 C x · ( x 2 + 1 ‘ — 2 x · C ( x ) · ( x 2 + 1 ) 1 + x 2 = 1 + x 2 C ‘ ( x ) · ( x 2 + 1 ) + C ( x ) · 2 x — 2 x · C ( x ) = 1 + x 2 C ‘ ( x ) = 1 ,

откуда C ( x ) = ∫ d x = x + C 1 , где C 1 – произвольная постоянная.

Это значит, что y = C ( x ) · ( x 2 + 1 ) = ( x + C 1 ) · ( x 2 + 1 ) — общее решение неоднородного уравнения.

Теперь приступим к отысканию частного решения, которое будет удовлетворять начальному условию y ( 1 ) = 3 .

Так как y = ( x + C 1 ) · ( x 2 + 1 ) , то y ( 1 ) = ( 1 + C 1 ) · ( 1 2 + 1 ) = 2 · ( 1 + C 1 ) . Обратившись к начальному условию, получаем уравнение 2 · ( 1 + C 1 ) = 3 , откуда C 1 = 1 2 . Следовательно, искомое решение задачи Коши имеет вид y = x + 1 2 · ( x 2 + 1 )

Теперь рассмотрим еще один метод решения линейных неоднородных дифференциальных уравнений y ‘ + P ( x ) · y = Q ( x ) .

Видео:Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами 4y''-y=x^3-24x #1Скачать

Еще один метод решения ЛНДУ первого порядка

Мы можем представить неизвестную функцию как произведение y = u ⋅ v , где u и v – функции аргумента x .

Мы можем подставить эту функцию в ЛНДУ первого порядка. Имеем:

y ‘ + P ( x ) · y = Q ( x ) ( u · v ) ‘ + P ( x ) · u · v = Q ( x ) u ‘ · v + u · v ‘ + P ( x ) · u · v = Q ( x ) u ‘ · v + u · ( v ‘ + P ( x ) · v ) = Q ( x )

Если найти такое v , чтобы оно было ненулевым частным решением дифференциального уравнения v ‘ + P ( x ) · v = 0 , то u можно будет определить из уравнения с разделяющимися переменными u ‘ · v = Q ( x ) .

Рассмотрим этот алгоритм решения на предыдущем примере. Это позволит нам сосредоточиться на главном, не отвлекаясь на второстепенные детали.

Найдите общее решение линейного неоднородного дифференциального уравнения y ‘ — 2 x y 1 + x 2 = 1 + x 2 .

Пусть y = u ⋅ v , тогда
y ‘ — 2 x y x 2 + 1 = x 2 + 1 ⇔ ( u · v ) — 2 x · u · v x 2 + 1 = x 2 + 1 u ‘ · v + u · v ‘ — 2 x · u · v x 2 + 1 = x 2 + 1 u ‘ · v + u · v ‘ — 2 x · v x 2 + 1 = x 2 + 1

Находим такое v , отличное от нуля, чтобы выражение в скобках обращалось в ноль. Иными словами, находим частное решение дифференциального уравнения v ‘ — 2 x · v x 2 + 1 = 0 .
v ‘ — 2 x · v x 2 + 1 = 0 ⇔ d v d x = 2 x · v x 2 + 1 ⇒ d v v = 2 x d x x 2 + 1 ⇔ d v v = d ( x 2 + 1 ) x 2 + 1 ∫ d v v = ∫ d ( x 2 + 1 ) x 2 + 1 ln v + C 1 = ln ( x 2 + 1 ) + C 2

Возьмем частное решение v = x 2 + 1 , соответствующее C 2 – С 1 = 0 .

Для этого частного решения имеем
u ‘ · v + u · v ‘ — 2 x · v x 2 + 1 = x 2 + 1 ⇔ u ‘ · ( x 2 + 1 ) + u · 0 = x 2 + 1 ⇔ u ‘ = 1 ⇔ u = x + C

Следовательно, общее решение исходного линейного неоднородного дифференциального уравнения есть y = u · v = ( x + C ) · ( x 2 + 1 )

Ответы в обоих случаях совпадают. Это значит, что оба метода решения, которые мы привели в статье, равнозначны. Выбирать, какой из них применить для решения задачи, вам.

📽️ Видео

Математика без Ху!ни. Линейное неоднородное уравнение 1 порядка. Метод вариации постоянной.Скачать

Дифференциальные уравнения. Метод Лагранжа. Метод вариации произвольной постоянной.Скачать

Линейные неоднородные дифференциальные уравнения 1-го порядка. Метод Лагранжа. (ч. 2).Скачать

Метод Бернулли. Метод ЛагранжаСкачать

Линейные неоднородные дифференциальные уравнения 1-го порядка. Метод Лагранжа. (ч.1)Скачать

Видеоурок "Метод вариации произвольных постоянных"Скачать

Линейное дифференциальное уравнение первого порядка (1-x^2)*y'-xy=1Скачать

20. Методы решения линейных неоднородных уравненийСкачать

ЛНДУ I порядка. Метод ЛагранжаСкачать

Неоднородная система линейных уравненийСкачать

10. ДУ. ЛНДУ 2 порядка. Метод вариации произвольных постоянных (2230 Минорский)Скачать

Метод Лагранжа. Решение линейного дифференциального уравнения первого порядка.Скачать