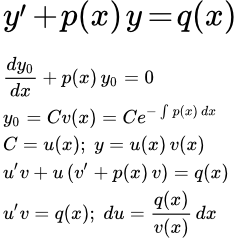Метод лагранжа для решения систем дифференциальных уравнений (3 видео)

Метод Лагранжа (вариации постоянной). Линейные дифференциальные уравнения первого порядка.

Рассмотрим линейное неоднородное дифференциальное уравнение первого порядка:
(1) .
Существует три способа решения этого уравнения:

Рассмотрим решение линейного дифференциального уравнения первого порядка методом Лагранжа.

Содержание

Метод вариации постоянной (Лагранжа)
Шаг 1 Решение однородного уравнения
Шаг 2 Заменим постоянную C на функцию
Пример решения линейного дифференциального уравнения первого порядка методом Лагранжа
Метод вариации произвольной постоянной решения линейных неоднородных уравнений
Уравнение Лагранжа
Общий метод решения уравнения Лагранжа
Решение типичных задач
Готовые работы на аналогичную тему
💡 Видео

Видео:9. Метод вариации произвольной постоянной ( метод Лагранжа ). Линейные дифференциальные уравнения.Скачать

Метод вариации постоянной (Лагранжа)

В методе вариации постоянной мы решаем уравнение в два этапа. На первом этапе мы упрощаем исходное уравнение и решаем однородное уравнение. На втором этапе мы заменим постоянную интегрирования, полученную на первой стадии решения, на функцию. После чего ищем общее решение исходного уравнения.

Шаг 1 Решение однородного уравнения

Ищем решение однородного уравнения:

Это уравнение с разделяющимися переменными

Разделяем переменные — умножаем на dx , делим на y :

Интегрируем:

Интеграл по y — табличный:

Тогда

Потенцируем:

Заменим постоянную e C на C и уберем знак модуля, что сводится к умножению на постоянную ±1 , которую включим в C :

Шаг 2 Заменим постоянную C на функцию

Теперь заменим постоянную C на функцию от x :
C → u ( x )
То есть, будем искать решение исходного уравнения (1) в виде:
(2)
Находим производную.

По правилу дифференцирования сложной функции:
.
По правилу дифференцирования произведения:

.
Подставляем в исходное уравнение (1):
(1) ;

.
Два члена сокращаются:
;
.
Интегрируем:
.
Подставляем в (2):
.
В результате получаем общее решение линейного дифференциального уравнения первого порядка:
.

Видео:Видеоурок "Системы дифференциальных уравнений"Скачать

Пример решения линейного дифференциального уравнения первого порядка методом Лагранжа

Решаем однородное уравнение:

Разделяем переменные:

Умножим на :

Интегрируем:

Интегралы табличные:

Потенцируем:

Заменим постоянную e C на C и убираем знаки модуля:

Отсюда:

Заменим постоянную C на функцию от x :
C → u ( x )

Находим производную:
.
Подставляем в исходное уравнение:
;
;
Или:
;
.
Интегрируем:
;
Решение уравнения:
.

Общее решение уравнения:
.

Автор: Олег Одинцов . Опубликовано: 27-07-2012 Изменено: 01-03-2015

Видео:Решение системы дифференциальных уравнений методом ЭйлераСкачать

Метод вариации произвольной постоянной решения линейных неоднородных уравнений

Пример №1 . Найдём общее решение уравнения y» + 4y’ + 3y = 9e -3 x . Рассмотрим соответствующее однородное уравнение y» + 4y’ + 3y = 0. Корни его характеристического уравнения r 2 + 4r + 3 = 0 равны -1 и -3. Поэтому фундаментальная система решений однородного уравнения состоит из функций y₁ = e — x и y₂ = e -3 x . Решение неоднородного уравнения ищем в виде y = C₁(x)e — x + C₂(x)e -3 x . Для нахождения производных C’₁, C’₂ составляем систему уравнений (8)
C′₁·e -x +C′₂·e -3x =0
-C′₁·e -x -3C′₂·e -3x =9e -3x
решая которую, находим , Интегрируя полученные функции, имеем
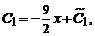
Окончательно получим

Пример №2 . Решить линейные дифференциальные уравнения второго порядка с постоянными коэффициентами методом вариации произвольных постоянных:

y(0) =1 + 3ln3
y’(0) = 10ln3

Решение:
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Решение уравнения будем искать в виде y = e rx . Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:
r 2 -6 r + 8 = 0
D = (-6) 2 — 4·1·8 = 4

Корни характеристического уравнения: r₁ = 4, r₂ = 2
Следовательно, фундаментальную систему решений составляют функции: y₁=e 4x , y₂=e 2x
Общее решение однородного уравнения имеет вид: y =C₁·e 4x +C₂·e 2x
Поиск частного решения методом вариации произвольной постоянной.
Для нахождения производных C’_i составляем систему уравнений:
C′₁·e 4x +C′₂·e 2x =0
C′₁(4e 4x ) + C′₂(2e 2x ) = 4/(2+e -2x )
Выразим C’₁ из первого уравнения:
C’₁ = -c₂e -2x
и подставим во второе. В итоге получаем:
C’₁ = 2/(e 2x +2e 4x )
C’₂ = -2e 2x /(e 2x +2e 4x )
Интегрируем полученные функции C’_i:
C₁ = 2ln(e -2x +2) — e -2x + C * ₁
C₂ = ln(2e 2x +1) – 2x+ C * ₂

Поскольку y =C₁·e 4x +C₂·e 2x , то записываем полученные выражения в виде:
C₁ = (2ln(e -2x +2) — e -2x + C * ₁) e 4x = 2 e 4x ln(e -2x +2) — e 2x + C * ₁ e 4x
C₂ = (ln(2e 2x +1) – 2x+ C * ₂)e 2x = e 2x ln(2e 2x +1) – 2x e 2x + C * ₂ e 2x
Таким образом, общее решение дифференциального уравнения имеет вид:
y = 2 e 4x ln(e -2x +2) — e 2x + C * ₁ e 4x + e 2x ln(2e 2x +1) – 2x e 2x + C * ₂ e 2x
или
y = 2 e 4x ln(e -2x +2) — e 2x + e 2x ln(2e 2x +1) – 2x e 2x + C * ₁ e 4x + C * ₂ e 2x

Найдем частное решение при условии:
y(0) =1 + 3ln3
y’(0) = 10ln3

Подставляя x = 0, в найденное уравнение, получим:
y(0) = 2 ln(3) — 1 + ln(3) + C * ₁ + C * ₂ = 3 ln(3) — 1 + C * ₁ + C * ₂ = 1 + 3ln3
Находим первую производную от полученного общего решения:
y’ = 2e 2x (2C₁ e 2x + C₂ -2x +4 e 2x ln(e -2x +2)+ ln(2e 2x +1)-2)
Подставляя x = 0, получим:
y’(0) = 2(2C₁ + C₂ +4 ln(3)+ ln(3)-2) = 4C₁ + 2C₂ +10 ln(3) -4 = 10ln3

Получаем систему из двух уравнений:
3 ln(3) — 1 + C * ₁ + C * ₂ = 1 + 3ln3
4C₁ + 2C₂ +10 ln(3) -4 = 10ln3
или
C * ₁ + C * ₂ = 2
4C₁ + 2C₂ = 4
или
C * ₁ + C * ₂ = 2
2C₁ + C₂ = 2
Откуда: C₁ = 0, C * ₂ = 2
Частное решение запишется как:
y = 2e 4x ·ln(e -2x +2) — e 2x + e 2x ·ln(2e 2x +1) – 2x·e 2x + 2·e 2x

Видео:19. Метод вариации произвольных постоянных. Линейные неоднородные диф уравнения 2-го порядкаСкачать

Уравнение Лагранжа

Вы будете перенаправлены на Автор24

Видео:Дифференциальные уравнения. Метод Лагранжа. Метод вариации произвольной постоянной.Скачать

Общий метод решения уравнения Лагранжа

Предположим, что некоторое дифференциальное уравнение первого порядка $Fleft(x,y,y’right)=0$, не разрешенное относительно производной, удалось разрешить относительно $y$, то есть представить в виде $y=fleft(x,y’right)$.

Частным случаем дифференциального уравнения такого вида является уравнение Лагранжа $y=xcdot phi left(y’right)+psi left(y’right)$, в котором $phi left(y’right)ne y’$.

Дифференциальное уравнение Лагранжа решают методом введения параметра $y’=p$.

При этом исходное дифференциальное уравнение можно переписать в виде $y=xcdot phi left(pright)+psi left(pright)$.

Выполнив дифференцирование по $x$ с учетом $dy=pcdot dx$, после несложных алгебраических преобразований получаем линейное дифференциальное уравнение относительно функции $xleft(pright)$ и её производной $frac $, а именно: $frac -frac cdot x=frac $.

Это уравнение решается известным методом, в результате чего получим его общее решение $x=Fleft(p,Cright)$.

Подставив полученный результат в соотношение $y=xcdot phi left(pright)+psi left(pright)$, получим $y=Fleft(p,Cright)cdot phi left(pright)+psi left(pright)$.

Дополнительные частные либо особые решения уравнения Лагранжа могут быть получены в результате нахождения действительных корней уравнения $p-phi left(pright)=0$ и подстановки их в $y=xcdot phi left(pright)+psi left(pright)$.

Видео:Системы дифференциальных уравнений. Часть 2Скачать

Решение типичных задач

Решить дифференциальное уравнение $y=-xcdot y’+y’^ $.

Имеем дифференциальное уравнение Лагранжа, в котором $phi left(y’right)=-y’$ и $psi left(y’right)=y’^ $.

Вводим параметр $y’=p$ и получаем $y=-xcdot p+p^ $, а также $phi left(pright)=-p$ и $psi left(pright)=p^ $.

Теперь получим уравнение вида $frac -frac cdot x=frac $. Для этого находим: $phi ‘left(pright)=-1$; $psi ‘left(pright)=2cdot p$; $p-phi left(pright)=p-left(-pright)=2cdot p$.

Уравнение приобретает вид: $frac +frac cdot x=1$.

Применяем алгоритм решения линейного неоднородного дифференциального уравнения:

Стандартный вид $frac+fraccdot x=1$, где $Pleft(pright)=frac$, $Qleft(pright)=1$.
Вычисляем интеграл $I_ =int Pleft(pright)cdot dp =int fraccdot dp =fraccdot ln left|pright|$.

Выбираем для $vleft(pright)$ простейший ненулевой вариант: $vleft(pright)=frac <sqrt

> $.

Вычисляем интеграл $I_ =int fraccdot dp =int sqrt

cdot dp =fraccdot p^<frac> $ и получаем $uleft(p,Cright)=fraccdot p^<frac> +C$.

Получаем общее решение данного линейного неоднородного дифференциального уравнения в виде $x=left(fraccdot p^<frac> +Cright)cdot frac<sqrt

> =fraccdot p+frac<sqrt

> $.

Подставляем полученный результат в $y=xcdot phi left(pright)+psi left(pright)$. Получаем: $y=-left(frac cdot p+frac <sqrt

> right)cdot p+p^ =frac cdot p^ -Ccdot sqrt

Таким образом, общее решение данного уравнения Лагранжа в параметрической форме имеет вид: $left<begin <x=frac cdot p+frac <sqrt

> > \ <y=frac cdot p^ -Ccdot sqrt

> endright. $.

Для определения дополнительных частных либо особых решений находим корни уравнения $p-phi left(pright)=0$: получаем $p=0$.

Подставляем $p=0$ в $y=-xcdot p+p^ $ и получаем $y=0$. Это решение является частным, так как получается из общего при $C=frac cdot p^<frac > $.

Готовые работы на аналогичную тему

Решить дифференциальное уравнение $y=xcdot y’cdot left(y’+2right)$.

Имеем дифференциальное уравнение Лагранжа, в котором $phi left(y’right)=y’cdot left(y’+2right)$ и $psi left(y’right)=0$.

Вводим параметр $y’=p$ и получаем $y=xcdot pcdot left(p+2right)$, а также $phi left(pright)=pcdot left(p+2right)$ и $psi left(pright)=0$.

Теперь получим уравнение вида $frac -frac cdot x=frac $. Для этого находим: $phi ‘left(pright)=2cdot p+2$; $psi ‘left(pright)=0$; $p-phi left(pright)=p-left(p^ +2cdot pright)=-p^ -p$.

Уравнение приобретает вид:

Имеем стандартный вид $x’+Pleft(pright)cdot x=0$, где $Pleft(pright)=frac
$.
Вычисляем интеграл $I=int Pleft(pright)cdot dp =int frac
cdot dp =2cdot ln left|pright|$.
Записываем общее решение в виде $x=Ccdot e^ $ и выполняем упрощающие преобразования:

Подставляем полученный результат в $y=xcdot pcdot left(p+2right)$. Получаем: $y=frac <p^> cdot pcdot left(p+2right)$ или $y=Ccdot left(1+frac

right)$.

Таким образом, общее решение данного уравнения Лагранжа в параметрической форме имеет вид: $left<begin <x=frac <p^> > \ <y=Ccdot left(1+frac

right)> endright. $.

Параметр $p$ из этой системы можно исключить:

$p=frac <sqrt> <pm sqrt> $; $y=Ccdot left(1pm frac <2cdot sqrt> <sqrt> right)$ — это результат решения в явной форме.

Для определения дополнительных частных либо особых решений находим корни уравнения $p-phi left(pright)=-p^ -p=0$.

Получаем: $pcdot left(p+1right)=0$, откуда имеем два корня $p=0$ и $p=-1$.

Подставляем первый корень $p=0$ в $y=xcdot pcdot left(p+2right)$ и получаем первое дополнительное решение данного уравнения $y=0$. Это решение является частным, так как получается из общего при $C=0$.

Подставляем второй корень $p=-1$ в $y=xcdot pcdot left(p+2right)$ и получаем второе дополнительное решение данного уравнения $y=-x$. Это решение является особым, так как не получается из общего ни при каком $C$.