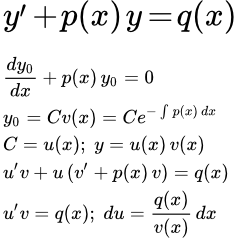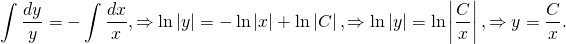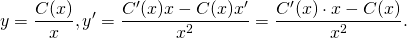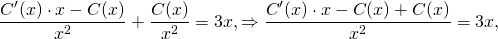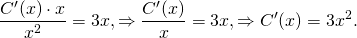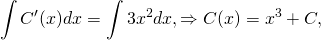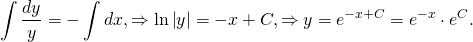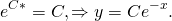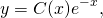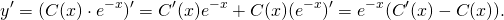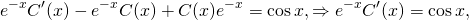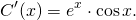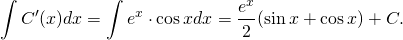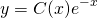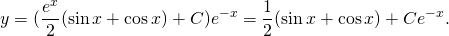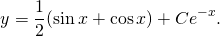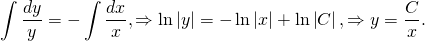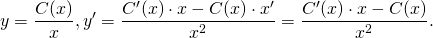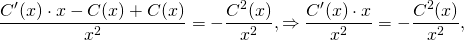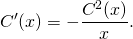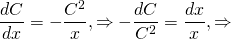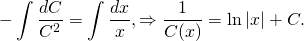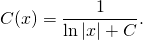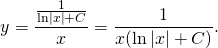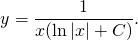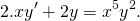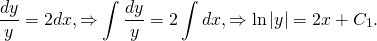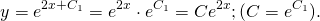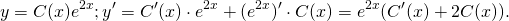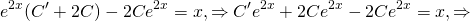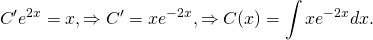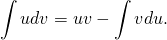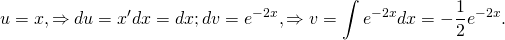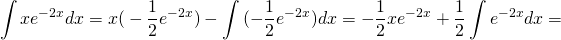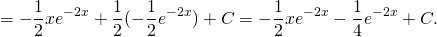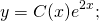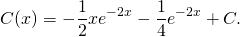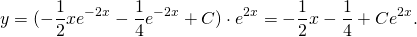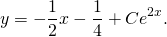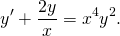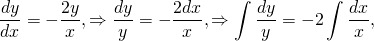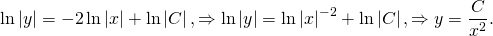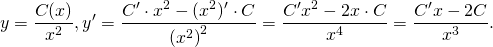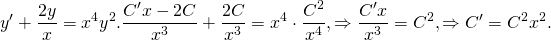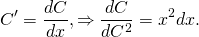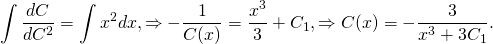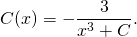Метод лагранжа для решения линейных дифференциальных уравнений первого порядка

Рассмотрим линейное неоднородное дифференциальное уравнение первого порядка:
(1) .
Существует три способа решения этого уравнения:

Рассмотрим решение линейного дифференциального уравнения первого порядка методом Лагранжа.

Видео:7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать

Метод вариации постоянной (Лагранжа)

В методе вариации постоянной мы решаем уравнение в два этапа. На первом этапе мы упрощаем исходное уравнение и решаем однородное уравнение. На втором этапе мы заменим постоянную интегрирования, полученную на первой стадии решения, на функцию. После чего ищем общее решение исходного уравнения.

Шаг 1 Решение однородного уравнения

Ищем решение однородного уравнения:

Это уравнение с разделяющимися переменными

Разделяем переменные — умножаем на dx , делим на y :

Интегрируем:

Интеграл по y — табличный:

Тогда

Потенцируем:

Заменим постоянную e C на C и уберем знак модуля, что сводится к умножению на постоянную ±1 , которую включим в C :

Шаг 2 Заменим постоянную C на функцию

Теперь заменим постоянную C на функцию от x :
C → u ( x )
То есть, будем искать решение исходного уравнения (1) в виде:
(2)
Находим производную.

По правилу дифференцирования сложной функции:
.
По правилу дифференцирования произведения:

.
Подставляем в исходное уравнение (1):
(1) ;

.
Два члена сокращаются:
;
.
Интегрируем:
.
Подставляем в (2):
.
В результате получаем общее решение линейного дифференциального уравнения первого порядка:
.

Видео:9. Метод вариации произвольной постоянной ( метод Лагранжа ). Линейные дифференциальные уравнения.Скачать

Пример решения линейного дифференциального уравнения первого порядка методом Лагранжа

Решаем однородное уравнение:

Разделяем переменные:

Умножим на :

Интегрируем:

Интегралы табличные:

Потенцируем:

Заменим постоянную e C на C и убираем знаки модуля:

Отсюда:

Заменим постоянную C на функцию от x :
C → u ( x )

Находим производную:
.
Подставляем в исходное уравнение:
;
;
Или:
;
.
Интегрируем:
;
Решение уравнения:
.

Общее решение уравнения:
.

Автор: Олег Одинцов . Опубликовано: 27-07-2012 Изменено: 01-03-2015

Видео:Математика без Ху!ни. Линейное неоднородное уравнение 1 порядка. Метод вариации постоянной.Скачать

Примеры на метод вариации произвольной постоянной

Метод вариации произвольной постоянной, или метод Лагранжа — еще один способ решения линейных дифференциальных уравнений первого порядка и уравнения Бернулли.

Линейные дифференциальные уравнения первого порядка — это уравнения вида y’+p(x)y=q(x). Если в правой части стоит нуль: y’+p(x)y=0, то это — линейное однородное уравнение 1го порядка. Соответственно, уравнение с ненулевой правой частью, y’+p(x)y=q(x), — неоднородное линейное уравнение 1го порядка.

Метод вариации произвольной постоянной (метод Лагранжа) состоит в следующем:

1) Ищем общее решение однородного уравнения y’+p(x)y=0: y=y*.

2) В общем решении С считаем не константой, а функцией от икса: С=С(x). Находим производную общего решения (y*)’ и в первоначальное условие подставляем полученное выражение для y* и (y*)’. Из полученного уравнения находим функцию С(x).

3) В общее решение однородного уравнения вместо С подставляем найденное выражение С(x).

Рассмотрим примеры на метод вариации произвольной постоянной. Возьмем те же задания, что и в примерах решения линейных дифференциальных уравнений методом Бернулли , сравним ход решения и убедимся, что полученные ответы совпадают.

1) y’=3x-y/x

Перепишем уравнение в стандартном виде (в отличие от метода Бернулли, где форма записи нам нужна была только для того, чтобы увидеть, что уравнение — линейное).

y’+y/x=3x (I). Теперь действуем по плану.

1) Решаем однородное уравнение y’+y/x=0. Это уравнение с разделяющимися переменными. Представляем y’=dy/dx, подставляем: dy/dx+y/x=0, dy/dx=-y/x. Обе части уравнения умножаем на dx и делим на xy≠0: dy/y=-dx/x. Интегрируем:

2) В полученном общем решении однородного уравнения будем считать С не константой, а функцией от x: С=С(x). Отсюда

Полученные выражения подставляем в условие (I):

Интегрируем обе части уравнения:

здесь С — уже некоторая новая константа.

3) В общее решение однородного уравнения y=C/x, где мы считали С=С(x), то есть y=C(x)/x, вместо С(x) подставляем найденное выражение x³+C: y=(x³+C)/x или y=x²+C/x. Получили такой же ответ, как и при решении методом Бернулли.

2) y’+y=cosx.

Здесь уравнение уже записано в стандартном виде, преобразовывать не надо.

1) Решаем однородное линейное уравнение y’+y=0: dy/dx=-y; dy/y=-dx. Интегрируем:

Чтобы получить более удобную форму записи, экспоненту в степени С примем за новую С:

Это преобразование выполнили, чтобы удобнее было находить производную.

2) В полученном общем решении линейного однородного уравнения считаем С не константой, а функцией от x: С=С(x). При этом условии

Полученные выражения y и y’ подставляем в условие:

Умножим обе части уравнения на

Интегрируем обе части уравнения по формуле интегрирования по частям, получаем:

Здесь С уже не функция, а обычная константа.

3) В общее решение однородного уравнения

подставляем найденную функцию С(x):

Получили такой же ответ, как и при решении методом Бернулли.

Метод вариации произвольной постоянной применим и для решения уравнений Бернулли .

y’x+y=-xy².

Приводим уравнение к стандартному виду: y’+y/x=-y² (II).

1) Решаем однородное уравнение y’+y/x=0. dy/dx=-y/x. Умножаем обе части уравнения на dx и делим на y: dy/y=-dx/x. Теперь интегрируем:

2) В полученном общем решении будем считать С не константой, а некоторой функций от x. При этом условии

Подставляем полученные выражения в условие (II):

Получили уравнение с разделяющимися переменными относительно С и x:

Здесь С — уже обычная константа. В процессе интегрирования писали вместо С(x) просто С, чтобы не перегружать запись. А в конце вернулись к С(x), чтобы не путать С(x) с новой С.

3) В общее решение однородного уравнения y=C(x)/x подставляем найденную функцию С(x):

Получили такой же ответ, что и при решении способом Бернулли.

Примеры для самопроверки:

1) Решаем однородное уравнение y’-2y=0. y’=dy/dx, отсюда dy/dx=2y, умножаем обе части уравнения на dx, делим на y и интегрируем:

Отсюда находим y:

2) В полученном решении С будем считать не константой, а функцией от x: C=C(x). Тогда

Выражения для y и y’ подставляем в условие (для краткости будем питать С вместо С(x) и С’ вместо C'(x)):

Для нахождения интеграла в правой части применяем формулу интегрирования по частям:

Теперь подставляем u, du и v в формулу:

3) Теперь подставляем в решение однородного

Отсюда получаем решение неоднородного уравнения:

2. Поделив обе части данного уравнения на x, приходим к уравнению

Это — уравнение Бернулли.

1) Решаем однородное уравнение y’+2y/x=0,

2) В этом решении заменяем константу С на функцию от x С(x), тогда

(для удобства пишем вместо С(x) просто С, но помним, что С здесь — функция от x). Теперь подставляем выражения для y и y’ в условие:

Интегрируем обе части уравнения:

Если ввести обозначение 3С1=С, то получим

3) В условие y=C(x)/x² подставляем найденное С(x):

Видео:Линейное дифференциальное уравнение первого порядка (1-x^2)*y'-xy=1Скачать

Метод вариации произвольной постоянной решения линейных неоднородных уравнений

Пример №1 . Найдём общее решение уравнения y» + 4y’ + 3y = 9e -3 x . Рассмотрим соответствующее однородное уравнение y» + 4y’ + 3y = 0. Корни его характеристического уравнения r 2 + 4r + 3 = 0 равны -1 и -3. Поэтому фундаментальная система решений однородного уравнения состоит из функций y₁ = e — x и y₂ = e -3 x . Решение неоднородного уравнения ищем в виде y = C₁(x)e — x + C₂(x)e -3 x . Для нахождения производных C’₁, C’₂ составляем систему уравнений (8)
C′₁·e -x +C′₂·e -3x =0
-C′₁·e -x -3C′₂·e -3x =9e -3x
решая которую, находим , Интегрируя полученные функции, имеем
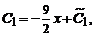
Окончательно получим

Пример №2 . Решить линейные дифференциальные уравнения второго порядка с постоянными коэффициентами методом вариации произвольных постоянных:

y(0) =1 + 3ln3
y’(0) = 10ln3

Решение:
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Решение уравнения будем искать в виде y = e rx . Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:
r 2 -6 r + 8 = 0
D = (-6) 2 — 4·1·8 = 4

Корни характеристического уравнения: r₁ = 4, r₂ = 2
Следовательно, фундаментальную систему решений составляют функции: y₁=e 4x , y₂=e 2x
Общее решение однородного уравнения имеет вид: y =C₁·e 4x +C₂·e 2x
Поиск частного решения методом вариации произвольной постоянной.
Для нахождения производных C’_i составляем систему уравнений:
C′₁·e 4x +C′₂·e 2x =0
C′₁(4e 4x ) + C′₂(2e 2x ) = 4/(2+e -2x )
Выразим C’₁ из первого уравнения:
C’₁ = -c₂e -2x
и подставим во второе. В итоге получаем:
C’₁ = 2/(e 2x +2e 4x )
C’₂ = -2e 2x /(e 2x +2e 4x )
Интегрируем полученные функции C’_i:
C₁ = 2ln(e -2x +2) — e -2x + C * ₁
C₂ = ln(2e 2x +1) – 2x+ C * ₂

Поскольку y =C₁·e 4x +C₂·e 2x , то записываем полученные выражения в виде:
C₁ = (2ln(e -2x +2) — e -2x + C * ₁) e 4x = 2 e 4x ln(e -2x +2) — e 2x + C * ₁ e 4x
C₂ = (ln(2e 2x +1) – 2x+ C * ₂)e 2x = e 2x ln(2e 2x +1) – 2x e 2x + C * ₂ e 2x
Таким образом, общее решение дифференциального уравнения имеет вид:
y = 2 e 4x ln(e -2x +2) — e 2x + C * ₁ e 4x + e 2x ln(2e 2x +1) – 2x e 2x + C * ₂ e 2x
или
y = 2 e 4x ln(e -2x +2) — e 2x + e 2x ln(2e 2x +1) – 2x e 2x + C * ₁ e 4x + C * ₂ e 2x

Найдем частное решение при условии:
y(0) =1 + 3ln3
y’(0) = 10ln3

Подставляя x = 0, в найденное уравнение, получим:
y(0) = 2 ln(3) — 1 + ln(3) + C * ₁ + C * ₂ = 3 ln(3) — 1 + C * ₁ + C * ₂ = 1 + 3ln3
Находим первую производную от полученного общего решения:
y’ = 2e 2x (2C₁ e 2x + C₂ -2x +4 e 2x ln(e -2x +2)+ ln(2e 2x +1)-2)
Подставляя x = 0, получим:
y’(0) = 2(2C₁ + C₂ +4 ln(3)+ ln(3)-2) = 4C₁ + 2C₂ +10 ln(3) -4 = 10ln3

Получаем систему из двух уравнений:
3 ln(3) — 1 + C * ₁ + C * ₂ = 1 + 3ln3
4C₁ + 2C₂ +10 ln(3) -4 = 10ln3
или
C * ₁ + C * ₂ = 2
4C₁ + 2C₂ = 4
или
C * ₁ + C * ₂ = 2
2C₁ + C₂ = 2
Откуда: C₁ = 0, C * ₂ = 2
Частное решение запишется как:
y = 2e 4x ·ln(e -2x +2) — e 2x + e 2x ·ln(2e 2x +1) – 2x·e 2x + 2·e 2x

📸 Видео

Дифференциальные уравнения, 4 урок, Линейные дифференциальные уравнения первого порядкаСкачать

Метод Бернулли. Метод Лагранжа (вариации произвольной постоянной). Линейное дифуравнение 1 порядкаСкачать

Метод Лагранжа. Решение линейного дифференциального уравнения первого порядка.Скачать

Метод Лагранжа & Метод Бернулли ★ Решение линейных неоднородных дифференциальных уравненийСкачать

19. Метод вариации произвольных постоянных. Линейные неоднородные диф уравнения 2-го порядкаСкачать

Линейные дифференциальные уравнения 1 порядка: метод Бернулии, метод ЛагранжаСкачать

Решите уравнение ★ y'-2y=e^(2x) ★ Линейное дифференциальное уравнение 1-го порядкаСкачать

Линейные неоднородные дифференциальные уравнения 1-го порядка. Метод Лагранжа. (ч.1)Скачать

13. Как решить дифференциальное уравнение первого порядка?Скачать

10. Уравнения БернуллиСкачать

Линейное дифференциальное уравнение Коши-ЭйлераСкачать

Поле направлений дифференциального уравнения первого порядкаСкачать

Уравнение Бернулли Метод БернуллиСкачать

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Линейные ДУ первого порядкаСкачать