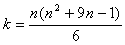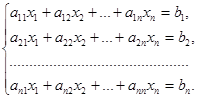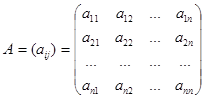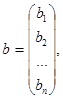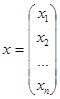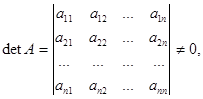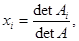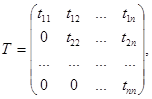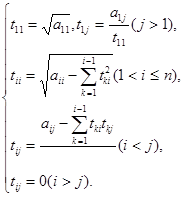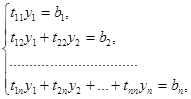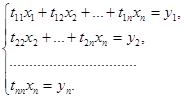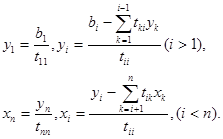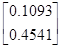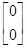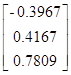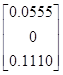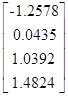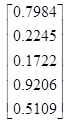Обсуждение и решение задач по математике, физике, химии, экономике
| Часовой пояс: UTC + 3 часа [ Летнее время ] | новый онлайн-сервис число, сумма и дата прописью |
| Метод квадратных корней для решения СЛАУ | ||||||||
|---|---|---|---|---|---|---|---|---|
| Название: Метод квадратных корней Раздел: Рефераты по математике Тип: контрольная работа Добавлен 08:40:32 17 апреля 2011 Похожие работы Просмотров: 1629 Комментариев: 19 Оценило: 2 человек Средний балл: 5 Оценка: неизвестно Скачать | |||||||
|
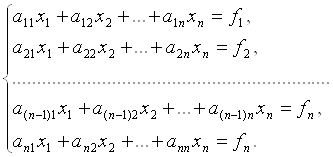
или в матричной форме
— столбец свободных членов и столбец неизвестных соответственно.
Если матрица А неособенная, т.е.
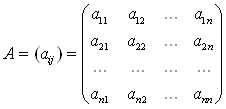
то система (1.1) имеет единственное решение. В этом случае решение системы (1.1) с теоретической точки зрения не представляет труда. Значения неизвестных xi (i=1,2,…n) могут быть получены по известным формулам Крамера
крамер квадратный корень матрица
где матрица Ai получается из матрицы А заменой ее i-го столбца столбцом свободных членов.
Но такой способ решения линейной системы с n неизвестными приводит к вычислению n + 1 определителей порядка n, что представляет собой весьма трудоемкую операцию при сколько-нибудь большом числе n.
Применяемые в настоящее время методы решения линейных систем можно разбить на две группы: точные и приближенные.
Точными методами называются такие методы, которые в предположении, что вычисления ведутся точно (без округлений), приводят к точным значениям неизвестных xi . Так как на практике все вычисления ведутся с округлениями, то и значения неизвестных, полученные точным методом, неизбежно будут содержать погрешности. К точным методам относятся, например, метод Гаусса, метод квадратных корней.
Приближенными методами называются такие методы, которые даже в предположении, что вычисления ведутся без округлений, позволяют получить решение системы (x1 , x2 , …, xn ) лишь с заданной точностью. Точное решение системы в этих случаях может быть получено теоретически как результат бесконечного процесса. К приближенным методам относятся метод простой итерации, метод Зейделя и др. Каждый из этих методов не всегда является сходящимся в применении к конкретному классу систем линейных уравнений.
Данная контрольная работа имеет следующую структуру: в начале рассматривается математическая постановка задачи для метода квадратных корней при решении систем линейных алгебраических уравнений. Затем производится реализация данного метода с помощью вычислительных средств ЭВМ, а именно прикладной программой Matlab 6.5. На примере реализации нескольких тестовых задач проводится анализ точности данного метода, а именно когда наиболее эффективно применять метод квадратных корней при решении систем линейных алгебраических уравнений. Анализ проводится на основе матрицы А (ее мерности, разреженности, обусловленности. Результаты, полученные на основе метода квадратных корней, приведены в конце данной работы. Также в работе представлен графический материал. По окончании проведения исследования работа завершается логическим заключением.
Метод квадратных корней используется для решения линейной системы
у которой матрица А симметрическая, т.е.
Метод является более экономным и удобным по сравнению с решением систем общего вида.
Решение системы осуществляется в два этапа.
Прямой ход. Представим матрицу А в виде произведения двух взаимно транспонированных треугольных матриц:
|
А = Т¢ Т,
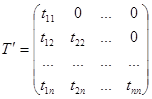
Перемножая матрицы T¢ и T и приравнивая матрице A, получим следующие формулы для определения tij :
|
После того, как матрица Т найдена, систему (1.2) заменяем двумя эквивалентными ей системами с треугольными матрицами
|
Обратный ход. Записываем в развернутом виде системы (1.5):
Отсюда последовательно находим
При вычислениях применяется обычный контроль с помощью сумм, причем при составлении суммы учитываются все коэффициенты соответствующей строки.
Заметим, что при действительных aij могут получиться чисто мнимые tij . Метод применим и в этом случае.
Для изучения данного метода было выбрано программное обеспечение: Matlab 6.5, в операционной системе WindowsXPProfessional. На этапе проектирования была создана программа Square (‘квадрат’). Входными переменными для данной программы является матрица A и соответствующая ей матрица B. Результатом выполнения данной программы является матрица X (выходная переменная), которая является решением системы линейных алгебраических уравнений.
Ниже описан алгоритм реализации метода квадратных корней на языке программирования в среде Matlab 6.5:
A=input(‘Введите матрицу A=’);
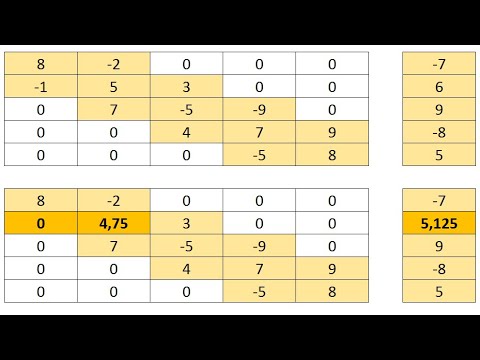
if i * — b (x * — полученное решение). Для этого рассмотрим разного рода матрицы:
— влияние мерности матрицы А;
Рассмотрим матрицы мерности 2´2, 3´3, 4´4 и 5´5. Зададим матрицу мерностью 2´2:
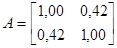
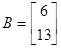
X =
ε =
Зададим матрицу размерностью 3´3:
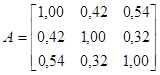
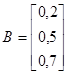
X =
ε =
Зададим матрицу размерностью 4´4:
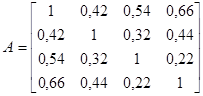
X =
ε =
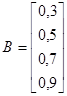
Зададим матрицу размерностью 5´5:
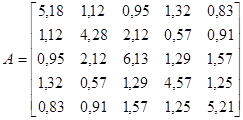
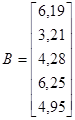
X =
ε =
Сравним полученные результаты, для этого проанализируем точность полученного решения. Результат мы можем оценить двумя способами 
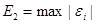
🌟 Видео
Решение систем уравнений второго порядка. 8 класс.Скачать

Решение системы уравнений методом Крамера 2x2Скачать

Решение системы линейных уравнений графическим методом. 7 класс.Скачать

2.1 Точные методы решения СЛАУ (Крамера, Гаусса, Жордана, прогонки)Скачать
Решение системы уравнений методом Крамера.Скачать

Решение системы уравнений методом ГауссаСкачать

Графический метод решения систем линейных уравнений 7 классСкачать

Система линейных уравнений. Общее решение. Метод ГауссаСкачать

15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

ПОСМОТРИ это видео, если хочешь решить систему линейных уравнений! Метод ПодстановкиСкачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

12. Метод Гаусса решения систем линейных уравнений. Часть 1.Скачать

СЛОЖИТЕ ДВА КОРНЯСкачать

Метод Гаусса решения систем линейных уравненийСкачать

Матричный метод решения систем уравненийСкачать

9 класс, 11 урок, Методы решения систем уравненийСкачать

Метод Ньютона (метод касательных) Пример РешенияСкачать

Как решают уравнения в России и СШАСкачать


 ,
, ,
, .
.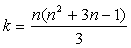 действий,
действий, , а
, а 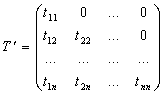 .
. (1.3)
(1.3) (1.5)
(1.5) (1.6)
(1.6) (1.7)
(1.7)