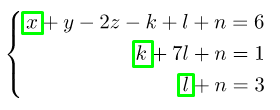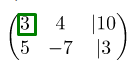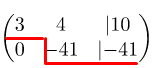Метод исключения переменных для решения систем уравнений

Метод Гаусса – идеальный вариант для решения систем линейных алгебраических уравнений (далее СЛАУ). Благодаря методу Гаусса можно последовательно исключать неизвестные путём элементарных преобразований. Метод Гаусса – это классический метод решения СЛАУ, который и рассмотрен ниже.

Карл Фридрих Гаусс – немецкий математик, основатель одноименного метода решения СЛАУ

Карл Фридрих Гаусс – был известным великим математиком и его в своё время признали «королём математики». Хотя название «метод Гаусса» является общепринятым, Гаусс не является его автором: метод Гаусса был известен задолго до него. Первое его описание имеется в китайском трактате «Математика в девяти книгах», который составлен между II в. до н. э. и I в. н. э. и представляет собой компиляцию более ранних трудов, написанных примерно в X в. до н. э.

Метод Гаусса – последовательное исключение неизвестных. Этот метод используется для решения квадратных систем линейных алгебраических уравнений. Хотя уравнения при помощи метода Гаусса решаются легко, но всё же студенты часто не могут найти правильное решение, так как путаются в знаках (плюсы и минусы). Поэтому во время решения СЛАУ необходимо быть предельно внимательным и только тогда можно легко, быстро и правильно решить даже самое сложное уравнение.

У систем линейных алгебраических уравнений есть несколько преимуществ: уравнение не обязательно заранее на совместность; можно решать такие системы уравнений, в которых число уравнений не совпадает с количеством неизвестных переменных или определитель основной матрицы равняется нулю; есть возможность при помощи метода Гаусса приводить к результату при сравнительно небольшом количестве вычислительных операций.

Видео:6 способов в одном видеоСкачать

Определения и обозначения

Как уже говорилось, метод Гаусса вызывает у студентов некоторые сложности. Однако, если выучить методику и алгоритм решения, сразу же приходит понимание в тонкостях решения.

Для начала систематизируем знания о системах линейных уравнений.

СЛАУ в зависимости от её элементов может иметь:

1. Одно решение;
2. много решений;
3. совсем не иметь решений.

В первых двух случаях СЛАУ называется совместимой, а в третьем случае – несовместима. Если система имеет одно решение, она называется определённой, а если решений больше одного, тогда система называется неопределённой.

Метод Крамера и матричный способ не подходят для решения уравнений, если система имеет бесконечное множество решений. Вот поэтому нам и нужен метод Гаусса, который поможет нам в любом случае найти правильное решение. К элементарным преобразованиям относятся:

• перемена мест уравнений системы;
• почленное умножение обеих частей на одно из уравнений на некоторое число, так, чтобы коэффициенты при первой переменной в двух уравнениях были противоположными числами;
• сложение к обеим частям одного из уравнений определённых частей другого уравнения.

Итак, когда мы знаем основные правила и обозначения, можно приступать к решению.

Теперь рассмотрим, как решаются системы методом Гаусса на простом примере:

где а, в, с – заданные коэффициенты, d – заданные свободные члены, x, y, z – неизвестные. Коэффициенты и свободные члены уравнения можно называть его элементами.

Если = = = , тогда система линейных алгебраических уравнений называется однородной, в другом случае – неоднородной.

Множественные числа , , называются решением СЛАУ, если при подстановке , , в СЛАУ получим числовые тождества.

Система, которую мы написали выше имеет координатную форму. Если её переделать в матричную форму, тогда система будет выглядеть так:

– это основная матрица СЛАУ.

– матрица столбец неизвестных переменных.

– матрица столбец свободных членов.

Если к основной матрице добавить в качестве – ого столбца матрицу-столбец свободных членов, тогда получится расширенная матрица систем линейных уравнений. Как правило, расширенная матрица обозначается буквой , а столбец свободных членов желательно отделить вертикальной линией от остальных столбцов. То есть, расширенная матрица выглядит так:

Если квадратная матрица равна нулю, она называется вырожденная, а если – матрица невырожденная.

Если с системой уравнений:

Произвести такие действия:

• умножать обе части любого из уравнений на произвольное и отличное от нуля число ;
• менять местами уравнения;
• к обеим частям любого из уравнений прибавить определённые части другого уравнения, которые умножаются на произвольное число ,

тогда получается эквивалентная система, у которой такое же решение или нет решений совсем.

Теперь можно перейти непосредственно к методу Гаусса.

Нужна помощь в написании работы?

Написание учебной работы за 1 день от 100 рублей. Посмотрите отзывы наших клиентов и узнайте стоимость вашей работы.

Видео:Решение системы линейных уравнений методом исключения | МатематикаСкачать

Простейшие преобразования элементов матрицы

Мы рассмотрели основные определения и уже понимаем, чем нам поможет метод Гаусса в решении системы. Теперь давайте рассмотрим простую систему уравнений. Для этого возьмём самое обычное уравнение, где и используем решение методом Гаусса:

Из уравнения запишем расширенную матрицу:

Из данной матрицы видно, по какому принципу она записана. Вертикальную черту не обязательно ставить, но просто так удобнее решать систему.

На матрице, которая написана выше рассмотрим, какие существуют элементарные преобразования:

1. В матрице строки можно переставлять местами. Например, в нашей матрице спокойно можно переставить первую и вторую строки:

.

2. Если в матрице имеются (или появились) пропорциональные строки (одинаковые), тогда необходимо оставить всего лишь одну строку, а остальные убрать (удалить).

3. Если в ходе преобразований в матрице появилась строка, где находятся одни нули, тогда такую строку тоже нужно удалять.

4. Строку матрицы можно умножать (делить) на любое число, которое отличное от нуля. Такое действие желательно проделывать, так как в будущем проще преобразовывать матрицу.

5. Сейчас рассмотрим преобразование, которое больше всего вызывает затруднение у студентов. Для этого возьмём изначальную нашу матрицу:

Для удобства умножаем первую строку на (-3):

Теперь ко второй строке прибавляем первую строку, которую умножали на -3. Вот что у нас получается:

В итоге получилось такое преобразование:

Теперь для проверки можно разделить все коэффициенты первой строки на те же и вот что получается:

В матрице верхняя строка преобразовалась:

Первую строку делим на и преобразовалась нижняя строка:

И верхнюю строку поделили на то же самое число :

Как вы можете убедиться, в итоге строка, которую мы прибавляли ни капельки не изменилась, а вот вторая строка поменялась. ВСЕГДА меняется только та строка, к которой прибавляются коэффициенты.

Мы расписали в таких подробностях, чтобы было вам понятно, откуда какая цифра взялась. На практике, например, на контрольной или экзамене матрица так подробно не расписывается. Как правило, в задании решение матрицы оформляется так:

.

Видео:Решение системы уравнений методом ГауссаСкачать

Алгоритм решения методом Гаусса пошагово

После того, как мы рассмотрели простейшие преобразования, в которых на помощь пришёл метод Гаусса, можем вернуться к нашей системе, которую уже разложили по полочкам и пошагово распишем:

Шаг 1. Переписываем систему в виде матрицы

Шаг 2. Преобразовываем матрицу: вторую строку в первом столбце приводим к нулю

Как мы привели вторую строку в первом столбце к нулю описано выше. Напомним, что первую строку умножали на и вторую строку прибавили к первой , умноженной на .

Шаг 3. Приводим матрицу к ступенчатому виду

Теперь вторую строку можно поделить на 2 и получается:

Верхнюю строку делим на и приводим матрицу к ступенчатому виду:

Когда оформляют задание, так и отчёркивают простым карандашом для упрощения работы, а также обводят те числа, которые стоят на “ступеньках”. Хотя в учебниках и другой литературе нет такого понятия, как ступенчатый вид. Как правило, математики такой вид называют трапециевидным или треугольным.

Шаг 4. Записываем эквивалентную систему

После наших элементарных преобразований получилась эквивалентная система:

Шаг 5. Производим проверку (решение системы обратным путём)

Теперь систему нужно решить в обратном направлении, то есть обратным ходом, начиная с последней строки.:

находим : ,

,

.

После находим :

,

.

.

Как видим, уравнение решено правильно, так как ответы в системе совпадают.

Видео:Решение системы линейных уравнений методом ГауссаСкачать

Решение систем линейных уравнений методом Гаусса, в которых основная матрица невырожденная, а количество в ней неизвестных равняется количеству уравнений

Как мы уже упоминали, невырожденная матрица бывает тогда, когда . Разберём систему уравнений невырожденной матрицы, где уравнений по количеству столько же, сколько и неизвестных. Эту систему уравнений решим другим способом.

Дана система уравнений:

Для начала нужно решить первое уравнение системы относительно неизвестной переменной . Далее подставим полученное выражение сначала во второе уравнение, а затем в третье, чтобы исключить из них эту переменную.

Теперь переходим ко второму уравнению системы относительно и полученный результат подставим в третье уравнение.. Это нужно для того, чтобы исключить неизвестную переменную :

Из последнего, третьего уравнения мы видим, что . Из второго уравнения находим . И последнее, находим первое уравнение .

Итак, мы нашли все три неизвестных при помощи последовательного исключения. Такой процесс называют – прямой ход метода Гаусса. Когда последовательно находятся неизвестные переменные, начиная с последнего уравнения, называется обратным ходом метода Гаусса.

Когда выражается через и в первом уравнении, а затем подставляется полученное выражение во второе или третье уравнения, тогда, чтобы привести в к такому же результату, необходимо проделать такие действия:

• берём второе уравнение и к его левой и правой частям прибавляем определённые части из первого уравнения, которые умножаются на ,
• берём третье уравнение и к его левой и правой частям прибавляем определённые части из первого уравнения, которые умножаются на .

И действительно, благодаря такой процедуре у нас есть возможность исключать неизвестную переменную со второго и третьего уравнения системы:

Возникают нюансы с исключением неизвестных переменных тогда, когда в уравнении системы нет каких-либо неизвестных переменных. Рассмотрим такую систему:

В этой системе в первом уравнении нет переменной и поэтому у нас нет возможности решить первое уравнение системы относительно , чтобы исключить данную переменную из остальных уравнений. В таком случае выход есть. Нужно всего лишь уравнения переставить местами.

Так как мы описываем уравнения системы, в которых определитель основных матриц отличен от нуля, тогда всегда есть такое уравнение, в котором есть необходимая нам переменная и это уравнение мы можем поставить туда, куда нам нужно.

В примере, который мы рассматриваем, достаточно всего лишь поменять местами первое и второе уравнение.

Теперь мы можем спокойно разрешить первое уравнение относительно переменной и убрать (исключить) из остальных уравнений в системе. Вот и весь принцип работы с такими, на первый взгляд, сложными системами.

Видео:Решение систем уравнений методом сложенияСкачать

Решение систем линейных уравнений методом Гаусса, в которых основная матрица вырожденная, а количество в ней неизвестных не совпадает с количеством уравнений

Метод Гаусса помогает решать системы уравнений, у которых основная матрица прямоугольная или квадратная, но основная вырожденная матрица может совсем не иметь решений, иметь бесконечное множество решений или иметь всего лишь одно единственное решение.

Рассмотрим, как при помощи метода Гаусса устанавливается совместность или несовместность систем линейных уравнений. В случае, если есть совместность определим все решения или одно решение.

В принципе, исключать неизвестные переменные можно точно так, как описано выше. Однако, есть некоторые непонятные ситуации, которые могут возникнуть в ходе решения:

1. На некоторых этапах в момент исключения неизвестных переменных некоторые уравнения могут обратиться в тождества . В данном случае такие уравнения лишние в системе и их можно смело полностью убирать, а затем продолжать решать уравнение методом Гаусса.

Например, вам попалась подобная система:

У нас получается такая ситуация

Как видим, второе уравнение . Соответственно, данное уравнение мы можем из системы удалить, так как оно без надобности.

Дальше можно продолжать решение системы линейных алгебраических уравнений уравнений традиционным методом Гаусса.

2. При решении уравнений прямым ходом методом Гаусса могут принять не только одно, но и несколько уравнений такой вид: , где – число, которое отличное от нуля. Это говорит о том, что такое уравнение никогда не сможет превратиться в тождество даже при любых значениях неизвестных переменных. То есть, можно выразить по-другому. Если уравнение приняло вид, значит система несовместна, то есть, не имеет решений. Рассмотрим на примере:

Для начала необходимо исключить неизвестную переменную из всех уравнений данной системы, начиная со второго уравнения. Для этого нужно прибавить к левой и правой частям второго, третьего, четвёртого уравнения части (левую и правую) первого уравнения, которые соответственно, умножаются на (-1), (-2), (-3). Получается:

В третьем уравнении получилось равенство . Оно не подходит ни для каких значений неизвестных переменных , и , и поэтому, у данной системы нет решений. То есть, говорится, что система не имеет решений.

3. Допустим, что при выполнении прямого хода методом Гаусса нам нужно исключить неизвестную переменную , и ранее, на каком-то этапе у нас уже исключалась вместе с переменной . Как вы поступите в таком случае? При таком положении нам нужно перейти к исключению переменной . Если же уже исключались, тогда переходим к , и т. д.

Рассмотрим систему уравнений на таком этапе, когда уже исключилась переменная :

Такая система уравнений после преобразования выглядит так:

Вы наверное уже обратили внимание, что вместе с исключились и . Поэтому решение методом Гаусса продолжаем исключением переменной из всех уравнений системы, а начнём мы с третьего уравнения:

Чтобы завершить уравнение прямым ходом метода Гаусса, необходимо исключить последнюю неизвестную переменную из последнего уравнения:

Допусти, что система уравнений стала:

В этой системе нет ни одного уравнения, которое бы сводилось к . В данном случае можно было бы говорить о несовместности системы. Дальше непонятно, что же делать? Выход есть всегда. Для начала нужно выписать все неизвестные, которые стоят на первом месте в системе:

В нашем примере это , и . В левой части системы оставим только неизвестные, которые выделены зелёным квадратом а в правую перенесём известные числа, но с противоположным знаком. Посмотрите на примере, как это выглядит:

Можно придать неизвестным переменным с правой части уравнений свободные (произвольные) значения: , , , где , , – произвольные числа.

Теперь в правых частях уравнений нашей системы имеются числа и можно приступать к обратному ходу решения методом Гаусса.

В последнем уравнении системы получилось: , и теперь мы легко найдём решение в предпоследнем уравнении: , а из первого уравнения получаем:

= =

В итоге, получился результат, который можно и записать.

Ответ

,

,

,

,

,

.

Видео:Алгебра 9 класс. Решение систем уравнений методом замены переменныхСкачать

Примеры решения методом Гаусса

Выше мы подробно расписали решение системы методом Гаусса. Чтобы закрепить материал, решим несколько примеров, в которых опять нам поможет метод Гаусса. Соответственно, начнём с самой простой системы.

Задача

Решить систему линейных алгебраических уравнений методом Гаусса:

Решение

Выписываем матрицу, куда добавляем столбец свободных членов:

Прежде всего мы смотрим на элемент, который находится в матрице в левом верхнем углу (первая строка, первый столбец). Для наглядности выделим цифру зелёным квадратом. На этом месте практически всегда стоит единица:

Так как мы должны использовать подходящее элементарное преобразование строк и сделать так, чтобы элемент, который находится в матрице под выделенной цифрой превратился в . Для этого можно ко второй строке прибавить первую строку и умножить на .Однако, не сильно хочется работать с дробями, поэтому давайте постараемся этого избежать. Для этого нужно вторую строку умножить на (разрешающий элемент данного шага).

Соответственно, первая строка остаётся неизменной, а вторая поменяется:

Подбираем такое элементарное преобразование строк, чтобы во второй строке в первом столбце образовался . Для этого первую строку нужно умножить на и только после этого ко второй строке прибавить изменённую после умножения на вторую строку. Вот что получилось:

. Теперь прибавляем со второй строки первую строку . У нас получился , который записываем во вторую строку в первый столбец. Также решаем и остальные элементы матрицы. Вот что у нас получилось:

Как всегда у нас первая строка осталась без изменений, а вторая с новыми числами.

Итак, у нас получился ступенчатый вид матрицы:

Записываем новую систему уравнений:

Для проверки решаем систему обратным ходом. Для этого находим сначала :

Так как найден, находим :

.

Подставляем в изначальную нашу систему уравнений найденные и :

и .

Как видите из решения, система уравнений решена верно. Запишем ответ.

Ответ

Выше мы решали систему уравнений в двумя неизвестными, а теперь рассмотрим систему уравнений с тремя неизвестными.

Задача

Решить систему уравнений методом Гаусса:

Решение

Составляем матрицу, куда вписываем и свободные члены:

Что нам надо? Чтобы вместо цифры 2 появился 0. Для этого подбираем ближайшее число. Например, можно взять цифру -2 и на неё перемножить все элементы первой строки. Значит, умножаем , а потом прибавляем, при этом задействуем вторую строку: . В итоге у нас получился нуль, который записываем во вторую строку в первый столбец. Затем , и . Аналогично, и . И умножаем свободный член . Так и запишем следующую матрицу. Не забывайте, что первая строка остаётся без изменений:

Дальше необходимо проделать те же самые действия по отношению к третьей строке. То есть, первую строку нужно умножать не на (-2), а на цифру 3, так как и в третьей строке нужно коэффициенты привести у нулю. Также первую строку умножаем на 3 и прибавляем третью строку. Получается так:

Теперь нужно обнулить элемент 7, который стоит в третьей строке во втором столбце. Для этого выбираем цифру (-7) и проделываем те же действия. Однако, необходимо задействовать вторую строку. То есть, вторую строку умножаем на (-7) и прибавляем с третьей строкой. Итак, . Записываем результат в третью строку. Такие же действия проделываем и с остальными элементами. Получается новая матрица:

В результате получилась ступенчатая система уравнений:

Сначала находим : ,

.

Обратный ход:

Итак, уравнение системы решено верно.

Ответ

,

,

.

Система с четырьмя неизвестными более сложная, так как в ней легко запутаться. Попробуем решить такую систему уравнений.

Задача

Решите систему уравнений методом Гаусса:

Решение

В уравнении , то есть – ведущий член и пусть ≠ 0

Из данного уравнения составим расширенную матрицу:

Теперь нужно умножить последние три строки (вторую, третью и четвёртую) на: , , . Затем прибавим полученный результат ко второй, третьей и четвёртой строкам исключаем переменную из каждой строки, начиная не с первой, а не со второй. Посмотрите, как изменилась наша новая матрица и в теперь стоит 0.

Поменяем вторую и третью строку местами и получим:

Получилось так, что = b и тогда, умножая вторую строку на (-7/4) и результат данной строки, прибавляя к четвёртой, можно исключить переменную из третьей и четвёртой строк:

Получилась такая матрица:

Также, учитывая, что = , умножим третью строку на: 13,5/8 = 27/16, и, полученный результат прибавим к четвёртой, чтобы исключить переменную и получаем новую систему уравнений:

Теперь необходимо решить уравнение обратным ходом и найдём из последнего, четвёртого уравнения ,

из третьего: = = =

второе уравнение находим: = = = 2,

из первого уравнения: = .

Значит, решение системы такое: (1, 2, -1, -2).

Ответ

,

,

,

.

Добавим ещё несколько примеров для закрепления материла, но без такого подробного описания, как предыдущие системы уравнений.

Задача

Решить систему уравнений методом Гаусса:

Решение

Записываем расширенную матрицу системы:

Сначала смотрим на левое верхнее число:

Как выше уже было сказано, на этом месте должна стоять единица, но не обязательно. Производим такие действия: первую строку умножаем на -3, а потом ко второй строке прибавляем первую:

Производим следующие действия: первую строку умножаем на -1. Затем к третьей строки прибавляем вторую:

Теперь вторую строку умножаем на 1, а затем к третьей строке прибавляем вторую:

Получился ступенчатый вид уравнения:

,

,

,

,

.

.

Ответ

,

,

.

Видео:Решение систем уравнений методом сложенияСкачать

Заключение

Итак, вы видите, что метод Гаусса – интересный и простой способ решения систем линейных алгебраических уравнений. Путём элементарных преобразований нужно из системы исключать неизвестные переменные, чтобы систему превратить в ступенчатый вид. Данный метод удобен тем, что всегда можно проверить, правильно ли решено уравнение. Нужно просто подставить найденные неизвестные в изначальную систему уравнений.

Если элементы определителя не равняются нулю, тогда лучше обратиться к методу Крамера, а если же элементы нулевые, тогда такие системы очень удобно решать благодаря методу Гаусса.

Предлагаем ещё почитать учебники, в которых также описаны решения систем методом Гаусса.

Литература для общего развития:

Видео:Математика без Ху!ни. Метод Гаусса.Скачать

VMath

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Системы линейных уравнений

Обозначим через $ mathbb A_ $ любое из множеств $ mathbb Q_, mathbb R_ $ или $ mathbb C_ $.

Примеры систем уравнений над $ mathbb R $.

Относительно числа $ m_ $ уравнений не делается ни какого предположения: оно может быть меньше, больше или равно числу переменных $ n_ $. Если $ m_>n $ то система называется переопределенной. Решением системы уравнений называется любой набор значений переменных $ x_1=alpha_,dots, x_n = alpha_n $, обращающий каждое из уравнений в истинное равенство. Система называется совместной если она имеет хотя бы одно решение и несовместной в противном случае.

Можно доказать (см. результаты ☟ НИЖЕ ), что все возможности для произвольной системы ограничиваются следующими вариантами:

1. система совместна и имеет единственное решение;

2. cистема совместна и имеет бесконечное множество решений;

3. cистема несовместна.

При этом все решения будут находиться в том же множестве $ mathbb A_ $, что и коэффициенты системы.

Видео:МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать

Матричная форма записи

Для системы линейных уравнений относительно переменных $ x_1,x_2,dots,x_n $ $$ left< begin a_x_1 &+a_x_2&+ ldots&+a_x_n &=b_1,\ a_x_1 &+a_x_2&+ ldots&+a_x_n &=b_2,\ dots & & & & dots \ a_x_1 &+a_x_2&+ ldots&+a_x_n &=b_m. end right. $$ матрицей системы называется матрица $$ A=left( begin a_ & a_ & dots & a_ \ a_ & a_ & dots & a_ \ dots &&& dots \ a_ & a_ & dots & a_ end right)_ ; $$ cтолбец $$ = left( begin b_ \ b_ \ vdots \ b_ end right) $$ называется столбцом правых частей системы, а столбец $$ X= left( begin x_ \ x_ \ vdots \ x_ end right) $$ — столбцом неизвестных. Используя правило умножения матриц, систему можно записать в матричном виде: $$ AX= . $$ Любое решение $ x_1=alpha_1,dots,x_n=alpha_n $ системы можно также записать в виде столбца: $$ X=left( begin alpha_1 \ vdots \ alpha_n end right) in mathbb A^n . $$ Матрица, составленная из всех коэффициентов системы уравнений: $$ [A mid mathcal B ]= left( begin a_ & a_ & dots & a_ & b_1 \ a_ & a_ & dots & a_ & b_2 \ dots &&& & dots \ a_ & a_ & dots & a_ & b_m end right)_ , $$ т.е. конкатенацией матрицы $ A_ $ и столбца правых частей $ _ $ называется расширенной матрицей системы л.у.

Видео:Решение системы уравнений методом Гаусса 4x4Скачать

Исключение переменных (метод Гаусса)

метода достаточно проста.

Пример. Решить систему уравнений $$ left< begin 2x_1&-3x_2&-x_3&=3 \ 4x_1&-3x_2&-5x_3&=6 \ 3x_1&+5x_2&+9x_3&=-8 end right. $$

Решение. Выразим из первого уравнения $ x_ $ $$ x_1=frac x_2+frac x_3 + frac $$ и подставим в оставшиеся уравнения $$ 4 left(frac x_2+frac x_3 + fracright) -3,x_2-5,x_3=6 <coloriff > 3x_2-3x_3 = 0 $$ $$ <coloriff > x_2-x_3=0 ; $$ $$ 3 left(frac x_2+frac x_3 + fracright) +5x_2+9x_3=-8 <coloriff > frac x_2 +fracx_3=-frac $$ $$ <coloriff > 19x_2 +21x_3=-25 . $$ Два получившихся уравнения не зависят от неизвестной $ x_ $ — она оказалась исключенной из этих уравнений. Иными словами, мы получили новую подсистему уравнений $$ left< begin x_2&-x_3&=0 \ 19x_2&+21x_3&=-25, end right. $$ которой должны удовлетворять неизвестные $ x_ $ и $ x_ $. Продолжаем действовать по аналогии: выразим из первого уравнения $ x_ $ через $ x_ $: $$x_2=x_3 $$ и подставим во второе: $$ 40 x_3 =-25 iff x_3=-frac . $$ Итак, значение одной компоненты решения получено. Для нахождения оставшихся подставим значение $ x_ $ в полученные по ходу решения соотношения: $$ x_2=x_3=-frac Rightarrow x_1=frac x_2+frac x_3 + frac=frac . $$

Ответ. $ x_=1/4, x_2=-5/8, x_3=-5/8 $.

Теперь осталось формализовать изложенную идею метода (сформулировав допустимые правила действия над уравнениями — те, что в принципе, очевидны из здравого смысла ), а также исследовать возможные последствия его применения к системам общего вида.

Исключение переменных

Элементарными преобразованиями системы л.у. называются преобразования следующих трех типов:

1. перестановка двух уравнений;

2. умножение обеих частей уравнения на любое отличное от нуля число;

3. прибавление к одному уравнению любого другого, умноженного на произвольное число: пара уравнений $$ begin a_x_1 +a_x_2+ ldots+a_x_n &=&b_j,\ a_x_1 +a_x_2+ ldots+a_x_n &=&b_k end $$ заменяется парой $$ begin (a_+ <colorlambda > a_) x_1 &+ (a_+ <colorlambda > a_) x_2 &+ ldots &+ (a_+ <colorlambda > a_) x_n &=&b_j + <colorlambda > b_k, , \ a_x_1 &+a_x_2&+ ldots &+a_x_n &=&b_k , . end $$

Теорема. Любое элементарное преобразование системы л.у. переводит эту систему в ей эквивалентную, т.е. имеющую то же множество решений, что и исходная.

Задача. С помощью элементарных преобразований привести систему л.у. к наиболее простому виду: такому, из которого легко было бы установить множество решений.

Предположим, что первое уравнение системы содержит явно неизвестную $ x_ $, т.е. $ a_^ ne 0 $. Исключим эту неизвестную из всех оставшихся уравнений. С этой целью вычтем из второго уравнения первое, домноженное на $ a_/a_^ $. Получим $$left(a_- frac<a_><a_> a_ right)x_2 + dots + left(a_- frac<a_><a_> a_ right)x_n = b_2 — frac<a_><a_> b_1 , $$ Аналогичное преобразование — вычитание из третьего уравнения системы первого, умноженного на $ a_/a_^ $, позволяет исключить $ x_ $ из этого уравнения, т.е. заменить его на $$left(a_- frac<a_><a_> a_ right)x_2 + dots + left(a_- frac<a_><a_> a_ right)x_n = b_3 — frac<a_><a_> b_1 . $$ Продолжаем процесс далее. В конечном итоге исключаем $ x_ $ из всех уравнений кроме первого: $$ left< begin a_x_1 &+a_x_2&+ ldots&+a_x_n &=b_1,\ &a_^x_2&+ ldots&+a_^x_n &=b_2^,\ &dots & & & dots \ &a_^x_2&+ ldots&+a_^x_n &=b_m^. end right. npu begin a_^ &= & displaystyle a_ — frac<a_a_><a_> ,\ b_j^ &= & displaystyle b_j — frac<a_b_1><a_> . end $$ Полученная система эквивалентна исходной системе, однако она имеет более простой вид: в ней выделилась подсиcтема $$ left< begin a_^x_2&+ ldots&+a_^x_n &=b_2^,\ dots & & & dots \ a_^x_2&+ ldots&+a_^x_n &=b_m^, end right. $$ которая не зависит от переменной $ x_ $. К этой новой подсистеме можно применить те же рассуждения, что и к исходной системе, поставив теперь целью исключение переменной $ x_ $.

Понятно, что процесс исключения может быть продолжен и далее. Теперь посмотрим, где он может прерваться. Может так случиться, что очередная, $ ell_ $-я подсистема имеет коэффициент $ a_^ $ равным нулю, что не позволит алгоритму идти дальше — т.е. исключить переменную $ x_^ $ из оставшихся уравнений (в принципе, такое могло случиться уже на первом шаге, если бы коэффициент $ a_^ $ был бы равен нулю). Возможные варианты дальнейших действий:

1. если хотя бы один коэффициент при $ x_^ $ в одном из оставшихся уравнений отличен от нуля: $ a_^ne 0^ $, то это уравнение переставляется с $ ell_ $-м;

2. если при всех $ jge ell^ $ коэффициенты $ a_^ $ равны нулю, то переменная $ x_^ $ не входит ни в одно оставшееся уравнение, и можно перейти к исключению переменной $ x_^ $.

Поскольку число переменных конечно, то алгоритм исключения должен завершиться за конечное число шагов. Чем он может завершиться? Окончательная система должна иметь вид: $$ left< begin a_x_1 +&a_x_2&+ ldots& +a_<1 >x_& +a_ <1 ,+1>x_<+1>&+ ldots + & a_x_n &=b_1,\ &a_^x_2&+ ldots& +a_<2 >^ x_& +a_<2 ,+1>^ x_<+1>&+ ldots + & a_^ x_n &=b_2^,\ & & ddots & & & & & dots \ & & & a_ <>^<[-1]>x_ & + a_ <, +1>^<[-1]>x_<+1>& + ldots + & a_ <,n>^<[-1]>x_n &=b_^<[-1]>, \ & & & & & & 0 &=b_<+1>^<[-1]>, \ & & & & & & dots & \ & & & & & & 0 &=b_^<[-1]>, \ end right. $$ при $ le n_ $. Заметим, что все коэффициенты этой системы будут принадлежать тому же множеству, что и коэффициенты исходной системы.

Предположение . Мы будем считать, что каждое из первых $ _ $ уравнений системы содержит в своей левой части хотя бы одну переменную с ненулевым коэффициентом.

Процесс получения системы такого вида из исходной системы уравнений называется прямым ходом метода Гаусса.

Исторический комментарий о Гауссе ☞ ЗДЕСЬ.

Установление множества решений

Теорема. Если хотя бы одно из чисел $ b_<+1>^<[-1]>,dots , b_^<[-1]> $ отлично от нуля, то исходная система линейных уравнений будет несовместной.

Для простоты мы будем иллюстрировать наши рассуждения на системах л.у. над $ mathbb R_ $, в этом же множестве искать решения. Каждое из преобразований метода Гаусса будем обозначать $ to_ $.

Пример. Решить систему л.у.

$$ left< begin x_1&+x_2&-3, x_3 =& -1 \ 2,x_1&+x_2&-2, x_3 =& 1 \ x_1&+x_2&+ x_3 =& 3 \ x_1&+2,x_2&-3, x_3 =& 1. end right. $$

Решение. $$ to left< begin x_1&+x_2&-3, x_3 =& -1 \ &-x_2&+4, x_3 =& 3 \ &&4, x_3 =& 4 \ &x_2&=& 2 end right. to left< begin x_1&+x_2&-3, x_3 =& -1 \ &-x_2&+4, x_3 =& 3 \ &&4, x_3 =& 4 \ &&4, x_3=& 5 end right. to $$ $$ to left< begin x_1&+x_2&-3, x_3 =& -1 \ &-x_2&+4, x_3 =& 3 \ &&4, x_3 =& 4 \ &&0=& 1 end right. $$ Последнее равенство абсолютно противоречиво.

Ответ. Система несовместна.

Пусть теперь $ b_<+1>^<[-1]>=0,dots, b_^<[-1]>=0 $. Возможны два случая: $ =n_ $ и $ предположения , имеем $ a_^ ne 0 $. Но тогда, поскольку система является конечной стадией прямого хода метода Гаусса, то и все коэффициенты $ a_^, dots, a_^, a_ $ должны быть отличны от нуля — в противном случае метод Гаусса не остановился бы на системе такого вида; он называется треугольным: Из последнего уравнения системы можно однозначно установить значение $ x_ $: $$x_n=b_n^ big/ a_^ .$$ Далее, подставляя это значение в $ (n-1) $-е уравнение системы, выражаем $ x_ $: $$ x_= frac<b_^ — a_^x_>< a_^>= frac< b_^ — a_^ b_n^ Big/ a_^>< a_^> . $$ Подставляем полученные значения для $ x_ $ и $ x_ $ в $ (n-2)_ $-е уравнение системы, выражаем $ x_ $, и т.д., в конце концов приходим к первому уравнению, из которого выражаем $ x_ $ если ранее уже получены выражения для $ x_2,dots,x_ $.

Теорема. Если прямой ход метода Гаусса заканчивается треугольной системой, т.е. $ mathfrak r = n_ $ и $ b_<+1>^<[-1]>=0,dots, b_^<[-1]>=0 $, то исходная система линейных уравнений имеет единственное решение.

Пример. Решить систему л.у.

$$ left< begin x_1&+3,x_2&+ x_3 =&5 \ 2,x_1&+x_2&+ x_3 =& 2 \ x_1&+x_2&+ 5,x_3 =& -7 \ 2,x_1&+3,x_2&-3, x_3 =& 14. end right. $$

Ответ. $ x_1=1,, x_=2,, x_3=-2 $ .

Исследуем теперь случай $ 1) : На основании предположения , в $ $-м уравнении этой системы имеется хотя бы один ненулевой коэффициент в левой части, пусть $ a_ <>^<[-1]>ne 0 $ — первый из них. Если $ =n $, то из этого уравнения однозначно определится $ x_ $ $$ x_n=alpha_n = b_^<[-1]> big/ a_ <n>^<[-1]> . $$ Если же $ предположения , в этом уравнении имеется хотя бы один ненулевой коэффициент в левой части; пусть $ a_<-1, >^<[-2]>ne 0_ $ — первый из них. Поскольку мы преположили, что система является конечной стадией прямого хода метода Гаусса, то $ по крайней мере две переменные, значения которых еще не были зафиксированы на предыдущих шагах. Это следует из предположения, что число уравнений $ _ $ меньше числа неизвестных $ n_ $. Такое уравнение допускает бесконечное число решений, любое из которых в ходе дальнейших шагов может быть «доделано» до решения системы.

Теорема. Если прямой ход метода Гаусса заканчивается трапециевидной системой, т.е. $ mathfrak r 2) матрицы $ A_ $ (третьего порядка). Понятие определителя распространяется и на квадратные матрицы бóльших порядков; образно говоря, определитель — это функция элементов матрицы, отвечающая за единственность решения системы уравнений.

Дальнейший матричный анализ метода Гаусса ☞ ЗДЕСЬ.

Видео:Решение системы уравнений методом Гаусса. Бесконечное множество решенийСкачать

Формулы Крамера

Рассмотрим систему линейных уравнений с квадратной матрицей $ A_ $, т.е. такую, у которой число уравнений совпадает с числом неизвестных.

Теорема. Cистема

$$ left<begin a_x_1 +a_x_2+ldots+a_x_n &=&b_1\ a_x_1 +a_x_2+ldots+a_x_n &=&b_2\ ldots& & ldots \ a_x_1 +a_x_2+ldots+a_x_n &=&b_n endright. $$ имеет единственное решение тогда и только тогда, когда определитель матрицы этой системы отличен от нуля: $$ left| begin a_ & a_ & dots & a_ \ a_ & a_ & dots & a_ \ dots &&& dots \ a_ & a_ & dots & a_ end right| ne 0 . $$ В этом случае решение можно вычислить по формулами Крамера 3) : $$ x_k =frac<det left[ A_|dots|A_||A_|dots|A_ right]> quad npu quad kin . $$ Для получения значения $ x_ $ в числитель ставится определитель, получающийся из $ det A_ $ заменой его $ k_ $-го столбца на столбец правых частей ( здесь $ | $ означает конкатенацию).

Доказательство ☞ ЗДЕСЬ

Пример. Решить систему уравнений

$$ left<begin 2x_1& +3x_2&+11x_3&+5x_4 &=& color2,\ x_1& +x_2&+5x_3&+2x_4 &=& color1 ,\ 2x_1& +x_2&+3x_3&+2x_4 &=&color,\ x_1& +x_2&+3x_3&+4x_4 &=&color. endright. $$

Решение. $$ x_1=frac<left|begin color2 & 3&11&5 \ color1 & 1&5&2 \ color& 1&3&2 \ color & 1&3&4 endright|> <left|begin 2& 3&11&5 \ 1& 1&5&2 \ 2& 1&3&2 \ 1& 1&3&4 endright|>=frac=-2, x_2=frac<left|begin 2& color2&11&5 \ 1& color1&5&2 \ 2& color&3&2 \ 1& color&3&4 endright|> <left|begin 2& 3&11&5 \ 1& 1&5&2 \ 2& 1&3&2 \ 1& 1&3&4 endright|>=frac=0, dots $$ Найдите оставшиеся компоненты решения. ♦

Решение системы линейных уравнений с квадратной матрицей $ A_ $ является непрерывной функцией коэффициентов этой системы при условии, что $ det A_ ne 0 $.

Кроме того, формулы Крамера начинают конкурировать по вычислительной эффективности с методом Гаусса в случае систем, зависящих от параметра. Подробнее ☞ ЗДЕСЬ.

Еще один способ решения системы основан на построении обратной матрицы: $$ AX= quad Rightarrow quad X=A^ . $$ Этот способ малоэффективен при фиксированных числовых $ A_ $ и $ _ $.

Найти достаточное условие существования общего решения систем уравнений:

$$ A_1 X = _1 quad u quad A_2 Y = _2 , $$ при квадратных матрицах $ A_1 $ и $ A_2 $ одинакового порядка.

Видео:Система уравнений: метод исключения переменной | Системы уравнений | Алгебра 1Скачать

Теорема Кронекера-Капелли

Матрица, получающаяся конкатенацией матрицы $ A_ $ и столбца правых частей $ _ $ $$ [ A| ] = left( begin a_ & a_ & dots & a_ & b_1 \ a_ & a_ & dots & a_ & b_2 \ dots &&& & dots \ a_ & a_ & dots & a_ & b_m end right)_ $$ называется расширенной матрицей системы линейных уравнений $ AX= $.

Теорема [Кронекер, Капелли]. Система $ AX= $ совместна тогда и только тогда, когда ранг матрицы этой системы совпадает с рангом ее расширенной матрицы:

$$ operatorname, A = operatorname, [ A| ] . $$ При выполнении этого условия, система имеет единственное решение, если число неизвестных $ n_ $ совпадает с общим значением ранга $ mathfrak r_ $, и бесконечное множество решений, если $ n_ $ больше этого значения.

Доказательство необходимости. Пусть существует решение $ x_1=alpha_1,dots,x_n=alpha_n $ системы, тогда $$alpha_1 A_+dots+alpha_n A_= ,$$ т.е. столбец $ $ линейно выражается через столбцы $ A_,dots,A_ $. Но тогда $$ operatorname <A_,dots,A_>=operatorname <A_,dots,A_,> .$$ Следовательно $ operatorname, A = operatorname, [ A| ] $.

Доказательство достаточности проводится в следующем пункте. ♦

Пример. Исследовать совместность системы уравнений

Решение. В этом примере число уравнений совпадает с числом неизвестных. Это обстоятельство несколько облегчает рассуждения. Обратимся к замечанию из предыдущего пункта: система л.у. с числом уравнений, совпадающем с числом неизвестных, как правило, совместна. Тогда попробуем установить условия, обеспечивающие противоположное свойство — несовместность. Оно, фактически, единственно: за все отвечает определитель системы $ det A_ $. Если он отличен от нуля — система совместна. $$det A = left| begin<color> &1&1&1 \ 1&<color>&1&1 \ 1&1&<color>&1 \ 1&1&1&<color> end right|= left| begin (<color>-1) &(1-<color>)&0&0 \ 0&(<color>-1)&(1-<color>)&0 \ 0&0&(<color>-1)&(1-<color>) \ 1&1&1&<color> end right| =(<color>-1)^3 left| begin 1 &-1&0&0 \ 0&1&-1&0 \ 0&0&1&-1 \ 1&1&1&<color> end right|= $$ $ =(<color>-1)^3(<color>+3) $. По теореме Крамера при $ <color>ne 1 $ и при $ <color>ne -3 $ решение системы единственно: $$x_1=x_2=x_3=x_4=1/(<color>+3) .$$

Осталось исследовать критические случаи: $ <color>=1_ $ и $ <color>= -3 $: определитель системы обращается в нуль, но система может оказаться совместной. Придется вычислять ранги, но, к счастью, уже числовых матриц (а не зависящих от параметра, как исходная!). При $ <color>= 1_ $ имеем $$ operatorname left( begin 1 &1&1&1 \ 1&1&1&1 \ 1&1&1&1 \ 1&1&1&1 end right)= operatorname left( begin 1&1&1&1&1 \ 1&1&1&1&1 \ 1&1&1&1&1 \ 1&1&1&1&1 end right)=1 , $$ и система совместна. Она эквивалентна единственному уравнению $$x_1+x_2+x_3+x_4=1 ,$$ которое имеет бесконечно много решений.

При $ <color>= -3 $: $$ operatorname left( begin -3 &1&1&1 \ 1&-3&1&1 \ 1&1&-3&1 \ 1&1&1&-3 end right)=3,quad operatorname left( begin -3 &1&1&1&1 \ 1&-3&1&1&1 \ 1&1&-3&1&1 \ 1&1&1&-3&1 end right)=4 $$ и система несовместна.

Ответ. Система несовместна при $ <color> = -3 $; она имеет бесконечное множество решений при $ <color> = 1_ $ и единственное решение при $ <color> notin $.

Система однородных уравнений

$$ left< begin a_x_1 &+a_x_2&+ ldots&+a_x_n &=0,\ a_x_1 &+a_x_2&+ ldots&+a_x_n &=0,\ dots & & & dots & \ a_x_1 &+a_x_2&+ ldots&+a_x_n &=0 end right. $$ всегда совместна: она имеет тривиальное решение $ x_1=0,dots,x_n=0 $. Для того, чтобы у нее существовало еще и нетривиальное решение необходимо и достаточно, чтобы определитель ее матрицы был равен нулю.

Пример. Найти условие, при котором три точки плоскости с координатами $ (x_1,y_1), (x_2,y_2) $ и $ (x_3,y_) $ лежат на одной прямой.

Решение. Будем искать уравнение прямой в виде $ ax+by+c=0 $ при неопределенных коэффициентах $ a,b,c_ $. Если точки лежат на прямой, то получаем для определения этих коэффициентов систему линейных уравнений: $$ left< begin ax_1+by_1+c & =0\ ax_2+by_2+c & =0\ ax_3+by_3+c & =0 end right. $$ Получившаяся система является однородной, условие существования у нее нетривиального решения (т.е. набора $ (a,b,c)_ $ при хотя бы одном из чисел отличном от нуля): $$ left|begin x_1 & y_1 & 1 \ x_2 & y_2 & 1 \ x_3 & y_3 & 1 end right|=0 . $$ ♦

Доказать, что для совместности системы

$$ left< begin a_x_1+a_x_2+a_x_3 &=& b_1 \ a_x_1+a_x_2+a_x_3 &=& b_2 \ a_x_1+a_x_2+a_x_3 &=& b_3 \ a_x_1+a_x_2+a_x_3 &=& b_4 end right. $$ необходимо, чтобы было выполнено условие $$ left| begin a_&a_& a_ & b_1 \ a_&a_& a_ & b_2 \ a_&a_& a_ & b_3 \ a_&a_& a_ & b_4 end right|=0 quad . $$ Является ли это условие достаточным для совместности?

An elementary treatise on determinants

в следующей формулировке.

Теорема. Для того чтобы система $ n_ $ неоднородных уравнений была совместна, необходимо и достаточно, чтобы порядок наибольшего отличного от нуля минора был одинаков в расширенной и нерасширенной матрице системы.

Додсон — один из самых знаменитых математиков мира. Назовите его псевдоним.

Ответ ☞ ЗДЕСЬ

Видео:12. Метод Гаусса решения систем линейных уравнений. Часть 1.Скачать

Общее решение

Пусть выполнено условие теоремы Кронекера-Капелли: $ operatorname (A)=operatorname[Amid mathcal B ] =mathfrak $. По определению ранга матрицы, в матрице $ A $ существует минор порядка $ mathfrak $, отличный от нуля; этот же минор останется и минором расширенной матрицы $ [ Amid mathcal B ] $. Пусть, для определенности, ненулевой минор находится в левом верхнем углу матрицы 4) : $$ Delta = Aleft( begin 1 & 2 & dots & mathfrak \ 1 & 2 & dots & mathfrak end right) = left| begin a_ & a_ & dots & a_<1mathfrak> \ a_ & a_ & dots & a_<2mathfrak> \ dots &&& dots \ a_<mathfrak1> & a_<mathfrak2> & dots & a_ <mathfrakmathfrak> end right| ne 0 . $$ Тогда первые $ mathfrak $ строк матрицы $ A $ линейно независимы, а остальные будут линейно выражаться через них. Это же утверждение будет справедливо и для строк матрицы $ [Amid mathcal B] $. Умножая первые $ mathfrak $ уравнений системы на соответствующие числа и складывая их, получим любое оставшееся уравнение. Таким образом, система уравнений может быть заменена эквивалентной ей системой из первых $ mathfrak $ уравнений: $$ left< begin a_x_1+dots+a_<1mathfrak>x_<mathfrak>&+a_<1,mathfrak+1>x_<mathfrak+1>+ dots +a_x_n&=&b_1, \ dots & & & dots \ a_<mathfrak1>x_1+dots+a_<mathfrakmathfrak>x_<mathfrak>& +a_<mathfrak,mathfrak+1>x_<mathfrak+1>+dots +a_<mathfrakn>x_n&=&b_mathfrak end right. quad iff quad A^ X=^ $$ Если $ mathfrak=n $, то матрица $ A^ $ квадратная. По предположению $ det A^ ne 0 $. По теореме Крамера решение такой системы единственно.

Пусть теперь $ mathfrak произвольных фиксированных значениях $ x_<mathfrak+1>,dots,x_n $: $$ x_j=frac< left| begin a_ & dots &a_ &left[ b_1-(a_<1,mathfrak+1>x_<mathfrak+1>+dots +a_x_n) right] &a_& dots &a_<1mathfrak> \ dots &&&dots&&& dots \ a_<mathfrak1> & dots &a_<mathfrak,j-1> & left[ b_<mathfrak>- (a_<mathfrak,mathfrak+1>x_<mathfrak+1>+dots +a_<mathfrakn>x_n) right] &a_<mathfrak,j+1>& dots &a_<mathfrakmathfrak> end right| > $$ $$ mbox jin <1,dots, mathfrak> . $$ Таким образом, в этом случае система имеет бесконечное множество решений. Используя свойство линейности определителя по столбцу (см. свойство 5 ☞ ЗДЕСЬ ), формулы можно переписать в виде $$ x_j=beta_j + gamma_<j,mathfrak+1>x_<mathfrak+1>+dots+gamma_x_n npu jin <1,dots, mathfrak> . $$ Здесь $$ beta_j =frac left| begin a_ & dots &a_ & b_1 &a_& dots &a_<1mathfrak> \ vdots &&&vdots&&& vdots \ a_<mathfrak1> & dots &a_<mathfrak,j-1> & b_<mathfrak> &a_<mathfrak,j+1>& dots &a_<mathfrakmathfrak> end right|, , $$ $$ gamma_ = -frac left| begin a_ & dots &a_ & a_ &a_& dots &a_<1mathfrak> \ vdots &&&vdots&&& vdots \ a_<mathfrak1> & dots &a_<mathfrak,j-1> & a_<mathfrakk> &a_<mathfrak,j+1>& dots &a_<mathfrakmathfrak> end right| . $$ Эти формулы называются общим решением системы $ A X=mathcal B $. Участвующие в них переменные $ x_<mathfrak+1>,dots,x_n $ называются основными (или свободными), а $ x_1,dots,x_<mathfrak> $ — зависимыми. Решение, получающееся из общего решения фиксированием значений основных переменных, называется частным решением системы уравнений.

Пример. Исследовать совместность и найти общее решение системы уравнений:

Решение проведем двумя способами, соответствующими двум способам вычисления ранга матрицы. Вычисляем сначала ранг матрицы $ A $ по методу окаймляющих миноров: $$ |2| ne 0,quad left| begin 2 & 1 \ 6 & 2 end right| ne 0, quad left| begin 2 & 1 & 2 \ 6 & 2 & 4 \ 4 & 1 & 1 end right|=2 ne 0 , $$ а все миноры, окаймляющие последний, равны нулю. Итак, $ operatorname (A) =3 $. Для нахождения ранга расширенной матрицы $ [Amid mathcal B] $ достаточно проверить окаймление найденного ненулевого минора третьего порядка с помощью элементов взятых из столбца правых частей. Имеется всего один такой минор, и он равен нулю. Следовательно $ operatorname[ Amid mathcal B ] =3 $, система совместна, и имеет бесконечное множество решений.

Ненулевой минор третьего порядка (базисный минор) находится в первой, второй и четвертых строках, что означает линейную независимость соответствующих уравнений. Третье уравнение линейно зависит от остальных, и может быть отброшено. Далее, указанный базисный минор образован коэффициентами при $ x_1,x_3 $ и $ x_4 $. Следовательно оставшиеся уравнения могут быть разрешены относительно этих переменных, т.е. они — зависимые, а $ x_2 $ и $ x_5 $ — основные. Использование формулы дает общее решение $$ begin x_1&=&frac<left| begin 2 & 1 & 2 \ 3 & 2 & 4 \ 1 & 1 & 1 end right|> -x_2frac<left| begin -1 & 1 & 2 \ -3 & 2 & 4 \ -2 & 1 & 1 end right|> -x_5frac<left| begin 3 & 1 & 2 \ 5 & 2 & 4 \ 2 & 1 & 1 end right|> =-frac+fracx_2+fracx_5, \ & & \ x_3&=&frac<left| begin 2 & 2 & 2 \ 6 & 3 & 4 \ 4 & 1 & 1 end right|> -x_2frac<left| begin 2 & -1 & 2 \ 6 & -3 & 4 \ 4 & -2 & 1 end right|> -x_5frac<left| begin 2 & 3 & 2 \ 6 & 5 & 4 \ 4 & 2 & 1 end right|>=3-4x_5, \ & & \ x_4 &=&frac<left| begin 2 & 1 & 2 \ 6 & 2 & 3 \ 4 & 1 & 1 end right|> -x_2frac<left| begin 2 & 1 & -1 \ 6 & 2 & -3 \ 4 & 1 & -2 end right|> -x_5frac<left| begin 2 & 1 & 3 \ 6 & 2 & 5 \ 4 & 1 & 2 end right|> = 0. end $$ Решим теперь ту же задачу, воспользовавшись методом Гаусса исключения переменных в системе линейных уравнений: $$ left< begin 2x_1&-x_2&+x_3&+2x_4&+3x_5&=&2, \ &&x_3&+2x_4&+4x_5&=&3, \ &&&x_4&&=&0 end right. $$ Используя обратный ход метода Гаусса, снова приходим к полученным формулам.

Ответ. Общее решение системы: $ x_1=1/2 (x_2+x_5-1), x_3=3-4,x_5, x_4=0 $.

Проанализируем теперь полученные общие формулы для общего решения. В этих формулах $ beta_j $ представляет решение системы, получаемое при $ x_<mathfrak+1>=0,dots,x_n=0 $. Величины же коэффициентов $ gamma_ $ вовсе не зависят от правых частей системы и будут одинаковыми при любых значениях $ b_1,dots,b_m $. В частности, если $ b_1=0,dots,b_m=0 $, то в формулах величины $ beta_j $ обращаются в нуль и эти формулы превращаются в $$ x_j=gamma_<j,mathfrak+1>x_<mathfrak+1>+dots+gamma_x_n npu jin <1,dots, mathfrak> . $$

Вывод. Формула общего решения системы $ A X=mathcal B $: $$ x_j=beta_j + gamma_<j,mathfrak+1>x_<mathfrak+1>+dots+gamma_x_n npu jin <1,dots, mathfrak> $$ состоит из двух частей: слагаемые, не содержащие свободных переменных, определяют частное решение неоднородной системы: $$ x_1= beta_1,dots, x_<mathfrak>= beta_<mathfrak>,x_<mathfrak+1>=0,dots,x_n=0 ; $$ оставшиеся после их отбрасывания формулы задают общее решение системы $ AX=mathbb O $. Этот результат обобщается в следующей теореме.

Теорема. Общее решение системы уравнений $ A X=mathcal B $ представимо в виде суммы какого-то частного решения этой системы и общего решения соответствующей однородной системы $ A X=mathbb O $.

Доказательство тривиально если система $ A X=mathcal B $ имеет единственное решение. Если же решений бесконечно много, то выбрав какое-то одно частное $ X=X_1 $ мы получаем, что любое другое частное решение $ X=X_2 $ должно быть связано с первым соотношением $$ A(X_2-X_1)=mathbb O , $$ т.е. разность частных решений неоднородной системы обязательно является решением однородной системы уравнений $ AX=mathbb O $. ♦

Теперь посмотрим как можно описать общее решение однородной системы.

Система однородных уравнений

Система линейных уравнений называется однородной, если все коэффициенты правых частей равны нулю: $$ left< begin a_x_1 &+a_x_2&+ ldots&+a_x_n &=0,\ a_x_1 &+a_x_2&+ ldots&+a_x_n &=0,\ dots & & & dots & \ a_x_1 &+a_x_2&+ ldots&+a_x_n &=0. end right. $$ или, в матричном виде: $$ A_X=_ $$

Задача ставится о поиске нетривиального решения. Оно не всегда существует. Так, к примеру, если матрица $ A_ $ системы — квадратная и имеет ненулевой определитель, то, согласно теореме Крамера, нетривиальных решений у однородной системы нет. Теорема Кронекера-Капелли утверждает, что условие $ det (A_) = 0 $ является и достаточным для существования нетривиального решения.

Теорема 1. Для того, чтобы система однородных уравнений с квадратной матрицей $ A_ $ имела нетривиальное решение необходимо и достаточно, чтобы $ det (A_) = 0 $.

Для произвольной (не обязательно квадратной) матрицы $ A_ $ имеет место следующий общий результат.

Теорема 2. Если $ operatorname (A)=mathfrak r 5) $ A_^ $.

Теорема 3. Множество решений системы однородных уравнений образует линейное подпространство пространства $ mathbb A^ $. Размерность этого подпространства равна $ n-mathfrak r $, а фундаментальная система решений образует его базис.

Пусть матрица системы $ AX=mathbb O $ квадратная и

$$ operatorname (A) =n_-1 , .$$ Доказать, что если ненулевой минор матрицы порядка $ n_-1 $ соответствует какому-нибудь элементу $ j_ $-й строки, то система алгебраических дополнений к элементам $ a_,dots,a_^ $ этой строки составляет ФСР для $ AX=mathbb O_ $. Например, для системы $$ left< begin a_x_1 +a_x_2+a_x_3&=0,\ a_x_1 +a_x_2+a_x_3&=0 end right. $$ ФСР состоит из решения $$ x_1=left| begin a_ & a_ \ a_ & a_ end right| , x_2=-left| begin a_ & a_ \ a_ & a_ end right| , x_3=left| begin a_ & a_ \ a_ & a_ end right| , $$ если только хотя бы один из миноров отличен от нуля.

Теперь обсудим способы нахождения ФСР.

1. Первый из них получается из общего метода решения системы линейных уравнений, рассмотренного в предыдущем пункте. Так же, как и в том пункте, сделаем упрощающее обозначения предположение, что зависимыми переменными являются первые $ x_,dots,x_ $, т.е. общее решение задается формулами $$ x_j=gamma_<j,mathfrak+1>x_<mathfrak+1>+dots+gamma_x_n npu jin <1,dots, mathfrak> . $$ Иными словами, вектор столбец $$ X=left(begin gamma_<1,mathfrak+1>x_<mathfrak+1>+dots+gamma_x_n \ gamma_<2,mathfrak+1>x_<mathfrak+1>+dots+gamma_x_n \ vdots \ gamma_<mathfrak,mathfrak+1>x_<mathfrak+1>+dots+gamma_<mathfrakn>x_n \ x_<mathfrak+1> \ x_<mathfrak+2> \ vdots \ x_ endright) $$ будет решением однородной системы при любых наборах значений основных переменных $ x_<mathfrak+1>,dots,x_ $. Представим этот вектор в виде суммы векторов: $$ =x_<mathfrak+1> underbrace< left(begin gamma_<1,mathfrak+1> \ gamma_<2,mathfrak+1> \ vdots \ gamma_<mathfrak,mathfrak+1> \ 1 \ 0 \ vdots \ 0 endright)>_ + x_<mathfrak+2> underbrace<left(begin gamma_<1,mathfrak+2> \ gamma_<2,mathfrak+2> \ vdots \ gamma_<mathfrak,mathfrak+2> \ 0 \ 1 \ vdots \ 0 endright)>_+dots+ x_ underbrace<left(begin gamma_ \ gamma_ \ vdots \ gamma_<mathfrakn> \ 0 \ 0 \ vdots \ 1 endright)>_<X_> . $$ Таким образом, любое решение однородной системы представимо в виде линейной комбинации $ n_- mathfrak r $ фиксированных решений. Именно эти решения и можно взять в качестве ФСР — их линейная независимость очевидна (единицы в нижних частях каждого вектора $ X_ $ расположены на разных местах, и ни какая линейная комбинация столбцов $ < X_1,dots,X_> $ не сможет обратить их одновременно в нуль).

Оформим этот способ построения ФСР в теорему:

Теорема 4. Если система уравнений $ AX=mathbb O $ имеет структуру матрицы $ A_ $ вида:

$$ A = left[ E_ mid P_ right] , $$ то ее ФСР состоит из столбцов матрицы $$ left[ begin — P^ \ hline E_ end right] . $$

Пример. Найти ФСР для системы уравнений

Решение. Приводим систему к трапециевидному виду: $$ left< begin x_1-&x_2+&x_3-&x_4=&0, \ &&x_3+&4x_4=&0 end right. $$ В качестве зависимых переменных можно взять, например, $ x_ $ и $ x_ $. $$ begin x_1 & x_3 & x_2 & x_4 \ hline 1 & 0 & 1 & 0 \ 5 & -4 & 0 & 1 end $$

2. Этот способ напоминает вычисление обратной матрицы методом приписывания единичной матрицы. Транспонируем матрицу $ A_ $ системы и припишем к ней справа единичную матрицу порядка $ n_ $: $$ left[ A^ | E_n right] = left(begin a_ & a_ & dots & a_ & 1 & 0 & 0 & dots & 0 \ a_ & a_ & dots & a_ & 0 & 1 & 0 & dots & 0 \ a_ & a_ & dots & a_ & 0 & 0 & 1 & dots & 0 \ vdots & & & vdots & vdots & & & ddots & vdots \ a_ & a_ & dots & a_ & 0 & 0 & 0 & dots & 1 end right) ; $$ здесь $ |_ $ означает конкатенацию. Получившуюся матрицу элементарными преобразованиями строк приводим к форме: $$ left( begin hat A & K \ mathbb O & L end right) = left(begin color & * & * & dots & * & * & * & * & * & * & * & dots & * \ 0 & color & * & dots & * & * & * & * & * & * & * & dots & * \ 0 & 0 & color & dots & * & * & * & * & * & * & * & dots & * \ vdots & & & ddots & & vdots & & & vdots & & & & vdots \ 0 & 0 & dots & & 0 & color & * & * & * & * & * & dots & * \ hline 0 & 0 & dots & 0 & 0 & 0 & 0 & 0 & Box & Box & Box & dots & Box \ vdots & & & & & vdots & & & vdots & & & & vdots \ 0 & 0 & dots & 0 & 0 & 0 & 0 & 0 & Box & Box & Box & dots & Box end right) begin left.begin \ \ \ \ \ endright> mathfrak r \ left. begin \ \ \ endright> n — mathfrak r end . $$ Элементы трапециевидной матрицы $ hat A $, обозначенные $ color $, могут быть равны нулю, но $ operatorname(hat A)= mathfrak r_ $. В этом случае строки матрицы $ L_ $, образовавшейся в правом нижнем углу (ее элементы обозначены $ Box $), составляют ФСР для системы $ AX=mathbb O $.

Пример. Найти ФСР для системы уравнений

$$ left< begin x_1 &+2,x_2&+ x_3&+3,x_4&-x_5&+2,x_6=&0,\ -3x_1 &-x_2&+ 2,x_3&-4,x_4&+x_5&-x_6=&0,\ x_1 &+x_2&+ 3,x_3&+2,x_4&+x_5&+3,x_6=&0,\ -8,x_1 &-7,x_2&+ 4,x_3&-15,x_4&+6,x_5&-5,x_6=&0,\ 6x_1 &+5,x_2& +5,x_3&+11,x_4 &&+9,x_6=&0. end right. $$ Решение. Преобразуем матрицу $ left[ A^ | E_6 right] $

$$ left(begin 1 & -3 & 1 & -8 & 6 & 1 \ 2 & -1 & 1 & -7 & 5 & & 1 \ 1 & 2 & 3 & 4 & 5 & & & 1 \ 3 & -4 & 2 & -15 & 11 &&&& 1 \ -1 & 1 & 1 & 6 & 0 &&&&& 1 \ 2 & -1 & 3 & -5 & 9 &&&&&& 1 end right)_ $$ к трапециевидной форме с помощью элементарных преобразований строк: $$ rightarrow left(begin 1 & -3 & 1 & -8 & 6 & 1 \ 0 & 5 & -1 & 9 & -7 &-2 & 1 \ 0 & 5 & 2 & 12 & -1 &-1 &0 & 1 \ 0 & 5 & -1 & 9 & -7 &-3&0&0& 1 \ 0 & -2 & 2 & -2 & 6 &1&0&0&0& 1 \ 0 & 5 & 1 & 11 & -3 &-2&0&0&0&0& 1 end right)rightarrow $$ $$ rightarrow left(begin 1 & -3 & 1 & -8 & 6 & 1 \ 0 & 5 & -1 & 9 & -7 &-2 & 1 \ 0 & 0 & 3 & 3 & 6 &1 &-1 & 1 \ 0 & 0 & 0 & 0 & 0 &-1&-1&0& 1 \ 0 & 0 & 8/5 & 8/5 & 16/5 &1/5&2/5&0&0& 1 \ 0 & 0 & 2 & 2 & 4 &0&-1&0&0&0& 1 end right)rightarrow $$ $$ rightarrow left(begin 1 & -3 & 1 & -8 & 6 & 1 \ 0 & 5 & -1 & 9 & -7 &-2 & 1 \ 0 & 0 & 3 & 3 & 6 &1 &-1 & 1 \ 0 & 0 & 0 & 0 & 0 &-1&-1&0& 1 \ 0 & 0 & 0 & 0 & 0 &-1/3&14/15&-8/15&0& 1 \ 0 & 0 & 0 & 0 & 0 &-2/3&-1/3&-2/3&0& 0 & 1 end right) $$

3. Еще один способ построения ФСР основан на теореме Гамильтона-Кэли.

Теорема. Пусть матрица системы $ AX=mathbb O $ квадратная и $ operatorname (A) = $. Тогда характеристический полином матрицы $ A_ $ имеет вид:

Пример. Найти ФСР для системы уравнений

Решение. Здесь $$ A= left( begin 1 & 1 & -1 & -1 \ 2 & 3 & 1 & -2 \ 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 0 end right), quad det (A-lambda E) = lambda^2(lambda^2-4lambda+1), $$ $$ A^2-4A+E= left( begin 0 & 0 & 4 & 1 \ 0 & 0 & -3 & 0 \ 0 & 0 & 1 & 0 \ 0 & 0 & 0 & 1 end right) $$

Блок-схемы зависимости множества решений системы уравнений $ AX= mathcal B $ от комбинации чисел $ n, mathfrak r $ ☞ ЗДЕСЬ.

Видео:Матричный метод решения систем уравненийСкачать

Геометрическая интерпретация

Геометрический смысл введенных определений поясним на примере $ mathbb R^ $. Уравнение $$ a_1x_1+a_2x_2+a_3x_3=b $$ — при фиксированных вещественных коэффициентах $ a_1,a_2,a_3 $ (хотя бы один из них считаем отличным от нуля) и $ b_ $ — задает плоскость. Если, к примеру, $ a_1ne 0 $, то из уравнения получаем выражение для $ x_ $ как функции $ x_2,x_3 $: $$ x_1=frac-fracx_2-fracx_3 . $$ В этом представлении переменные $ x_ $ и $ x_ $ могут принимать любые вещественные значения независимо друг от друга, а вот переменная $ x_ $ полностью определяется заданием $ x_ $ и $ x_ $. С одной стороны, последняя формула определяет общее решения системы линейных уравнений (которая в нашем частном случае состоит из одного-единственного уравнения); переменные $ x_ $ и $ x_ $ выбраны основными, а $ x_ $ оказывается зависимой. Строго говоря, координаты любой точки плоскости можно представить формулами $$x_1=frac-fract-fracu, x_2=t, x_3=u quad npu quad subset mathbb R , $$ которые называются параметрическим представлением плоскости. Таким образом, получили геометрическую интерпретацию общего решения системы уравнений. Идем далее: представим последние формулы в векторной форме: $$ left( begin x_1 \ x_2 \ x_3 end right)= left( begin b/a_1- t, a_2/a_1- u, a_3/a_1 \ t \ u end right)= left( begin b/a_1\ 0 \ 0 end right)+ t left( begin -a_2/a_1\ 1 \ 0 end right) + u left( begin -a_3/a_1\ 0 \ 1 end right) . $$ Какой геометрический смысл имеет каждое из слагаемых? Первое слагаемое $$ X_0=left( begin b/a_1\ 0 \ 0 end right) $$ получается при задании $ t=0,u=0_ $ в общем решении. Это — частное решение нашего уравнения и определяет точку, через которую проходит плоскость. Два оставшихся столбца $$ X_1=left( begin -a_2/a_1\ 1 \ 0 end right) quad u quad X_2=left( begin -a_3/a_1\ 0 \ 1 end right) $$ не задают решения нашего уравнения — если только $ bne 0_ $. Но оба удовлетворяют однородному уравнению $$ a_1x_1+a_2x_2+a_3x_3=0 , $$ Последнее также определяет плоскость — параллельную исходной и проходящую через начало координат. Первая плоскость получается из второй сдвигом (параллельным переносом) на вектор $ vec $: и этот факт составляет геометрическую интерпретацию теоремы, сформулированной в конце ☞ ПУНКТА:

Теорема. Общее решение системы уравнений $ A X=mathcal B $ представимо в виде суммы какого-то частного решения этой системы и общего решения соответствующей однородной системы $ A X=mathbb O $.

Координаты произвольной точки плоскости $ a_1x_1+a_2x_2+a_3x_3=0 $ задаются соотношениями $$ left( begin x_1 \ x_2 \ x_3 end right)=tX_1+uX_2 . $$ Векторы пространства $ vec $ и $ vec $ являются базисными векторами плоскости — любой вектор $ vec $, лежащий в плоскости, через них выражается и они линейно независимы. Но $ X_ $ и $ X_ $ определяют фундаментальную систему решений однородного уравнения. Таким образом, мы получили геометрическую интерпретацию для ФСР: она задает базисные векторы плоскости, проходящей через начало координат.

Теперь рассмотрим систему из двух уравнений: $$ left<begin a_x_1 +a_x_2+a_x_3 &=&b_1,\ a_x_1 +a_x_2+a_x_3 &=&b_2. endright. $$ Ее можно интерпретировать как пересечение двух плоскостей в $ mathbb R^ $. Здесь уже возможны варианты: пересечение может оказаться как пустым так и непустым. От чего это зависит? — В соответствии с теоремой Кронекера-Капелли, надо сравнить два числа $$ operatorname left( begin a_ & a_ & a_ \ a_ & a_ & a_ end right) quad u quad operatorname left( begin a_ & a_ & a_ & b_1 \ a_ & a_ & a_ & b_2 end right) . $$ Очевидно, ни одно из них не может быть большим $ 2_ $. Если оба равны $ 2_ $ и этот факт обеспечен, например, условием $$ left| begin a_ & a_ \ a_ & a_ end right| ne 0, $$ то решения системы определяют прямую в пространстве. Действительно, при таком условии систему можно разрешить относительно неизвестных $ x_ $ и $ x_ $ и представить общее решение в виде: $$ x_1= frac<left|begin b_1 & a_ \ b_2 & a_ end right|><left|begin a_ & a_ \ a_ & a_ end right|>+ frac<left|begin a_ & a_ \ a_ & a_ end right|><left|begin a_ & a_ \ a_ & a_ end right|>x_3 , quad x_2= frac<left|begin a_ & b_ \ a_ & b_ end right|><left|begin a_ & a_ \ a_ & a_ end right|>- frac<left|begin a_ & a_ \ a_ & a_ end right|><left|begin a_ & a_ \ a_ & a_ end right|>x_3 . $$ В этих формулах переменная $ x_ $ принимает любое значение, а значения переменных $ x_ $ и $ x_ $ линейно выражаются через $ x_ $. Общее решение фактически задает прямую в параметрическом виде: координаты произвольной ее точки определяются формулами $$ left( begin x_1 \ x_2 \ x_3 end right)=X_0+tX_1 , $$ где вектор $$ quad X_0 = left(frac<left|begin a_ & b_ \ a_ & b_ end right|><left|begin a_ & a_ \ a_ & a_ end right|> , frac<left|begin a_ & b_ \ a_ & b_ end right|><left|begin a_ & a_ \ a_ & a_ end right|>, 0right)^ $$ задает координаты точки, лежащей на прямой (т.е. принадлежащей пересечению плоскостей), а вектор $$ X_1= left(frac<left|begin a_ & a_ \ a_ & a_ end right|><left|begin a_ & a_ \ a_ & a_ end right|>, — frac<left|begin a_ & a_ \ a_ & a_ end right|><left|begin a_ & a_ \ a_ & a_ end right|>, 1 right)^ $$ является направляющим для прямой. С тем же успехом мы могли бы взять в качестве направляющего вектор, получающийся растяжением $ X_ $: $$ tilde X_1 = left(left|begin a_ & a_ \ a_ & a_ end right|, — left|begin a_ & a_ \ a_ & a_ end right|, left|begin a_ & a_ \ a_ & a_ end right| right)^ . $$ Очевидно, что любой из векторов $ X_ $ или $ tilde X_1 $ задает фундаментальную систему решений однородной системы уравнений 10) $$ left<begin a_x_1 +a_x_2+a_x_3 &=&0,\ a_x_1 +a_x_2+a_x_3 &=&0. endright. $$ Последняя определяет прямую в $ mathbb R^3 $, проходящую через начало координат. Мы снова получаем интерпретацию теоремы: общее решение неоднородной системы получается сдвигом (параллельным переносом) общего решения однородной системы на вектор $ vec $.

Мы рассмотрели пока только случай пересекающихся плоскостей в пространстве. Его можно считать общим, т.е. случаем «как правило»: две случайным образом выбранные плоскости в $ mathbb R^ $ пересекаться будут. Исследуем теперь исключительный случай — параллельности плоскостей. Исключительность этого случая может быть проверена и аналитикой. Для несовместности системы из двух уравнений необходимо, чтобы ранг ее матрицы $$ left( begin a_ & a_ & a_ \ a_ & a_ & a_ end right) $$ оказался меньшим $ 2_ $. Это равносильно тому, что все миноры второго порядка этой матрицы обращаются в нуль: $$ left| begin a_ & a_ \ a_ & a_ end right|=0, left| begin a_ & a_ \ a_ & a_ end right| =0, left| begin a_ & a_ \ a_ & a_ end right|=0 . $$ Эти условия можно переписать в виде $$ frac<a_><a_>=frac<a_><a_>=frac<a_><a_> ; $$ и, если обозначить общую величину последний отношений через $ tau_ $, то получаем: $$ (a_,a_,a_)=tau (a_,a_,a_) . $$ Если вспомнить, что каждый из этих наборов коэффициентов задает вектор $ vec<OA^> $ в $ mathbb R^ $, перпендикулярный соответствующей плоскости, то, в самом деле, плоскости, определяемые уравнениями, оказываются параллельными. Пересекаться они, как правило, не будут: для пересечения необходимо, чтобы расширенная матрица системы $$ left( begin a_ & a_ & a_ & b_1 \ a_ & a_ & a_ & b_2 end right) $$ имела ранг меньший $ 2_ $. Это возможно только при условии когда коэффициенты правых частей удовлетворяют соотношению $$ b_1 = tau b_2 $$ при величине $ tau_ $ определенной выше. При выполнении этого условия второе уравнение получается из первого домножением на $ tau_ $ и соответствующие плоскости попросту совпадают.

Перейдем теперь к системе из трех уравнений: $$ left< begin a_x_1 +&a_x_2+&a_x_3=&b_1, \ a_x_1 +&a_x_2+&a_x_3=&b_2, \ a_x_1 +&a_x_2+&a_x_3=&b_3. end right. $$ Вариантов взаимного расположения трех плоскостей в $ mathbb R^ $ уже значительно больше. Какой из них будет самым распространенным, то есть случаем «как правило»? Геометрически ответ очевиден: если пересечение двух плоскостей определяет, как правило, прямую, то эта прямая пересекается с третьей плоскостью, как правило, в одной-единственной точке. И алгебра подтверждает геометрию: в комментарии к теореме Крамера говорится, что система, число уравнений которой совпадает с числом неизвестных, как правило, имеет единственное решение. Условие для этого случая «как правило» дается той же теоремой Крамера: $$ left| begin a_ & a_ & a_\ a_ & a_ & a_ \ a_ & a_ & a_ end right| ne 0 . $$

Теорема Кронекера-Капелли в этом случае не нужна — нет, она остается справедливой! — но проверка условия на ранги матриц тривиальна: они оба равны $ 3_ $. Если же указанный определитель обращается в нуль, то этот факт эквивалентен тому, что три строки определителя линейно зависимы. Например, возможно, что строка $ (a_,a_, a_) $ может быть представлена в виде линейной комбинации первых двух строк. Вспомним геометрический смысл этих строк: они задают координаты векторов, перпендикулярных соответствующим плоскостям. Если система уравнений $$ left<begin a_x_1 +a_x_2+a_x_3 &=&b_1,\ a_x_1 +a_x_2+a_x_3 &=&b_2 endright. $$ определяет прямую в $ mathbb R^ $, то оба вектора $ vec<OA^> $ и $ vec<OA^> $ при $ A^= (a_,a_, a_) $ и $ A^= (a_,a_, a_) $ перпендикулярны этой прямой; любая их комбинация также перпендикулярна этой прямой, а, следовательно, плоскость $$ a_x_1 +a_x_2+a_x_3 =b_3 $$ будет ей параллельна.

Статья не закончена!

Видео:Метод Гаусса и метод Жордана-ГауссаСкачать

Ортогональность

Геометрические соображения из предыдущего пункта могут быть обобщены на случай когда размерности рассматриваемых пространств увеличиваются, и мы говорим о точках и векторах многомерных пространств. В последующих пунктах нам потребуются понятия линейной оболочки, линейного пространства, размерности, базиса и координат применительно к векторам-столбцам или векторам-строкам. Их можно найти ☞ ЗДЕСЬ.

Задача решения системы линейных уравнений $$ left< begin 3x_1&+4x_2&-x_3&=2, \ x_1&-2x_2&+3x_3&=1 end right. $$ может быть рассмотрена с двух точек зрения. С одной стороны, переписав систему в виде $$ x_1left(begin 3 \ 1 end right)+ x_2left(begin 4 \ -2 end right)+ x_3left(begin -1 \ 3 end right)= left(begin 2 \ 1 end right) , $$ можно говорить о поиске линейной комбинации столбцов $$ left(begin 3 \ 1 end right), left(begin 4 \ -2 end right), left(begin -1 \ 3 end right) $$ равной заданному столбцу $$ left(begin 2 \ 1 end right) . $$ В случае произвольной системы, записанной в матричном виде $$ A_X=mathcal B_ $$ совместность системы интерпретировать в смысле принадлежности столбца $ mathcal B $ линейной оболочке столбцов $ A_,dots,A_ $: $$ mathcal B=x_1 A_+dots+x_nA_ quad iff quad mathcal B in mathcal L (A_,dots,A_) . $$ В случае положительного ответа числа $ x_,dots,x_n $ интерпретируются как координаты столбца $ mathcal B $ в системе столбцов 11) $ <A_,dots,A_> $.

С другой стороны, к той же задаче решения системы уравнений, в предыдущем ПУНКТЕ мы подошли с другой стороны. Первое из уравнений системы $$ 3,x_1+4,x_2-x_3=2 $$ можно интерпретировать так: скалярное произведение векторов $ vec<^> $ и $ vec<> $ равно фиксированному числу $ 2_ $. Здесь вектора рассматриваются в пространстве строк $ mathbb R_^ $; считается, что каждый вектор имеет начало в начале координат $ mathbf O=[0,0,0] $, а конец — в точке с координатами $ [3,4,-1] $ или, соответственно, $ [x_1,x_2,x_3] $. Если скалярное произведение векторов обозначать скобками $ langle mbox rangle $, то систему уравнений можно переписать в виде $$ langle vec<^> , vec<> rangle=2, langle vec<^> , vec<> rangle=1 quad npu quad A^ = [3,4,-1], A^=[1,-2,3] $$ — строках матрицы $ A_ $. И задачу решения такой системы понимать в смысле: найти координаты всех векторов-строк $ [x_1,x_2,x_3] $ которые обеспечат нам заданные значения скалярных произведений с двумя фиксированными векторами.

Геометрическая интерпретация еще более упрощается если рассмотреть случай однородной системы уравнений. Так, решить систему уравнений $$ left< begin 3x_1&+4x_2&-x_3&=0, \ x_1&-2x_2&+3x_3&=0 end right. $$ означает подобрать вектор $ vec<> $ перпендикулярный (ортогональный) одновременно обоим векторам $ vec<^> $ и $ vec<^> $. Очевидно, что таких векторов в $ mathbb R^ $ бесконечно много — найдя хотя бы один такой вектор $ vec<> $, другие получим его растяжением: $ alpha cdot vec<> $ остается перпендикулярным векторам $ vec<^> $ и $ vec<^> $ при $ forall alpha in mathbb R $.

Все эти геометрические соображения обобщаются в произвольное пространство $ mathbb R_^ $ строк или столбцов, состоящих из $ n_ $ вещественных чисел (компонент). Для этого приходится обобщать понятие скалярного произведения. В общем случае оно вводится аксиоматически (и, более того, в одном и том же множестве может быть определено разными способами, см. ☞ ЕВКЛИДОВО ПРОСТРАНСТВО ). Мы сейчас не будем залезать так глубоко в эту аксиоматику, а просто определим скалярное произведение двух строк $ X=[x_1,x_2,dots,x_n] $ и $ Y=[y_1,y_2,dots,y_n] $ формулой $$ langle X,Y rangle=x_1y_1+x_2y_2+dots+x_ny_n $$ и продекларируем без обоснований, что все привычные нам по случаям $ mathbb R^ $ и $ mathbb R^ $ свойства скалярного произведения будут выполнены.

В терминах скалярного произведения, задачу решения системы линейных уравнений можно переформулировать как поиск строки $ X=[x_1,x_2,dots,x_n] $, ортогональной всем строкам матрицы $ A_ $: $$ langle A^,X rangle=0, langle A^,X rangle=0,dots, langle A^,X rangle=0 . $$ Множество таких строк образует линейное подпространство пространства $ mathbb R_^ $, это подпространство является ортогональным дополнением линейной оболочки $ mathcal L ( A^, A^,dots, A^ ) $ в пространстве $ mathbb R_^ $. Это подпространство называется нуль-пространством матрицы или ядром матрицы $ A_ $ и обозначается 12) $ er (A) $. Фундаментальная система решений системы $ AX=mathbb O $ составляет базис этого подпространства. Для произвольного линейного пространства количество векторов его базиса называется размерностью пространства и обозначается $ operatorname $. Во введенных обозначениях теорема из ☞ ПУНКТА переформулируется так:

Теорема. $ operatorname left( er (A) right)=n- mathfrak r $, где $ n_ $ — количество столбцов матрицы $ A_ $, а $ mathfrak r=operatorname (A) $ — ее ранг.

Видео:9 класс, 11 урок, Методы решения систем уравненийСкачать

Метода Гаусса: примеры решения СЛАУ

В данной статье мы:

• дадим определение методу Гаусса,
• разберем алгоритм действий при решении линейных уравнений, где количество уравнений совпадает c количеством неизвестных переменных, а определитель не равен нулю;
• разберем алгоритм действий при решении СЛАУ с прямоугольной или вырожденной матрицей.

Видео:Метод Гаусса и метод Жордана-Гаусса ➜ 2 метода за 7 минутСкачать

Метод Гаусса — что это такое?

Метод Гаусса — это метод, который применяется при решении систем линейных алгебраических уравнений и имеет следующие преимущества:

• отсутствует необходимость проверять систему уравнений на совместность;
• есть возможность решать системы уравнений, где:
• количество определителей совпадает с количеством неизвестных переменных;
• количество определителей не совпадает с количеством неизвестных переменных;
• определитель равен нулю.
• результат выдается при сравнительно небольшом количестве вычислительных операций.

Видео:Способы решения систем нелинейных уравнений. Практическая часть. 9 класс.Скачать

Основные определения и обозначения

Есть система из р линейных уравнений с n неизвестными ( p может быть равно n ):

a 11 x 1 + a 12 x 2 + . . . + a 1 n x n = b 1 a 21 x 1 + a 22 x 2 + . . . + a 2 n x n = b 2 ⋯ a p 1 x 1 + a p 2 x 2 + . . . + a p n x n = b p ,

где x 1 , x 2 , . . . . , x n — неизвестные переменные, a i j , i = 1 , 2 . . . , p , j = 1 , 2 . . . , n — числа (действительные или комплексные), b 1 , b 2 , . . . , b n — свободные члены.

Если b 1 = b 2 = . . . = b n = 0 , то такую систему линейных уравнений называют однородной, если наоборот — неоднородной.

Решение СЛАУ — совокупность значения неизвестных переменных x 1 = a 1 , x 2 = a 2 , . . . , x n = a n , при которых все уравнения системы становятся тождественными друг другу.

Совместная СЛАУ — система, для которой существует хотя бы один вариант решения. В противном случае она называется несовместной.

Определенная СЛАУ — это такая система, которая имеет единственное решение. В случае, если решений больше одного, то такая система будет называться неопределенной.

Координатный вид записи:

a 11 x 1 + a 12 x 2 + . . . + a 1 n x n = b 1 a 21 x 1 + a 22 x 2 + . . . + a 2 n x n = b 2 ⋯ a p 1 x 1 + a p 2 x 2 + . . . + a p n x n = b p

Матричный вид записи: A X = B , где

A = a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋯ ⋯ ⋯ ⋯ a p 1 a p 2 ⋯ a p n — основная матрица СЛАУ;

X = x 1 x 2 ⋮ x n — матрица-столбец неизвестных переменных;

B = b 1 b 2 ⋮ b n — матрица свободных членов.

Расширенная матрица — матрица, которая получается при добавлении в качестве ( n + 1 ) столбца матрицу-столбец свободных членов и имеет обозначение Т .

T = a 11 a 12 ⋮ a 1 n b 1 a 21 a 22 ⋮ a 2 n b 2 ⋮ ⋮ ⋮ ⋮ ⋮ a p 1 a p 2 ⋮ a p n b n

Вырожденная квадратная матрица А — матрица, определитель которой равняется нулю. Если определитель не равен нулю, то такая матрица, а потом называется невырожденной.

Видео:Система линейных уравнений. Общее решение. Метод ГауссаСкачать

Описание алгоритма использования метода Гаусса для решения СЛАУ с равным количеством уравнений и неизвестных (обратный и прямой ход метода Гаусса)

Для начала разберемся с определениями прямого и обратного ходов метода Гаусса.

Прямой ход Гаусса — процесс последовательного исключения неизвестных.

Обратный ход Гаусса — процесс последовательного нахождения неизвестных от последнего уравнения к первому.

Алгоритм метода Гаусса:

Решаем систему из n линейных уравнений с n неизвестными переменными:

a 11 x 1 + a 12 x 2 + a 13 x 3 + . . . + a 1 n x n = b 1 a 21 x 1 + a 22 x 2 + a 23 x 3 + . . . + a 2 n x n = b 2 a 31 x 1 + a 32 x 2 + a 33 x 3 + . . . + a 3 n x n = b 3 ⋯ a n 1 x 1 + a n 2 x 2 + a n 3 x 3 + . . . + a n n x n = b n

Определитель матрицы не равен нулю.

1. a 11 не равен нулю — всегда можно добиться этого перестановкой уравнений системы;
2. исключаем переменную x 1 из всех уравнений систему, начиная со второго;
3. прибавим ко второму уравнению системы первое, которое умножено на — a 21 a 11 , прибавим к третьему уравнению первое умноженное на — a 21 a 11 и т.д.

После проведенных действий матрица примет вид:

a 11 x 1 + a 12 x 2 + a 13 x 3 + . . . + a 1 n x n = b 1 a ( 1 ) 22 x 2 + a ( 1 ) 23 x 3 + . . . + a ( 1 ) 2 n x n = b ( 1 ) 2 a ( 1 ) 32 x 2 + a ( 1 ) 33 x 3 + . . . + a ( 1 ) 3 n x n = b ( 1 ) 3 ⋯ a ( 1 ) n 2 x 2 + a ( 1 ) n 3 x 3 + . . . + a ( 1 ) n n x n = b ( 1 ) n ,

где a i j ( 1 ) = a i j + a 1 j ( — a i 1 a 11 ) , i = 2 , 3 , . . . , n , j = 2 , 3 , . . . , n , b i ( 1 ) = b i + b 1 ( — a i 1 a 11 ) , i = 2 , 3 , . . . , n .

Далее производим аналогичные действия с выделенной частью системы:

a 11 x 1 + a 12 x 2 + a 13 x 3 + . . . + a 1 n x n = b 1 a ( 1 ) 22 x 2 + a ( 1 ) 23 x 3 + . . . + a ( 1 ) 2 n x n = b ( 1 ) 2 a ( 1 ) 32 x 2 + a ( 1 ) 33 x 3 + . . . + a ( 1 ) 3 n x n = b ( 1 ) 3 ⋯ a ( 1 ) n 2 x 2 + a ( 1 ) n 3 x 3 + . . . + a ( 1 ) n n x n = b ( 1 ) n

Считается, что a 22 ( 1 ) не равна нулю. Таким образом, приступаем к исключению неизвестной переменной x 2 из всех уравнений, начиная с третьего:

• к третьему уравнению систему прибавляем второе, которое умножено на — a ( 1 ) 42 a ( 1 ) 22 ;
• к четвертому прибавляем второе, которое умножено на — a ( 1 ) 42 a ( 1 ) 22 и т.д.

После таких манипуляций СЛАУ имеет следующий вид:

a 11 x 1 + a 12 x 2 + a 13 x 3 + . . . + a 1 n x n = b 1 a ( 1 ) 22 x 2 + a ( 1 ) 23 x 3 + . . . + a ( 1 ) 2 n x n = b ( 1 ) 2 a ( 2 ) 33 x 3 + . . . + a ( 2 ) 3 n x n = b ( 2 ) 3 ⋯ a ( 2 ) n 3 x 3 + . . . + a ( 2 ) n n x n = b ( 2 ) n ,

где a i j ( 2 ) = a ( 1 ) i j + a 2 j ( — a ( 1 ) i 2 a ( 1 ) 22 ) , i = 3 , 4 , . . . , n , j = 3 , 4 , . . . , n , b i ( 2 ) = b ( 1 ) i + b ( 1 ) 2 ( — a ( 1 ) i 2 a ( 1 ) 22 ) , i = 3 , 4 , . . . , n . .

Таким образом, переменная x 2 исключена из всех уравнений, начиная с третьего.

Далее приступаем к исключению неизвестной x 3 , действуя по аналоги с предыдущим образцом:

a 11 x 1 + a 12 x 2 + a 13 x 3 + . . . + a 1 n x n = b 1 a ( 1 ) 22 x 2 + a ( 1 ) 23 x 3 + . . . + a ( 1 ) 2 n x n = b ( 1 ) 2 a ( 2 ) 33 x 3 + . . . + a ( 2 ) 3 n x n = b ( 2 ) 3 ⋯ a ( n — 1 ) n n x n = b ( n — 1 ) n

После того как система приняла такой вид, можно начать обратный ход метода Гаусса:

• вычисляем x n из последнего уравнения как x n = b n ( n — 1 ) a n n ( n — 1 ) ;
• с помощью полученного x n находим x n — 1 из предпоследнего уравнения и т.д., находим x 1 из первого уравнения.

Найти решение системы уравнений методом Гаусса:

3 x 1 + 2 x 2 + x 3 + x 4 = — 2 x 1 — x 2 + 4 x 3 — x 4 = — 1 — 2 x 1 — 2 x 2 — 3 x 3 + x 4 = 9 x 1 + 5 x 2 — x 3 + 2 x 4 = 4

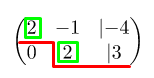
Коэффициент a 11 отличен от нуля, поэтому приступаем к прямому ходу решения, т.е. к исключению переменной x 11 из всех уравнений системы, кроме первого. Для того, чтобы это сделать, прибавляем к левой и правой частям 2-го, 3-го и 4-го уравнений левую и правую часть первого, которая умножена на — a 21 a 11 :

— 1 3 , — а 31 а 11 = — — 2 3 = 2 3 и — а 41 а 11 = — 1 3 .

3 x 1 + 2 x 2 + x 3 + x 4 = — 2 x 1 — x 2 + 4 x 3 — x 4 = — 1 — 2 x 1 — 2 x 2 — 3 x 3 + x 4 = 9 x 1 + 5 x 2 — x 3 + 2 x 4 = 4 ⇔

⇔ 3 x 1 + 2 x 2 + x 3 + x 4 = — 2 x 1 — x 2 + 4 x 3 — x 4 + ( — 1 3 ) ( 3 x 1 + 2 x 2 + x 3 + x 4 ) = — 1 + ( — 1 3 ) ( — 2 ) — 2 x 1 — 2 x 2 — 3 x 3 + x 4 + 2 3 ( 3 x 1 + 2 x 2 + x 3 + x 4 ) = 9 + 2 3 ( — 2 ) x 1 + 5 x 2 — x 3 + 2 x 4 + ( — 1 3 ) ( 3 x 1 + 2 x 2 + x 3 + x 4 ) = 4 + ( — 1 3 ) ( — 2 ) ⇔

⇔ 3 x 1 + 2 x 2 + x 3 + x 4 = — 2 — 5 3 x 2 + 11 3 x 3 — 4 3 x 4 = — 1 3 — 2 3 x 2 — 7 3 x 3 + 5 3 x 4 = 23 3 13 3 x 2 — 4 3 x 3 + 5 3 x 4 = 14 3

Мы исключили неизвестную переменную x 1 , теперь приступаем к исключению переменной x 2 :

— a 32 ( 1 ) a 22 ( 1 ) = — — 2 3 — 5 3 = — 2 5 и а 42 ( 1 ) а 22 ( 1 ) = — 13 3 — 5 3 = 13 5 :

3 x 1 + 2 x 2 + x 3 + x 4 = — 2 — 5 3 x 2 + 11 3 x 3 — 4 3 x 4 = — 1 3 — 2 3 x 2 — 7 3 x 3 + 5 3 x 4 = 23 3 13 3 x 2 — 4 3 x 3 + 5 3 x 4 = 14 3 ⇔

⇔ 3 x 1 + 2 x 2 + x 3 + x 4 = — 2 — 5 3 x 2 + 11 3 x 3 — 4 3 x 4 = — 1 3 — 2 3 x 2 — 7 3 x 3 + 5 3 x 4 + ( — 2 5 ) ( — 5 3 x 2 + 11 3 x 3 — 4 3 x 4 ) = 23 3 + ( — 2 5 ) ( — 1 3 ) 13 3 x 2 — 4 3 x 3 + 5 3 x 4 + 13 5 ( — 5 3 x 2 + 11 3 x 3 — 4 3 x 4 ) = 14 3 + 13 5 ( — 1 3 ) ⇔

⇔ 3 x 1 + 2 x 2 + x 3 + x 4 = — 2 — 5 3 x 2 + 11 3 x 3 — 4 3 x 4 = — 1 3 — 19 5 x 3 + 11 5 x 4 = 39 5 41 5 x 3 — 9 5 x 4 = 19 5

Для того чтобы завершить прямой ход метода Гаусса, необходимо исключить x 3 из последнего уравнения системы — а 43 ( 2 ) а 33 ( 2 ) = — 41 5 — 19 5 = 41 19 :

3 x 1 + 2 x 2 + x 3 + x 4 = — 2 — 5 3 x 2 + 11 3 x 3 — 4 3 x 4 = — 1 3 — 19 5 x 3 + 11 5 x 4 = 39 5 41 5 x 3 — 9 5 x 4 = 19 5 ⇔

3 x 1 + 2 x 2 + x 3 + x 4 = — 2 — 5 3 x 2 + 11 3 x 3 — 4 3 x 4 = — 1 3 — 19 5 x 3 + 11 5 x 4 = 39 5 41 5 x 3 — 9 5 x 4 + 41 19 ( — 19 5 x 3 + 11 5 x 4 ) = 19 5 + 41 19 39 5 ⇔

⇔ 3 x 1 + 2 x 2 + x 3 + x 4 = — 2 — 5 3 x 2 + 11 3 x 3 — 4 3 x 4 = — 1 3 — 19 5 x 3 + 11 5 x 4 = 39 5 56 19 x 4 = 392 19

Обратный ход метода Гаусса:

• из последнего уравнения имеем: x 4 = 392 19 56 19 = 7 ;
• из 3-го уравнения получаем: x 3 = — 5 19 ( 39 5 — 11 5 x 4 ) = — 5 19 ( 39 5 — 11 5 × 7 ) = 38 19 = 2 ;
• из 2-го: x 2 = — 3 5 ( — 1 3 — 11 3 x 4 + 4 3 x 4 ) = — 3 5 ( — 1 3 — 11 3 × 2 + 4 3 × 7 ) = — 1 ;
• из 1-го: x 1 = 1 3 ( — 2 — 2 x 2 — x 3 — x 4 ) = — 2 — 2 × ( — 1 ) — 2 — 7 3 = — 9 3 = — 3 .

Ответ: x 1 = — 3 ; x 2 = — 1 ; x 3 = 2 ; x 4 = 7

Найти решение этого же примера методом Гаусса в матричной форме записи:

3 x 1 + 2 x 2 + x 3 + x 4 = — 2 x 1 — x 2 + 4 x 3 — x 4 = — 1 — 2 x 1 — 2 x 2 — 3 x 3 + x 4 = 9 x 1 + 5 x 2 — x 3 + 2 x 4 = 4

Расширенная матрица системы представлена в виде:

x 1 x 2 x 3 x 4 3 2 1 1 1 — 1 4 — 1 — 2 — 2 — 3 1 1 5 — 1 2 — 2 — 1 9 4

Прямой ход метода Гаусса в данном случае предполагает приведение расширенной матрицы к трапецеидальному виду при помощи элементарных преобразований. Этот процесс очень поход на процесс исключения неизвестных переменных в координатном виде.

Преобразование матрицы начинается с превращения всех элементов нулевые. Для этого к элементам 2-ой, 3-ей и 4-ой строк прибавляем соответствующие элементы 1-ой строки, которые умножены на — a 21 a 11 = — 1 3 , — a 31 a 11 = — — 2 3 = 2 3 и н а — а 41 а 11 = — 1 3 .

Дальнейшие преобразования происходит по такой схеме: все элементы во 2-ом столбце, начиная с 3-ей строки, становятся нулевыми. Такой процесс соответствует процессу исключения переменной . Для того, чтобы выполнить этой действие, необходимо к элементам 3-ей и 4-ой строк прибавить соответствующие элементы 1-ой строки матрицы, которая умножена на — а 32 ( 1 ) а 22 ( 1 ) = — 2 3 — 5 3 = — 2 5 и — а 42 ( 1 ) а 22 ( 1 ) = — 13 3 — 5 3 = 13 5 :

x 1 x 2 x 3 x 4 3 2 1 1 | — 2 0 — 5 3 11 3 — 4 3 | — 1 3 0 — 2 3 — 7 3 5 3 | 23 3 0 13 3 — 4 3 5 3 | 14 3

x 1 x 2 x 3 x 4

3 2 1 1 | — 2 0 — 5 3 11 3 — 4 3 | — 1 3 0 — 2 3 + ( — 2 5 ) ( — 5 3 ) — 7 3 + ( — 2 5 ) 11 3 5 3 + ( — 2 5 ) ( — 4 3 ) | 23 3 + ( — 2 5 ) ( — 1 3 ) 0 13 3 + 13 5 ( — 5 3 ) — 4 3 + 13 5 × 11 3 5 3 + 13 5 ( — 4 3 ) | 14 3 + 13 5 ( — 1 3 )

x 1 x 2 x 3 x 4

3 2 1 1 | — 2 0 — 5 3 11 3 — 4 3 | — 1 3 0 0 — 19 5 11 5 | 39 5 0 0 41 5 — 9 5 | 19 5

Теперь исключаем переменную x 3 из последнего уравнения — прибавляем к элементам последней строки матрицы соответствующие элементы последней строки, которая умножена на а 43 ( 2 ) а 33 ( 2 ) = — 41 5 — 19 5 = 41 19 .

x 1 x 2 x 3 x 4 3 2 1 1 | — 2 0 — 5 3 11 3 — 4 3 | — 1 3 0 0 — 19 5 11 5 | 39 5 0 0 41 5 — 9 5 | 19 5

x 1 x 2 x 3 x 4

3 2 1 1 | — 2 0 — 5 3 11 3 — 4 3 | — 1 3 0 0 — 19 5 11 5 | 39 5 0 0 41 5 + 41 19 ( — 19 5 ) — 9 5 + 41 19 × 11 5 | 19 5 + 41 19 × 39 5

x 1 x 2 x 3 x 4

3 2 1 1 | — 2 0 — 5 3 11 3 — 4 3 | — 1 3 0 0 — 19 5 11 5 | 39 5 0 0 0 56 19 | 392 19

Теперь применим обратных ход метода. В матричной форме записи такое преобразование матрицы, чтобы матрица, которая отмечена цветом на изображении:

x 1 x 2 x 3 x 4 3 2 1 1 | — 2 0 — 5 3 11 3 — 4 3 | — 1 3 0 0 — 19 5 11 5 | 39 5 0 0 0 56 19 | 392 19

стала диагональной, т.е. приняла следующий вид:

x 1 x 2 x 3 x 4 3 0 0 0 | а 1 0 — 5 3 0 0 | а 2 0 0 — 19 5 0 | а 3 0 0 0 56 19 | 392 19 , где а 1 , а 2 , а 3 — некоторые числа.

Такие преобразования выступают аналогом прямому ходу, только преобразования выполняются не от 1-ой строки уравнения, а от последней. Прибавляем к элементам 3-ей, 2-ой и 1-ой строк соответствующие элементы последней строки, которая умножена на

— 11 5 56 19 = — 209 280 , н а — — 4 3 56 19 = 19 42 и н а — 1 56 19 = 19 56 .

x 1 x 2 x 3 x 4 3 2 1 1 | — 2 0 — 5 3 11 3 — 4 3 | — 1 3 0 0 — 19 5 11 5 | 39 5 0 0 0 56 19 | 392 19

x 1 x 2 x 3 x 4

3 2 1 1 + ( — 19 56 ) 56 19 | — 2 + ( — 19 56 ) 392 19 0 — 5 3 11 3 — 4 3 + 19 42 × 56 19 | — 1 3 + 19 42 × 392 19 0 0 — 19 5 11 5 + ( — 209 280 ) 56 19 | 39 5 + ( — 209 280 ) 392 19 0 0 0 56 19 | 392 19

x 1 x 2 x 3 x 4

3 2 1 0 | — 9 0 — 5 3 11 3 0 | 9 0 0 — 19 5 0 | — 38 5 0 0 0 56 19 | 392 19

Далее прибавляем к элементам 2-ой и 1-ой строк соответствующие элементы 3-ей строки, которые умножены на

— 11 3 — 19 5 = 55 57 и н а — 1 — 19 5 = 5 19 .

x 1 x 2 x 3 x 4 3 2 1 0 | — 9 0 — 5 3 11 3 0 | 9 0 0 — 19 5 0 | — 38 5 0 0 0 56 19 | 392 19

x 1 x 2 x 3 x 4

3 2 1 + 5 19 ( — 19 5 ) 0 | — 9 + 5 19 ( — 38 5 ) 0 — 5 3 11 3 + 55 57 ( — 19 5 ) 0 | 9 + 55 57 ( — 38 5 ) 0 0 — 19 5 0 | — 38 5 0 0 0 56 19 | 392 19

x 1 x 2 x 3 x 4

3 2 1 0 | — 11 0 — 5 3 0 0 | 5 3 0 0 — 19 5 0 | — 38 5 0 0 0 56 19 | 392 19

На последнем этапе прибавляем элементы 2-ой строки к соответствующим элементам 1-ой строки, которые умножены на — 2 — 5 3 = 6 5 .

x 1 x 2 x 3 x 4 3 2 1 0 | — 11 0 — 5 3 0 0 | 5 3 0 0 — 19 5 0 | — 38 5 0 0 0 56 19 | 392 19

x 1 x 2 x 3 x 4

3 2 + 6 5 ( — 5 3 ) 0 0 | — 11 + 6 5 × 5 3 ) 0 — 5 3 0 0 | 5 3 0 0 — 19 5 0 | — 38 5 0 0 0 56 19 | 392 19

x 1 x 2 x 3 x 4

3 0 0 0 | — 9 0 — 5 3 0 0 | 5 3 0 0 — 19 5 0 | — 38 5 0 0 0 56 19 | 392 19

Полученная матрица соответствует системе уравнений

3 x 1 = — 9 — 5 3 x 2 = 5 3 — 19 5 x 3 = — 38 5 56 19 x 4 = 392 19 , откуда находим неизвестные переменные.

Ответ: x 1 = — 3 , x 2 = — 1 , x 3 = 2 , x 4 = 7 . ​​​

Описание алгоритма использования метода Гаусса для решения СЛАУ с несовпадающим количеством уравнений и неизвестных, или с вырожденной системой матрицы

Если основная матрица квадратная или прямоугольная, то системы уравнений могут иметь единственное решение, могут не иметь решений, а могут иметь бесконечное множество решений.

Из данного раздела мы узнаем, как с помощью метода Гаусса определить совместность или несовместность СЛАУ, а также, в случае совместности, определить количество решений для системы.

В принципе, метод исключения неизвестных при таких СЛАУ остается таким же, однако есть несколько моментов, на которых необходимо заострить внимание.

На некоторых этапах исключения неизвестных, некоторые уравнения обращаются в тождества 0=0. В таком случае, уравнения можно смело убрать из системы и продолжить прямой ход метода Гаусса.

Если мы исключаем из 2-го и 3-го уравнения x 1 , то ситуация оказывается следующей:

x 1 + 2 x 2 — x 3 + 3 x 4 = 7 2 x 1 + 4 x 2 — 2 x 3 + 6 x 4 = 14 x — x + 3 x + x = — 1 ⇔

x 1 + 2 x 2 — x 3 + 3 x 4 = 7 2 x 1 + 4 x 2 — 2 x 3 + 6 x 4 + ( — 2 ) ( x 1 + 2 x 2 — x 3 + 3 x 4 ) = 14 + ( — 2 ) × 7 x — x + 3 x + x + ( — 1 ) ( x 1 + 2 x 2 — x 3 + 3 x 4 ) = — 1 + ( — 1 ) × 7 ⇔

⇔ x 1 + 2 x 2 — x 3 + 3 x 4 = 7 0 = 0 — 3 x 2 + 4 x 3 — 2 x 4 = — 8

Из этого следует, что 2-ое уравнение можно смело удалять из системы и продолжать решение.

Если мы проводим прямой ход метода Гаусса, то одно или несколько уравнений может принять вид — некоторое число, которое отлично от нуля.

Это свидетельствует о том, что уравнение, обратившееся в равенство 0 = λ , не может обратиться в равенство ни при каких любых значениях переменных. Проще говоря, такая система несовместна (не имеет решения).

• В случае если при проведении прямого хода метода Гаусса одно или несколько уравнений принимают вид 0 = λ , где λ — некоторое число, которое отлично от нуля, то система несовместна.
• Если же в конце прямого хода метода Гаусса получается система, число уравнений которой совпадает с количеством неизвестных, то такая система совместна и определена: имеет единственное решение, которое вычисляется обратным ходом метода Гаусса.
• Если при завершении прямого хода метода Гаусса число уравнений в системе оказывается меньше количества неизвестных, то такая система совместна и имеет бесконечно количество решений, которые вычисляются при обратном ходе метода Гаусса.