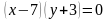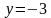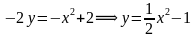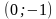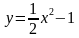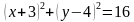Метод интервалов изображение на координатной плоскости множества решений уравнений и неравенств

Видео:Решение системы неравенств с двумя переменными. 9 класс.Скачать

Метод интервалов. Изображение на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем
презентация к уроку по алгебре (10, 11 класс)

Метод интервалов. Изображение на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем

Видео:Решение квадратных неравенств методом интервалов. 8 класс.Скачать

Скачать:

Предварительный просмотр:

Видео:Решение неравенства методом интерваловСкачать

Подписи к слайдам:

Метод интервалов. Изображение на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем

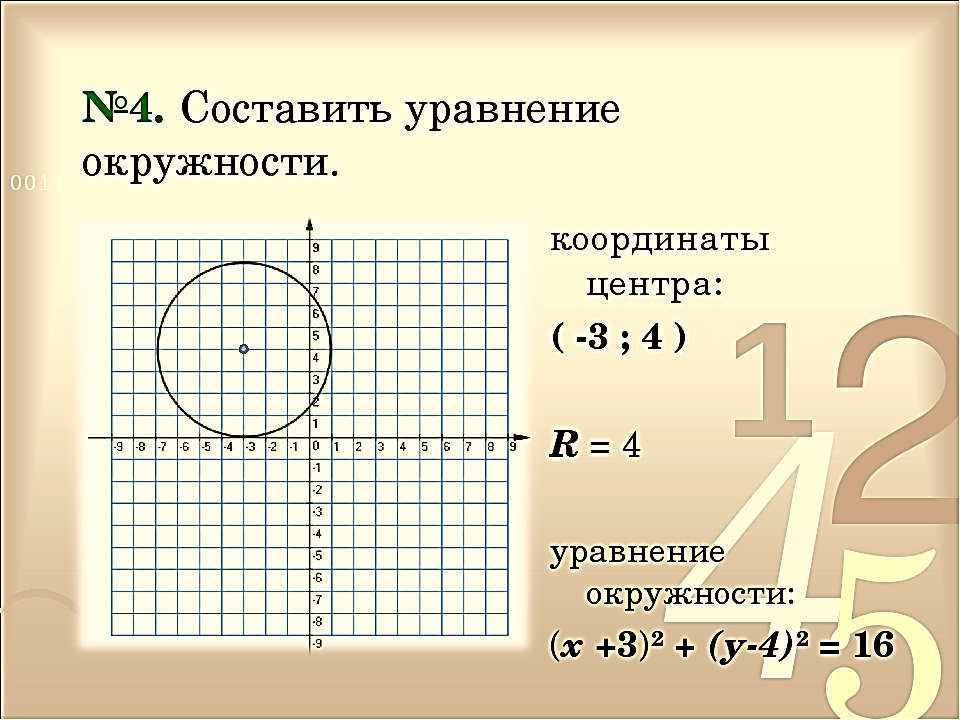
Что такое метод интервалов Метод интервалов — это специальный алгоритм, предназначенный для решения сложных неравенств вида f ( x ) > 0 и f ( x ) 0 а 0 k f(x) y 0 Задача 2. Решите неравенство: ( x + 9)( x − 3)(1 − x ) Мне нравится

Видео:Подготовка к ОГЭ . Рациональные неравенства | Математика | TutorOnlineСкачать

Изображение на координатной плоскости множества решений уравнений и неравенств с двумя переменными

Примеры изображения на координатной плоскости множества решений уравнений, неравенств и систем неравенств с двумя переменными

Просмотр содержимого документа
«Изображение на координатной плоскости множества решений уравнений и неравенств с двумя переменными»

Изображение на координатной плоскости множества решений уравнений и неравенств

с двумя переменными.

1. Изображение множества решений уравнений с двумя переменными.

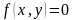
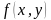
Определение. Уравнение вида , где — некоторая функция переменных х и у, называется неравенством с двумя неизвестными х и у.

Решить уравнение – значит найти множество всех его корней.

Решением уравнения с двумя переменными называется любая упорядоченная пара (х; у), которая обращает заданное уравнение в верное числовое равенство.

Для того, чтобы решить уравнение с двумя переменными нужно построить его график.

Графиком уравнения с двумя переменными является множество точек координатной плоскости, координаты которых обращают уравнение в верное равенство.

Задача 1. Изобразить на координатной плоскости множество решений уравнений

Построим график уравнения

Так как произведение равно нулю, то каждый из множителей также равен нулю.

Решим каждое из полученных уравнений:

или

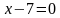
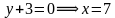
Решением является множество точек двух прямых: ,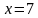

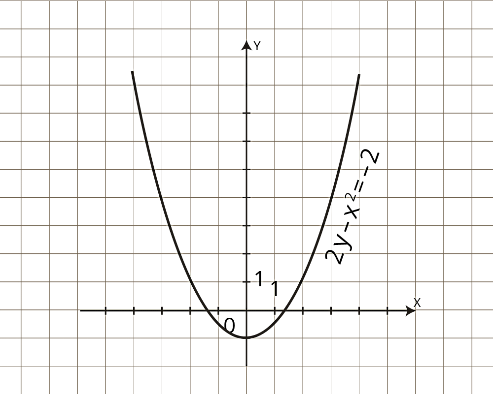
Задача 2. Изобразить на координатной плоскости множество решений уравнений

Построим график уравнения .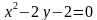

Для этого выразим переменную .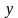

Уравнение задает параболу с вершиной в точке

То есть решением уравнения является множество точек параболы

Задача 3. Изобразить на координатной плоскости множество решений уравнений

Построим график уравнения

Уравнение задает окружность с центром в точке 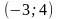, радиусом

То есть решением уравнения является множество точек построенной окружности

2. Изображение множества решений неравенств с двумя переменными.

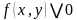
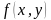
Определение. Выражение вида , где — некоторая функция переменных х и у, называется неравенством с двумя неизвестными х и у.

Решить неравенство – значит найти множество всех его решений.

Решением неравенства с двумя переменными называется любая упорядоченная пара (х; у), которая обращает заданное неравенство с переменными в верное числовое неравенство.

Алгоритм решения неравенства

1. Построить график уравнения .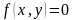

Если неравенство «строгое», тогда график изображаем пунктирной линией;

Если неравенство «нестрогое», тогда график изображаем сплошной линией.

2. Выделить штриховой часть координатной плоскости, соответствующей знаку неравенства.

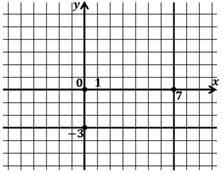
Задача 1. Изобразить на координатной плоскости множество решений неравенства

Построим график заданного неравенства . Для этого выразим переменную .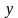

Уравнение задает линейную функцию, проходящую через точки:

Поскольку неравенство имеет знак «больше либо равно», значит выделяем часть координатной плоскости, которая лежит выше построенной прямой . Выделенная часть является решением заданного неравенства.

Задача 2. Изобразить на координатной плоскости множество решений неравенства

Построим график заданного неравенства.

Уравнение задает параболу с вершиной в точке

Поскольку заданное неравенство имеет знак «больше либо равно», значит решением неравенства является множество всех точек, расположенных выше (внутри) параболы.

Задача 3. Изобразить на координатной плоскости множество решений неравенства .

Графиком уравнения является гипербола .

Данная гипербола разбивает координатную плоскость на три области А, В и С.

Для определения необходимой области нужно выбрать контрольные точки, по одной из каждой области.

Возьмем из области А точку с координатами (5;4). Подставим координаты в заданное неравенство и проверим его истинность. Имеем: получили верное неравенство. Значит область А входит в решение заданного неравенства.

Возьмем из области В точку с координатами (1;2). Подставим координаты в заданное неравенство и проверим его истинность. Имеем: получили неверное неравенство. Значит область В не входит в решение заданного неравенства.

Возьмем из области С точку с координатами Подставим координаты в заданное неравенство и проверим его истинность. Имеем: получили верное неравенство. Значит область С входит в решение заданного неравенства.

3. Изображение множества решений системы неравенств с двумя переменными.

Решить систему неравенств – значит найти множество всех решений системы.

Решением системы неравенств с двумя переменными называется любая упорядоченная пара (х; у), которая обращает все неравенства заданной системы в верные числовые неравенства.

Системе неравенств удовлетворяют координаты тех и только тех точек, которые принадлежат пересечению множеств точек, задаваемых каждым из неравенств системы

Задача 4. Изобразить на координатной плоскости множество решений системы неравенств

На координатной плоскости множество всех решений неравенства

изображается в виде множества точек полуплоскости, лежащих выше прямой и на этой прямой (смотри задачу 1).

Аналогично строим график неравенства .

То есть строим на координатной плоскости прямую

Множество решений неравенства изображается в виде множества точек полуплоскости, лежащих выше прямой и на этой прямой.

Системе неравенств удовлетворяют координаты тех и только тех точек, которые принадлежат пересечению множеств точек, задаваемых каждым из неравенств системы.

Задача 5. Изобразить на координатной плоскости множество решений системы неравенств

На координатной плоскости множество всех решений неравенства

изображается в виде множества точек полуплоскости, лежащих ниже параболы и на этой параболе.

Аналогично, множество решений неравенства изображается в виде множества точек полуплоскости, лежащих выше параболы и на этой параболе.

Системе неравенств удовлетворяют координаты тех и только тех точек, которые принадлежат пересечению множеств точек, задаваемых каждым из неравенств системы.

Видео:Алгебра 9. Урок 7 - Неравенства. Метод интервалов - основные фактыСкачать

Разработка урока по математике «МЕТОД ИНТЕРВАЛОВ. ИЗОБРАЖЕНИЕ НА КООРДИНАТНОЙ ПЛОСКОСТИ МНОЖЕСТВА РЕШЕНИЙ УРАВНЕНИЙ И НЕРАВЕНСТВ С ДВУМЯ ПЕРЕМЕННЫМИ И ИХ СИСТЕМ.»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 300 дидактических материалов для школьного и домашнего обучения

Видео:Как понять неравенства? Квадратные неравенства. Линейные и сложные неравенства | TutorOnlineСкачать

МЕТОД ИНТЕРВАЛОВ. ИЗОБРАЖЕНИЕ НА КООРДИНАТНОЙ ПЛОСКОСТИ МНОЖЕСТВА РЕШЕНИЙ УРАВНЕНИЙ И НЕРАВЕНСТВ С ДВУМЯ ПЕРЕМЕННЫМИ И ИХ СИСТЕМ.

(Раздел «Уравнения и неравенства»)

Видео:ЧТО ТАКОЕ МЕТОД ИНТЕРВАЛОВ? ЧАСТЬ I #shorts #математика #егэ #огэ #профильныйегэ #методинтерваловСкачать

ДЕЯТЕЛЬНОСТНАЯ КАРТА УЧЕБНОГО ЗАНЯТИЯ

Профессии: 15.01.20 Слесарь по контрольно-измерительным приборам и автоматике, 09.01.03 Мастер по обработке цифровой информации, 23.01.03 Автомеханик, 09.01.01 Наладчик аппаратного и программного обеспечения

Учебные группы: КИП-11, М-11, А-11, Н-11

Учебная дисциплина: ООПу.04 Математика

Тема учебного занятия: Метод интервалов. Изображение на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем .

Тип урока: урок «открытия» новых знаний

Вид урока: лекция-беседа

— технические: мультимедийный проектор, персональный компьютер;

— информационно-коммуникационные: электронная презентация.

методическая: использование объяснительно-иллюстративного метода обучения с целью формирования математического мышления студентов;

образовательная: создание условий для овладения знаниями о методе интервалов, изображении на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем ;

развивающая: развитие умений планировать, анализировать, выдвигать гипотезы по решению заданий, применять полученные знания для выполнения упражнений;

воспитательная: воспитание интереса к изучению математики, математической культуры студентов.

− сформированность знаний о методе интервалов, изображении на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем ;

− владение умением решать задачи на методе интервалов, изображении на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем ;

— умение ставить перед собой цель, видеть ожидаемый результат работы;

— умение рационально распределять рабочее время;

— умение объективно оценивать свои возможности, анализировать свои результаты, корректировать свои действия;

— владение навыками познавательной рефлексии;

— умение осуществлять поиск и отбор необходимой информации;

— умение сопоставлять и анализировать, выделять в тексте базовые и вспомогательные концепты, опорные понятия, тезисы, структурировать их взаимосвязь ;

— умение структурировать полученную информацию ;

— умение анализировать и обобщать информацию;

— умение продуктивно общаться и взаимодействовать в процессе совместной деятельности, учитывать позиции других участников деятельности;

— умение выражать свои мысли с достаточной полнотой и точностью.

Образовательные технологии: традиционное обучение.

Формы организации обучения: фронтальная, индивидуальная.

Методы обучения и контроля:

— практические : метод сравнения, метод анализа и структурирования.

— методы контроля и самоконтроля : устный контроль, самоконтроль.

Федеральный государственный образовательный стандарт среднего общего образования (утв. приказом Министерства образования и науки Российской Федерации (Минобрнауки России) от 17 мая 2012 г. № 413 г.). – М.: Министерство образования и науки РФ, – 2012.

1. Башмаков М . И. Математика: учебник для студ. учреждений сред. проф. образования. − М.: Издательский центр «Академия», 2018. – 256 с.

2. Башмаков М . И. Математика. Сборник задач профильной направленности: учеб. пособие для студ. учреждений сред. проф. образования. − М.: Издательский центр «Академия», 2014. – 416 с.

3. Алимов Ш .А., Колягин Ю.М. Алгебра и начала математического анализа (базовый и углубленный уровни).10—11 классы. Учебник. − М.: Просвещение, 2014. – 464 с.

4. Атанасян Л.С. Геометрия. 10 − 11 классы: учебник для общеобразовательных учреждений: базовый и профильный уровни / Атанасян Л.С., Бутузов В.Ф. и др. – М.: Просвещение, 2013. – 255 с.

5. Богомолов Н.В. Практические занятия по математике: Учеб. пособие для техникумов / Н.В. Богомолов. – М.: Высш. шк., 2013. – 495 с.

6. Колягин Ю.М., Луканкин Г.Л., Яковлев Г.Н. Математика (Книга 1): Учебное пособие. – М.: Издательство «Новая волна», 2013. – 656 с.

7. Колягин Ю.М., Луканкин Г.Л., Яковлев Г.Н. Математика (Книга 2): Учебное пособие. – М.: Издательство «Новая волна», 2013. – 592 с.

8. Никольский С.М. Алгебра и начала анализа: учебник для 10 класса общеобразоват. учреждений: базовый и профильный уровни / С.М. Никольский, М.К. Потапов. – М.: Просвещение, 2013. – 430 с.

9. Никольский С.М. Алгебра и начала анализа: учебник для 11 класса общеобразоват. учреждений: базовый и профильный уровни / С.М. Никольский, М.К. Потапов. – М.: Просвещение, 2013. – 464 с.

10. Федеральный центр информационно-образовательных ресурсов [Электронный ресурс] URL : www. fcior. edu. ru

11. Единая коллекции цифровых образовательных ресурсов [Электронный ресурс] URL : www . school — collection . edu . ru

12. Инновационные педагогические технологии: учебное пособие/ Михелькевич В.Н., Нестеренко В.М., Кравцова П.Г. – Самар. гос. тех. ун-т Самара, 2001. – 89 с.

13. Кульневич С.В., Лакоценина Т.П. Современный урок. Часть 1: Научно-практич. пособие для учителей, методистов, руководителей учебных заведений, студентов пед. заведений, слушателей ИПК. – Ростов н/Д: Учитель, 2005. – 288 с.

14. Кульневич С.В., Лакоценина Т.П. Современный урок. Часть 3: Научно-практич. пособие для учителей, методистов, руководителей учебных заведений, студентов пед. заведений, слушателей ИПК. – Ростов н/Д: Учитель, 2007. – 288 с.

15. Махмутов М.И. Проблемное обучение: Основные вопросы теории. – М.: Педагогика, 1975. – 368 с.

Основные термины и понятия: метод интервалов, координатная плоскость, множества решений уравнений с двумя переменными, множества решений неравенств с двумя переменными, множества решений систем уравнений с двумя переменными, множества решений систем неравенств с двумя переменными .

Видео:Метод интервалов #1Скачать

ПЛАН УЧЕБНОГО ЗАНЯТИЯ

Содержание учебного материала:

1) Сформированность знаний о методе интервалов, изображении на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем .

2) Закрепление теоретического материала по теме с помощью решения упражнений.

1. Этап мотивации (самоопределения) к учебной деятельности (2 мин)

Преподаватель приветствует студентов, создает деловую обстановку, настраивает на продуктивную мыслительную деятельность.

2. Этап актуализации опорных знаний. Целеполагание (15 мин)

Преподаватель задает вопросы студентам:

1) Что из себя представляет метод интервалов?

2) Как изобразить уравнение на координатной плоскости?

Студенты отвечают на эти вопросы, вспоминая знания, полученные на предыдущем занятии.

Формулирование темы и целей учебного занятия.

3. Работа над новой темой («открытие» нового знания) (48 мин)

Алгоритм работы над «открытием» нового знания:

Формулирование преподавателем определений метода интервалов, изображении на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем .

Решением уравнения с двумя переменными 𝑝 ( 𝑥 ; 𝑦 )=0 называют всякую пару чисел ( 𝑥 ; 𝑦 ), которая обращает уравнение в верное числовое равенство.

Уравнение с двумя переменными обычно имеет бесконечно много решений.

уравнению 𝑥 ²+ 𝑦 ²=9 удовлетворяет любая пара ( 𝑥 ; 𝑦 ), такая, что точка координатной плоскости 𝑀 ( 𝑥 ; 𝑦 ) принадлежит окружности радиусом 3 с центром в начале координат.

Если дано целое рациональное уравнение с несколькими переменными и целочисленными коэффициентами и если поставлена задача найти его целочисленные (или рациональные) решения, то говорят, что задано диофантово уравнение.

найти целочисленные решения уравнения 3 𝑥 +4 𝑦 =19.

Выразим 𝑥 из данного уравнения: .

При делимости числа 𝑦 на 3 могут быть три возможности:

Если 𝑦 =3 𝑘 , то получим 19−4 𝑦 =19−4 ⋅ 3 𝑘 =19−12 𝑘 . Это число на 3 не делится, т. к. 12 𝑘 делится на 3, а 19 не делится на 3.

Если 𝑦 =3 𝑘 +1, то получим 19−4 𝑦 =19−4 ⋅ (3 𝑘 +1)=19−12 𝑘 −4=15−12 𝑘 =3 ⋅ (5−4 𝑘 ).

Это число на 3 делится.

Если 𝑦 =3 𝑘 +2, то получим 19−4 𝑦 =19−4 ⋅ (3 𝑘 +2)=19−12 𝑘 −8=11−12 𝑘 . Это число на 3 не делится.

Значит, единственная возможность целочисленного решения уравнения есть пара чисел (5−4 𝑘 ; 3 𝑘 +1), где 𝑘 — любое целое число.

Решением неравенства 𝑝 ( 𝑥 ; 𝑦 )>0 называют всякую пару чисел ( 𝑥 ; 𝑦 ), которая удовлетворяет этому неравенству, т. е. обращает его в верное числовое неравенство.

4. Включение нового знания в систему имеющихся знаний (20 мин)

решить неравенство 2 𝑥 +3 𝑦 >0.

Построим график уравнения 2 𝑥 +3 𝑦 =0 — прямую.

Решением неравенства являются точки полуплоскости выше или ниже построенной прямой.

Для правильного определения нужной полуплоскости выберем любую точку из неё, координаты которой подставим в данное неравенство.

Если неравенство будет верным, то полуплоскость выбрана верно.

Выбрав контрольную точку (1;1) из верхней полуплоскости, получим верное числовое неравенство: 2 ⋅ 1+3 ⋅ 1>0.

Значит, решением данного неравенства является верхняя полуплоскость.

Аналогично можно рассуждать при решении системы неравенств с двумя переменными.

Решить систему неравенств с двумя переменными — значит найти множество всех таких точек координатной плоскости, координаты которых удовлетворяют одновременно всем неравенствам системы.

5. Рефлексия. Подведение итогов учебного занятия (5 мин)

Беседа со студентами по содержанию занятия. Вопросы для беседы:

1. Какая была тема сегодняшнего занятия?

2. Что нового вы узнали?

3. Какая была цель занятия?

4. Что получилось у вас сегодня?

5. Что не получилось?

6. Достигли ли мы поставленной цели?

7. Инструктирование о выполнении домашнего задания

🌟 Видео

Как изобразить множество решений системы неравенствСкачать

9 класс - Алгебра - Системы неравенств с двумя переменными. Изображение на координатной плоскостиСкачать

9 класс - Алгебра - Неравенства с двумя переменными. Изображение на координатной плоскостиСкачать

Решение системы неравенствСкачать

Метод интервалов #3Скачать

Система уравнений VS Система неравенств. ОГЭ по математике №9, 13| Математика TutorOnlineСкачать

ПРОСТЕЙШИЙ метод решения систем квадратных неравенствСкачать

МЕТОД ИНТЕРВАЛОВ (решение неравенства)Скачать

Решение квадратных неравенств | МатематикаСкачать

Метод интервалов #4 для продвинутыхСкачать

Классический способ решения рациональных неравенств #ShortsСкачать

Как решать неравенства? Часть 1| МатематикаСкачать