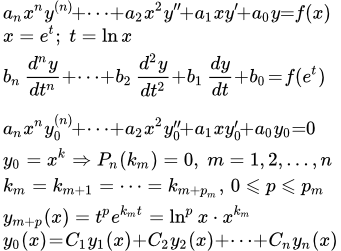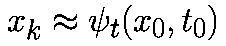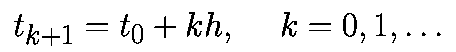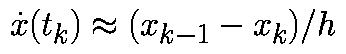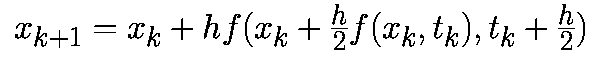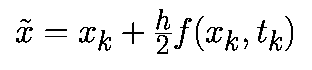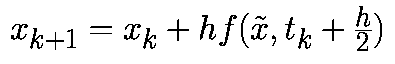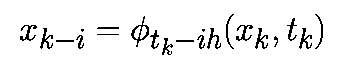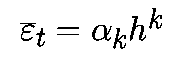Более общее уравнение Эйлера имеет вид:
.
Это уравнение подстановкой t = ax+b приводится к более простому виду, которое мы и будем рассматривать.
- Приведение дифференциального уравнения Эйлера к уравнению с постоянными коэффициентами.
- Решение однородного уравнения Эйлера
- Примеры
- Решение неоднородного уравнения Эйлера
- Пример
- Неоднородное уравнение Эйлера со специальной неоднородной частью
- Задачи с начальными условиями для систем обыкновенных дифференциальных уравнений
- Численные методы решения задачи Коши
- Явный метод Эйлера
- Программная реализация явного метода Эйлера
- Неявный метод Эйлера
- Программная реализация неявного метода Эйлера
- Методы Рунге—Кутта
- Многошаговые методы
- Жесткие системы ОДУ
- Метод интегрирования дифференциальных уравнений эйлера коши
- 📽️ Видео
Видео:Решение системы дифференциальных уравнений методом ЭйлераСкачать
Приведение дифференциального уравнения Эйлера к уравнению с постоянными коэффициентами.
Рассмотрим уравнение Эйлера:
(1) .
Оно сводится к линейному уравнению с постоянными коэффициентами подстановкой:
x = e t .
Действительно, тогда
;
;
;
;
;
.
Таким образом, множители, содержащие x m , сокращаются. Остаются члены с постоянными коэффициентами. Однако на практике, для решения уравнений Эйлера, можно применять методы решения линейных ДУ с постоянными коэффициентами без использования указанной выше подстановки.
Видео:Линейное дифференциальное уравнение Коши-ЭйлераСкачать
Решение однородного уравнения Эйлера
Рассмотрим однородное уравнение Эйлера:
(2) .
Ищем решение уравнения (2) в виде
.
;
;
.
.
Подставляем в (2) и сокращаем на x k . Получаем характеристическое уравнение:
.
Решаем его и получаем n корней, которые могут быть комплексными.
Рассмотрим действительные корни. Пусть ki – кратный корень кратности m . Этим m корням соответствуют m линейно независимых решений:
.
Рассмотрим комплексные корни. Они появляются парами вместе с комплексно сопряженными. Пусть ki – кратный корень кратности m . Выразим комплексный корень ki через действительную и мнимую части:
.
Этим m корням и m комплексно сопряженным корням соответствуют 2 m линейно независимых решений:
;
;
.
.
После того как получены n линейно независимых решений, получаем общее решение уравнения (2):
(3) .
Примеры
Видео:Численное решение задачи Коши методом ЭйлераСкачать
Решение неоднородного уравнения Эйлера
Рассмотрим неоднородное уравнение Эйлера:
.
Метод вариации постоянных (метод Лагранжа) также применим и к уравнениям Эйлера.
Сначала мы решаем однородное уравнение (2) и получаем его общее решение (3). Затем считаем постоянные функциями от переменной x . Дифференцируем (3) n – 1 раз. Получаем выражения для n – 1 производных y по x . При каждом дифференцировании члены, содержащие производные приравниваем к нулю. Так получаем n – 1 уравнений, связывающих производные . Далее находим n -ю производную y . Подставляем полученные производные в (1) и получаем n -е уравнение, связывающее производные . Из этих уравнений определяем . После чего интегрируя, получаем общее решение уравнения (1).
Пример
Видео:Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать
Неоднородное уравнение Эйлера со специальной неоднородной частью
Рассмотрим уравнение Эйлера со специальной неоднородной частью:
(4)
,
где – многочлены от степеней и , соответственно.
Наиболее простой способ решения такого уравнения заключается в том, чтобы сделать подстановку
,
и решать линейное уравнение с постоянными коэффициентами со специальной неоднородной частью.
Автор: Олег Одинцов . Опубликовано: 14-08-2013 Изменено: 24-10-2020
Видео:Метод ЭйлераСкачать
Задачи с начальными условиями для систем обыкновенных дифференциальных уравнений
Рассмотрим задачу Коши для системы обыкновенных дифференциальных уравнений $$ begin tag frac &= f_i (t, u_1, u_2, ldots, u_n), quad t > 0\ tag u_i(0) &= u_i^0, quad i = 1, 2, ldots, m. end $$
Используя векторные обозначения, задачу (1), (2) можно записать как задачу Коши $$ begin tag frac<d pmb> &= pmb(t, pmb), quad t > 0, \ tag pmb(0) &= pmb_0 end $$ В задаче Коши необходимо по известному решению в точке ( t = 0 ) необходимо найти из уравнения (3) решение при других ( t ).
Видео:Дифференциальные уравнения. Задача Коши. Метод Эйлера.Скачать
Численные методы решения задачи Коши
Существует большое количество методов численного решения задачи (3), (4). Вначале рассмотрим простейший явный метод Эйлера и его программную реализацию. Затем будут представлены методы Рунге—Кутта и многошаговые методы.
При построении численных алгоритмов будем считать, что решение этой дифференциальной задачи существует, оно единственно и обладает необходимыми свойствами гладкости.
Идея численных методов решения задачи (3), (4) состоит из четырех частей:
1. Вводится расчетная сетка по переменной ( t ) (время) из ( N_t + 1 ) точки ( t_0 ), ( t_1 ), ( ldots ), ( t_ ). Нужно найти значения неизвестной функции ( pmb ) в узлах сетки ( t_n ). Обозначим через ( pmb^n ) приближенное значение ( pmb(t_n) ).
2. Предполагаем, что дифференциальное уравнение выполнено в узлах сетки.
3. Аппроксимируем производные конечными разностями.
4. Формулируем алгоритм, который вычисляет новые значения ( pmb^ ) на основе предыдущих вычисленных значений ( pmb^k ), ( k 0 ) при ( tauto 0 ).
Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать
Явный метод Эйлера
Проиллюстрируем указанные шаги. Для начала введем расчетную сетку. Очень часто сетка является равномерной, т.е. имеет одинаковое расстояние между узлами ( t_n ) и ( t_ ): $$ omega_tau = . $$
Затем, предполагаем, что уравнение выполнено в узлах сетки, т.е.: $$ pmb^prime (t_n) = pmb(t_n, u(t_n)), quad t_n in omega_tau. $$
Заменяем производные конечными разностями. С этой целью, нам нужно знать конкретные формулы, как производные могут быть аппроксимированы конечными разностями. Простейший подход заключается в использовании определения производной: $$ pmb^prime(t) = lim_ frac<pmb(t+tau) — pmb(t)>. $$
В произвольном узле сетки ( t_n ) это определение можно переписать в виде: $$ begin pmb^prime(t_n) = lim_ frac<pmb(t_n+tau) — pmb(t_n)>. end $$ Вместо того, чтобы устремлять шаг сетки к нулю, мы можем использовать малый шаг ( tau ), который даст численное приближение ( u^prime(t_n) ): $$ begin pmb^prime(t_n) approx frac<pmb^ — pmb^>. end $$ Такая аппроксимация известна как разностная производная вперед и имеет первый порядок по ( tau ), т.е. ( O(tau) ). Теперь можно использовать аппроксимацию производной. Таким образом получим явный метод Эйлера: $$ begin tag frac<pmb^ — pmb^n> = pmb(t_n, pmb^). end $$
Четвертый шаг заключается в получении численного алгоритма. Из (5) следует, что мы должны знать значение ( y^n ) для того, чтобы решить уравнение (5) относительно ( y^ ) и получить формулу для нахождения приближенного значения искомой функции на следующем временном слое ( t_ ): $$ begin tag pmb^ = pmb^n + tau pmb(t_n, pmb^) end $$
При условии, что у нас известно начальное значение ( pmb^0 = pmb_0 ), мы можем использовать (6) для нахождения решений на последующих временных слоях.
Программная реализация явного метода Эйлера
Выражение (6) может быть как скалярным так и векторным уравнением. И в скалярном и в векторном случае на языке Python его можно реализовать следующим образом
При решении системы (векторный случай), u[n] — одномерный массив numpy длины ( m+1 ) (( m ) — размерность задачи), а функция F должна возвращать numpy -массив размерности ( m+1 ), t[n] — значение в момент времени ( t_n ).
Таким образом численное решение на отрезке ( [0, T] ) должно быть представлено двумерным массивом, инициализируемым нулями u = np.zeros((N_t+1, m+1)) . Первый индекс соответствует временному слою, а второй компоненте вектора решения на соответствующем временном слое. Использование только одного индекса, u[n] или, что то же самое, u[n, :] , соответствует всем компонентам вектора решения.
Функция euler решения системы уравнений реализована в файле euler.py:
Строка F_ = lambda . требует пояснений. Для пользователя, решающего систему ОДУ, удобно задавать функцию правой части в виде списка компонент. Можно, конечно, требовать чтобы пользователь возвращал из функции массив numpy , но очень легко осуществлять преобразование в самой функции решателе. Чтобы быть уверенным, что результат F будет нужным массивом, который можно использовать в векторных вычислениях, мы вводим новую функцию F_ , которая вызывает пользовательскую функцию F «прогоняет» результат через функцию assaray модуля numpy .
Видео:Пример решения задачи Коши методом Эйлера. Метод Эйлера с пересчетом.Скачать
Неявный метод Эйлера
При построении неявного метода Эйлера значение функции ( F ) берется на новом временном слое, т.е. для решении задачи (5) используется следующий метод: $$ begin tag frac<pmb^ — pmb^n> = pmb(t_, pmb^). end $$
Таким образом для нахождения приближенного значения искомой функции на новом временном слое ( t_ ) нужно решить нелинейное уравнение относительно ( pmb^ ): $$ begin tag pmb^ — tau pmb(t_, pmb^) — y^n = 0. end $$
Для решения уравнения (8) можно использовать, например, метод Ньютона.
Программная реализация неявного метода Эйлера
Функция backward_euler решения системы уравнений реализована в файле euler.py:
Отметим, что для нахождения значения u[n+1] используется функция fsolve модуля optimize библиотеки scipy . В качестве начального приближения для решения нелинейного уравнения используется значение искомой функции с предыдущего слоя u[n] .
Видео:МЗЭ 2022 Численное решение дифференциальных уравнений. Неявный метод Эйлера. Ложкин С.А.Скачать
Методы Рунге—Кутта
Одношаговый метод Рунге—Кутта в общем виде записывается следующим образом: $$ begin tag frac<pmb^ — pmb^n> = sum_^s b_i pmb_i, end $$ где $$ begin tag pmb_i = pmbleft( t_n + c_itau, pmb^n + tau sum_^s a_pmb_j right), quad i = 1, 2, ldots, s. end $$ Формула (9) основана на ( s ) вычислениях функции ( pmb ) и называется ( s )-стадийной. Если ( a_ = 0 ) при ( j geq i ) имеем явный метод Рунге—Кутта. Если ( a_ = 0 ) при ( j > i ) и ( a_ ne 0 ), то ( pmb_i ) определяется неявно из уравнения $$ begin tag pmb_i = pmbleft( t_n + c_itau, pmb^n + tau sum_^ a_pmb_j + tau a_ pmb_i right), quad i = 1, 2, ldots, s. end $$ О таком методе Рунге—Кутта говорят как о диагонально-неявном.
Одним из наиболее распространенных является явный метод Рунге-Кутта четвертого порядка: $$ begin tag pmb_1 & = pmb(t_n, pmb^n), &quad pmb_2 &= pmbleft( t_n + frac, pmb^n + tau frac<pmb_1> right),\ pmb_3 &= pmbleft( t_n + frac, pmb^n + tau frac<pmb_2> right), &quad pmb_4 &= pmbleft( t_n + tau, pmb^n + tau pmb_3 right),\ frac<pmb^ -pmb^n> &= frac (pmb_1 + 2pmb_2 + 2pmb_3 + pmb_4) & & end $$
Видео:16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать
Многошаговые методы
В методах Рунге—Кутта в вычислениях участвуют значения приближенного решения только в двух соседних узлах ( pmb^n ) и ( pmb^ ) — один шаг по переменной ( t ). Линейный ( m )-шаговый разностный метод записывается в виде $$ begin tag frac sum_^m a_i pmb^ = sum_^ b_i pmb(t_, pmb^), quad n = m-1, m, ldots end $$ Вариант численного метода определяется заданием коэффициентов ( a_i ), ( b_i ), ( i = 0, 1, ldots, m ), причем ( a_0 ne 0 ). Для начала расчетов по рекуррентной формуле (13) необходимо задать ( m ) начальных значений ( pmb^0 ), ( pmb^1 ), ( dots ), ( pmb^ ) (например, можно использовать для их вычисления метод Эйлера).
Различные варианты многошаговых методов (методы Адамса) решения задачи с начальными условиями для систем обыкновенных дифференциальных уравнений могут быть получены на основе использования квадратурных формул для правой части равенства $$ begin tag pmb(t_) — pmb(t_n) = int_^<t_> pmb(t, pmb) dt end $$
Для получения неявного многошагового метода используем для подынтегральной функции интерполяционную формулу по значениям функции ( pmb^ = pmb(t_, pmb^) ), ( pmb^n ), ( dots ), ( pmb^ ), т.е. $$ begin tag frac<pmb^ — pmb^n> = sum_^ b_i pmb(t_, pmb^) end $$
Для интерполяционного метода Адамса (15) наивысший порядок аппроксимации равен ( m+1 ).
Для построения явных многошаговых методов можно использовать процедуру экстраполяции подынтегральной функции в правой части (14). В этом случае приближение осуществляется по значениям ( pmb^n ), ( pmb^ ), ( dots ), ( pmb^ ) и поэтому $$ begin tag frac<pmb^ — pmb^n> = sum_^ b_i pmb(t_, pmb^) end $$
Для экстраполяционного метода Адамса (16) погрешность аппроксимации имеет ( m )-ый порядок.
На основе методов Адамса строятся и схемы предиктор–корректор. На этапе предиктор используется явный метод Адамса, на этапе корректора — аналог неявного метода Адамса. Например, при использовании методов третьего порядка аппроксимации в соответствии с (18) для предсказания решения положим $$ frac<pmb^ — pmb^n> = frac (23 pmb^ -16pmb^ + 5pmb^). $$ Для уточнеия решения (см. (17)) используется схема $$ frac<pmb^ — pmb^n> = frac (9pmb^ + 19pmb^ — 5pmb^ + pmb^). $$ Аналогично строятся и другие классы многошаговых методов.
Видео:Пример 65. Решить задачу Коши (диффуры)Скачать
Жесткие системы ОДУ
При численном решении задачи Коши для систем обыкновенных дифференциальных уравнений (3), (4) могут возникнуть дополнительные трудности, порожденные жесткостью системы. Локальные особенности поведения решения в точке ( u = w ) передаются линейной системой $$ begin frac
Пусть ( lambda_i(t) ), ( i = 1, 2, ldots, m ) — собственные числа матрицы $$ begin A(t) = < a_(t) >, quad a_(t) = frac(t, w). end $$ Система уравнений (3) является жесткой, если число $$ begin S(t) = frac <max_|Re lambda_i(t)|> <min_|Re lambda_i(t)|> end $$ велико. Это означает, что в решении присутствуют составляющие с сильно различающимися масштабами изменения по переменной ( t ).
Для численное решения жестких задач используются вычислительные алгоритмы, которые имеют повышенный запас устойчивости. Необходимо ориентироваться на использование ( A )-устойчивых или ( A(alpha) )-устойчивых методов.
Метод называется ( A )-устойчивым, если при решении задачи Коши для системы (3) область его устойчивости содержит угол $$ begin |arg(-mu)| —>
Видео:Дифференциальное уравнение. Формула ЭйлераСкачать
Метод интегрирования дифференциальных уравнений эйлера коши
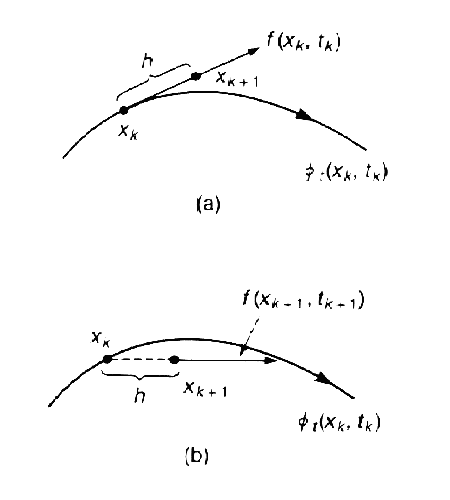
последовательностью точек x0,x1. в соответствующие моменты времени t0,t1. Значения точек должны удоволетворять приближенному равенству
Если специально не оговорено иное, то предполагается, что моменты времени выбираются через равные интервалы с величиной шага h>0, то есть
Аппроксимируем производную в момент времени tk соотношением
При такой аппроксимации уравнение (1) примет вид:
 |
 |
 |
 |
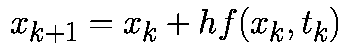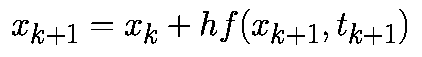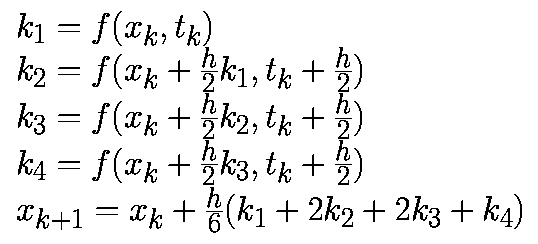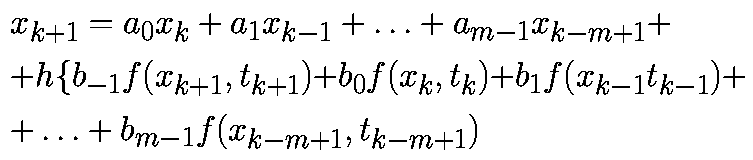