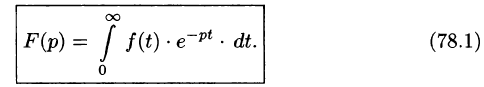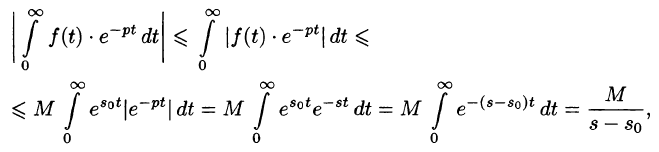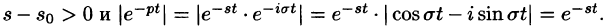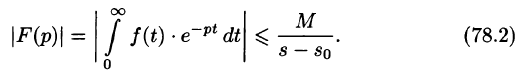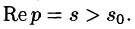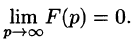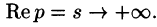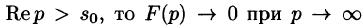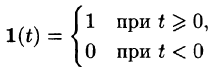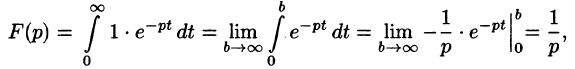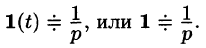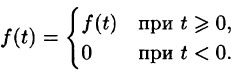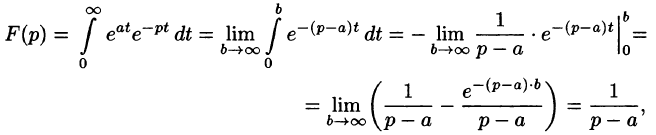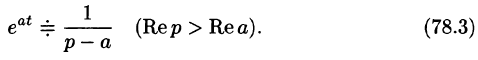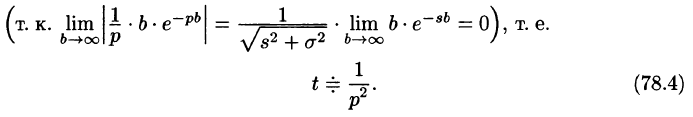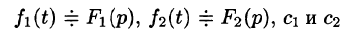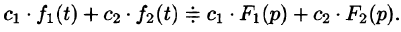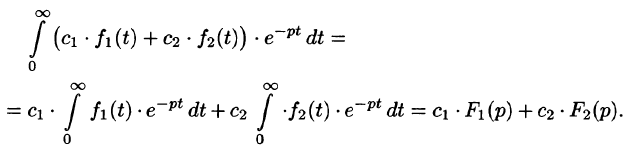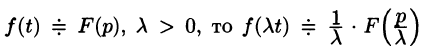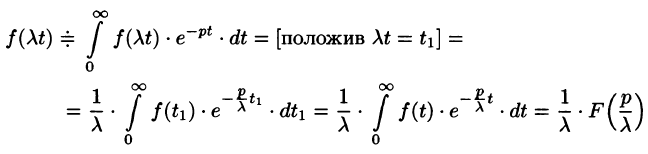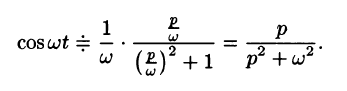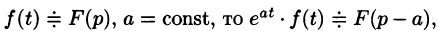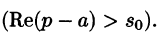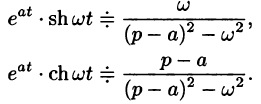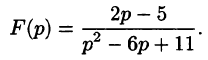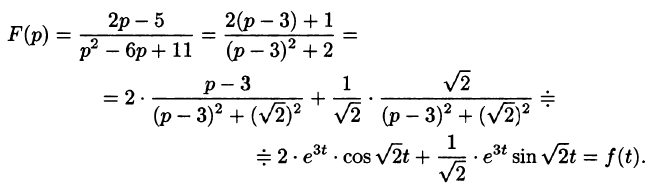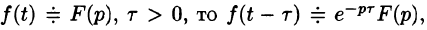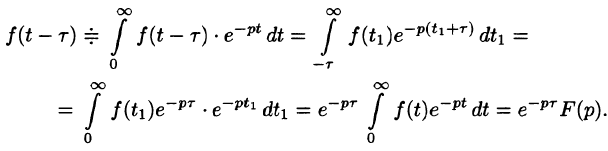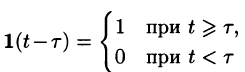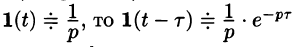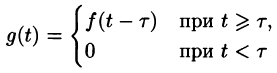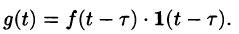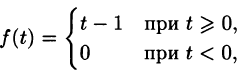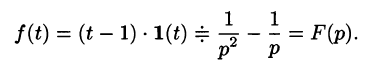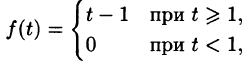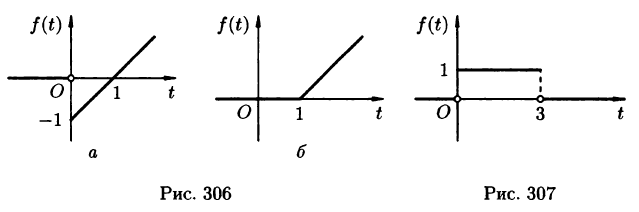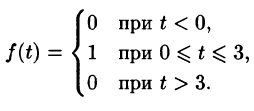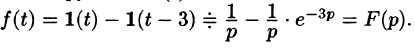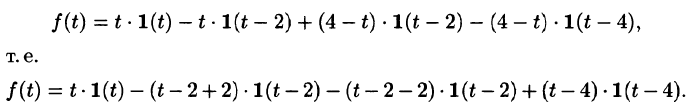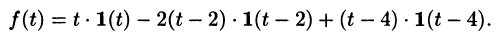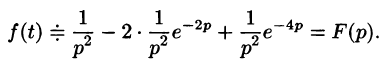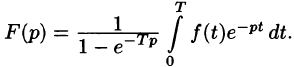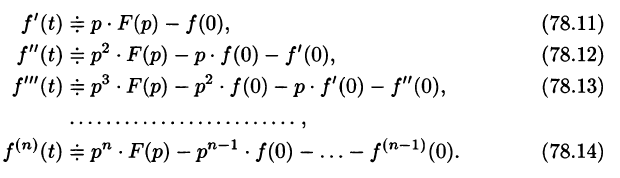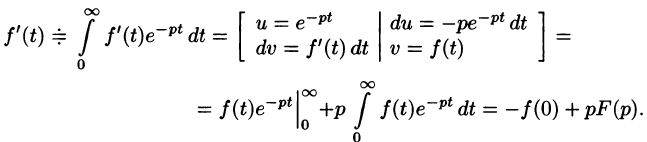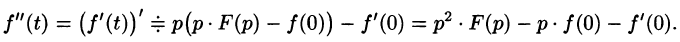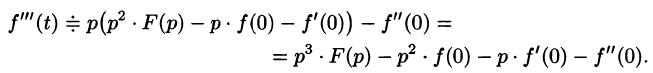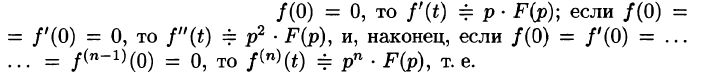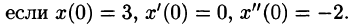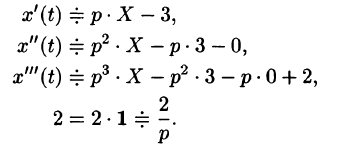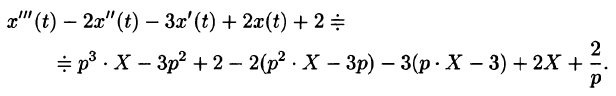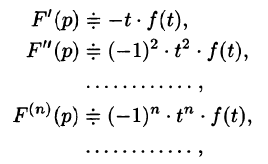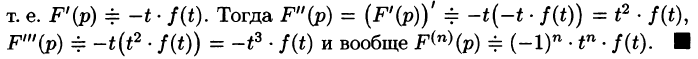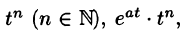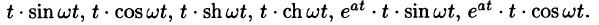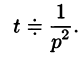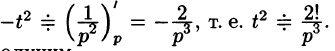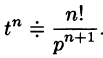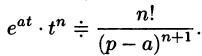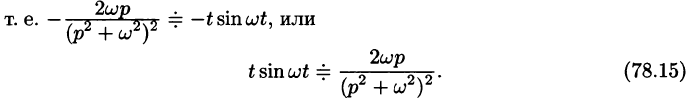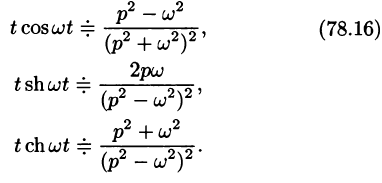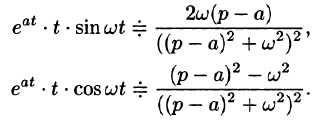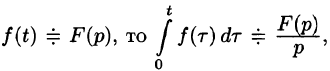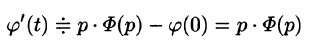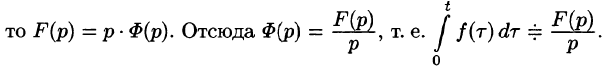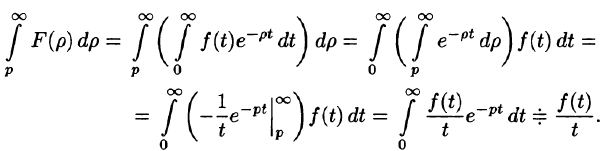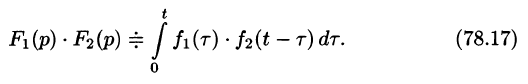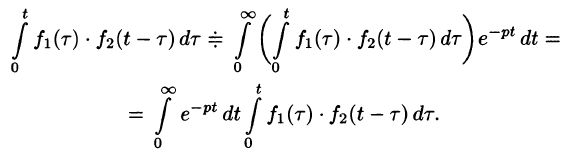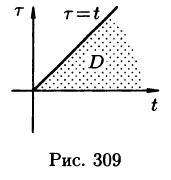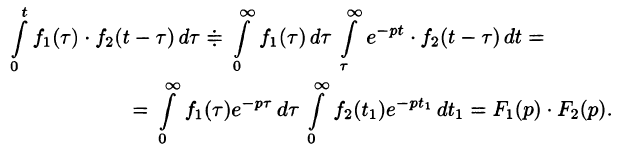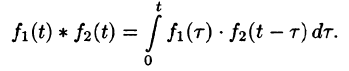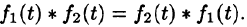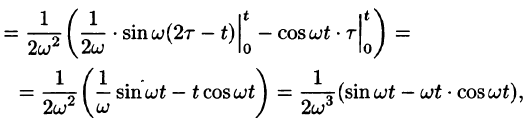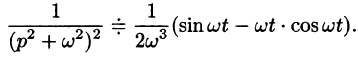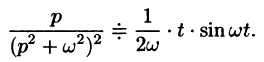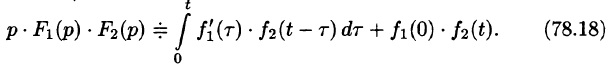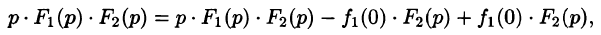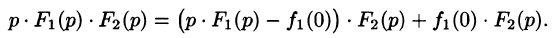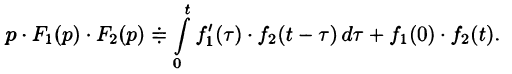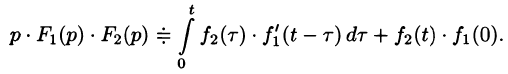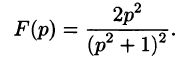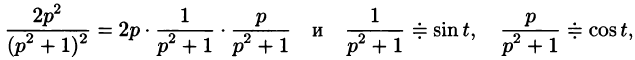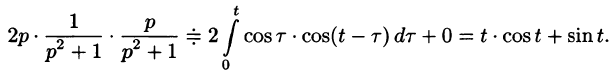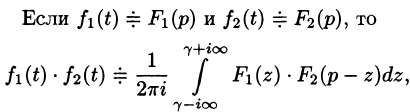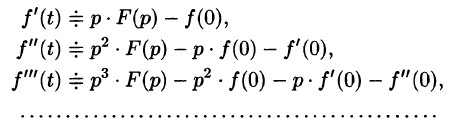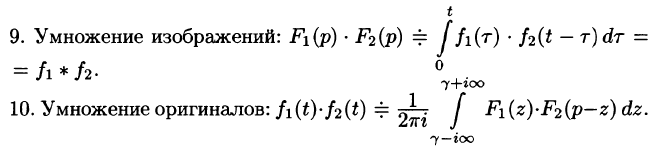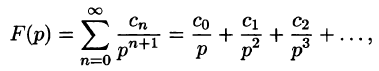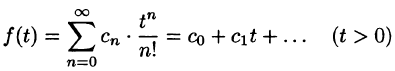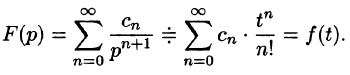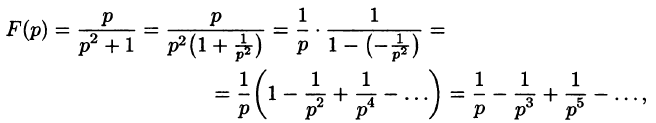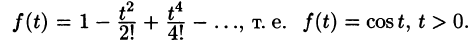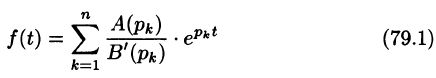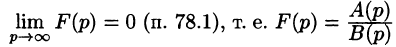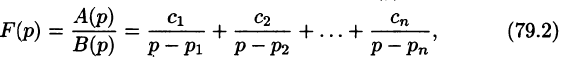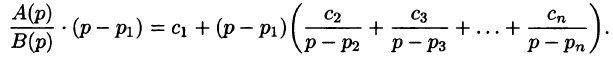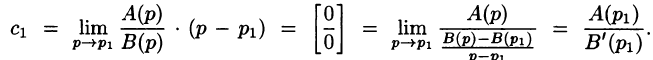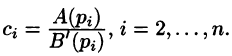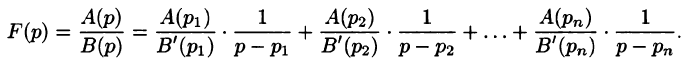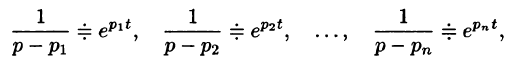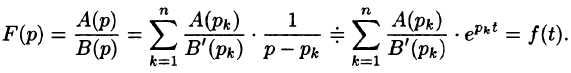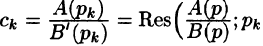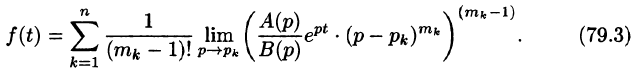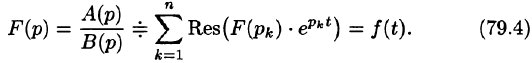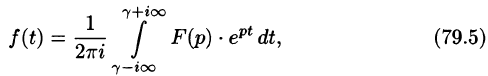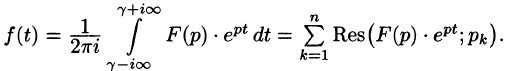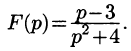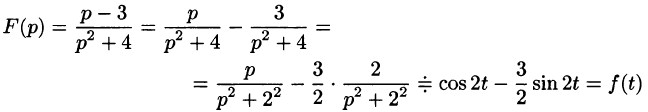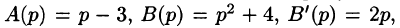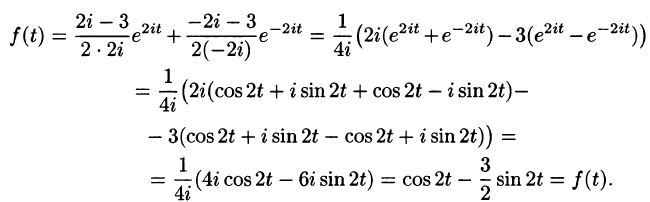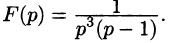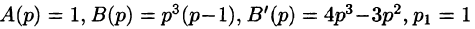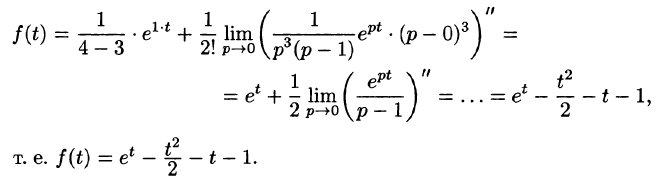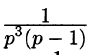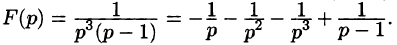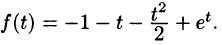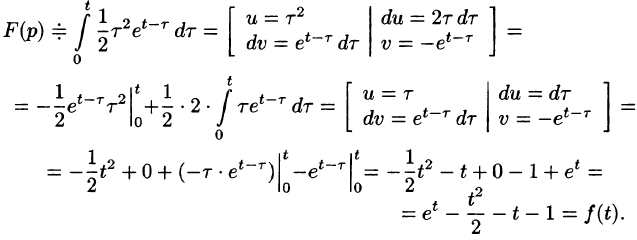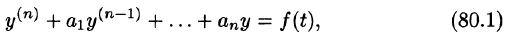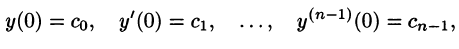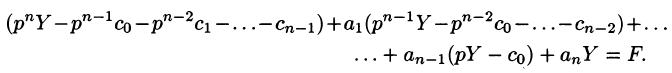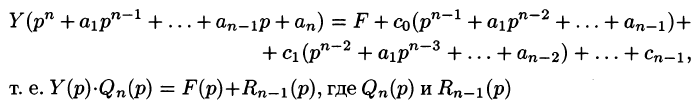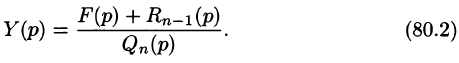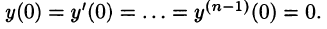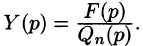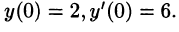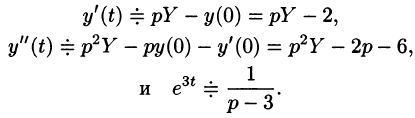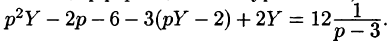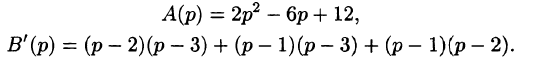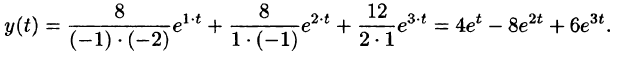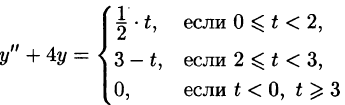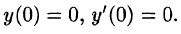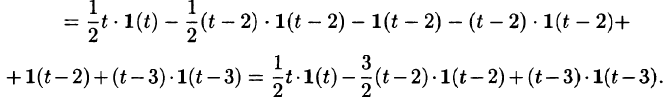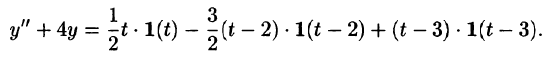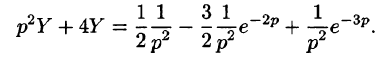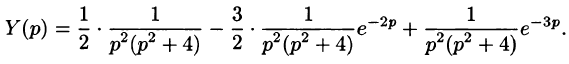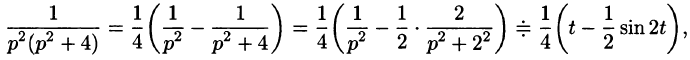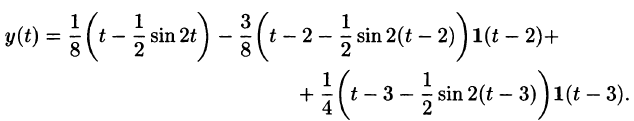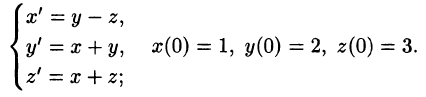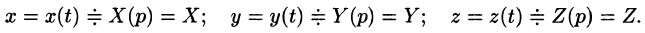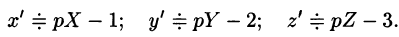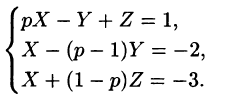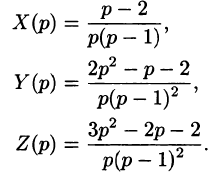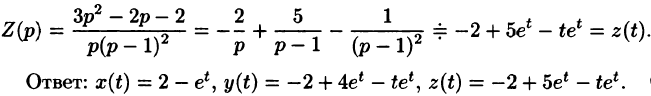ОЛИВЕР ХЕВИСАЙД
OLIVER HEAVISIDE
*
Глава третья
В 1873 г. вышла из печати двухтомная книга Максвелла «Трактат об электричестве и магнетизме». Эта книга подводила итог огромной работы по созданию теории электромагнитных явлений. В ней были Приведены знаменитые уравнения Максвелла, описывающие электромагнитное поле. Эти уравнения теперь являются основой понимания в очень широкой области явлений природы и составляют один из краеугольных камней физического знания. Но первые годы после появления этой книги мало кто понимал то, что там было сказано. Тем более мало кто понимал, что появление трактата означало появление теории. Многие ученые до Максвелла рассматривали сдельные вопросы теории электромагнетизма: электростатику, магнитное поле тока, взаимодействие двух токов и т.д. Связи между всеми этими явлениями были тогда неясны, поэтому решение каждой отдельной проблемы рассматривали как теорию. Так и говорили: теория Гаусса (статические поля), теория Ампера (магнитное поле токов), теория Био и Савара (взаимодействие двух токов) и т.д. А широкий круг оптических вопросов до Максвелла вообще не относили к области электрических и магнитных явлений.
Теория Максвелла была действительно теорией. Она описывала все упомянутые выше частные случаи — и электростатику, и магнитостатику, и взаимодействие токов, и многое другое — все те явления, о которых было известно, что они относятся к миру электричества и магнетизма. К этому же миру электрических и магнитных явлений оказалась причисленной и оптика, т.е. часть физики, изучающая законы распространения, преломления и отражения света. Максвелл показал, что свет — это электромагнитные волны малой длины.
Но в те годы, как уже было сказано, мало кто понимал, что с книгой Максвелла, наконец, появилась и теория электромагнитных явлений. Большинство ученых приняло книгу Максвелла как еще одну из многих теорий: есть теория Гаусса, Ампера, Араго, Неймана, Бебера, Био и Савара и т.д., а теперь еще появилась и теория Максвелла, и неясно, чем она лучше остальных, а может быть, она и не лучше. Особенно сильные сомнения вызывало утверждение Максвелла об электромагнитной природе световых волн и вообще предсказание о существовании электромагнитных волн. Очень немногие во всем научном мире отнеслись серьезно к теории Максвелла, когда она появилась. Скептическое отношение к ней держалось до 1888 г., когда Генрих Герц в Германии и Оливер Лодж в Англии экспериментально получили электромагнитные волны.
Хевисайд увидел книгу Максвелла вскоре после ее появления. Книга поразила его и определила всю дальнейшую жизнь. Можно было бы уточнить последние слова, написав, что книга Максвелла определила всю дальнейшую научную жизнь Хевисайда, но в таком уточнении нет нужды, если речь идет о Хевисайде. У него, кроме научной, не было никакой другой жизни. Рассказывают, что однажды кто-то сказал уже пожилому Хевисайду: «Вам надо было жениться, мистер Хевисайд». Он ответил: «Если бы я женился, что бы тогда стало с моей работой?»
Сохранилось письмо Хевисайда к Жозефу Бетено, французскому ученому, радиофизику. Письмо написано в 1918 г., когда Хевисайду было 68 лет. В письме этом рассказывается, что в молодые годы Хевисайд безуспешно старался разобраться в электрических явлениях. В 1873 г. он случайно увидел у книжного торговца только что вышедшую книгу Максвелла. Хевисайд тут же, у прилавка, прочел предисловие, проглядел текст, останавливаясь р некоторых местах для более подробного чтения, а затем прочел заключительную главу. Его охватило чувство великого открытия. Он сам писал о своем впечатлении от книги Максвелла: «Это было нечто великое, и еще более великое, и величайшее».
Джеймс Клерк Максвелл
Он сразу же купил эту книгу и с необычайным рвением приступил к ее изучению. Однако книга оказалась для него очень трудна. В этом нет ничего удивительного. Книга была трудна и для других. Один из биографов Хевисайда пишет, что Хевисайд купил у торговца не новый, а подержанный экземпляр книги Максвелла. Книга ранее принадлежала преподавателю математической физики в колледже, который против заголовка одной из глав написал: «С этого места книгу абсолютно невозможно читать» [13]. А ведь он свободно разбирался в сложных разделах высшей математики, на которых была построена математическая основа изложения в книге Максвелла. По-видимому, прежний хозяин книги не смог разобраться в физических предпосылках. из которых исходил Максвелл. Хевисайд же изучал в школе лишь элементарную математику, да и ту, как он с юмором отметил в письме к Бетено, к тому времени уже почти всю забыл. Ему понадобилось несколько лет работы, прежде чем он полностью разобрался в книге Максвелла.
Письмо заканчивается словами: «Тогда я отложил Максвелла в сторону и пошел своим собственным путем. На этот раз дело двинулось гораздо быстрее» [14].
Очень вероятно, что именно желание изучить теорию Максвелла и заставило Хевисайда уйти из телеграфной компании. До конца своей жизни он больше ни на какую другую работу не поступал. Жил он на скромные гонорары, которые получал от издателей журнала «Electrician» за публикацию своих статей. Может быть, какую-то денежную помощь ему оказывали его ближайшие родственники — родители и братья. Это, впрочем, маловероятно, потому что у Хевисайда был независимый характер и он очень неохотно принимал любую помощь. Однако во всех делах, не связанных с научными исследованиями, он был беспомощен и нуждался в уходе. Позднее британское правительство назначило ему пенсию в 120 фунтов в год в признание его научных заслуг.
После ухода с работы Оливер Хевисайд до 1889 г. жил в Лондоне в доме своего отца, где ему была отведена одна из комнат. Он неустанно занимался и большую часть времени находился в полном уединении. Обычно он закрывал окна и дверь, разжигал камин, закуривал трубку, зажигал керосиновую лампу и в невероятной жаре и духоте подолгу работал.
Хевисайд вообще любил тепло. В последние годы своей жизни, когда у него не было денег на отопление своего дома, он очень страдал от холода [6].
В семье знали, что в часы работы Оливеру нельзя мешать. Заботливая мать приносила ему еду и оставляла за дверью, так что он мог работать без помех.
Эпплъярд, автор биографии Хевисайда, описывая манеру работы молодого Оливера, меланхолически замечает: «Таким образом, он нарушал все правила, предписанные для сохранения здоровья». Правда, он тут же добавляет: «Но, с другой стороны, он много и с наслаждением ходил, а время от времени занимался и более трудными гимнастическими упражнениями, потому что он был хороший гимнаст» [12].
Оливер посещал концерты музыки, хотя ему мешала наступающая глухота. Он любил произведения «божественного Шуберта» (слова, взятые в кавычки, принадлежат Хевисайду). Однажды даже выучил на пианино одно из произведений Бетховена (ор. 90), которое любил больше других.
Эпплъярд, написавший биографию Хевисайда, упоминает, как выглядел Хевисайд в те годы: «Он был несколько ниже среднего роста, рыжеватый, сдержанный, остроумный и обладал властным характером» [12].
Имеются и другие свидетельства о том, как выглядел Хевисайд в молодые годы. Знавший его У. Браун пишет: «Как младший клерк телеграфа я работал с Оливером Хевисайдом в 1870 г. Это был молодой человек очень джентльменского вида, всегда хорошо одетый, стройный, с красивыми волосами и румяным лицом». Другие описывают его как молодого человека приятной наружности, тщательно одетого, с блестящими глазами, красивым цветом лица и светло-каштановыми волосами [6].
Мы остановились на внешности Хевисайда потому, что после него осталось только несколько его фотографий, относящихся к 1893 г., т.е. к гораздо более позднему времени. Используя эти фотографии (точнее, негативы), сделанные племянником Хевисайда Чарлзом, художник Фрэнсис Ходж написал в 1945 г. портрет Оливера Хевисайда для Института инженеров-электриков. Написать портрет в красках по черно-белой фотографии — дело нелегкое. Ходж встречался с немногими из доживших до 1945 г. людей, которые еще помнили Хевисайда, и воспользовался их советами (этот портрет помещен на странице с оглавлением).
Хевисайд не любил фотографироваться, после него осталось очень мало фотографий. Сохранилась фотография Хевисайда. где он стоит, засунув руки в карманы брюк. Негатив этой фотографии, как и несколько других, охранился в коробке, на которой рукой Хевисайда написано: «. сохранять сухими, эмульсия к эмульсии. Негатив, где руки в карманах, по-видимому, наилучший, хотя его мать предпочитала улыбку». Может быть он пишет о себе в третьем лице ( «его мать» ), а может быть он имеет в виду мать своего племянника, жену своего брата Чарлза.
Других фотографий Хевисайда, кроме тех, что сделаны по негативам из этой коробки, нет (если не считать групповых фотографий большой семьи Хевисайдов, где Оливер обычно находится на заднем плане и его лицо с трудом можно разобрать). Хевисайд высмеивал тех, кто публикует свои фотографии:
«Это заставляет общественных деятелей думать, что они в самом деле являются очень важными людьми и что поэтому неотъемлемая часть их деятельности — это стоять у порога для того, чтобы их фотографировали».
«Гиганты сзади. Пигмеи впереди. Я отдал ее, в рамке и под стеклом, мебельному торговцу в Ньютон Эбботе даром, в придачу к старому кухонному столу» [12].
«Если бы Вы были один из тех, чья высокая репутация достигнута бесцеремонным проталкиванием, я мог бы понять Ваши опасения, что опубликование Вашего портрета будет неправильно истолковано» [12].
Но вернемся к рассказу о жизни Хевисайда после того, как он ушел с работы в телеграфной компании.
Первые несколько лет, как мы уже знаем, Хевисайд посвятил изучению максвелловской теории. Прежде всего следовало овладеть математическим аппаратом — изучить дифференциальное и интегральное исчисления, дифференциальные уравнения в частных производных и многое другое. С этой задачей Хевисайд успешно справился. За очень короткое время он в совершенстве изучил все необходимые для него разделы математики (это само по себе вызывает почтительное удивление), а в дальнейшем даже создал две новые области математической физики — векторное исчисление, включая векторный анализ, и операционное исчисление. Теперь начала векторного исчисления преподают в школьном курсе математики и физики, но в то время, около ста лет назад, хотя понятие вектора и было известно, практически никто не использовал это понятие для описания физических явлений. Векторная алгебра и векторный анализ были почти не разработаны.
Как писал впоследствии Хевисайд,
«в своем великом трактате об электричестве и магнетизме Максвелл хотя и отмечал, что векторные методы подходят для рассмотрения вопроса, но не пошел дальше использования в первую очередь представления о векторе и иногда выражал свои результаты в векторной форме. Таким путем его читатели познакомились с представлением о векторе, а также узнали, как выглядят некоторые формулы, записанные в кватернионных обозначениях. Они, однако, не получили никаких сведений о том, как работать с векторами» [15].
«В теории кватернионов повелителем является кватернион, и он устанавливает свои законы для вектора и скаляра. Все вращается вокруг кватерниона. Даже законы векторной алгебры выражаются через кватернионы с помощью мнимой единицы» [6].
Сторонником векторного, а не кватернионного исчисления, кроме Хевисайда, был также Гиббс, который в своих лекциях независимо от Хевисайда (и несколько раньше) также систематически излагал основы векторного исчисления и широко применял векторное описание.
Вопрос о том, какую математическую схему выбрать для описания — векторное или кватернионное исчисление, с чисто математической точки зрения не является существенным, потому что обе эти схемы приводят к одним и тем же результатам.
Но в теории электромагнитного поля векторное описание имело определенные физические преимущества хотя бы потому, что электрическое и магнитное поля в трехмерном пространстве являются векторами, а не кватернионами, поэтому векторное описание обладает большей физической наглядностью. Аналогично обстояло дело и в других областях физики.
Введение векторного исчисления не обошлось без споров со сторонниками кватернионного описания. Гиббса и Хевисайда называли врагами кватернионного прогресса. Им приходилось отстаивать свою точку зрения.
В наше время кватернионное описание почти не применяется в физике, векторное же исчисление (его называют иногда «векторное исчисление Гиббса-Хевисайда») нашло широкое применение во многих разделах физики. Если говорить о теории Максвелла, то векторный способ изложения сделал ее более наглядной и более доступной для изучающих.
Второй вклад Хевисайда в математику — это создание операционного исчисления. Он разработал новый эффективный метод решения линейных дифференциальных уравнений. В этом методе операция дифференцирования по одной из переменных заменяется умножением дифференцируемой функции на некоторый символ, который до поры до времени может рассматриваться как простое число. Такая замена упрощает уравнение, а если искомая функция зависит только от одной переменной, то дифференциальное уравнение превращается в алгебраическое. Затем упрощенное уравнение решается обычными методами, а в полученном выражении символ, заменяющий операцию дифференцирования, вновь обретает свой первоначальный смысл. Таким образом, решение является некоторым оператором, который нужно применить к заданной функции, чтобы получить решение в явном виде. Хевисайд показал, что для большого класса физически важных задач получение решения таким методом сводится к выполнению ряда стандартных операций, которые и были им выполнены.
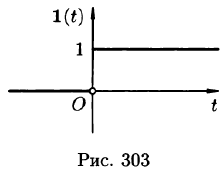
Операционное исчисление получило широкое применение при решении целого ряда задач в различных областях физики: в теории теплопроводности и диффузии, при изучении электрических цепей и линий связи, в- задачах распространения радиоволн. Удобство этого метода, помимо стандартности вычисления, состоит в том, что таким способом можно эффективно рассматривать процессы установления, или, как говорят, переходные процессы. Рассмотрим для примера некоторую электрическую цепь с отключенным элементом питания. Пусть в некоторый момент времени (скажем, в нулевой момент) элемент питания включается в цепь. Тогда, прежде чем в цепи установятся стационарные токи, должно пройти некоторое время. Операционное исчисление позволяет легко определять поведение цепи непосредственно после включения, когда токи еще не достигли стационарной величины. Для рассмотрения процессов включения Хевисайд ввел специальную функцию. Она так и называется — функция Хевисайда. Эта функция равна нулю во все отрицательные моменты времени и равна единице во все положительные моменты времени.
| |
Рис. 3. Фрагменты книги Хевисайда «Электромагнитная теория» (т. 2)
a — определение импульсной функции (оно совпадает с определением дельта-функции, которое дается в современных учебниках по теоретической физике);
б — разложение импульсной функции в ряд Фурье по синусам;
в — разложение импульсной функции в ряд Фурье по косинусам и представление произвольной функции с помощью этого разложения;
г — разложение импульсной функции в ряд Фурье на отрезке от 0 до 2l;
д — разложение импульсной функции в интеграл Фурье.
Pиc 4. Рисунок из книги Хевисайда «Электромагнитная теория» (т. 2) —
графики, условно изображающие разложения импульсной функции в ряды по синусам, косинусам и в полный ряд Фурье
Такое воздействие имеет место, например, при упругом соударении двух жестких шаров. Силы действуют на шары только в момент соударения, а интеграл от силы по времени, т.е. переданный при соударении импульс, отличен от пуля. Импульсная функция определяет также плотность точечного источника. Хевисайд подробно разобрал свойства этой функции. Однако эти работы Хевисайда были забыты. Больше чем через тридцать лет эту функцию заново ввел в физику Дирак. Теперь импульсная функция Хевисайда часто применяется в теоретической физике и носит название дельта-функции Дирака.
Работы Хевисайда по операционному исчислению первоначально не получили признания математиков.
Почему так произошло?
Хевисайд был самоучка. Он не учился в университете (и даже в средней школе последней ступени), не слушал лекций, не посещал семинарских занятий, т.е. не прошел того пути, на котором было воспитано подавляющее большинство английских ученых. Все свои знания он добыл без помощи преподавателей. Но обучение в университете давало не только научные знания. Обучение было одновременно и воспитанием в духе научных традиций, и введением в научное сообщество. Человек, окончивший Кембриджский или Оксфордский университет, уже в силу только этого факта мог рассчитывать на внимательное отношение к себе и к своим научным результатам со стороны многих и многих ученых, прошедших ту же школу, тот же путь научного воспитания. Если научные результаты не вызывали сомнения, они получали безоговорочную поддержку, если результаты вызывали возражения, автор мог рассчитывать на доброжелательную критику. Он был равноправным членом научного сообщества.
Хевисайд не вошел в научное сообщество, как теперь говорят, «не вписался». Его подход к проблеме был нетрадиционным, непривычным для членов научного сообщества и столь же непривычной была манера изложения полученных результатов. Занимаясь в полном уединении, он выработал свой стиль выбора и рассмотрения научной проблемы, и этот стиль был в некоторых отношениях далек от традиционного. Он создал свой язык и свою систему образов в науке, и они тоже отличались от традиционных. Поэтому его работы было трудно читать. Иногда труднее было понять, в чем заключается утверждение Хевисайда, чем убедиться в справедливости этого утверждения.
Нужно еще помнить, что Хевисайд работал, как теперь говорят, «на переднем крае науки», он занимался новыми для своего времени проблемами. В таких случаях всегда можно требовать соблюдения традиций в научном подходе. Бывает так, что при изучении нового класса явлений традиционный научный подход оказывается несостоятельным и тогда зарождается новая традиция. Современники не всегда могут это увидеть и оценить. Несомненно, что и Максвелл при жизни не получил того придания, какого он достоин за свою электромагнитную теорию.
Научная традиция налагала определенные условия и на тематическое рассмотрение физических проблем. Все тематическое описание физических явлений нужно было проводить на высоком уровне математической строгости, т.е. не выходя за пределы применимости строго доказанных математических утверждений. Выполнить это требование в полном объеме было очень трудно, да и вряд ли нужно. Математический аппарат в физических исследованиях играет подчиненную роль, а основная задача здесь — выяснение физических особенностей явления. В этих условиях может получиться так, что выполнение всех требований строгости математического описания может не помогать выяснению физики дела, а, наоборот, затруднять выяснение. Неудивительно, что время от времени даже столь известным людям, как Максвелл и Рэлей, предъявлялись упреки за уклонение от математической строгости. Отвечая на эти упреки, Рэлей в предисловии ко второму изданию своей книги «Теория звука» писал:
«В математическом исследовании я обычно использовал методы, которые представляются естественными для физика. Чистый математик будет сожалеть, и (надо признать) иногда с основанием, о недостатке строгости. Но у этого вопроса есть две стороны. Потому что, сколь бы ни было важно сохранять высокие стандарты в чистой математике, физик иногда хорошо делает, что довольствуется соображениями, которые, с его точки зрения, вполне удовлетворительны и убедительны. Он использует представления другого порядка, и более строгий образ действий чистого математика может показаться ему не более, а менее доказательным. И, кроме того, во многих затруднительных случаях требование высочайшего уровня означало бы вообще отказ от рассмотрения данного вопроса из-за объема, который для этого требуется» [17].
Математики отказывались признавать функцию Хевисайда, которая не была непрерывной и дифференцируемой, они отказывались признавать импульсную функцию, которая отлична от нуля только в одной точке, а интеграл от этой функции все же не равен нулю. Отказывались они и от признания результатов, полученных с использованием этих функций.
Математики возражали против того, что Хевисайд заменил операцию дифференцирования значком, а затем обращался с этим значком как с алгебраической величиной. А Хевисайд сделал еще много такого, чего никакой строгий математик в то время не признал бы. Он ввел функцию, аргументом которой был оператор (скажем, оператор дифференцирования), и разлагал эту функцию в .ряд по степеням оператора. Как можно было определить сходимость такого ряда? Ведь его членами были но числа и не функции, а операторы. Он ввел производную дробного порядка, он разлагал функции в расходящиеся ряды. Все это привело к тому, что методы Хевисайда математики рассматривали как нестрогие, а значит, вообще не считали за методы.
Сохранилось письмо Рэлея к Хевисайду, где Рэлей пишет об одной из работ Хевисайда:
«. Эта работа не понравилась нашим математикам. Они считают, что значительная часть работы представляет собой попытку сделать с помощью несовершенных методов то, что уже сделано с помощью строгих методов» [7].
Отношение математиков из Королевского, общества вызывало обиду Хевисайда в течение многих лет. Дело было не только в недооценке его методов, которые со временем все получили обоснование. В частности, его импульсная функция получила полные права математического гражданства в теории обобщенных функций лет через 50 после того, как импульсную функцию систематически использовал Хевисайд, получивший с ее помощью ряд важных физических результатов. Обосновано было и операционное исчисление, причем обоснование теперь представляется довольно простым делом. В общих словах обоснование это таково.
Рис 5. Фрагмент книги Хевисайда «Электромагнитная теория» (т. 2) —
решение дифференциального уравнения с помощью операторных методов, разработанных Хевисайдом.
Формула (81) определяет так называемый оператор смещения
Возьмем функцию вида А е pt , где р и А — некоторые постоянные числа, a t независимая переменная. Дифференцирование этой функции по переменной t сводится к умножению на р , вычисление второй производной дает множитель p 2 и т.д. Мы видим, что для этой функции оператор дифференцирования можно заменить числом р , как этой делал Хевисайд. Функция А е pt является, как теперь говорят, собственной функцией оператора — d/dt — с собственным значением р . В базисе, построенном из собственных функций, оператор есть число. Но любую функцию от переменной t можно представить в виде суммы функций вида А е pt , подобрав для каждого значения р свое значение А . Такое представление — это хорошо известное интегральное представление Лаплаcа (или Фурье). Таким образом, операционный метод Хевисайда применим для широкого класса функций, которые могут быть представлены в виде интеграла Лапласа (или Фурье). Отметим, кстати, что слово «оператор» и соответствующее этому слову понятие вошло в физику в значительной мере благодаря Хевисайду.
В работах Пуанкаре, Бореля, Таубера и других математиков даны методы строгого обоснования применявшихся Хевисайдом асимптотических разложений.
Хевисайд неоднократно выражал свое отношение к требованию математической строгости на самом высшем уровне при изложении физических теорий. Он, в частности, писал:
«Нужно по возможности полнее избегать вошедшего в обычай избавления от физики путем сведения задачи к чисто математическому упражнению. Следует все время не упускать из вида физику, чтобы придать задаче жизнь и реальное значение и чтобы получить большую помощь, которую физика дает математике. Это не всегда может быть сделано, особенно в деталях, которые требуют больших вычислений, но этот общий принцип следует проводить в жизнь по возможности полнее, уделяя особое внимание движущим идеям. Ни один математический пурист никогда бы не смог выполнить работу, заключенную в максвелловском трактате. Он мог бы знать всю необходимую математику и даже больше, но это не привело бы к цели, потому что он не смог бы сложить все вместе без физического руководства. Это обстоятельство ни в коей мере его не позорит, но только показывает различие в путях мышления. За последние полвека чистая математика достигла огромных успехов, и было бы правильной справедливо поставить их в соответствие с успехами в физической науке. Но вместе с тем к пуристам пришла склонность возражать против введения физических идей в математику с возможной в результате потерей строгости. Может оказаться, что иногда не только не происходит потери строгости, но увеличивается общность и упрощается рассмотрение» [18].
«. И я бы еще добавил к этому, что если случится физику зайти слишком далеко, то, чтобы не прерывать работы, было бы правильно отложить на последующее время отыскание ограничений и поправок. Но такой процесс очищения подобает в гораздо большей степени проводить пуристу. Если одно из этих дел столь же необходимо, как другое, то ясно, что физик мало бы чего достиг, пытаясь делать оба этих дела из опасения перед поборниками строгости. Что может быть ненавистнее, чем физическая работа, состоящая из предложений и следствий? Она достаточно плоха и как чисто математическая, и я хотел бы, чтобы пуристы взяли урок у Фурье, Томсона и Тэта, Максвелла или Рэлея и чтобы они излагали свою повесть иначе и сделали бы ее интереснее, допустив немного воображения. Я имел возможность ознакомиться со значительной частью большой книги по теории функций, пытаясь найти там то, чего я не нашел. Самое большое восхищение вызывают старательность и суровая строгость, но как это отличается от физической математики, как трудно что-то вычитать из сурового формализма, и насколько узкой кажется книга из-за недостатка физических примеров. Пожалуй, вопрос прояснился бы в значительной степени, если бы имелась физическая теория, основанная на этом материале или поясняющая его» [19].
Хевисайд не отрицал, что применяемые им математические методы еще не имели в то время строгого обоснования. Но он считал, что если метод доказал свою эффективность, то нужно этот метод применять, не дожидаясь строгого обоснования. Он приводит в пример введенные им операторы сопротивления электрической цепи:
«Действительно, их использование часто ведет к большим упрощениям и избавляет от необходимости проводить сложные вычисления определенных интегралов. Но при этом строгая логика дела не ясна! Ну и что из того? Буду ли я отказываться от обеда потому, что не понимаю полностью процесс пищеварения? Нет, не буду, если я удовлетворен результатом. Подобным образом и физик может применять нестрогие процессы с удовлетворением и пользой, если он, проводя проверки, убеждается в точности своих результатов» [20].
Но в приведенных высказываниях Хевисайда о чистой математике есть и такое, с которым согласится всякий. Хевисайд утверждает, что успехи математики связаны с успехами физической науки. Строгая математическая физика времен Хевисайда в конечном счете уходит корнями в ньютоновскую механику. Те, кто упрекал Хевисайда в математической нестрогости, не понимали, что наступает время новой физики, которая не сводится к ньютоновской механике. А новая физика требовала новой математики, и Хевисайд это понимал. В частности, когда его упрекали за применение расходящихся рядов, которые тогда не рассматривались в теории функций, он отвечал: «А как насчет теории функций, которая сознательно отказывается от рассмотрения расходящихся рядов? Может ли она действительно быть теорией функций? Разве не нужна теория с большим охватом, объединяющая и сходящиеся и расходящиеся ряды в единое гармоническое целое?» [21].
Добавим еще, что, насколько известно, обвинения против Хевисайда в математической нестрогости и в применении необоснованных методов никогда не сопровождались конкретным указанием на ошибочность тех или иных результатов, полученных Хевисайдом. Хевисайд вычислял правильно, может быть, как раз потому, что он как никто другой мог провести физический анализ проблемы.
Если попытаться коротко сказать о существе спора между Хевисайдом и поборниками строгости в математике, то можно сказать, что Хевисайд подчеркивал большую роль интуиции в научном познании. Он вовсе не умалял роль логического познания. Но он понимал, что нельзя чисто логическим путем вывести законы природы из известной нам совокупности фактов. По этому поводу Эйнштейн высказывался даже более определенно. Эйнштейн считал, что никакого логического пути от данных опыта к формулировке законов природы не существует. В этом смысле связь между данными опыта и законами природы, по Эйнштейну, является интуитивной.
Приведем здесь слова А. Эйнштейна о роли интуиции в науке:
«Я верю в интуицию и вдохновение. Иногда я чувствую, что стою на правильном пути, но не могу объяснить свою уверенность. Когда в 1919 г. солнечное затмение подтвердило мою догадку, я не был ничуть удивлен. Я был бы изумлен, если бы этого не случилось. Воображение важнее знания, ибо знание ограниченно, воображение же охватывает все на свете, стимулирует прогресс и является источником эволюции. Строго говоря, воображение — это реальный фактор в научном исследовании».
По существу, поборники строгости критиковали Хевисайда за то, что он не проводил строгого логического обоснования разработанных им новых математических методов. Они не понимали того, что действительно новое не может быть выведено чисто логическим путем на основе известного старого. В познании мира логическое и интуитивное начала не исключают, а дополняют друг друга [135].
Приведем еще одно рассуждение Хевисайда о путях научного исследования.
«Сопоставляя н согласуя между собой разные части единой теории н убеждаясь в ее согласованности, мы приходим к пониманию теории. Мы можем начать где угодно и двигаться любым путем. Конечно, некоторые пути будут предпочтительны, потому что они могут быть легче или дают широкий и ясный обзор, но нет необходимости строго придерживаться определенного курса. Это, может быть, даже н нежелательно. Может быть, более интересно и поучительно не идти по кратчайшему логическому курсу от одной точки к другой. Может быть, лучше бродить, и руководствоваться обстоятельствами при выборе пути, и не закрывать глаза на виды по сторонам, а в дальнейшем менять маршруты, чтобы посмотреть на ту же страну с других точек.
Ясно, что если нужно провести кого-то по хорошо известной стране, уже хорошо исследованной, то лучше придерживаться некоторых определенных дорог. Но дело обстоит несколько иначе в случае исследования сравнительно неизвестной области с непроходимыми джунглями, горами и пропастями. В этом случае было бы абсурдно следовать логическим курсом от одной точки к другой.
Вам надо быть бдительным и непредубежденным и руководствоваться обстоятельствами. Прежде всего вам нужно выяснить, что именно следует выяснить. Как вы это делаете — это уже совсем другое дело. Без сомнения, впоследствии будут найдены пути гораздо более легкие и, может быть, лучшие, и по этим путям сможет пройти толпа.
Я полагаю, ясно, что жалобы на недостаток совершенства в выборе путей и в образе действий исследователя со стороны людей, привыкших к более строгим методам, в значительной степени смехотворны. Хотя и безвредные по намерению, они могут действовать несправедливо, если приводят, как иногда бывает (совсем недавно я узнал про такого рода случай), к отклонению самой добросовестной работы, которая не смогла быть признана судьями, имеющими, без сомнения, другой образ действий и мыслей и другой жизненный опыт. Когда такое происходит, это ставит ученое сообщество в положение, достойное сожаления: кажется, что сообщество существует не только для поощрения исследований по установленным направлениям, но также и для того, чтобы активно противодействовать работам не столь общепринятого характера.
Невозможно поверить, что именно так и обстоит дело в действительности. Но, с другой стороны, статьи ценятся так дешево, одной больше, одной меньше — какая разница?
И опять, вероятно, судьи были одушевлены доброжелательными побуждениями и хотели только увести заплутавшегося автора с его ошибочных путей и вывести на более строгие одобряемые ими следы. Но автору от этого ничуть не легче. У него есть свои пути, и он должен их придерживаться, пусть даже ему скажут (фактически), что его работа не представляет никакой ценности, недостойна опубликования и, конечно, в силу всего этого он должен прекратить присылку дальнейших работ» [22].
«Мне поручено передать Вам благодарность Королевского общества за Вашу работу «О силах, натяжениях и потоках энергии в электромагнитном поле» и сообщить Вам, что комитет по публикации статей направил эту работу для опубликования в «Philosophical Transactions». Оба рецензента, хотя и высказались благоприятно о том, что поняли, жалуются на исключительную трудность Вашей работы. Один из них назвал ее самой трудной из всех, какие он когда-либо пытался читать. Полагаете ли Вы, что Вы могли бы что-то сделать (например, добавить иллюстрации или дополнительные разъяснения), для того чтобы учесть эти замечания? Я опасаюсь, что Ваша статья, в том виде, как она есть, никому бы не принесла пользы.
Рис. 6. Джон Уильям Стратт (лорд Рэлей)
Без сомнения, в те годы, когда Хевисайд начал публикацию своих статей по развитию максвелловской электродинамики, его мало кто понимал. Уже позднее Генрих Герц писал в письме к Хевисайду:
«Это факт, что чем больше вопросов прояснилось для меня и чем больше я после этого возвращался к Вашей книге, тем больше я понимал, что, по существу. Вы уже совершили гораздо раньше то продвижение вперед, которое я думал сделать, и тем больше росло во мне уважение к Вашему труду. Но я не сразу извлекал это из Вашей книги, и другие говорили мне, что они вообще с трудом могли понять Ваши работы, поэтому я должен предупредить Вас, что Вы немного непонятны обычному человеку» [12].
Во второй фразе из приведенного отрывка Герц сетует на то, что и ему, и многим другим трудно читать Хевисайда. В одном из последующих своих писем к Хевисайду Герц снова упрекает Хевисайда за трудную для понимания манеру, в которой написаны его статьи:
«. я боюсь, что Вы до некоторой степени гордитесь тем, что непонятны для других. Я думаю, что это напрасная гордость. Вы, наверное, не знаете, до какой степени трудно другим понять Ваши работы. Людям больше нравится, когда Вы приходите к ним, чем когда они приходят к Вам, пускай даже Ваши заслуги столь велики» [12].
«В статьях был найден тот недостаток, что их было трудно читать. Но еще труднее было их писать. В журнале, где рассматриваются все разделы физики, где объем так ограничен и так ценится, сжатое изложение было крайне необходимым. Что делать исследователю, если в журналах научно-технического направления, имеющих большое число читателей, у него не принимают материал, изложенный сравнительно элементарно, а в чисто научном журнале со сравнительно небольшим числом читателей и с малым предоставляемым объемом у него не принимают тот же материал, изложенный более научно? Чтобы вообще опубликоваться, он должен сильно сжать изложение и выбросить весь объяснительный материал, какой он только может. Иначе ему могут сказать, что его статьи больше подходят для издания в виде книги и потому отклоняются» [23].
По поводу неоднократного отклонения своих статей Хевисайд заметил:
«Опыт научил меня, что если статья отвергнута журналом по неубедительным и общепринятым причинам, то это означает, что статья непривычно оригинальна и хороша. Факт!» [12].
«Засекречивание вроде того, которое практиковал Кавендиш, является абсолютно непростительным. Это грех. Можно вообразить такой случай, когда человек молчит либо от неуверенности в себе, либо от разочарования в приеме, от непризнания той работы, которую он дает миру. Мало людей имеет неограниченную силу упорства. Но делать великие открытия и хранить их в тайне, как поступил Кавендиш, без всякой уважительной причины — это, пожалуй, одно из самых больших преступлений, в которых может быть повинен такой человек. Кажется, что это сильное выражение, но поскольку, как учит нас профессор Тэт, почти преступно не знать нескольких иностранных языков, что, по мнению других, является вполне простительной бедой, то, наверное, необходимо применять сильные выражения в тех случаях, когда преступность более очевидна» [23].
- Операционное исчисление с примерами решения и образцами выполнения
- Преобразование Лапласа
- Свойства преобразования Лапласа
- Линейность
- Смещение (затухание)
- Запаздывание
- Дифференцирование оригинала
- Дифференцирование изображения
- Интегрирование оригинала
- Интегрирование изображения
- Умножение изображений
- Умножение оригиналов
- Таблица оригиналов и изображений
- Обратное преобразование Лапласа
- Формула Римана-Меллина
- Операционный метод решения линейных дифференциальных уравнений и их систем
- math4school.ru
- Оливер Хевисайд
- 1850–1925
- 🌟 Видео
Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Операционное исчисление с примерами решения и образцами выполнения
Операционное исчисление играет важную роль при решении прикладных задач, особенно в современной автоматике и телемеханике.
Операционное исчисление — один из методов математического анализа, позволяющий в ряде случаев сводить исследование дифференциальных и некоторых типов интегральных операторов и решение уравнений, содержащих эти операторы, к рассмотрению более простых алгебраических задач.
Методы операционного исчисления предполагают реализацию следующей условной схемы решения задачи.
- От искомых функций переходят к некоторым другим функциям — их изображениям.
- Над изображениями производят операции, соответствующие заданным операциям над самими функциями.
- Получив некоторый результат при действиях над изображениями, возвращаются к самим функциям.
В качестве преобразования, позволяющего перейти от функции к их изображениям, будем применять так называемое преобразование Лапласа.
Видео:7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать

Преобразование Лапласа
Оригиналы и их изображения:
Основными первоначальными понятиями операционного исчисления являются понятия функции-оригинала и функции-изображения.
Пусть f(t) — действительная функция действительного переменного t (под t будем понимать время или координату).
Функция f(t) называется оригиналом, если она удовлетворяет следующим условиям:
- f(t)— кусочно-непрерывная при
т. е. она непрерывна или имеет точки разрыва I рода, причем на каждом конечном промежутке оси t таких точек лишь конечное число.
- Существуют такие числа
что для всех t выполняется неравенство
, т. е. при возрастании t функция f(t) может возрастать не быстрее некоторой показательной функции. Число
называется показателем роста f(t).
Условия 1-3 выполняются для большинства функций, описывающих различные физические процессы.
Первое условие означает, что процесс начинается с некоторого момента времени; удобнее считать, что в момент t = 0. Третьему условию удовлетворяют ограниченные функции (для них можно положить 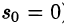
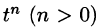
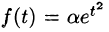
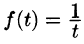
Замечание:
Функция f(t) может быть и комплексной функцией действительно переменного, т. е. иметь вид 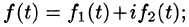
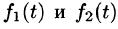
Изображением оригинала f(t) называется функция F(p) комплексного переменного 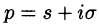
Операцию перехода от оригинала f(t) к изображению F(p) называют преобразованием Лапласа. Соответствие между оригиналом f(t) и изображением F(p) записывается в виде 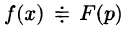
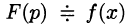
Теорема:
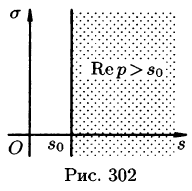
Существование изображения. Для всякого оригинала f(t) изображение F(p) существует (определено) в полуплоскости 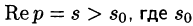
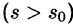
Докажем первую часть теоремы. Пусть 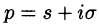
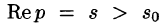
Учитывая, что 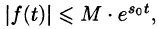
Отсюда вытекает абсолютная сходимость интеграла (78.1), т. е. изображение F(p) существует и однозначно в полуплоскости
Следствие:
Необходимый признак существования изображения. Если функция F(p) является изображением функции f(t) , то
Это утверждение непосредственно вытекает из неравенства (78.2), когда
Так как F(p) — аналитическая функция в полуплоскости
по любому направлению. Отсюда, в частности, следует, что функции 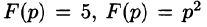
Отметим, что из аналитичности функции F(p) следует, что все ее особые точки должны лежать левее прямой 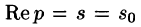
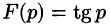
Теорема:
О единственности оригинала. Если функция F(p) служит изображением двух оригиналов 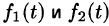
(Примем без доказательства.)
Пример:
Найти изображение единичной функции Хевисайда
Решение:
По формуле (78.1) при 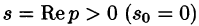
т. e. 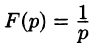
В дальнейшем функцию-оригинал будем кратко записывать в виде f(t) , подразумевал, что
Пример:
Найти изображение функции 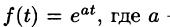
Решение:
Данная функция является оригиналом. По формуле (78.1) имеем
если Re(p — a) > 0. Таким образом,
Пример:
Найти изображение функции f(t) = t.
Решение:
В этом случае преобразование Лапласа имеет вид
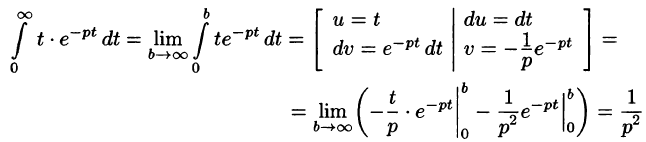
Замечание:
Функция 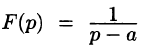
Свойства преобразования Лапласа
Находить изображения, пользуясь только определением изображения, не всегда просто и удобно. Свойства преобразования Лапласа существенно облегчают задачу нахождения изображений для большого числа разнообразных функций, а также задачу отыскания оригиналов по их изображениям.
Линейность
Линейной комбинации оригиналов соответствует такая же линейная комбинация изображений, т. е. если
— постоянные числа, то
Используя свойства интеграла, находим
Пример:
Найти изображения функций 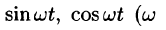
Решение:
Пользуясь свойством линейности, формулой (78.3), находим:
Аналогично получаем формулу
Далее, 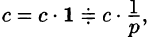
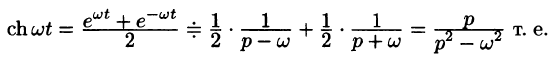
Аналогично получаем формулу
т.е. умножение аргумента оригинала на положительное число 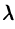
По формуле (78.1) имеем
(так как безразлично, какой буквой обозначена переменная интегрирования).
Например, пусть 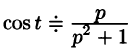
Смещение (затухание)
т. е. умножение оригинала на функцию 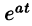
В силу формулы (78.1) имеем
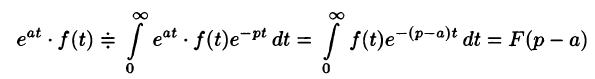
Благодаря этому свойству можно расширить таблицу соответствия между оригиналами и их изображениями:
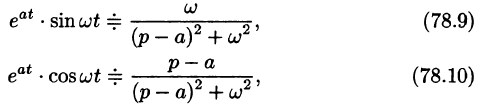
Пример:
Найти оригинал по его изображению
Решение:
Преобразуем данную дробь так, чтобы можно было воспользоваться свойством смещения:
(См. формулы (78.9), (78.10) и свойство линейности.)
Запаздывание
т. е. запаздывание оригинала на положительную величину 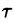
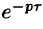
Положив 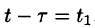
Поясним термин «запаздывание». Графики функции f(t) и 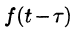
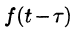
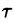
Рис. 304
Рис. 305
вправо (см. рис. 304). Следовательно, функции f(t) и 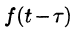
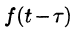
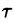
Свойство запаздывания удобно применять при отыскании изображения функций, которые на разных участках задаются различными аналитическими выражениями; функций, описывающих импульсные процессы.
называется обобщенной единично ной функцией (см. рис 305).
можно записать так:
Пример:
Найти изображение f(t) = t — 1.
Решение:
Для того чтобы быть оригиналом, функция f(t) должна удовлетворять условиям 1-3 (см. п. 78.1). В этом смысле исходную задачу можно понимать двояко.
Если понимать функцию f(t) как
т. е. 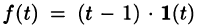
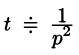
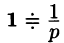
Если же понимать функцию f(t) как
т. е. 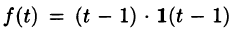
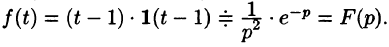
Пример:
Найти изображение функции
Решение:
Данная функция описывает единичный импульс (см. рис. 307), который можно рассматривать как разность двух оригиналов: единичной функции 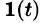
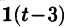
Пример:
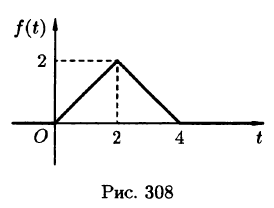
Найти изображение функции

Решение:
Функция-оригинал изображена на рис. 308. Запишем ее одним аналитическим выражением, используя функции Хевисайда 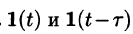
Раскроем скобки и приведем подобные слагаемые:
Изображение функции f(t) будет равно
Замечания:
1.Изображение периодического оригинала с периодом, равным Т,
есть
применяется значительно реже.
Дифференцирование оригинала
Если 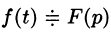
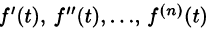
По определению изображения находим
Итак, 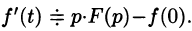
Аналогично найдем изображение третьей производной f»‘(t):
Применяя формулу (78.11) (п — 1) раз, получим формулу (78.14).
Замечание. Формулы (78.11)-(78.14) просто выглядят при нулевых начальных условиях: если
т. е. дифференцированию оригинала соответствует умножение его изображения на р.
Рассмотренное свойство дифференцирования оригинала вместе со свойством линейности широко используется при решении линейных дифференциальных уравнений.
Пример:
Найти изображение выражения
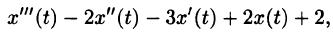
Решение:
Пусть 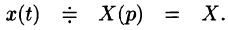
Дифференцирование изображения
Если 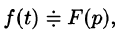
т. е. дифференцированию изображения соответствует умножение его оригинала на (-t).
Согласно теореме 78.1 существования изображения, F(p) является аналитической функцией в полуплоскости 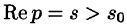
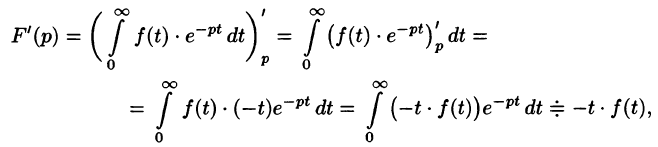
Пример:
Найти изображения функций
Решение:
Так как 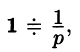
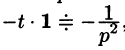
Продолжая дифференцирование, получим
С учетом свойства смещения получаем
Согласно формуле (78.5), 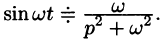
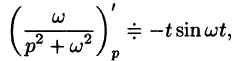
Аналогично, используя формулы (78.6), (78.7) и (78.8), находим
С учетом свойства смещения и формул (78.15) и (78.16), получаем
Интегрирование оригинала
т. е. интегрированию оригинала от 0 до t соответствует деление его изображения на р.
Функция 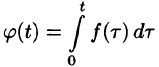
Пусть 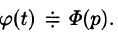
(так как 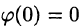
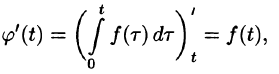
Интегрирование изображения
Если 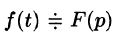
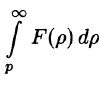
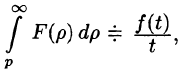
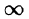
Используя формулу (78.1) и изменяя порядок интегрирования (обоснование законности этой операции опускаем), получаем
Пример:
Найти изображение функции 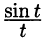
Решение:
т. е. 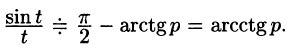
Умножение изображений
Если 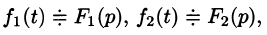
Можно показать, что функция 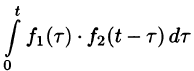
Используя преобразование Лапласа (78.1), можно записать
Область D интегрирования полученного двукратного интеграла определяется условиями 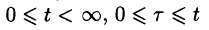
Изменяя порядок интегрирования и полагая 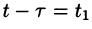
Интеграл в правой части формулы (78.17) называется сверткой функции 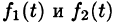
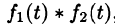
Можно убедиться (положив 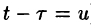
Умножение изображений соответствует свертыванию их оригиналов, т. е.
Пример:
Найти оригинал функций
Решение:
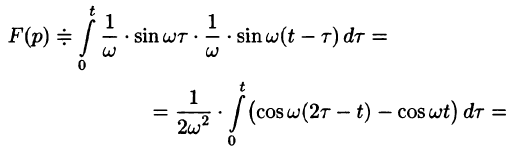
Следствие:
Если 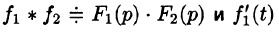
Запишем произведение 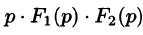
Первое слагаемое в правой части есть произведение изображений, соответствующих оригиналам 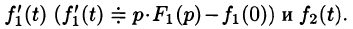
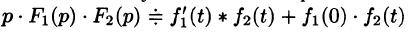
Формула (78.18) называется формулой Дюамеля. На основании свойства переместительности свертки формулу Дюамеля можно записать в виде
Формулу Дюамеля можно применять для определения оригиналов по известным изображениям.
Пример:
Найти оригинал, соответствующий изображению
Решение:
то на основании формулы Дюамеля (78.18) имеем
Умножение оригиналов
где путь интегрирования — вертикальная прямая 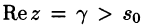
Рассмотренные свойства преобразования Лапласа представляют собой основные правила (аппарат) операционного исчисления. Для удобства пользования перечислим эти свойства.
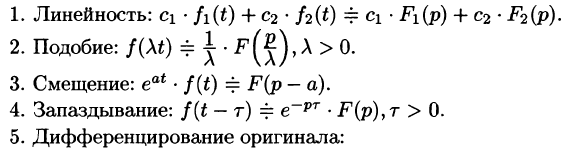
6. Дифференцирование изображения
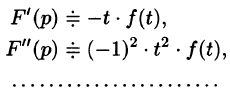
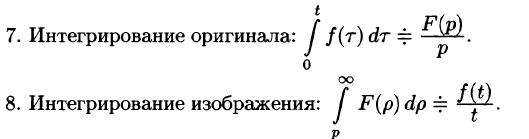
Таблица оригиналов и изображений
Составим краткую таблицу, устанавливающую соответствие между некоторыми оригиналами (часто встречающимися на практике) и их изображениями. Достаточно полная таблица оригиналов и изображений, позволяющая по заданному оригиналу находить изображение и наоборот, есть, в частности, в книге «Справочник по операционному исчислению» (авторы В. А. Диткин и П. И. Кузнецов).


Видео:Дифференциальные уравнения, 4 урок, Линейные дифференциальные уравнения первого порядкаСкачать

Обратное преобразование Лапласа
Теоремы разложения:
Рассмотрим две теоремы, называемые теоремами разложения, позволяющие по заданному изображению F(p) находить соответствующий ему оригинал f(t).
Теорема:
Если функция F(p) в окрестности точки 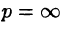
является оригиналом, имеющим изображение F(p), т. е.
Примем эту теорему без доказательства.
Пример:
Найти оригинал f(t), если
Решение:
Следовательно, на основании теоремы 79.1
Запишем лорановское разложение функции 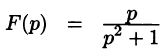
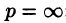
где 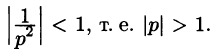
Теорема:
Если 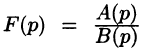
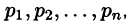
является оригиналом, имеющим изображение F(p).
Отметим, что дробь 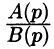
не может быть изображением.
Разложим правильную рациональную дробь 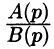
где 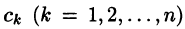
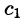
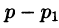
Переходя в этом равенстве к пределу при 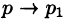
Итак, 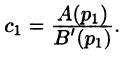
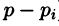
Подставляя найденные значения 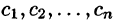
Так как по формуле (78.3)
то на основании свойства линейности имеем
Замечание:
Легко заметить, что коэффициенты 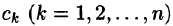
Можно показать, что если 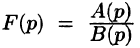
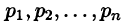
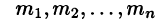
Теорему 79.2 можно сформулировать следующим образом:
Теорема:
Если изображение 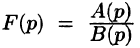
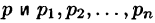
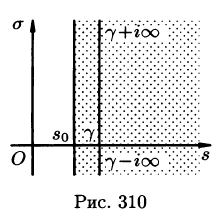
Формула Римана-Меллина
Общий способ определения оригинала по изображению дает обратное преобразование Лапласа (формула обращения Римана-Меллина), имеющее вид
где интеграл берется вдоль любой прямой 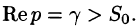
При определенных условиях интеграл (79.5) вычисляется по формуле
Замечание:
На практике отыскание функции-оригинала обычно проводят по следующему плану: прежде всего следует по таблице оригиналов и изображений попытаться отыскать для заданного изображения F(p) соответствующий ему оригинал; второй путь состоит в том, что функцию F(p) стараются представить в виде суммы простейших рациональных дробей, а затем, пользуясь свойством линейности, найти оригинал; наконец, использовать теоремы разложения, свойство умножения изображений, формулу обращения и т.д.
Пример:
Найти оригинал по его изображению
Решение:
Проще всего поступить так:
(использовали свойство линейности и формулы (78.5) и (78.6)).
Если же использовать теорему 79.2 разложения, то будем иметь:
корни знаменателя 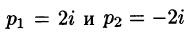
Пример:
Найти функцию-оригинал, если ее изображение
задано как
Решение:
— простой корень знаменателя, 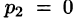
Приведем другой способ нахождения f(t). Разобьем дробь
на сумму простейших дробей:
Приведем третий способ нахождения f(t). Представим F(p) как
произведение 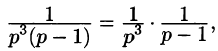
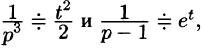
Операционный метод решения линейных дифференциальных уравнений и их систем
Пусть требуется найти частное решение линейного дифференциального уравнения с постоянными коэффициентами
удовлетворяющее начальным условиям
где 
Будем считать, что искомая функция y(t) вместе с ее рассматриваемыми производными и функция f(t) являются оригиналами.
Пусть 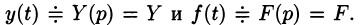
Полученное уравнение называют операторным (или уравнением в изображениях). Разрешим его относительно Y:
— алгебраические многочлены от p степени п и п-1 соответственно. Из последнего уравнения находим
Полученное равенство называют операторным решением дифференциального уравнения (80.1). Оно имеет более простой вид, если все начальные условия равны нулю, т. е.
В этом случае
Находя оригинал y(t), соответствующий найденному изображению (80.2), получаем, в силу теоремы единственности, частное решение дифференциального уравнения (80.1).
Замечание:
Полученное решение y(t) во многих случаях оказывается справедливым при всех значениях t (а не только при 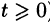
Пример:
Решить операционным методом дифференциальное уравнение 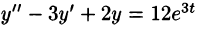
Решение:
Пусть 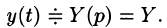
Подставляя эти выражения в дифференциальное уравнение, получаем операторное уравнение:
Отсюда 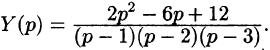
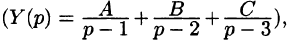
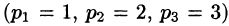
Пример:
Найти решение уравнения
при условии
Решение:
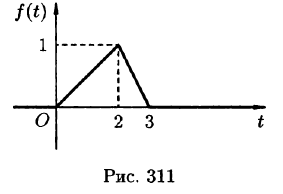
График данной функции имеет вид, изображенный на рисунке 311.
С помощью единичной функции правую часть данного дифференциального уравнения можно записать одним аналитическим выражением:
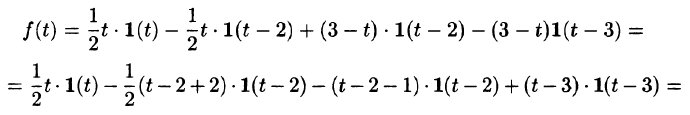
Таким образом, имеем
Операторное уравнение, при нулевых начальных условиях имеет вид
то по теореме запаздывания находим:
Аналогично применяется операционный метод для решения систем линейных дифференциальных уравнений с постоянными коэффициентами.
Покажем это на конкретном примере.
Пример:
Решить систему дифференциальных уравнений
Решение:
Система операторных уравнений принимает вид
Решая эту систему алгебраических уравнений, находим:
Переходя от изображений к оригиналам, получаем искомые решения:
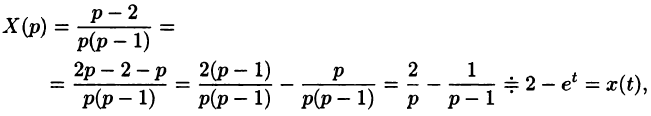
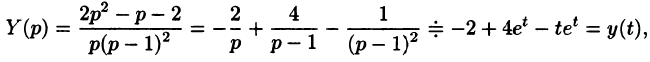
С помощью операционного исчисления можно также находить решения линейных дифференциальных уравнений с переменными коэффициентами, уравнений в частных производных, уравнений в конечных разностях (разностных уравнений); производить суммирование рядов; вычислять интегралы. При этом решение этих и других задач значительно упрощается.
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Видео:16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать

math4school.ru
Видео:Математика без Ху!ни. Линейное неоднородное уравнение 1 порядка. Метод вариации постоянной.Скачать

Оливер Хевисайд
1850–1925
Почетно иметь такого предшественника.
Илья Михайлович Франк
Оливер Хевисайд (18 мая 1850 – 3 февраля 1925) – английский учёный-самоучка, инженер, математик и физик. Хевисайд большую часть жизни был не в ладах с научным сообществом, но его работы изменили облик математики и физики.
Хевисайд родился в Англии, лондонском районе Кэмден, в семье Томаса Хевисайда и Рейчел Элизабет Вест и был младшим из их четырёх сыновей. Отец работал гравером и художником. В раннем детстве Оливер переболел скарлатиной, в результате чего серьёзно пострадал его слух, и он был слабослышащим всю оставшуюся жизнь. Это обстоятельство серьёзно повлияло на его детство, так как из-за проблем со слухом он не мог нормально общаться с ровесниками.
В детстве Оливер неплохо рисовал, о чем свидетельствуют рисунки, сделанные им в 11-летнем возрасте. Возможно, что отец собирался обучить его своему искусству, но интересы Оливера вскоре обратились от искусства к науке об электричестве. Трудно сказать, что повлияло на этот выбор. Есть, впрочем, одно вероятное объяснение. Его тетка по матери была женой Чарлза Уитстона, известного физика, автора многих исследований по акустике, оптике, электричеству и магнетизму.
Семья была не очень состоятельная, поэтому Оливер смог закончить только неполную среднюю школу – так неточно мы переводим elementary school, общедоступную школу, где обучались дети до 14 – 15 лет.
Хевисайд учился в школе очень хорошо. После её окончания он был пятым из более чем 500 претендентов на сдачу экзамена в колледж в 1865 году.
Самой плохой оценкой будущего корифея в области математической физики был 15%-ный бал по евклидовой геометрии — любопытное обстоятельство, явившееся одним из первых проявлений неприязни Хевисайда к «строгим доказательствам». Учёный впоследствии писал:
Самое худшее – это евклидова геометрия. Поразительно, что молодые люди должны забивать себе голову всякими логическими вывертами и пытаться понять доказательство одного очевидного факта посредством другого, в равной степени. очевидного, ощущая в себе зарождающуюся неприязнь к математике, вместо того, чтобы изучать геометрию, один из наиболее важных и фундаментальных предметов.
Молодой Хевисайд, не имея ни средств, ни желания получить дальнейшее академическое образование, в шестнадцатилетнем возрасте оставил стены учебного заведения, самостоятельно выучил азбуку Морзе, основы электричества, немецкий и датский языки и в возрасте 18 лет отправился в Данию, где устроился работать в телеграфной компании. Это была его единственная оплачиваемая работа. Хевисайд освоил специальность телеграфиста и наладчика телеграфных аппаратов и быстро продвигался по службе.
В 1871 году он вернулся в Англию и стал главным оператором в бюро телеграфной компании Great Northern Telegraph, которое находилось в городе Ньюкасл и ведало международным телеграфом. В то же время он усиленно занимался самообразованием, делая упор на математику. Первыми вехами на научном пути Хевисайда стали две его статьи по электричеству, опубликованные в 1872 и 1873 годах. В первой статье использовалась только алгебра, тогда как во второй, которую отметил Максвелл во втором издании своего «Трактата об электричестве и магнетизме», был применен математический анализ. Внимание Максвелла вдохновляет Хевисайда на более серьёзные занятия наукой.
В 1874 году он оставляет должность телеграфиста и занимается исследованиями частным порядком в доме своих родителей.
Возможно, что под впечатлением от замечательного трактата Максвелла Хевисайд принял решение оставить телеграфную компанию, чтобы полностью посвятить себя научной работе. Это был весьма серьезный шаг для двадцатичетырехлетнего человека, не имевшего независимых средств к существованию. Хевисайд никогда не пытался пересмотреть свое решение оставить работу в столь раннем возрасте. Это весьма тревожило его семью, хотя все в ней отнеслись с участием к его намерениям и старались не досаждать ему – даже поднос с едой оставляли у дверей его комнаты, ставни которой обычно были плотно закрыты. В этой комнате Хевисайд проводил за работой все ночи и значительную часть дня при свете коптящих масляных ламп, от которых, по словам знакомого Хевисайда, в комнате становилось «жарче, чем в аду».
Хевисайда (как и молодого Эйнштейна 25 лет спустя) математическая физика привлекла своей внутренней простотой и изяществом, характерными даже для таких сложных построений, как уравнения Максвелла. Максвелл продемонстрировал единство электричества и магнетизма, придав математическую форму представлениям Фарадея о двух силах как о полях. Система уравнений Максвелла позволила объяснить многие известные явления и предсказать те, о которых даже не подозревали. Наиболее же важным был вывод Максвелла о том, что колеблющееся электрическое поле должно порождать в пространстве магнитное поле, колеблющееся с той же частотой, которое в свою очередь должно порождать электрическое поле и т.д. Эта электромагнитная волна должна распространяться со скоростью света, также являющегося электромагнитным излучением.
Максвелл умер в 1879 году в возрасте 48 лет, за девять лет до того как гениальный немецкий ученый Генрих Герц экспериментально доказал существование электромагнитных волн в пространстве.
Хевисайду не нужны были подтверждения электромагнитной теории Максвелла, поскольку он считал ее «очевидной истиной» уже в силу ее одной математической структуры. Создать такое, по словам Хевисайда, мог только «божественный гений». О том, сколь большое впечатление на Хевисайда произвела работа Максвелла «Трактат об электричестве и магнетизме», можно судить по его письму, написанному в 1918 году
Я увидел, что она [теория] обладает великой, величайшей и удивительной по своим возможностям силой. Я был полон решимости овладеть ею и принялся за работу. Мне потребовалось несколько лет, прежде чем я постиг то, что мог. Затем я отложил труд Максвелла в сторону и пошел своим путем. И продвигался уже гораздо быстрее.
В 1880 году Хевисайд исследовал скин-эффект в телеграфных линиях передачи и переписал результаты Максвелла из их первоначальной формы к форме, выраженной в терминах современного векторного анализа, таким образом, сведя систему из 20 уравнений с 12 переменными к 4 дифференциальным уравнениям, известным как уравнения Максвелла. Четыре уравнения Максвелла описывают природу неподвижных и движущихся заряженных частиц и магнитных диполей, и отношения между ними, а именно электромагнитную индукцию.
В 1887 году Хевисайд предложил добавить катушки индуктивности к трансатлантическому телеграфному кабелю (увеличив тем самым собственную индуктивность) для коррекции возникавших искажений. По политическим причинам этого сделано не было. Позднее, сербский физик Михайло Пупин разработал способ увеличения дальности передачи для телефонных линий с помощью установки удлинительных катушек через определённые интервалы вдоль линии передачи. Этот метод следовал идеям Хевисайда.
В двух работах 1888 года и 1889 года Хевисайд вычислил деформацию электрического и магнитного полей вокруг движущегося заряда, а также эффекты вхождения заряда в плотную среду. Он предсказал излучение Вавилова – Черенкова и вдохновил Джорджа Фитцджеральда предложить понятие так называемого сокращения Лоренца – Фитцджеральда.
В 1889 году, после открытия Томсоном электрона, Хевисайд начал работу над концепцией электромагнитной массы. Хевисайд считал её настолько же настоящей, как и массу материальную, способной производить такие же эффекты. Вильгельм Вин позднее проверил результат Хевисайда для малых ускорений.
Блестящие успехи Хевисайда в развитии теории Максвелла не остались незамеченными. Хотя большинство своих работ он публиковал в журнале Electrician («Электрик»), рассчитанном на инженеров-электриков, этот журнал читали и многие известные ученые. Даже великий Максвелл когда-то опубликовал в нем свою заметку. Поэтому научная элита была вполне осведомлена о том, что представлял собой Хевисайд как ученый.
Методы Хевисайда были столь же важны, как и его результаты. Вместе с Джозайя Уиллардом Гиббсом из Иельского университета Хевисайд научил физиков мира, как оперировать векторами. Векторы позволяют описывать силы, характеризуемые численным значением и направлением. Если один вектор представляет силу в данной точке, то система векторов – силовое поле. Над векторами могут выполняться арифметические действия, а также дифференциальные операции; путем дифференцирования системы векторов, описывающей, например, магнитное поле, находится вектор электрического потока в любой данной точке. Фактически, Хевисайд стал отцом векторного анализа.
Вторым вкладом Хевисайда в математику стало создание операционного исчисления (1880–1889). Он разработал новый эффективный метод решения линейных дифференциальных уравнений. В этом методе операция дифференцирования по одной из переменных заменяется умножением дифференцируемой функции на некоторый символ (Хевисайд ввёл обозначение D для дифференциального оператора), который до поры до времени может рассматриваться как простое число. Такая замена упрощает уравнение, а если искомая функция зависит только от одной переменной, то дифференциальное уравнение превращается в алгебраическое. Затем упрощенное уравнение решается обычными методами, а в полученном выражении символ, заменяющий операцию дифференцирования, вновь обретает свой первоначальный смысл. Таким образом, решение является некоторым оператором, который нужно применить к заданной функции, чтобы получить решение в явном виде. Хевисайд показал, что для большого класса физически важных задач получение решения таким методом сводится к выполнению ряда стандартных операций, которые и были им выполнены.
Операционное исчисление получило широкое применение при решении целого ряда задач в различных областях физики: в теории теплопроводности и диффузии, при изучении электрических цепей и линий связи, в задачах распространения радиоволн. Удобство этого метода, помимо стандартности вычисления, состоит в том, что таким способом можно эффективно рассматривать процессы установления, или, как говорят, переходные процессы.
Метод решения дифференциальных уравнений с помощью сведения к обыкновенным алгебраическим уравнениям, поначалу вызвал бурную полемику из-за отсутствия строгого обоснования. Тогда Хевисайд произнёс известную фразу:
Математика есть наука экспериментальная, определения появляются последними.
Это было ответом на критику за использование ещё не вполне определённых операторов.
Хевисайд широко использовал в своих расчетах еще одну функцию. Он назвал ее импульсной. Эта функция обладала очень странными свойствами. Она равнялась нулю во всех точках, кроме одной, где она обращалась в бесконечность таким образом, что интеграл от этой функции равнялся единице, если эта точка попадала в промежуток интегрирования. Эта функция описывает импульсное воздействие на систему.
Такое воздействие имеет место, например, при упругом соударении двух жестких шаров. Силы действуют на шары только в момент соударения, а интеграл от силы по времени, т.е. переданный при соударении импульс, отличен от пуля. Импульсная функция определяет также плотность точечного источника. Хевисайд подробно разобрал свойства этой функции. Однако эти работы Хевисайда были забыты. Больше чем через тридцать лет эту функцию заново ввел в физику Дирак. Теперь импульсная функция Хевисайда часто применяется в теоретической физике и носит название дельта-функции Дирака.
Работы Хевисайда по операционному исчислению первоначально не получили признания математиков. Почему так произошло?
Хевисайд был самоучка. Он не учился в университете (и даже в средней школе последней ступени), не слушал лекций, не посещал семинарских занятий, т.е. не прошел того пути, на котором было воспитано подавляющее большинство английских ученых. Все свои знания он добыл без помощи преподавателей. Но обучение в университете давало не только научные знания. Обучение было одновременно и воспитанием в духе научных традиций, и введением в научное сообщество. Человек, окончивший Кембриджский или Оксфордский университет, уже в силу только этого факта мог рассчитывать на внимательное отношение к себе и к своим научным результатам со стороны многих и многих ученых, прошедших ту же школу, тот же путь научного воспитания. Если научные результаты не вызывали сомнения, они получали безоговорочную поддержку, если результаты вызывали возражения, автор мог рассчитывать на доброжелательную критику. Он был равноправным членом научного сообщества.
Хевисайд не вошел в научное сообщество, как теперь говорят, «не вписался». Его подход к проблеме был нетрадиционным, непривычным для членов научного сообщества и столь же непривычной была манера изложения полученных результатов. Занимаясь в полном уединении, он выработал свой стиль выбора и рассмотрения научной проблемы, и этот стиль был в некоторых отношениях далек от традиционного. Он создал свой язык и свою систему образов в науке, и они тоже отличались от традиционных.
Непринятие математиками стиля Хевисайда в значительной мере затрудняло публикацию его работ (потому что строгие математики были в числе рецензентов, н можно думать, что они писали отрицательные рецензии на посланные в печать статьи Хевисайда), а также вело к явной недооценке уже опубликованных его работ.
Хевисайд неоднократно выражал свое отношение к требованию математической строгости на самом высшем уровне при изложении физических теорий. Он, в частности, писал:
Нужно по возможности полнее избегать вошедшего в обычай избавления от физики путем сведения задачи к чисто математическому упражнению. Следует все время не упускать из вида физику, чтобы придать задаче жизнь и реальное значение и чтобы получить большую помощь, которую физика дает математике. Это не всегда может быть сделано, особенно в деталях, которые требуют больших вычислений, но этот общий принцип следует проводить в жизнь по возможности полнее, уделяя особое внимание движущим идеям. Ни один математический пурист никогда бы не смог выполнить работу, заключенную в максвелловском трактате. Он мог бы знать всю необходимую математику и даже больше, но это не привело бы к цели, потому что он не смог бы сложить все вместе без физического руководства. Это обстоятельство ни в коей мере его не позорит, но только показывает различие в путях мышления. За последние полвека чистая математика достигла огромных успехов, и было бы правильной справедливо поставить их в соответствие с успехами в физической науке. Но вместе с тем к пуристам пришла склонность возражать против введения физических идей в математику с возможной в результате потерей строгости. Может оказаться, что иногда не только не происходит потери строгости, но увеличивается общность и упрощается рассмотрение.
Хевисайд не отрицал, что применяемые им математические методы еще не имели в то время строгого обоснования. Но он считал, что если метод доказал свою эффективность, то нужно этот метод применять, не дожидаясь строгого обоснования. Он приводит в пример введенные им операторы сопротивления электрической цепи
Действительно, их использование часто ведет к большим упрощениям и избавляет от необходимости проводить сложные вычисления определенных интегралов. Но при этом строгая логика дела не ясна! Ну и что из того? Буду ли я отказываться от обеда потому, что не понимаю полностью процесс пищеварения? Нет, не буду, если я удовлетворен результатом. Подобным образом и физик может применять нестрогие процессы с удовлетворением и пользой, если он, проводя проверки, убеждается в точности своих результатов.
Хевисайд утверждал, что успехи математики связаны с успехами физической науки. Строгая математическая физика времен Хевисайда, в конечном счете, уходит корнями в ньютоновскую механику. Те, кто упрекал Хевисайда в математической нестрогости, не понимали, что наступает время новой физики, которая не сводится к ньютоновской механике. А новая физика требовала новой математики, и Хевисайд это понимал. В частности, когда его упрекали за применение расходящихся рядов, которые тогда не рассматривались в теории функций, он отвечал:
А как насчет теории функций, которая сознательно отказывается от рассмотрения расходящихся рядов? Может ли она действительно быть теорией функций? Разве не нужна теория с большим охватом, объединяющая и сходящиеся и расходящиеся ряды в единое гармоническое целое?
В 1891 году Хевисайд был избран членом Лондонского королевского общества, причем его кандидатуру поддержали такие знаменитости как Томсон, Лодж, Фицджеральд и Пойнтинг. Звание члена Лондонского королевского общества, очень престижное и сегодня, в те времена, когда еще не были учреждены различные премии ученым, считалось еще более почетным. Таким образом, за 17 лет Хевисайд из безвестного безработного телеграфиста превратился в мировую известность.
В 1905 году Хевисайд стал почётным доктором Университета Гёттингена.
В 1918 году Хевисайд был избран почетным членом Американского института инженеров-электриков.
В 1921 году Институт инженеров-электриков основал медаль Фарадея в память н в честь этого великого ученого. Первая медаль Фарадея был присуждена Хевисайду.
Все почетные отличия никак не облегчали жизнь Хевисайда. Он получает пенсию в 220 фунтов в год. До войны он мог прожить на эти деньги, но после войны цены поднялись, а пенсия не выросла. Хевисайд сначала испытывал материальные затруднения, а потом узнал реальную нужду.
Будучи всю жизнь не в ладах с научным сообществом, в последние годы жизни учёный стал особенно эксцентричен. Он любил тепло и расточительно пользовался газом, поэтому у него были испорчены отношения с газовой компанией, а также со сборщиком платы за газ. Хевисайд был полон негодования против «газовых варваров», как он называл газовую компанию, и его негодование распространялось и на сборщика платы за газ. Когда тот приходил, Оливер впускал его в дом, запирал входную дверь, клал ключ в карман, вводил сборщика в свой рабочий кабинет и запирал дверь кабинета тоже. Потом следовали долгие переговоры, после которых сборщик всегда уходил без д:нег. Однажды полиция описала его мебель, и дело шло к распродаже, но банк дал ему некоторую ссуду, и распродажа не состоялась.
В этот период Хевисайд подписывал корреспонденцию своим именем с инициалами W.O.R.M. Слово «worm» переводится с английского как «червяк», но способ, которым Хевисайд писал это слово – заглавными буквами, с точкой после каждой буквы – о многом говорил.
Дело в том, что у англичан (да и не только у них) человек, подписывая официальное письмо, после своей подписи нередко перечисляет свои чины и звания, причем англичанин использует для этого сокращения, например: М.P. (Member of Parliament) – член парламента, D.М. (Doctor of Medicine) – доктор медицины, F.R.S. (Fellow of The Royal Society) – член Королевского общества, К.С.В. (Knight Commander of The Bath) – кавалер ордена Бани 2-й степени и т.д. Хевисайду этот обычай не нравился. При желании он и сам мог подписываться так: О. Хевисайд, F.R.S., Ноn.М.I.Е.Е. (что означало: член Королевского общества, почетный член Института инженеров-электриков). Но он считал это смешным. Вот он и выбрал слово «worm», выписывая его после подписи заглавными буквами и ставя точку после каждой буквы.
Хотя в молодости Хевисайд активно занимался велосипедным спортом, с возрастом его здоровье серьёзно ухудшилось.
Умер Хевисайд 3 февраля 1925 года, вероятно, вследствие ушибов, которые он получил, упав с лестницы за несколько месяцев до своей кончины. Похоронен на кладбище Пейнтон.
О смерти Хевисайда было сообщено по радио. В некоторых научных и технических журналах появились краткие сообщения и памятные статьи, посвященные Хевисайду. Мало кто лично знал Хевисайда, да и те, кто его знал, по большей части мало что могли сказать о его жизни. Не знали даже его возраста.
Хевисайду принадлежит приоритет в следующих научных открытиях:
- создание векторного анализа;
- создание операционного исчисления (теория преобразований Лапласа);
- создание операторного метода для линейных дифференциальных уравнений;
- применение комплексных чисел для изучения электрических цепей;
- упрощение 20 уравнений Максвелла с 12 переменными и сведение их к 4 уравнениям с двумя переменными – векторами электрического и магнитного поля. Независимо это проделал и Герц. В течение ряда лет уравнения электродинамики в новой форме назывались уравнениями Герца–Хевисайда, молодой Эйнштейн называл их уравнениями Максвелла–Герца, а сегодня эти уравнения носят имя только Максвелла;
- в 1890 году, за пятнадцать лет до Эйнштейна, Хевисайд получил знаменитую формулу E=mc 2 ;
- предсказал наличие особого слоя озона у атмосферы (ионосферы), благодаря этому возможна сверхдальняя радиосвязь;
- предсказание в 1895 году излучения Вавилова–Черенкова. Последнему в 1958 году была присуждена Нобелевская премия (вместе еще с двумя советскими теоретиками И.Е. Таммом и И.М. Франком);
- ввел в физику дельта-функцию (функция Дирака);
- на тридцать лет раньше Дирака обосновал магнитный монополь.
Имя Хевисайда носят следующие объекты естествознания:
- функция Хевисайда
- слой Кенелли–Хевисайда
- условия Хевисайда
- теорема разложения Хевисайда.
🌟 Видео
Решение системы дифференциальных уравнений методом ЭйлераСкачать

9. Метод вариации произвольной постоянной ( метод Лагранжа ). Линейные дифференциальные уравнения.Скачать

Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Как распознать талантливого математикаСкачать

Метод Лагранжа & Метод Бернулли ★ Решение линейных неоднородных дифференциальных уравненийСкачать

Линейное дифференциальное уравнение Коши-ЭйлераСкачать

Как решать Диофантовы уравнения ★ 9x+13y=-1 ★ Решите уравнение в целых числахСкачать

19. Метод вариации произвольных постоянных. Линейные неоднородные диф уравнения 2-го порядкаСкачать

Дифференциальные уравнения, 8 урок, Линейные дифференциальные уравнения с const коэф-ами 2 порядкаСкачать

#Дифуры I. Урок 4. Линейные дифференциальные уравнения. Метод вариации произвольной постояннойСкачать

Линейное однородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами.Скачать

Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами 4y''-y=x^3-24x #1Скачать

Дифференциальные уравнения, 5 урок, Уравнение БернуллиСкачать


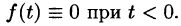
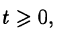 т. е. она непрерывна или имеет точки разрыва I рода, причем на каждом конечном промежутке оси t таких точек лишь конечное число.
т. е. она непрерывна или имеет точки разрыва I рода, причем на каждом конечном промежутке оси t таких точек лишь конечное число.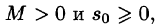 что для всех t выполняется неравенство
что для всех t выполняется неравенство 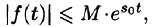 , т. е. при возрастании t функция f(t) может возрастать не быстрее некоторой показательной функции. Число
, т. е. при возрастании t функция f(t) может возрастать не быстрее некоторой показательной функции. Число 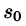 называется показателем роста f(t).
называется показателем роста f(t).