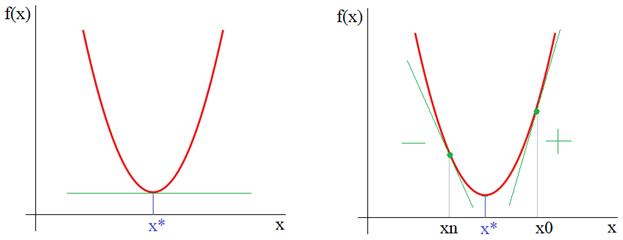
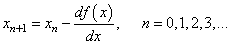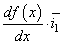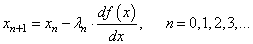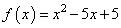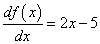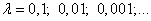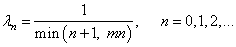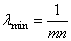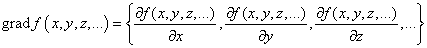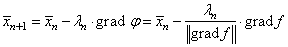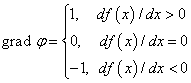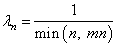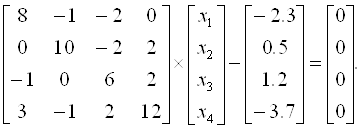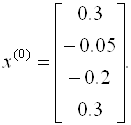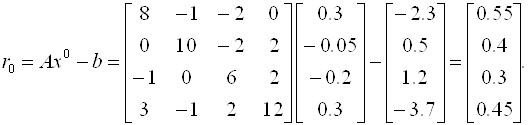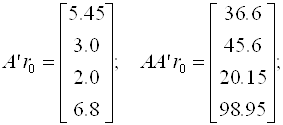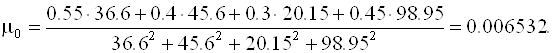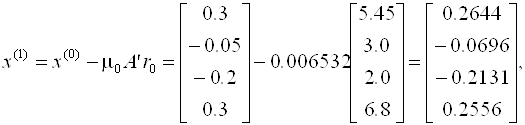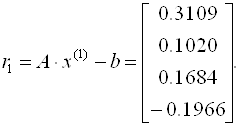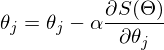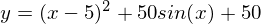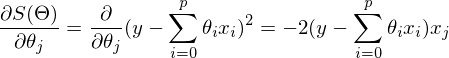Метод градиентного спуска решение уравнений (3 видео)

Метод градиентного спуска

На этом занятии мы с вами рассмотрим довольно популярный алгоритм под названием «метод градиентного спуска» или, еще говорят «метод наискорейшего спуска». Идея метода довольно проста. Предположим, имеется дифференцируемая функция 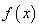с точкой экстремума x*. Нам нужно найти эту точку. Для простоты восприятия информации, предположим, что это парабола с точкой экстремума x*. Конечно, для такого простого случая эту точку можно очень легко определить из уравнения:

но она используется лишь для визуализации метода градиентного спуска. В действительности функции могут быть гораздо сложнее и зависеть от произвольного числа аргументов, для которых решать системы уравнений достаточно хлопотное занятие. Или же, функция постоянно меняется и нам необходимо под нее подстраиваться для определения текущего положения точки минимума. Все эти задачи удобнее решать с позиции алгоритмов направленного поиска, например, градиентного спуска.

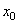
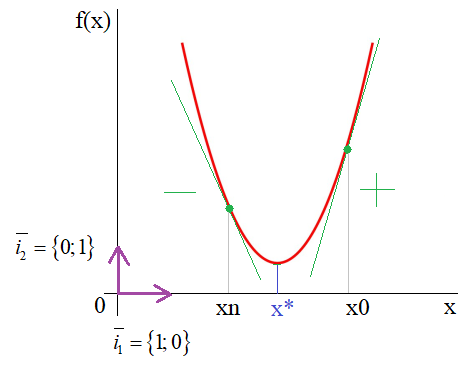
Итак, из рисунка мы хорошо видим, что справа от точки экстремума x* производная положительна, а слева – отрицательна. И это общее математическое правило для точек локального минимума. Предположим, что мы выбираем произвольную начальную точку на оси абсцисс. Теперь, смотрите, чтобы из двигаться в сторону x*, нам нужно в области положительных производных ее уменьшать, а в области отрицательных – увеличивать. Математически это можно записать так:

Здесь n – номер итерации работы алгоритма. Но, вы можете спросить: а где же тут градиент? В действительности, мы его уже учли чисто интуитивно, когда определяли перемещение вдоль оси абсцисс для поиска оптимальной точки x*. Но математика не терпит такой вульгарности, в ней все должно быть прописано и точно определено. Как раз для этого нужно брать не просто производную, а еще и определять направление движения, используя единичные векторы декартовой системы координат:

И градиент функции 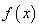можно записать как

то есть, это будет уже направление вдоль оси ординат и направлен в сторону наибольшего увеличения функции. Соответственно, двигаясь в противоположную сторону, будем перемещаться к точке минимума x*.

Конечно, в результирующей формуле алгоритма поиска этот единичный вектор не пишется, а вместо него указывается разность по оси ординат, т.к. именно вдоль нее он и направлен:

Однако у такой формулы есть один существенный недостаток: значение производной может быть очень большим и мы попросту «перескочим» через значение x* и уйдем далеко влево или вправо. Чтобы этого не происходило, производную дополнительно умножают на некоторое небольшое число λ:

которое, в общем случае, также может меняться от итерации к итерации. Этот множитель получил название шаг сходимости.

Давайте, для примера, реализуем этот алгоритм на Python для случая одномерной параболы. Вначале подключим необходимые библиотеки и определим две функции: параболу

и ее производную:

Затем, определим необходимые параметры алгоритма и сформируем массивы значений по осям абсцисс и ординат:

Далее, переходим в интерактивный режим работы с графиком, чтобы создать анимацию для перемещения точки поиска минимума и создаем окно с осями графика:

Отображаем начальный график:

Запускаем алгоритм градиентного поиска:

В конце выводим найденное значение аргумента и оставляем график на экране устройства:

После запуска увидим скатывание точки к экстремуму функции. Установим значение

Увидим «перескоки» оптимального значение, то есть, неравномерную сходимость к точки минимума. А вот, если поставить параметр

то скатывания совсем не будет, т.к. аргумент x будет «перескакивать» точку минимума и никогда ее не достигать. Вот так параметр λ влияет на работу алгоритма градиентного спуска.

Содержание

Выбор шага сходимости
Локальный минимум
Видео по теме
3.8. Метод скорейшего спуска (градиента) для случая . системы линейных алгебраических уравнений
Математика для искусственных нейронных сетей для новичков, часть 2 — градиентный спуск
Градиентный спуск
📸 Видео

Видео:ЦОС Python #2: Метод градиентного спускаСкачать

Выбор шага сходимости

Важно правильно его подбирать в каждой конкретной решаемой задаче. Обычно, это делается с позиции «здравого смысла» и опыта разработчика, но общие рекомендации такие: начинать со значения 0,1 и уменьшать каждый раз на порядок для выбора лучшего,

который обеспечивает и скорость и точность подбора аргумента x. В целом, это элемент творчества и, например, можно встретить и такой вариант изменения шага сходимости:

Функция min здесь выбирает наименьшее из двух аргументов и использует его в знаменателе дроби. Это необходимо, чтобы величина шага при больших n не становилась слишком маленькой и ограничивалась величиной

где mn – некоторое заданное ограничивающее значение.

Еще один прием связан с нормализацией градиента на каждом шаге работы алгоритма. В этом случае градиент функции (то есть, вектор):

приводится к единичной норме:

И уже он используется в алгоритме наискорейшего спуска:

В одномерном случае нашего примера, это, фактически означает, что вместо действительного значения градиента, берутся числа ±1:

И алгоритм в Python примет вид:

Как видите, такой подход требует уменьшения величины шага сходимости, на последующих итерациях, например, так:

Результат выглядит уже лучше и при этом, мы не привязаны к значению градиента.

Видео:Градиентный метод | метод скорейшего спуска + примерСкачать

Локальный минимум

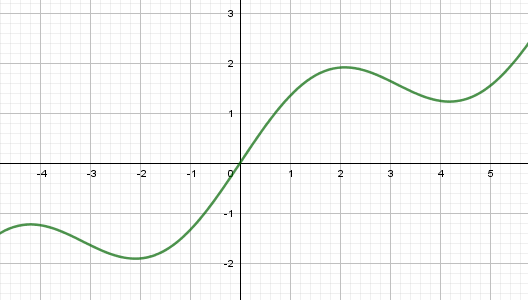
Еще одной особенностью работы этого алгоритма является попадание в область локального минимума функции. Например, если взять вот такой график:

То при начальном значении x=0 получим один минимум, а, например, при x=2,5 – другой. В этом легко убедиться, если в нашей программе переписать функции:

(последняя – это производная: ). Увеличим диапазон отображения графика:

и запустим программу. Теперь, установим начальное значение xx=2,5, снова запустим и увидим уже другую точку локального минимума.

Это, наверное, основной недостаток данного алгоритма – попадание в локальный минимум. Чтобы решить эту проблему перебирают несколько разных начальных значений и смотрят: при котором был достигнуто наименьшее значение. Его и отбирают в качестве результата. Такой ход не дает нам гарантии, что действительно был найден глобальный минимум функции (иногда он может не существовать, как, например, с нашей синусоидой), но, тем не менее, это повышает наш шанс найти лучшее решение. Вот базовая теория и практика применения метода наискорейшего спуска.

Видео по теме

#1: Метод наименьших квадратов

#2: Метод градиентного спуска

#3: Метод градиентного спуска для двух параметров

#4: Марковские процессы в дискретном времени

#5: Фильтр Калмана дискретного времени

#6: Фильтр Калмана для авторегрессионого уравнения

#7: Векторный фильтр Калмана

#8: Фильтр Винера

#9: Байесовское построение оценок, метод максимального правдоподобия

#10: Байесовский классификатор, отношение правдоподобия

© 2022 Частичное или полное копирование информации с данного сайта для распространения на других ресурсах, в том числе и бумажных, строго запрещено. Все тексты и изображения являются собственностью сайта

Видео:ЦОС Python #3: Метод градиентного спуска для двух параметровСкачать

3.8. Метод скорейшего спуска (градиента) для случая . системы линейных алгебраических уравнений

В рассматриваемом ниже итерационном методе вычислительный алгоритм строится таким образом, чтобы обеспечить минимальную погрешность на шаге (максимально приблизиться к корню).

Представим систему линейных уравнений в следующем виде:

(3.38)

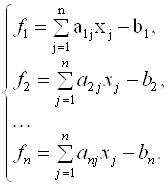
Запишем выражение (3.38) в операторной форме:

(3.39)

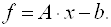
Здесь приняты следующие обозначения:

; ; . (3.40)

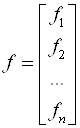
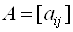
В методе скорейшего спуска решение ищут в виде

, (3.41)

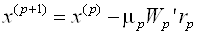
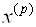
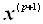
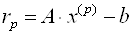
Где и — векторы неизвестных на 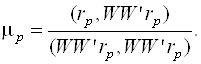P и P+1 шагах итераций; вектор невязок на P-ом шаге определяется выражением

, (3.42)

А (3.43)

В формуле (3.43) используется скалярное произведение двух векторов, которое определяется следующей формулой:

(3.44)

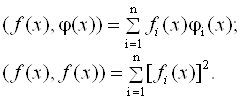
В формуле (3.43) 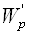— транспонированная матрица Якоби, вычисленная на P-ом шаге. Матрица Якоби вектор – функции F(X) определяется как

(3.45)

Нетрудно убедиться, что для системы (3.39) матрица Якоби равна

(3.46)

Как и для метода простой итерации, достаточным условием сходимости метода градиента является преобладание диагональных элементов. В качестве нулевого приближения можно взять .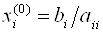

· Как видно из выражения (3.45), матрица Якоби не зависит от шага итерации.

· Требования минимизации погрешности на каждом шаге обусловили то, что метод градиента более сложен (трудоемок), чем методы Якоби и Зейделя.

· В методе градиента итерационный процесс естественно закончить при достижении 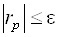, вектор невязок входит в вычислительную формулу.

· В приближенных методах можно обеспечить практически любую погрешность, если итерационный процесс сходится.

· Итерационный процесс можно прервать на любом K–ом шаге и продолжить позднее, введя в качестве нулевого шага значения X(K).

· В качестве недостатка приближенных методов можно отметить то, что они часто расходятся, достаточные условия сходимости (преобладание диагональных элементов) можно обеспечить только для небольших систем из 3 – 6 уравнений.

Пример 3.7. Методом скорейшего спуска решим систему уравнений

Так как диагональные элементы матрицы являются преобладающими, то в качестве начального приближения выберем:

Следовательно, вектор невязок на нулевом шаге равен

Далее последовательно вычисляем

Отсюда

Аналогично находятся последующие приближения и оцениваются невязки. Что касается данного примера, можно отметить, что итерационный процесс сходится достаточно медленно (невязки уменьшаются).

Вопросы для самопроверки

· Назовите известные вам методы решения СЛАУ.

· Чем точные методы отличаются от приближенных?

· Что такое прямой и обратный ход в методе Гаусса?

· Нужен ли обратный ход при вычислении методом Гаусса а) обратной матрицы; б) определителя?

· Что такое невязка?

· Сравните достоинства и недостатки точных и приближенных методов.

· Что такое матрица Якоби?

· Надо ли пересчитывать матрицу Якоби на каждом шаге итерации в методе градиента?

· Исходная СЛАУ решается независимо тремя методами – методом Якоби, методом Зейделя и методом градиента. Будут ли равны значения

А) начального приближения (нулевой итерации);

Б) первой итерации?

· При решении СЛАУ (n > 100) итерационными методами решение расходится. Как найти начальное приближение?

Видео:Вычислительные методы алгебры - Метод релаксации, градиентного спуска, минимальных невязокСкачать

Математика для искусственных нейронных сетей для новичков, часть 2 — градиентный спуск

В первой части я забыл упомянуть, что если случайно сгенерированные данные не по душе, то можно взять любой подходящий пример отсюда. Можно почувствовать себя ботаником, виноделом, продавцом. И все это не вставая со стула. В наличии множество наборов данных и одно условие — при публикации указывать откуда взял данные, чтобы другие смогли воспроизвести результаты.

Градиентный спуск

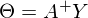
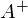
В прошлой части был показан пример вычисления параметров линейной регрессии с помощью метода наименьших квадратов. Параметры были найдены аналитически — , где — псевдообратная матрица. Это решение наглядное, точное и короткое. Но есть проблема, которую можно решить численно. Градиентный спуск — метод численной оптимизации, который может быть использован во многих алгоритмах, где требуется найти экстремум функции — нейронные сети, SVM, k-средних, регрессии. Однако проще его воспринять в чистом виде (и проще модифицировать).

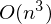
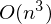
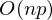
Проблема заключается в том, что вычисление псевдообратной матрицы очень затратно: 2 умножения по , нахождение обратной матрицы — , умножение матрицы вектор , где n — количество элементов в матрице A (количество признаков * количество элементов в тестовой выборке) Если количество элементов в матрице A велико (> 10^6 — например), то даже если в наличии 10000 ядер, нахождение решения аналитически может затянуться. Также первая производная может оказаться нелинейной, что усложнит решение, аналитического решения может не оказаться вовсе или данные могут просто не влезть в память и потребуется итеративный алгоритм. Бывает, что в плюсы записывают и то, что численное решение не идеально точное. В связи с этим функцию стоимости минимизируют численными методами. Задачу нахождения экстремума называют задачей оптимизации. В этой части я остановлюсь на методе оптимизации, который называется градиентный спуск.

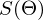
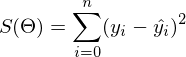
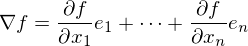
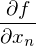
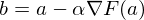
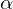
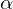
Не будем отходить от линейной регрессии и МНК и обозначим функцию потерь как — она осталась неизменной. Напомню, что градиент — это вектор вида , где — это частная производная. Одним из свойств градиента является то, что он указывает направление, в котором некоторая функция f возрастает больше всего. Доказательство этого следует из определения производной. Пара доказательств. Возьмем некоторую точку a — в окрестности этой точки функция F должна быть определена и дифференцируема, тогда вектор антиградиента будет указывать на направление, в котором функция F убывает быстрее всего. Отсюда делается вывод, что в некоторой точке b, равной , при некотором малом значение функции будет меньше либо равным значению в точке а. Можно представить это, как движение вниз по холму — сделав шаг вниз, текущая позиция будет ниже, чем предыдущая. Таким образом, на каждом следующем шаге высота будет как минимум не увеличиваться. Формальное определение. Исходя из этих определений можно получить формулу для нахождения неизвестных параметров (это просто переписанная версия формулы выше):

— это шаг метода. В задачах машинного обучения его называют скоростью обучения.

Метод очень прост и интуитивен, возьмем простой двумерный пример для демонстрации:

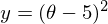
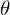
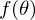
Необходимо минимизировать функцию вида . Минимизировать значит найти при каком значении функция принимает минимальное значение. Определим последовательность действий:

1) Необходима производная по :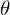
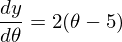
2) Установим начальное значение 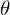= 0
3) Установим размер шага — попробуем несколько значений — 0.1, 0.9, 1.2, чтобы посмотреть как этот выбор повлияет на сходимость.
4) 25 раз подряд выполним указанную выше формулу: 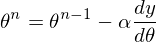Так как неизвестный параметр только один, то и формула только одна.

Код крайне прост. Исключая определение функций, весь алгоритм уместился в 3 строки:

Весь процесс можно визуализировать примерно так (синяя точка — значение на предыдущем шаге, красная — текущее):

Или же для шага другого размера:

При значении, равном 1.2, метод расходится, каждый шаг опускаясь не ниже, а наоборот выше, устремляясь в бесконечность. Шаг в простой реализации подбирается вручную и его размер зависит от данных — на каких-нибудь ненормализованных значениях с большим градиентом и 0.0001 может приводить к расхождению.

Вот еще пример с «плохой» функцией. В первой анимации метод также расходится и будет долго блуждать по холмам из-за слишком высокого шага. Во втором случае был найден локальный минимум и варьируя значение скорости не получится заставить метод найти минимум глобальный. Этот факт является одним недостатков метода — он может найти глобальный минимум только если функция выпуклая и гладкая. Или если повезет с начальными значениями.

Плохая функция:

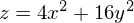
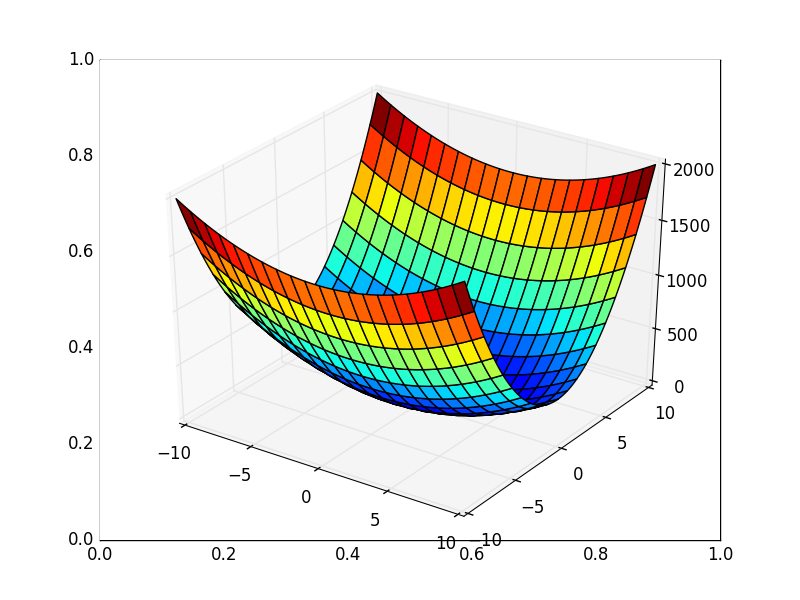
Также возможно рассмотреть работу алгоритма на трехмерном графике. Часто рисуют только изолинии какой-то фигуры. Я взял простой параболоид вращения: . В 3D выглядит он так: , а график с изолиниями — «вид сверху».

Также обратите внимание, что все линии градиента, направлены перпендикулярно изолиниям. Это означает, что двигаясь в сторону антиградиента, не получится за один шаг сразу же прыгнуть в минимум — градиент указывает совсем не туда.

После графического пояснения, найдем формулу для вычисления неизвестных параметров 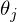линейной регрессии с МНК.

Если бы количество элементов в тестовой выборке было равно единице, то формулу можно было бы так и оставить и считать. В случае, когда в наличии n элементов алгоритм выглядит так:

Повторять v раз
<

для каждого j одновременно.
>, где n — количество элементов в обучающей выборке, v — количество итераций

Требование одновременности означает, что производная должна быть вычислена со старыми значениями theta, не стоит вычислять сначала отдельно первый параметр, затем второй и т.д., потому что после изменения первого параметра отдельно, производная также изменит свое значение. Псевдокод одновременного изменения:

Если вычислять значения параметров по одиночке, то это уже будет не градиентный спуск. Допустим, у нас трехмерная фигура и если вычислять параметры один за одним, то можно представить этот процесс как движение только по одной координате за раз — один шажок по x координате, затем шажок по y координате и т.д. ступеньками, вместо движения в сторону вектора антиградиента.

Приведенный выше вариант алгоритма называют пакетный градиентный спуск. Количество повторений можно заменить на фразу «Повторять, пока не сойдется». Эта фраза означает, что параметры будут корректироваться до тех пор, пока предыдущее и текущее значения функции стоимости не сравняются. Это значит, что локальный или глобальный минимум найден и дальше алгоритм не пойдет. На практике равенства достичь невозможно и вводится предел сходимости . Его устанавливают какой-нибудь малой величиной и критерием остановки является то, что разность предыдущего и текущего значений меньше предела сходимости — это значит, что минимум достигнут с нужной, установленной точностью. Выше точности (меньше ) — больше итераций алгоритма. Выглядит это как-то так:

Так как пост неожиданно растянулся, я бы хотел его на этом завершить — в следующей части я продолжу разбор градиентного спуска для линейной регрессии с МНК.