Московский Государственный Технически Университет
«МАМИ»
Лабораторная работа №3 по курсу «Вычислительная Математика»
«РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ»
3. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
Справочная информация
Численные методы решения систем линейных алгебраических уравнений
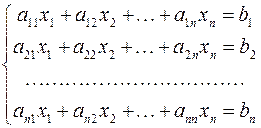
записываемых в матричной форме в виде

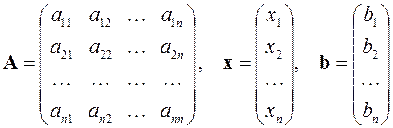
делятся на точные и итерационные. Они используются для систем, у которых количество неизвестных равно количеству уравнений и матрица A — не вырождена (её определитель не равен нулю). Точными методами условно называют методы, которые дают решение задачи посредством конечного числа арифметических операций. Итерационные методы позволяют получить решение системы как предел бесконечной последовательности его приближений. При применении итерационных методов существенным вопросом является вопрос об их сходимости.
Точные методы, к которым относятся метод Гауссаи его разновидности, не имеют дополнительных ограничений на свойства матрицы системы.
В основе метода Гаусса лежит идея последовательного исключения неизвестных, приводящая исходную систему с квадратной матрицей к легко разрешимой системе с верхней треугольной матрицей

Данное преобразование может быть осуществлено многими способами. Однако все они основаны на свойстве систем, которое заключается в неизменности их решений при умножении любого уравнения на отличную от нуля постоянную или его замене на сумму с любым другим уравнением.
Один из простейших способов исключения состоит в следующем. Первое уравнение системы

которое на этом шаге считается ведущим, нормируется – делится на значение диагонального элемента a11

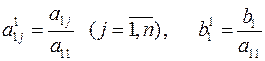
Если в исходной системе a11= 0, то в качестве первого уравнения следует взять любое другое с ненулевым первым коэффициентом, поменяв их местами. Полученное уравнение умножается на первый коэффициент второго уравнения a21 и вычитается из него. В результате во втором уравнении пропадает слагаемое a21x1, содержащее первое неизвестное x1. Такие же операции проводятся со всеми последующими уравнениями. В результате система уравнений принимает вид

Далее процесс повторяется. За ведущее берется второе уравнение и исключается неизвестное x2 из всех уравнений, начиная с третьего

Таким образом, за n шагов система уравнений последовательно сводится к треугольному виду, при этом для последнего уравнения выполняется только операция нормирования:

Полученная система с верхней треугольной матрицей может быть легко разрешена относительно неизвестных. Последнее уравнение системы определяет значение xn, что позволяет определить xn–1 из предпоследнего уравнения как

Выполняя аналогичные подстановки найденных неизвестных в вышестоящие уравнения, удается определить все компоненты решения xn–2. x2, x1.
Метод Гаусса даёт точное решение, если все исходные данные точны и все вычисления производятся точно. На практике, при выполнении вычислений, неизбежно проводятся округления. Ошибка округлений вносит погрешность в решение метода Гаусса. Таким образом, при операциях с округленными десятичными числами метод Гаусса даёт не точное решение xт системы линейных алгебраических уравнений, а некоторое приближённое решение 


Степень отличия приближённого решения от точного определяется длиной разрядной сетки ЭВМ: чем больше разрядов в ней учитывается, тем это отличие меньше.
При определении погрешности вектора решения необходимо учитывать, что его компоненты в общем случае могут иметь разную погрешность. В силу этого погрешность решения принято оценивать по его норме

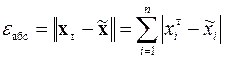

где двойные модульные скобки 
Для определения величины погрешности полученного решения 

а затем посредством повторного решения системы уравнений
находится вектор погрешностей 



так и его относительная погрешность

Величина погрешности решения системы уравнений, получаемого методом Гаусса, зависит от двух основных факторов. Первый из них, как это было сказано выше – длина разрядной сетки, используемой в процессе вычислений, а второй – обусловленность матрицы системы. Обусловленность матрицы можно рассматривать как степень её чувствительности к накоплению ошибок округления в процессе преобразований. Снижение величины погрешности решения может быть достигнуто увеличением длины разрядной сетки. Повлиять на величину погрешности посредством изменения степени обусловленности матрицы системы невозможно, так как она является одной из её характеристик и изменение степени обусловленности матрицы требует изменения самой матрицы.
Метод Гаусса с выбором главного элемента
Основное накопление погрешностей решения в методе Гаусса происходит на этапе приведения системы к треугольному виду. Механизм накопления основной части этой погрешности заключается в привнесении погрешностей вычисления коэффициентов ведущего уравнения в коэффициенты последующих уравнений при исключении каждого очередного неизвестного. Анализ соотношений метода Гаусса показывает, что погрешности вычисления коэффициентов ведущего уравнения привносятся в соответствующие коэффициенты всех последующих уравнений в долях отношений этих коэффициентов к диагональному (главному) коэффициенту ведущего уравнения. В связи с этим привносимая погрешность будет тем меньше, чем меньше доли этих отношений. Поэтому в методе Гаусса с выбором главного элемента на каждом шаге исключения i-го неизвестного в качестве ведущего используетсяуравнение (с i-го по n-ое), содержащее максимальный по модулю коэффициент – главныйэлемент. При этом в качестве него может использоваться один из коэффициентов i-го столбца, i-ой строки или всей непреобразованной части матрицы. Первый подход называется выбором главного элементапостолбцу, второй – по строке, а третий – по всейматрице. При использовании двух последних происходит перестановка столбцов матрицы системы. Это приводит к изменению порядка следования компонент вектора неизвестных и требует его восстановления по окончании процесса решения.
В качестве примера применения метода Гаусса можно рассмотреть задачу отыскания решения следующей системы уравнений
при ограничении разрядной сетки вычислений до трёх знаков и с оценкой погрешности получаемого решения.
Поставленная задача будет решаться методом Гаусса с выбором главного элемента по столбцу.
а. Выбор главного элемента среди элементов первого столбца

б. Нормировка первого уравнения

в. Исключение элементов первого столбца

г. Выбор главного элемента среди элементов второго столбца второго и третьего уравнений
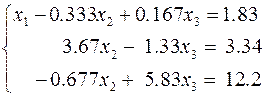
д. Нормировка второго уравнения

е. Исключение элементов второго столбца

ё. Нормировка последнего уравнения

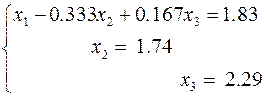

В итоге получено решение системы уравнений

3. Погрешность найденного решения.
а. Пересчёт вектора правых частей системы
б. Формирование системы уравнений, определяющей погрешности решения

в. Решение системы относительно погрешностей оно выполняется аналогично пунктам 1 и 2. Прямой ход (пункт 1) даёт следующую систему с верхней треугольной матрицей

а обратный ход позволяет получить решение

г. Оценка абсолютной и относительной погрешностей решения системы линейных алгебраических уравнений

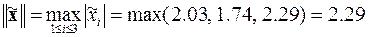

Реализация описанного метода без нахождения погрешности решения в рамках программы Excel приведена на рис.1.
О выборе метода решения систем уравнений
Каждый из рассмотренных методов имеет свои достоинства и недостатки. В частности, метод Гаусса позволяет получить решение за конечное число шагов. Для этого требуется выполнить n(n 2 + 3n – 1)/3 операций умножения и деления и n(n – 1)(2n + 5)/6 операций сложения и вычитания, количество которых при больших порядках системы (n > 100) можно принять равным n 3 /3 в обоих случаях. Однако его методические ошибки, связанные с размером разрядной сетки вычислений, резко нарастают с увеличением порядка системы и не позволяют применять его для систем высоких порядков без использования специальных приёмов.
Итерационные методы позволяют получать решение систем бóльшего порядка. Для выполнения каждой итерации с их помощью необходимо выполнить n(n + 1) операций умножения и деления и столько же операций сложения и вычитания. При больших порядках системы уравнений (n > 100) их количество можно принять равным n 2 . Из сравнения трудоёмкости итерационных методов и метода Гаусса следует оценка, которой можно руководствоваться при окончательном выборе метода решения системы при необходимости его многократного нахождения. Если количество итераций, требуемое для получения решения системы итерационными методами, не превышает n/3, то выгоднее применять их, а не методы типа Гаусса. Однако здесь следует помнить, что итерационные методы требуют, чтобы матрица системы обладала определёнными свойствами, обеспечивающими их сходимость. Необходимо также отметить, что выполнение этих требований часто не гарантирует высокой скорости их сходимости.
- Метод главных элементов.
- Методы решения систем линейных алгебраических уравнений (СЛАУ) с примерами
- Методы решения систем линейных алгебраических уравнений (СЛАУ)
- Метод Крамера
- Матричный способ решения СЛАУ
- Метод Гаусса
- Ранг матрицы. Теорема Кронекера-Капелли
- Следствия из теоремы Кронекера — Капелли
- 🎥 Видео
Видео:6 способов в одном видеоСкачать

Метод главных элементов.
Сумы 2006
Содержание
Постановка задачи
2. Точные методы решения СЛАУ
3. Практическая реализация метода Халецкого
3.1 Программа на языке Pascal
3.2 Решение в Excel
Решить систему линейных алгебраических уравнений, используя точный метод численного решения (схему Халецкого).
Введение
Существует несколько способов решения таких систем, которые в основном делятся на два типа: 1) точные методы, представляющие собой конечные алгоритмы для вычисления корней системы, 2) итерационные методы, позволяющие получать корни системы с заданной точностью путем сходящихся бесконечных процессов.
Для того чтобы система линейных алгебраических уравнений имела решение, необходимо и достаточно, чтобы ранг основной матрицы был равен рангу расширенной матрицы. Если ранг основной матрицы равен рангу расширенной матрицы и равен числу неизвестных, то система имеет единственное решение. Если ранг основной матрицы равен рангу расширенной матрицы, но меньший числа неизвестных, то система имеет бесконечно решений.
Пример системы линейных уравнений:
Или в матричном виде: 
где 


Точные методы решения СЛАУ
Метод главных элементов.
Пусть дана система линейных алгебраических уравнений. Рассмотрим расширенную матрицу, состоящую из коэффициентов системы a[i,j] и свободных членов b[i]. Метод главных элементов — это обобщение метода исключения переменных (метода Гаусса). Обозначим матрицу, состоящую из коэффициентов при неизвестных и столбца свободных членов исходной системы за M.
Выбираем наибольший по модулю элемент, не принадлежащий столбцу свободных членов. Пусть это будет 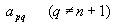
Далее производим следующие преобразования: к каждой неглавной строке прибавим главную строку, умноженную на соответствующий множитель 



последняя, из которых представляет двучленную матрицу — строку, её также будем считать главной строкой. Для определения неизвестных объединяем в систему все главные строки, начиная с последней. После надлежащего изменения нумерации неизвестных получается система с треугольной матрицей, из которой легко шаг за шагом найти неизвестные данной системы.
Заметим, что метод Гаусса является частным случаем, метода главных элементов, а схема метода Гаусса получается, если за главный элемент всегда выбирать левый верхний элемент соответствующей матрицы. Запрограммировать метод главных элементов непросто, поэтому чтобы уменьшить вычислительную погрешность, применяют метод Гаусса с выбором главного элемента. Необходимое условие применения метода главных элементов: определитель системы не равен нулю.
Видео:Математика без Ху!ни. Метод Гаусса.Скачать

Методы решения систем линейных алгебраических уравнений (СЛАУ) с примерами
Содержание:
Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Методы решения систем линейных алгебраических уравнений (СЛАУ)
Метод Крамера
Определение: Системой линейных алгебраических уравнений (СЛАУ) называется выражение
Определение: Определитель, составленный из коэффициентов при неизвестных, называется главным определителем системы
Крамер предложил следующий метод решения СЛАУ: умножим главный определитель на 
Второй столбец умножим на 



Согласно записи СЛАУ первый столбец получившегося определителя представляет собой столбец свободных коэффициентов, т.е.
Определение: Определитель 
Поступая аналогично тому, как описано выше, найдем все вспомогательные определители СЛАУ:
31. Для того чтобы найти вспомогательный определитель i, надо в главном определителе СЛАУ заменить столбец i на столбец свободных коэффициентов.
Определение: Полученные выше соотношения называются формулами Крамера. Используя формулы Крамера, находят неизвестные величины 
- если главный определитель системы отличен от нуля (
), то система имеет единственное решение;
- если главный определитель системы равен нулю (
), а хотя бы один из вспомогательных определителей отличен от нуля (
или
, или, . или
), то система не имеет решений (деление на нуль запрещено);
- если все определители системы равны нулю (
), то система имеет бесчисленное множество решений.
Пример:
Решить СЛАУ методом Крамера
Решение:
Прежде всего, обращаем внимание на то, что в последнем уравнении переменные записаны в неправильном порядке, в этом случае говорят, что СЛАУ записана в ненормализованном виде. Нормализуем СЛАУ, для чего запишем неизвестные в последнем уравнении системы в правильном порядке, чтобы одноименные неизвестные были записаны друг под другом
Найдем главный определитель СЛАУ (раскрываем по первой строке)
Так как главный определитель системы отличен от нуля, то СЛАУ имеет единственное решение. Найдем три вспомогательных определителя
Воспользуемся формулами Крамера
Замечание: После нахождения решения СЛАУ надо обязательно провести проверку, для чего найденные числовые значения неизвестных подставляется в нормализованную систему линейных алгебраических уравнений.
Выполним проверку 
Матричный способ решения СЛАУ
Для решения СЛАУ матричным способом введем в рассмотрение матрицу, составленную из коэффициентов при неизвестных 

Тогда СЛАУ можно записать в матричном виде 





Пример:
Решить СЛАУ матричным способом
Решение:
Введем в рассмотрение следующие матрицы
Найдем матрицу 
Пример:
Решение:
Найдем алгебраические дополнения всех элементов 


Отсюда находим, что х = 1; y = l; z = l.
Метод Гаусса
Метод Гаусса или метод исключения неизвестных состоит в том, чтобы за счет элементарных преобразований привести СЛАУ к треугольному виду. Покажем использование расширенной матрицы, составленной из коэффициентов при неизвестных и расширенной за счет столбца свободных коэффициентов, для приведения СЛАУ к треугольному виду на примере системы, рассматриваемой в этой лекции. Расширенная матрица для СЛАУ имеет вид:
Замечание: В методе Гаусса желательно, чтобы первая строка расширенной матрицы начиналась с единицы.
Обменяем в расширенной матрице первую и вторую строки местами, получим 

Умножим элементы первой строки на (—1) и прибавим к соответствующим элементам третьей строки 

Из первого уравнения находим, что х = 1.
Вывод: Из вышеизложенного материала следует, что вне зависимости от
способа решения СЛАУ всегда должен получаться один и тот же ответ.
Замечание: После нахождения решения СЛАУ надо обязательно выполнить проверку, то есть подставить полученные значения неизвестных в заданную СЛАУ и убедиться в тождественности левой части всех равенств системы соответствующим правым частям. Отметим, что задание СЛАУ всегда верно, то есть, если проверка показывает нарушение оговоренной тождественности, то надо искать ошибку в проведенных вычислениях.
Ранг матрицы. Теорема Кронекера-Капелли
Определение: Рангом матрицы 
Если 
При вычислении ранга необходимо начинать вычислять миноры 2 порядка, затем миноры 3 порядка и так далее, пока не будут найдены миноры, обращающиеся в нуль. Если все миноры порядка p равны нулю, то и все миноры, порядок которых больше p, равны нулю.
Пример:
Найти ранг матрицы
Решение:
Очевидно, что среди миноров второго порядка есть миноры отличные от нуля, например, 


Теорема Кронекера-Капелли (критерий совместности СЛАУ). Для совместности системы линейных алгебраических уравнений (СЛАУ) необходимо и достаточно, чтобы ранг расширенной матрицы совпадал с рангом основной матрицы, составленной из коэффициентов при неизвестных величинах.
Видео:Матричный метод решения систем уравненийСкачать

Следствия из теоремы Кронекера — Капелли
Следствие: Если ранг матрицы совместной системы равен числу неизвестных, то система имеет единственное решение (то есть она определенная).
Следствие: Если ранг матрицы совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений (т.е. она неопределенная).
В случае неопределенной системы решения ищут следующим образом: выбираются главные неизвестные, число которых равно рангу, а остальные неизвестные считаются свободными; далее главные неизвестные выражаются через свободные и получают множество решений, зависящих от свободных неизвестных. Это множество решений называется общим решением системы. Придавая свободным неизвестным различные произвольные значения, получим бесчисленное множество решений, каждое из которых называется частным решением системы.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Скалярное произведение и его свойства
- Векторное и смешанное произведения векторов
- Преобразования декартовой системы координат
- Бесконечно малые и бесконечно большие функции
- Критерий совместности Кронекера-Капелли
- Формулы Крамера
- Матричный метод
- Экстремум функции
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
🎥 Видео
Метод Гаусса Пример РешенияСкачать

Решение системы уравнений методом обратной матрицы - bezbotvyСкачать

Решение системы уравнений методом ГауссаСкачать

Решение системы линейных уравнений методом ГауссаСкачать

метод Гаусса СИСТЕМА ЛИНЕЙНЫХ УРАВНЕНИЙ решение СЛАУСкачать

Метод Гаусса и метод Жордана-Гаусса ➜ 2 метода за 7 минутСкачать

Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать

Система уравнений. Метод алгебраического сложенияСкачать

Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Решение системы линейных уравнений графическим методом. 7 класс.Скачать

12. Решение систем линейных уравнений методом ГауссаСкачать

Система линейных уравнений. Общее решение. Метод ГауссаСкачать

МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать

Решение системы уравнений методом обратной матрицы.Скачать

9. Метод обратной матрицы для решения систем линейных уравнений / матричный методСкачать

Крамера. Гаусса. Матричный метод. Система линейных уравнений. 3 способа решенияСкачать









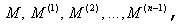







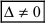 ), то система имеет единственное решение;
), то система имеет единственное решение;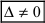 ), а хотя бы один из вспомогательных определителей отличен от нуля (
), а хотя бы один из вспомогательных определителей отличен от нуля ( 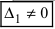 или
или 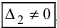 , или, . или
, или, . или 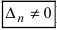 ), то система не имеет решений (деление на нуль запрещено);
), то система не имеет решений (деление на нуль запрещено);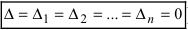 ), то система имеет бесчисленное множество решений.
), то система имеет бесчисленное множество решений.












