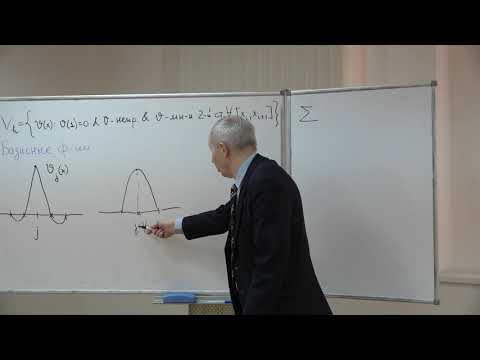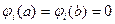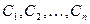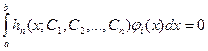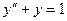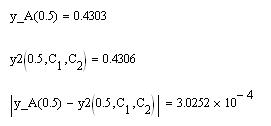Метод галеркина для уравнений в частных производных

Видео:Сеточные методы решения дифференциальных уравнений в частных производных.Скачать

Метод галеркина для решения краевых задач

Метод Галеркина используется для приближенного решения краевых задач для дифференциальных уравнений, как обыкновенных, так и в частных производных.

Рассмотрим краевую задачу

(3.1)

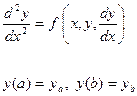
Для ее приближенного решения выберем какую-либо последовательность базисных функций

(3.2)

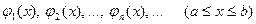
т. е. последовательность функций, удовлетворяющих соответствующим однородным краевым условиям

и обладающих свойством полноты. Последнее означает, что любую функцию из достаточно широкого класса, удовлетворяющую указанным однородным краевым условиям, можно разложить в ряд по функциям (3.2).

Чаще всего полагают

или , .

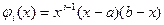
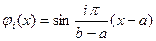
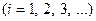
Кроме того, надо выбрать какую-нибудь функцию , удовлетворяющую краевым условиям, указанным в (3.1), например,

или

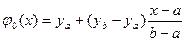
Приближенное решение задачи (3.1) ищется в виде

, (3.3)

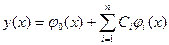
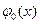
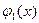
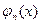
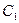
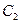
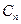
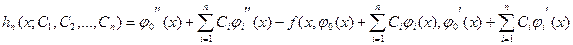
где функции , , … мы задаем, а постоянные , , … , подбираем. Тогда краевые условия, указанные в (3.1), заведомо удовлетворяются, а при подстановке выражения (3.3) в дифференциальное уравнение получается невязка (т. е. разность между левой и правой частями уравнения)

.

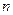
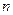
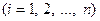
С ее помощью получаем систему из уравнений с неизвестными для определения

.

3.2. Реализация метода Галеркина в|посредством| MathCad

Пример. Найти методом Галеркина приближенное решение краевой задачи

, .

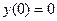
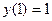
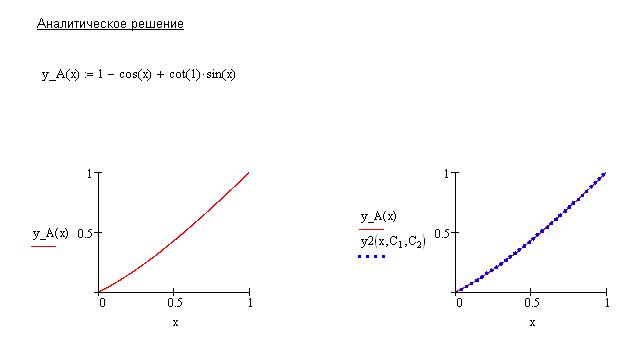
Приведем решение краевой задачи с помощью|посредством| программного комплекса MathCad:

Сравним, значения точного и приближенного решений:

например, при 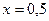имеем

Как видим, погрешность близка к 0,03 %. Для получения более точного решения необходимо использовать большее количество базисных функций.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Увлечёшься девушкой-вырастут хвосты, займёшься учебой-вырастут рога 9966 — | 7768 — или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

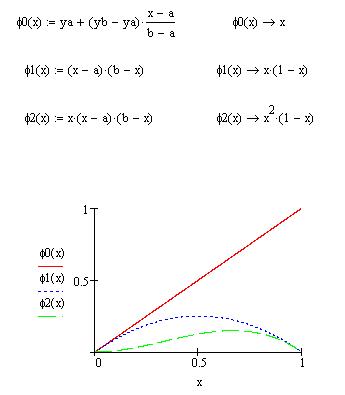
Будем искать приближенное решение этой краевой задачи в виде суммы

Пусть дано дифференциальное уравнение с линейными краевыми условиями

где % Читайте также: Бумага для принтера epson l805

x ), которая на [а, Ь] будет сколь угодно точно приближать функцию у(х) вместе с ее производными У(х) и у»(х).

Докажем, что если для некоторой функции F(x) и полной системы функций

причем с_кк 5*0, иначе (р_к . Здесь оператор L [ ⋅ ] может содержать частные или полные производные искомой функции.

Видео:Метод конечных элементов. Основы 1.1.3 - Метод ГалеркинаСкачать

Содержание

Видео:Уравнения в частных производных первого порядка| poporyadku.schoolСкачать

Основа метода [ править | править код ]

Первым шагом в реализации метода Галёркина является выбор набора базисных функций, которые:

• удовлетворяют граничным условиям.
• в пределе бесконечного количества элементов базиса образуют полную систему.

Конкретный вид функций определяется из специфики задачи и удобства работы. Часто применяются тригонометрические функции, ортогональные полиномы (полиномы Лежандра, Чебышёва, Эрмита и др.).

Решение представляется в виде разложения по базису:

ψ ( x ) = ∑ k = 1 n α k ϕ k ( x ) . alpha _ phi _ (x).>

Затем приближённое решение подставляется в исходное дифференциальное уравнение, и вычисляется его невязка. Для однородного уравнения:

L [ ∑ k = 1 n α k ϕ k ( x ) ] = N ( x ) . alpha _ phi _ (x)
ight]=N(x).>

Для неоднородного уравнения L [ u ] = f ( x ) невязка будет иметь вид N ( x ) = L [ u ] − f ( x ) .

Далее выдвигается требование ортогональности невязки к базисным функциям, то есть:

∫ a b N ( x ) ϕ k ( x ) ρ ( x ) d x = 0. (x)
ho (x)dx>=0.>

Отсюда получается однородная система уравнений для коэффициентов в разложении, и удаётся приближённо найти собственные значения задачи.

Видео:Приведение ДУ 2 порядка в частных производных к каноническому видуСкачать

Пример [ править | править код ]

ψ ″ + λ ψ = 0 ,

с граничными условиями:

ψ ( 0 ) = ψ ( 1 ) = 0.

Решение данного уравнения известно:

ψ ( x ) = sin ⁡ π n x , λ = π 2 n 2 , n = 1 , 2.. n^ ,qquad n=1,2..>

Для первого нетривиального решения ( n = 1 ) собственное число равно λ = π 2 ≈ 9 , 869. approx 9,869. > .

Теперь применим метод Галёркина. Выберем сперва одну базисную функцию:

ϕ 0 ( x ) = x ( 1 − x ) , ψ ( x ) = a 0 ϕ 0 ( x ) . (x)=x(1-x),qquad psi (x)=a_ phi _ (x).>

Подставляя в уравнение, получим невязку:

N ( x ) = a ( ϕ ″ + λ ϕ ) ,

и требование ортогональности невязки перепишется в виде:

∫ 0 1 ϕ ″ ϕ d x + λ ∫ 0 1 ϕ 2 d x = 0. ^

+lambda int limits _ ^

dx>=0.>

λ = − ∫ 0 1 ϕ ″ ϕ d x ∫ 0 1 ϕ 2 d x = ∫ 0 1 ( ϕ ′ ) 2 d x ∫ 0 1 ϕ 2 d x . ^

over int limits _ ^

dx>>= ^ dx> over int limits _ ^

dx>>.>

В приводимом здесь примере получается λ = 10 , что менее чем на 1,5 % отличается от точного решения. Задание большего числа базисных функций позволяет уточнить уже известное значение λ, а также получить первое приближение для следующего (соответствующего n=2).

Представим решение в виде линейной комбинации n функций:

ψ ( x ) = ∑ k = 1 n α k ϕ k ( x ) . alpha _ phi _ (x).>

N = ∑ k = 1 n N k ( x ) N_ (x)> .

Система уравнений для коэффициентов разложения:

∑ k = 1 n α k ∫ a b ϕ j N k d x = 0 , j = 1.. n . alpha _ int limits _^

N_ dx>=0,quad j=1..n.>

В этом случае собственные значения находятся из условия разрешимости системы (равенство нулю её определителя):

det ⁡ ( A j k ) = 0 , A j k = ∫ a b ϕ j N k d x left(A_
ight)=0,quad A_ =int limits _^

N_ dx>>

Важно помнить, что сходимость метода Галёркина не всегда быстро достигается. Успешное применение возможно только для т. н. самосопряжённых задач, то есть инвариантных к эрмитовому сопряжению.

Видео:Математика без Ху!ни. Частные производные функции нескольких переменных. Градиент.Скачать

Разновидности [ править | править код ]

Метод Галёркина имеет несколько усовершенствованных вариантов:

• Метод Галёркина — Петрова — разложение решения производится по одному базису, а ортогональность невязки требуется к другому.
• Метод Галёркина — Канторовича — позволяет свести уравнения в частных производных к обыкновенным дифференциальным уравнениям. Например, в двумерной задаче решение представляется в виде: ψ ( x , y ) = ∑ n b n X n ( x ) Y n ( y ) , b_ X_ (x)Y_ (y),>и процедура Галёркина проводится применительно лишь к одним функциям (здесь X n ( x ) (x)>либо Y n ( y ) (y)>). В итоге получается система ОДУ, для решения которых существуют эффективные численные методы. Данный приём подобен известному в квантовой механике методу Хартри — Фока.

Видео:Производная: секретные методы решения. Готовимся к ЕГЭ | Математика TutorOnlineСкачать

Применение [ править | править код ]

Методы Галёркина давно применяются как для решения дифференциальных уравнений с частными производными, так и для формирования основы метода конечных элементов.

Применение метода к исследованию задач устойчивости гидродинамических течений было реализовано Г. И. Петровым, который доказал сходимость метода Галёркина для отыскания собственных значений широкого класса уравнений, включая уравнения для неконсервативных систем, такие, как например уравнения колебаний в вязкой жидкости.

В гидродинамике наиболее эффективно метод Галёркина работает в задачах о конвекции, в силу их самосопряжённости. Задачи о течениях таковыми не являются, и сходимость метода при неудачном выборе базиса может быть сильно затруднена.

Видео:2. Приведение уравнений второго порядка к каноническому видуСкачать

Происхождение названия [ править | править код ]

Метод приобрёл популярность после исследований Бориса Галёркина (1915). Однако этот метод разработал не он, а Вальтер Ритц (1908), на которого Галёркин ссылается в своих первых публикациях. Его также применял Иван Бубнов (1913) для решения задач теории упругости. Поэтому иногда этот метод называют методом Бубнова — Галёркина. Теоретически метод был обоснован советским математиком Мстиславом Келдышем в 1942.

🌟 Видео

Методы приближенного решения дифференциальных уравнений в частных производныхСкачать

Уравнение колебаний струны. Метод разделения переменных. Метод ФурьеСкачать

Разрывный метод ГалёркинаСкачать

Методы решения нелинейных краевых задач для ОДУСкачать

6. Линейные однородные уравнения в частных производных первого порядкаСкачать

6-2. Метод сетокСкачать

Кобельков Г. М. - Численные методы. Часть 2 - Метод Галёркина для полинома второй степениСкачать

Горицкий А. Ю. - Уравнения математической физики - Уравнения с частными производными 1-го порядкаСкачать

АЛГЕБРА С НУЛЯ — Что такое Производная?Скачать

Дифференциальные уравнения не разрешенные относительно производной | poporyadku.schoolСкачать

19. Метод вариации произвольных постоянных. Линейные неоднородные диф уравнения 2-го порядкаСкачать