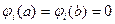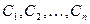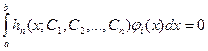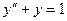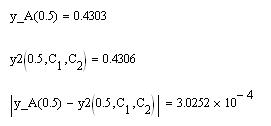Метод галеркина для решения обыкновенных дифференциальных уравнений

Метод Галеркина используется для приближенного решения краевых задач для дифференциальных уравнений, как обыкновенных, так и в частных производных.

Рассмотрим краевую задачу

(3.1)

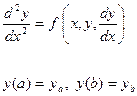
Для ее приближенного решения выберем какую-либо последовательность базисных функций

(3.2)

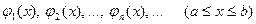
т. е. последовательность функций, удовлетворяющих соответствующим однородным краевым условиям

и обладающих свойством полноты. Последнее означает, что любую функцию из достаточно широкого класса, удовлетворяющую указанным однородным краевым условиям, можно разложить в ряд по функциям (3.2).

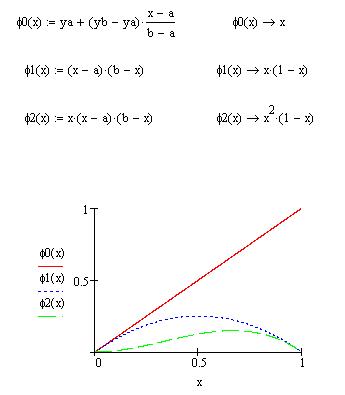
Чаще всего полагают

или , .

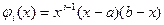
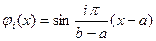
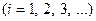
Кроме того, надо выбрать какую-нибудь функцию , удовлетворяющую краевым условиям, указанным в (3.1), например,

или

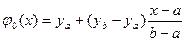
Приближенное решение задачи (3.1) ищется в виде

, (3.3)

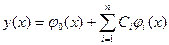
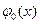
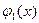
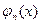
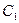
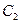
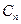
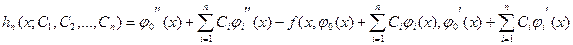
где функции , , … мы задаем, а постоянные , , … , подбираем. Тогда краевые условия, указанные в (3.1), заведомо удовлетворяются, а при подстановке выражения (3.3) в дифференциальное уравнение получается невязка (т. е. разность между левой и правой частями уравнения)

.

С ее помощью получаем систему из уравнений с неизвестными для определения

.

3.2. Реализация метода Галеркина в|посредством| MathCad

Пример. Найти методом Галеркина приближенное решение краевой задачи

, .

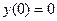
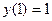
Приведем решение краевой задачи с помощью|посредством| программного комплекса MathCad:

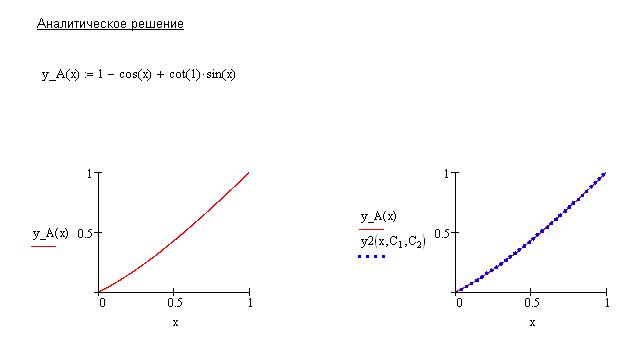
Сравним, значения точного и приближенного решений:

например, при 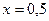имеем

Как видим, погрешность близка к 0,03 %. Для получения более точного решения необходимо использовать большее количество базисных функций.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Увлечёшься девушкой-вырастут хвосты, займёшься учебой-вырастут рога 9966 — | 7768 — или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Будем искать приближенное решение этой краевой задачи в виде суммы

Пусть дано дифференциальное уравнение с линейными краевыми условиями

где % Читайте также: Как давно зарегистрирован вконтакте

x ), которая на [а, Ь] будет сколь угодно точно приближать функцию у(х) вместе с ее производными У(х) и у»(х).

Докажем, что если для некоторой функции F(x) и полной системы функций

причем с_кк 5*0, иначе (р_к . Здесь оператор L [ ⋅ ] может содержать частные или полные производные искомой функции.

Видео:Метод ЭйлераСкачать

Содержание

Видео:7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать

Основа метода [ править | править код ]

Первым шагом в реализации метода Галёркина является выбор набора базисных функций, которые:

• удовлетворяют граничным условиям.
• в пределе бесконечного количества элементов базиса образуют полную систему.

Конкретный вид функций определяется из специфики задачи и удобства работы. Часто применяются тригонометрические функции, ортогональные полиномы (полиномы Лежандра, Чебышёва, Эрмита и др.).

Решение представляется в виде разложения по базису:

ψ ( x ) = ∑ k = 1 n α k ϕ k ( x ) . alpha _ phi _ (x).>

Затем приближённое решение подставляется в исходное дифференциальное уравнение, и вычисляется его невязка. Для однородного уравнения:

L [ ∑ k = 1 n α k ϕ k ( x ) ] = N ( x ) . alpha _ phi _ (x)
ight]=N(x).>

Для неоднородного уравнения L [ u ] = f ( x ) невязка будет иметь вид N ( x ) = L [ u ] − f ( x ) .

Далее выдвигается требование ортогональности невязки к базисным функциям, то есть:

∫ a b N ( x ) ϕ k ( x ) ρ ( x ) d x = 0. (x)
ho (x)dx>=0.>

Отсюда получается однородная система уравнений для коэффициентов в разложении, и удаётся приближённо найти собственные значения задачи.

Видео:Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Пример [ править | править код ]

ψ ″ + λ ψ = 0 ,

с граничными условиями:

ψ ( 0 ) = ψ ( 1 ) = 0.

Решение данного уравнения известно:

ψ ( x ) = sin ⁡ π n x , λ = π 2 n 2 , n = 1 , 2.. n^ ,qquad n=1,2..>

Для первого нетривиального решения ( n = 1 ) собственное число равно λ = π 2 ≈ 9 , 869. approx 9,869. > .

Теперь применим метод Галёркина. Выберем сперва одну базисную функцию:

ϕ 0 ( x ) = x ( 1 − x ) , ψ ( x ) = a 0 ϕ 0 ( x ) . (x)=x(1-x),qquad psi (x)=a_ phi _ (x).>

Подставляя в уравнение, получим невязку:

N ( x ) = a ( ϕ ″ + λ ϕ ) ,

и требование ортогональности невязки перепишется в виде:

∫ 0 1 ϕ ″ ϕ d x + λ ∫ 0 1 ϕ 2 d x = 0. ^

+lambda int limits _ ^

dx>=0.>

λ = − ∫ 0 1 ϕ ″ ϕ d x ∫ 0 1 ϕ 2 d x = ∫ 0 1 ( ϕ ′ ) 2 d x ∫ 0 1 ϕ 2 d x . ^

over int limits _ ^

dx>>= ^ dx> over int limits _ ^

dx>>.>

В приводимом здесь примере получается λ = 10 , что менее чем на 1,5 % отличается от точного решения. Задание большего числа базисных функций позволяет уточнить уже известное значение λ, а также получить первое приближение для следующего (соответствующего n=2).

Представим решение в виде линейной комбинации n функций:

ψ ( x ) = ∑ k = 1 n α k ϕ k ( x ) . alpha _ phi _ (x).>

N = ∑ k = 1 n N k ( x ) N_ (x)> .

Система уравнений для коэффициентов разложения:

∑ k = 1 n α k ∫ a b ϕ j N k d x = 0 , j = 1.. n . alpha _ int limits _^

N_ dx>=0,quad j=1..n.>

В этом случае собственные значения находятся из условия разрешимости системы (равенство нулю её определителя):

det ⁡ ( A j k ) = 0 , A j k = ∫ a b ϕ j N k d x left(A_
ight)=0,quad A_ =int limits _^

N_ dx>>

Важно помнить, что сходимость метода Галёркина не всегда быстро достигается. Успешное применение возможно только для т. н. самосопряжённых задач, то есть инвариантных к эрмитовому сопряжению.

Видео:Методы решения нелинейных краевых задач для ОДУСкачать

Разновидности [ править | править код ]

Метод Галёркина имеет несколько усовершенствованных вариантов:

• Метод Галёркина — Петрова — разложение решения производится по одному базису, а ортогональность невязки требуется к другому.
• Метод Галёркина — Канторовича — позволяет свести уравнения в частных производных к обыкновенным дифференциальным уравнениям. Например, в двумерной задаче решение представляется в виде: ψ ( x , y ) = ∑ n b n X n ( x ) Y n ( y ) , b_ X_ (x)Y_ (y),>и процедура Галёркина проводится применительно лишь к одним функциям (здесь X n ( x ) (x)>либо Y n ( y ) (y)>). В итоге получается система ОДУ, для решения которых существуют эффективные численные методы. Данный приём подобен известному в квантовой механике методу Хартри — Фока.

Видео:Численное решение задачи Коши методом ЭйлераСкачать

Применение [ править | править код ]

Методы Галёркина давно применяются как для решения дифференциальных уравнений с частными производными, так и для формирования основы метода конечных элементов.

Применение метода к исследованию задач устойчивости гидродинамических течений было реализовано Г. И. Петровым, который доказал сходимость метода Галёркина для отыскания собственных значений широкого класса уравнений, включая уравнения для неконсервативных систем, такие, как например уравнения колебаний в вязкой жидкости.

В гидродинамике наиболее эффективно метод Галёркина работает в задачах о конвекции, в силу их самосопряжённости. Задачи о течениях таковыми не являются, и сходимость метода при неудачном выборе базиса может быть сильно затруднена.

Видео:Метод конечных элементов. Основы 1.1.3 - Метод ГалеркинаСкачать

Происхождение названия [ править | править код ]

Метод приобрёл популярность после исследований Бориса Галёркина (1915). Однако этот метод разработал не он, а Вальтер Ритц (1908), на которого Галёркин ссылается в своих первых публикациях. Его также применял Иван Бубнов (1913) для решения задач теории упругости. Поэтому иногда этот метод называют методом Бубнова — Галёркина. Теоретически метод был обоснован советским математиком Мстиславом Келдышем в 1942.

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

ИДЕЯ МЕТОДА ГАЛЁРКИНА Текст научной статьи по специальности « Математика»

Видео:Дифференциальные уравнения. Задача Коши. Метод Эйлера.Скачать

Аннотация научной статьи по математике, автор научной работы — Давронов Жавлон Рустам Угли

В этой статье показано применение метода Галёркина для численного решения краевой задачи, поставленной дифференциальному уравнению . Суть метода показана на примере. Численное решение дифференциальных уравнений на сегодня вызывает большой интерес. Не каждое дифференциальное уравнение имеет аналитическое решение, так как дифференциальные уравнения выражают конкретный, естественный процесс, их приближённое решение приближенно отображает изучаемый процесс. Это показывает прикладной характер изучаемой задачи.

Видео:9. Метод вариации произвольной постоянной ( метод Лагранжа ). Линейные дифференциальные уравнения.Скачать

Похожие темы научных работ по математике , автор научной работы — Давронов Жавлон Рустам Угли

Видео:13. Как решить дифференциальное уравнение первого порядка?Скачать

THE IDEA OF THE GALERKIN METHOD

This article shows the application of the Galerkin method for the numerical solution of the boundary value problem posed to the differential equation. The essence of the method is shown with an example. The numerical solution of differential equations is of great interest today. Not every differential equation has an analytical solution, since differential equations express a specific, natural process, their approximate solution approximately reflects the process under study. This shows the applied nature of the problem under study.

Видео:Математика без Ху!ни. Линейное неоднородное уравнение 1 порядка. Метод вариации постоянной.Скачать

Текст научной работы на тему «ИДЕЯ МЕТОДА ГАЛЁРКИНА»

ИДЕЯ МЕТОДА ГАЛЁРКИНА Давронов Ж.Р. Email: Davronov697@scientifictext.ru

Давронов Жавлон Рустам угли — преподаватель кафедра дифференциальных уравнений, физико-математический факультет, Бухарский государственный университет, г. Бухара, Республика Узбекистан

Аннотaция: в этой статье показано применение метода Галёркина для численного решения краевой задачи, поставленной дифференциальному уравнению. Суть метода показана на примере. Численное решение дифференциальных уравнений на сегодня вызывает большой интерес. Не каждое дифференциальное уравнение имеет аналитическое решение, так как дифференциальные уравнения выражают конкретный, естественный процесс, их приближённое решение приближенно отображает изучаемый процесс. Это показывает прикладной характер изучаемой задачи.

Ключевые слова: дифференциальные уравнения, краевые условия, численное решение, метод Галёркина, погрешность.

THE IDEA OF THE GALERKIN METHOD Davronov J.R.

Davronov Javlon Rustam ugli — Teacher, DEPARTMENT OF DIFFERENTIAL EQUATION, FACULTY OF PHYSICS AND MATHEMATICS, BUKHARA STATE UNIVERSITY, BUKHARA, REPUBLIC OF UZBEKISTAN

Abstract: this article shows the application of the Galerkin methodfor the numerical solution of the boundary value problem posed to the differential equation. The essence of the method is shown with an example. The numerical solution of differential equations is of great interest today. Not every differential equation has an analytical solution, since differential equations express a specific, natural process, their approximate solution approximately reflects the process under study. This shows the applied nature of the problem under study.

Keywords: differential equations, boundary conditions, numerical solution, Galerkin method, error.

Пусть задано уравнение

где L [у] = у» + р (х) у’ + q (х) у, и краевые условия:

Га М = а0у(а) + аху’Са) = А (2.1) Гь М = /?„ У (Ь) + fty’ (Ь) = В; (2.2) |ао| + К1*0 |/?„l + l/?il*0; (2.3) Выберем конечную систему базовых функций ( i = 0 , 1 , • • -,п) , состоящую из части полной системы, и функцию //0 (х) , которая удовлетворяет неоднородные краевые условия

Г[Ц0] = А , Г[У0] = В и функции удовлетворяют однородные краевые условия

Г[1/г]0, Г[[/г] = 0 (i = 1,2,••• ,п) Ищем решение краевой задачи ( 1 ) — (2 . 3 ) — следующим образом

y(x) = U0(x)+YjCiUi(x) (3)

В выбранных нами базовых функциях / (х) , функция y определяется формулой (3), видно, что она удовлетворяет граничным условиям (2.1) — (2.3) при произвольном

выборе коэффициентов С¿. (3) — выражение подставляем в уравнение (1). Это дает следующую ошибку.

R (х, C1,C2,-,Cn) = L[U0]+YjCiL [Ut] — f<x)

Согласно методу Галёркина, мы требуем, чтобы ошибка R была ортогональна базисным функциям U(х) ( ¿ = 1 , 2 ,• • -,п) , достаточно большое количество таких функций обеспечивает умеренно малую погрешность. Насколько близко такое приблизительное решение к конкретному — одна из задач, которая в целом остается открытой. Таким образом, чтобы найти коэффициенты Сг ( i = 1,2, • ■ -,п) приходим к линейной системе уравнений

U1(x)R(x,C1,C2, . Cn)dx = О

I U2(x)R(x,C1,C2. Cn)dx = J a

Un(x)R(x, Cu C2. Cn)dx =

У» + У = _х у( 0) = 0 у( 1) = 0

Решение: На основе метода Галёркина выбираем приближенное решение в следующем виде

где, если берём и ‘ (х) = х’ ( 1 — х) , которые удовлетворяют граничным условиям. Для простоты расчета рассмотрим случай п = 2,

у2(х) = ад(х) + С2 и2 (х) у2(х) = Сх( 1 — х) + С2х2 (1 — х) у2′(х) = Сх( 1 — 2х) + С2(2х — Зх2) У2″00 = -2СХ + 2С2 — 6С2х теперь подставим эти равенства в уравнения.

Уп = У2″00 + У200 = -2СХ + 2С2 + х(Сх — 6С2) + х2(С2 — С) — х3С2 и .

Теперь вычислим следующие интегралы, чтобы найти коэффициенты Сх va С2 :

I Уп^л (x)dx = I f(x)U1(x)dx Jo Jo

I ynU2(x)dx = I f(x)U2(x)dx Jo Jo

после использования первой из этих систем, получим следующее равенство

[ (-2Сх + 2С2 + х(Сх — 6С2) + х2(С2 — С) — х3С2)(х — х2)с?х = [ -х(х — х2)с?х -‘о -‘о

Вычисляя интеграл, получим

Теперь мы упростим второе уравнение системы, сделав то же самое, из чего следует следующее: 6 3 Ci + 5 2 C2 = 2 1 .

Решаем полученную систему линейных уравнений относительно Cx и C2:

Получим, Cx = — и C2 = — e коэффициенты подставляем в приближенное решение

Уп (х) = ( 1 — х) + ¿х2 ( 1 — х) .

Точное решение у (х) = ■—-— х. Погрешность в этом случае е Надоели баннеры? Вы всегда можете отключить рекламу.

📸 Видео

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Практика 1 ИзоклиныСкачать

Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами 4y''-y=x^3-24x #1Скачать

Дифференциальное уравнение. Формула ЭйлераСкачать

2. Дифференциальные уравнения с разделяющимися переменными. Часть 1.Скачать

14. Дифференциальные уравнения второго порядка, допускающие понижение порядкаСкачать