Метод эйлера для решения дифференциальных уравнений явный и неявный

Nickolay.info. Обучение. Лекции по численным методам. Численное решение обыкновенных дифференциальных уравнений

5. Численное решение обыкновенных дифференциальных уравнений

Многие задачи науки и техники сводятся к решению обыкновенных дифференциальных уравнений (ОДУ). ОДУ называются такие уравнения, которые содержат одну или несколько производных от искомой функции. В общем виде ОДУ можно записать следующим образом:

, где x – независимая переменная, — i-ая производная от искомой функции. n — порядок уравнения. Общее решение ОДУ n–го порядка содержит n произвольных постоянных , т.е. общее решение имеет вид .

Для выделения единственного решения необходимо задать n дополнительных условий. В зависимости от способа задания дополнительных условий существуют два различных типа задач: задача Коши и краевая задача. Если дополнительные условия задаются в одной точке, то такая задача называется задачей Коши. Дополнительные условия в задаче Коши называются начальными условиями. Если же дополнительные условия задаются в более чем одной точке, т.е. при различных значениях независимой переменной, то такая задача называется краевой. Сами дополнительные условия называются краевыми или граничными.

Ясно, что при n=1 можно говорить только о задачи Коши.

Примеры постановки задачи Коши:

Примеры краевых задач:

Решить такие задачи аналитически удается лишь для некоторых специальных типов уравнений.

Численные методы решения задачи Коши для ОДУ первого порядка

Постановка задачи. Найти решение ОДУ первого порядка

на отрезке при условии

При нахождении приближенного решения будем считать, что вычисления проводятся с расчетным шагом , расчетными узлами служат точки промежутка [x₀, x_n].

Целью является построение таблицы

т.е. ищутся приближенные значения y в узлах сетки.

Интегрируя уравнение на отрезке , получим

Вполне естественным (но не единственным) путем получения численного решения является замена в нем интеграла какой–либо квадратурной формулой численного интегрирования. Если воспользоваться простейшей формулой левых прямоугольников первого порядка

,

то получим явную формулу Эйлера:

, .

Зная , находим , затем т.д.

Геометрическая интерпретация метода Эйлера:

Пользуясь тем, что в точке x₀ известно решение y(x₀) = y₀ и значение его производной , можно записать уравнение касательной к графику искомой функции в точке : . При достаточно малом шаге h ордината этой касательной, полученная подстановкой в правую часть значения , должна мало отличаться от ординаты y(x₁) решения y(x) задачи Коши. Следовательно, точка пересечения касательной с прямой x = x₁ может быть приближенно принята за новую начальную точку. Через эту точку снова проведем прямую , которая приближенно отражает поведение касательной к в точке . Подставляя сюда (т.е. пересечение с прямой x = x₂), получим приближенное значение y(x) в точке x₂: и т.д. В итоге для i–й точки получим формулу Эйлера.

Явный метод Эйлера имеет первый порядок точности или аппроксимации.

Если использовать формулу правых прямоугольников: , то придем к методу

, .

Этот метод называют неявным методом Эйлера, поскольку для вычисления неизвестного значения по известному значению требуется решать уравнение, в общем случае нелинейное.

Неявный метод Эйлера имеет первый порядок точности или аппроксимации.

Модифицированный метод Эйлера: в данном методе вычисление состоит из двух этапов:

Данная схема называется еще методом предиктор – корректор (предсказывающее – исправляющее). На первом этапе приближенное значение предсказывается с невысокой точностью (h), а на втором этапе это предсказание исправляется, так что результирующее значение имеет второй порядок точности.

Методы Рунге – Кутта: идея построения явных методов Рунге–Кутты p–го порядка заключается в получении приближений к значениям y(x_i+1) по формуле вида

,

.

Здесь a_n, b_nj, p_n, – некоторые фиксированные числа (параметры).

При построения методов Рунге–Кутты параметры функции (a_n, b_nj, p_n) подбирают таким образом, чтобы получить нужный порядок аппроксимации.

Схема Рунге – Кутта четвертого порядка точности:

Пример. Решить задачу Коши:

.

Рассмотреть три метода: явный метод Эйлера, модифицированный метод Эйлера, метод Рунге – Кутта.

Точное решение:

Расчетные формулы по явному методу Эйлера для данного примера:

Расчетные формулы модифицированного метода Эйлера:

Видео:Метод ЭйлераСкачать

Задачи с начальными условиями для систем обыкновенных дифференциальных уравнений

Рассмотрим задачу Коши для системы обыкновенных дифференциальных уравнений $$ begin tag frac &= f_i (t, u_1, u_2, ldots, u_n), quad t > 0\ tag u_i(0) &= u_i^0, quad i = 1, 2, ldots, m. end $$

Используя векторные обозначения, задачу (1), (2) можно записать как задачу Коши $$ begin tag frac<d pmb> &= pmb(t, pmb), quad t > 0, \ tag pmb(0) &= pmb_0 end $$ В задаче Коши необходимо по известному решению в точке ( t = 0 ) необходимо найти из уравнения (3) решение при других ( t ).

Видео:МЗЭ 2022 Численное решение дифференциальных уравнений. Неявный метод Эйлера. Ложкин С.А.Скачать

Численные методы решения задачи Коши

Существует большое количество методов численного решения задачи (3), (4). Вначале рассмотрим простейший явный метод Эйлера и его программную реализацию. Затем будут представлены методы Рунге—Кутта и многошаговые методы.

При построении численных алгоритмов будем считать, что решение этой дифференциальной задачи существует, оно единственно и обладает необходимыми свойствами гладкости.

Идея численных методов решения задачи (3), (4) состоит из четырех частей:

1. Вводится расчетная сетка по переменной ( t ) (время) из ( N_t + 1 ) точки ( t_0 ), ( t_1 ), ( ldots ), ( t_ ). Нужно найти значения неизвестной функции ( pmb ) в узлах сетки ( t_n ). Обозначим через ( pmb^n ) приближенное значение ( pmb(t_n) ).

2. Предполагаем, что дифференциальное уравнение выполнено в узлах сетки.

3. Аппроксимируем производные конечными разностями.

4. Формулируем алгоритм, который вычисляет новые значения ( pmb^ ) на основе предыдущих вычисленных значений ( pmb^k ), ( k 0 ) при ( tauto 0 ).

Видео:Численное решение задачи Коши методом ЭйлераСкачать

Явный метод Эйлера

Проиллюстрируем указанные шаги. Для начала введем расчетную сетку. Очень часто сетка является равномерной, т.е. имеет одинаковое расстояние между узлами ( t_n ) и ( t_ ): $$ omega_tau = . $$

Затем, предполагаем, что уравнение выполнено в узлах сетки, т.е.: $$ pmb^prime (t_n) = pmb(t_n, u(t_n)), quad t_n in omega_tau. $$

Заменяем производные конечными разностями. С этой целью, нам нужно знать конкретные формулы, как производные могут быть аппроксимированы конечными разностями. Простейший подход заключается в использовании определения производной: $$ pmb^prime(t) = lim_ frac<pmb(t+tau) — pmb(t)>. $$

В произвольном узле сетки ( t_n ) это определение можно переписать в виде: $$ begin pmb^prime(t_n) = lim_ frac<pmb(t_n+tau) — pmb(t_n)>. end $$ Вместо того, чтобы устремлять шаг сетки к нулю, мы можем использовать малый шаг ( tau ), который даст численное приближение ( u^prime(t_n) ): $$ begin pmb^prime(t_n) approx frac<pmb^ — pmb^>. end $$ Такая аппроксимация известна как разностная производная вперед и имеет первый порядок по ( tau ), т.е. ( O(tau) ). Теперь можно использовать аппроксимацию производной. Таким образом получим явный метод Эйлера: $$ begin tag frac<pmb^ — pmb^n> = pmb(t_n, pmb^). end $$

Четвертый шаг заключается в получении численного алгоритма. Из (5) следует, что мы должны знать значение ( y^n ) для того, чтобы решить уравнение (5) относительно ( y^ ) и получить формулу для нахождения приближенного значения искомой функции на следующем временном слое ( t_ ): $$ begin tag pmb^ = pmb^n + tau pmb(t_n, pmb^) end $$

При условии, что у нас известно начальное значение ( pmb^0 = pmb_0 ), мы можем использовать (6) для нахождения решений на последующих временных слоях.

Программная реализация явного метода Эйлера

Выражение (6) может быть как скалярным так и векторным уравнением. И в скалярном и в векторном случае на языке Python его можно реализовать следующим образом

При решении системы (векторный случай), u[n] — одномерный массив numpy длины ( m+1 ) (( m ) — размерность задачи), а функция F должна возвращать numpy -массив размерности ( m+1 ), t[n] — значение в момент времени ( t_n ).

Таким образом численное решение на отрезке ( [0, T] ) должно быть представлено двумерным массивом, инициализируемым нулями u = np.zeros((N_t+1, m+1)) . Первый индекс соответствует временному слою, а второй компоненте вектора решения на соответствующем временном слое. Использование только одного индекса, u[n] или, что то же самое, u[n, :] , соответствует всем компонентам вектора решения.

Функция euler решения системы уравнений реализована в файле euler.py:

Строка F_ = lambda . требует пояснений. Для пользователя, решающего систему ОДУ, удобно задавать функцию правой части в виде списка компонент. Можно, конечно, требовать чтобы пользователь возвращал из функции массив numpy , но очень легко осуществлять преобразование в самой функции решателе. Чтобы быть уверенным, что результат F будет нужным массивом, который можно использовать в векторных вычислениях, мы вводим новую функцию F_ , которая вызывает пользовательскую функцию F «прогоняет» результат через функцию assaray модуля numpy .

Видео:Метод Эйлера. Решение систем ДУСкачать

Неявный метод Эйлера

При построении неявного метода Эйлера значение функции ( F ) берется на новом временном слое, т.е. для решении задачи (5) используется следующий метод: $$ begin tag frac<pmb^ — pmb^n> = pmb(t_, pmb^). end $$

Таким образом для нахождения приближенного значения искомой функции на новом временном слое ( t_ ) нужно решить нелинейное уравнение относительно ( pmb^ ): $$ begin tag pmb^ — tau pmb(t_, pmb^) — y^n = 0. end $$

Для решения уравнения (8) можно использовать, например, метод Ньютона.

Программная реализация неявного метода Эйлера

Функция backward_euler решения системы уравнений реализована в файле euler.py:

Отметим, что для нахождения значения u[n+1] используется функция fsolve модуля optimize библиотеки scipy . В качестве начального приближения для решения нелинейного уравнения используется значение искомой функции с предыдущего слоя u[n] .

Видео:МЗЭ 2022 Пример решения явным и неявным методом ЭйлераСкачать

Методы Рунге—Кутта

Одношаговый метод Рунге—Кутта в общем виде записывается следующим образом: $$ begin tag frac<pmb^ — pmb^n> = sum_^s b_i pmb_i, end $$ где $$ begin tag pmb_i = pmbleft( t_n + c_itau, pmb^n + tau sum_^s a_pmb_j right), quad i = 1, 2, ldots, s. end $$ Формула (9) основана на ( s ) вычислениях функции ( pmb ) и называется ( s )-стадийной. Если ( a_ = 0 ) при ( j geq i ) имеем явный метод Рунге—Кутта. Если ( a_ = 0 ) при ( j > i ) и ( a_ ne 0 ), то ( pmb_i ) определяется неявно из уравнения $$ begin tag pmb_i = pmbleft( t_n + c_itau, pmb^n + tau sum_^ a_pmb_j + tau a_ pmb_i right), quad i = 1, 2, ldots, s. end $$ О таком методе Рунге—Кутта говорят как о диагонально-неявном.

Одним из наиболее распространенных является явный метод Рунге-Кутта четвертого порядка: $$ begin tag pmb_1 & = pmb(t_n, pmb^n), &quad pmb_2 &= pmbleft( t_n + frac, pmb^n + tau frac<pmb_1> right),\ pmb_3 &= pmbleft( t_n + frac, pmb^n + tau frac<pmb_2> right), &quad pmb_4 &= pmbleft( t_n + tau, pmb^n + tau pmb_3 right),\ frac<pmb^ -pmb^n> &= frac (pmb_1 + 2pmb_2 + 2pmb_3 + pmb_4) & & end $$

Видео:Линейное дифференциальное уравнение Коши-ЭйлераСкачать

Многошаговые методы

В методах Рунге—Кутта в вычислениях участвуют значения приближенного решения только в двух соседних узлах ( pmb^n ) и ( pmb^ ) — один шаг по переменной ( t ). Линейный ( m )-шаговый разностный метод записывается в виде $$ begin tag frac sum_^m a_i pmb^ = sum_^ b_i pmb(t_, pmb^), quad n = m-1, m, ldots end $$ Вариант численного метода определяется заданием коэффициентов ( a_i ), ( b_i ), ( i = 0, 1, ldots, m ), причем ( a_0 ne 0 ). Для начала расчетов по рекуррентной формуле (13) необходимо задать ( m ) начальных значений ( pmb^0 ), ( pmb^1 ), ( dots ), ( pmb^ ) (например, можно использовать для их вычисления метод Эйлера).

Различные варианты многошаговых методов (методы Адамса) решения задачи с начальными условиями для систем обыкновенных дифференциальных уравнений могут быть получены на основе использования квадратурных формул для правой части равенства $$ begin tag pmb(t_) — pmb(t_n) = int_^<t_> pmb(t, pmb) dt end $$

Для получения неявного многошагового метода используем для подынтегральной функции интерполяционную формулу по значениям функции ( pmb^ = pmb(t_, pmb^) ), ( pmb^n ), ( dots ), ( pmb^ ), т.е. $$ begin tag frac<pmb^ — pmb^n> = sum_^ b_i pmb(t_, pmb^) end $$

Для интерполяционного метода Адамса (15) наивысший порядок аппроксимации равен ( m+1 ).

Для построения явных многошаговых методов можно использовать процедуру экстраполяции подынтегральной функции в правой части (14). В этом случае приближение осуществляется по значениям ( pmb^n ), ( pmb^ ), ( dots ), ( pmb^ ) и поэтому $$ begin tag frac<pmb^ — pmb^n> = sum_^ b_i pmb(t_, pmb^) end $$

Для экстраполяционного метода Адамса (16) погрешность аппроксимации имеет ( m )-ый порядок.

На основе методов Адамса строятся и схемы предиктор–корректор. На этапе предиктор используется явный метод Адамса, на этапе корректора — аналог неявного метода Адамса. Например, при использовании методов третьего порядка аппроксимации в соответствии с (18) для предсказания решения положим $$ frac<pmb^ — pmb^n> = frac (23 pmb^ -16pmb^ + 5pmb^). $$ Для уточнеия решения (см. (17)) используется схема $$ frac<pmb^ — pmb^n> = frac (9pmb^ + 19pmb^ — 5pmb^ + pmb^). $$ Аналогично строятся и другие классы многошаговых методов.

Видео:Решение системы дифференциальных уравнений методом ЭйлераСкачать

Жесткие системы ОДУ

При численном решении задачи Коши для систем обыкновенных дифференциальных уравнений (3), (4) могут возникнуть дополнительные трудности, порожденные жесткостью системы. Локальные особенности поведения решения в точке ( u = w ) передаются линейной системой $$ begin frac

= sum_^ frac (t, w) v + bar(t), quad t > 0. end $$

Пусть ( lambda_i(t) ), ( i = 1, 2, ldots, m ) — собственные числа матрицы $$ begin A(t) = < a_(t) >, quad a_(t) = frac(t, w). end $$ Система уравнений (3) является жесткой, если число $$ begin S(t) = frac <max_|Re lambda_i(t)|> <min_|Re lambda_i(t)|> end $$ велико. Это означает, что в решении присутствуют составляющие с сильно различающимися масштабами изменения по переменной ( t ).

Для численное решения жестких задач используются вычислительные алгоритмы, которые имеют повышенный запас устойчивости. Необходимо ориентироваться на использование ( A )-устойчивых или ( A(alpha) )-устойчивых методов.

Метод называется ( A )-устойчивым, если при решении задачи Коши для системы (3) область его устойчивости содержит угол $$ begin |arg(-mu)| —>

Видео:Дифференциальное уравнение. Формула ЭйлераСкачать

Методы явные и неявные

Дата добавления: 2015-06-12 ; просмотров: 15293 ; Нарушение авторских прав

Процесс формирования математической модели для численного интегрирования обязательно включает этап алгебраизации, который состоит в преобразовании обыкновенных дифференциальных уравнений в алгебраические. Он основан на использовании одного из методов численного интегрирования.

Если задано дифференциальное уравнение

(3.1)

и начальные условия , то очередное значение может быть получено интегрированием (3.1):

(3.2)

Определенный интеграл в (3.2) численно равен площади под кривой на интервале (рис. 3.2).

Приближенно эта площадь может быть вычислена как площадь прямоугольника, высота которого равна значению функции на левой границе интервала или значению на правой границе интервала. Очевидно, площади обоих прямоугольников, ограниченных сверху отрезками 1 и 2 на рис. 3.3, будут тем ближе к точному значению интеграла, чем меньше шаг интегрирования .

Подставив в (3.2) приближенные значения интеграла, можно получить две формулы:

(3.3)

. (3.4)

Выражение (3.3) представляет собой формулу явного метода Эйлера. Называется метод явным потому, что неизвестное значение 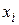может быть непосредственно вычислено по известному значению в предыдущей точке.

Формула (3.4) соответствует неявному методу Эйлера. Здесь в правой части выражения используется неизвестное значение 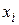, поэтому вычислить его непосредственно по этой формуле нельзя.

Более точное значение интеграла (3.2) дает метод трапеций, которому соответствует отрезок 3 на рис. 3.3. Тогда

. (3.5)

Эта формула относится, очевидно, тоже к неявным.

Для явных методов процедура формирования модели для численного интегрирования ограничивается алгебраизацией исходных дифференциальных уравнений. В частности, формула (3.3) не требует дальнейших преобразований и готова для применения.

Для неявных методов дальнейшие действия зависят от того, какой метод решения системы нелинейных уравнений реализован в данном пакете. Одним из вариантов может быть использование итерационного метода Ньютона, который, как известно, обладает наибольшей скоростью сходимости среди практически применяемых методов, и в котором многократно решается система линеаризованных алгебраических уравнений.

В этом случае реализуется второй этап подготовки математических моделей для неявных методов, который состоит в линеаризации нелинейных алгебраических уравнений, т.е. в разложении нелинейных функций в ряд Тэйлора и сохранении в результате только линейных членов.

Пусть задано нелинейное алгебраическое уравнение

(3.6)

где – вектор переменных.

Разложение (3.6) в ряд Тэйлора с сохранением только линейных членов дает приближенную замену

(3.7)

где –начальное приближение, в качестве которого берутся значения переменных на предыдущем шаге интегрирования;

– неизвестное значение переменной на шаге интегрирования.

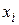
Выражение (3.7) может быть записано как линейное алгебраическое уравнение

,(3.8)

где – вычисляется для известных значений переменных на предыдущем шаге интегрирования;

Таким образом, процесс численного моделирования в общем случае нелинейных систем неявными методами состоит в формировании и решении на каждом шаге интегрирования системы линейных алгебраических уравнений

, (3.9)

которая включает компонентные и топологические уравнения моделируемой схемы. При этом, процедурам алгебраизации и линеаризации подвергаются только компонентные уравнения, так как топологические уравнения всегда линейные алгебраические.

Рассмотрим пример связанный с подготовкой модели для численного решения нелинейного дифференциального уравнения второго порядка

Первым шагом является сведение данного уравнения к задаче Коши, т.е. к системе уравнений первого порядка за счет введения новой переменной :

Явные формулы метода Эйлера имеют вид

Неявные формулы запишутся следующим образом:

Для перехода к матричной записи выполним ряд преобразований:

Здесь ,

Матричная запись имеет вид

.

Формулу (3.7), вообще говоря, необходимо применять итерационно. Решение этого уравнения, найденное для заданного начального приближения , следует использовать в качестве очередного приближения в (3.7) и повторять формирование и решение линейного алгебраического уравнения до тех пор, пока два последовательных приближения не станут близкими с заданной точностью. При численном моделировании можно ограничиться только одной итерацией, выбирая достаточно малый шаг интегрирования и учитывая, что при этом значения переменных на предыдущем шаге являются достаточно хорошим приближением.

3.2.3. Выбор между явными и неявными методами
в процедурах моделирования технических систем

Выбор между явными и неявными методами представляет серьезную проблему. Многие специалисты считают неявные методы более мощным и универсальным инструментом для решения задач моделирования технических систем [23, 15]. Следует, однако, заметить, что лишь недавно появились достаточно мощные и универсальные системы автоматизированного моделирования, такие, как, например, MATLAB или МВТУ [17], допускающие выбор явного или неявного метода решения задачи. Раньше использовались либо явные, либо неявные методы, так как это требовало разных компонентных моделей.

В современных перспективных системах автоматизированного моделирования, пригодных для моделирования технических систем, применяются, как правило, неявные методы численного интегрирования. Неявные методы лучше приспособлены для решения систем дифференциальных и алгебраических уравнений, к тому же они более устойчивы. В результате, несмотря на большие затраты машинного времени на каждом шаге интегрирования, связанные с необходимостью решения СЛАУ, общие затраты могут быть значительно меньше за счет увеличения шага интегрирования и уменьшения общего количества шагов.

Рассмотрим эту особенность неявных методов на примере явного и неявного методов Эйлера [21], определяемых формулами (3.3) и (3.4), соответственно.

Применим указанные формулы для численного интегрирования простейшего линейного дифференциального уравнения

.

Характеристическое уравнение данной динамической системы имеет вид

, или ,

где – постоянная времени системы.

Единственный полюс системы находится в левой полуплоскости, следовательно, исходная система устойчива. Соответственно, любое решение уравнения, при , стремится к нулю.

Разностное уравнение, соответствующее численному решению явным методом Эйлера, запишется как

.

Известно, что условием устойчивости полученного разностного уравнения является

или .

Это означает, что выбор 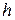может качественно изменить вид решения, превратив устойчивый процесс в неустойчивый.

Таким образом, на шаг интегрирования наложено очевидное ограничение – он не может быть больше постоянной времени системы, иначе дискретная аппроксимация станет неустойчивой. Если система имеет несколько постоянных времени, то подобное ограничение связывает шаг интегрирования с самой маленькой постоянной времени.

Переход к методам более высокого порядка мало меняет картину. Для метода Рунге – Кутты 4-го порядка требование устойчивости ограничивает шаг величиной , или, в более общем виде, , где – максимальное собственное значение матрицы Якоби [29].

Применение неявного метода Эйлера к той же системе дает

,

где ограничение на величину шага выглядит по-другому:

,

что позволяет выбрать шаг любой величины, ориентируясь только на требуемый уровень погрешности.

📽️ Видео

3_04. Неявный алгоритм Эйлера для ОДУСкачать

Дифференциальные уравнения. Задача Коши. Метод Эйлера.Скачать

Пример решения задачи Коши методом Эйлера. Метод Эйлера с пересчетом.Скачать

МЗЭ 2022 Численное решение дифференциальных уравнений Метод Эйлера Ложкин С. А.Скачать

Видеоурок "Системы диф. уравнений. Метод Эйлера"Скачать

3_03. Явный алгоритм Эйлера для ОДУСкачать

Численные методы решения ДУ: метод ЭйлераСкачать

Лекция №1.1 Явная и неявная схемы для уравнения теплопроводностиСкачать

6.4 Явные методы Рунге-КуттыСкачать

6-4. Неявный алгоритм ЭйлераСкачать

Метод Эйлера для дифурСкачать