Построение решений обыкновенных дифференциальных уравнений
Решение дифференциального уравнения 1-го порядка


Простой метод Эйлера реализуется применением на каждом шаге вычислений следующих итерационных выражений:
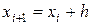
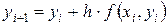
Рассмотрим реализацию метода в MathCADна примере уравнения:
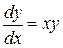
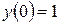
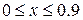
Аналитическое решение известно и имеет вид:

Краткие сведения о составлении программ в MathCAD
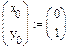
Графиквставляется командой Insert→ Graph→ X-YPlotили клавишей «@».
Для удобства в работе рекомендуется отключить автоматическое вычисление, убрав галочку с опции меню Tools→ Calculate→ AutomaticCalculation. Тогда расчет не будет выполняться в ходе набора программы, а запуститься только после нажатия кнопки Calculate, расположенной на панели инструментов (в виде значка 
Ниже приведена расчетная программа. Повторите её. Получите графики с тем же форматом линий. Формат линий графика можно изменить, открыв с помощью ПК мыши контекстное меню и выбрав Format… → Traces.
Программа для простого метода Эйлера
 |
| Шаг изменения x |
 |
| Число шагов |
 |
| Функция, определяющая производную |
 |
| Задание цикла |
 |
| Задание начальных условий |
 |
| Итерационные уравнения |
| Результаты решения: |
 |
 |
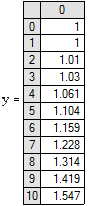 |
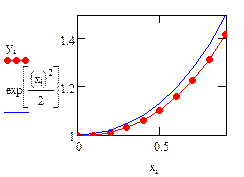 |
Следующая программа реализует модифицированный метод Эйлера. Отличие от простого метода заключается в итерационных уравнениях.
Программа для модифицированного метода Эйлера
 |
| Шаг изменения x |
 |
| Число шагов |
 |
| Функция, определяющая производную |
 |
| Задание цикла |
 |
| Задание начальных условий |
| Итерационные уравнения |
 |
| Результаты решения: |
 |
 |
 |
 |
Метод Рунге-Кутта 4-го порядка используется в тех случаях, когда необходима высокая точность расчетов, недостигаемая методами Эйлера.
Программа для метода Рунге-Кутта
 |
| Шаг изменения x |
 |
| Число шагов |
 |
| Функция, определяющая производную |
| Задание коэффициентов k1, k2, k3, k4 как функций пользователя: |
 |
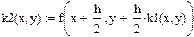 |
 |
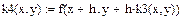 |
 |
| Усредненная функция |
 |
| Задание цикла |
 |
| Задание начальных условий |
 |
| Итерационные уравнения |
| Результаты решения: |
 |
 |
 |
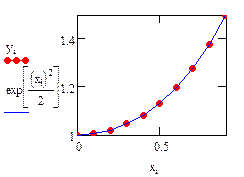 |
Решение дифференциальных уравнений 2-го порядкаметодом Рунге-Кутта.
Подход к реализации метода основан на использовании дополнительной функции 


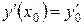
Преобразуем задачу к системе из двух уравнений:


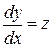

Тогда получим следующее обобщение итерационной схемы:



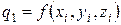
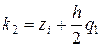




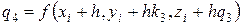
Отметим, что значения на каждом следующем шаге рассчитываются по значениям, полученным на предыдущем. Кроме того, использованы прежние правила «взвешивания» коэффициентов при усреднении.
Пример математической модели с дифференциальным уравнением 2-го порядка
Рассмотрим уравнение колебательного процесса при наличии внешнего периодического воздействия:

где t– время, и искомой является зависимость 
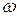
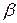
Если 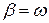

где Aи 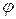
Когда 

В этом случае колебательный процесс слагается из собственных колебаний с частотой 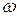
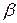
Моделирование резонансных колебаний
Методом Рунге-Кутта найдем решение задачи:

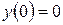


Согласно изложенной выше теории, аналитическое решение уравнения имеет вид:
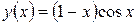
Ниже приведен алгоритм расчета и его реализация в MathCAD.
Программа расчета резонансных колебаний методом Рунге-Кутта
 |
| Шаг изменения x |
 |
| Число шагов |
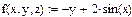 |
| Функция в системе уравнений dy/dx = z и dz/dx = f(x,y,z) |
| Задание коэффициентов как функций пользователя: |
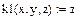 |
 |
 |
 |
 |
 |
 |
 |
| Усредненные функции: |
 |
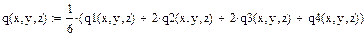 |
 |
| Задание цикла |
 |
| Задание начальных условий |
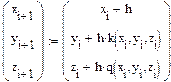 |
| Итерационные уравнения |
 |
| Результаты решения: |
Задание для самостоятельного выполнения
Найти решение уравнения вынужденных колебаний:

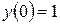
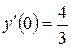
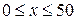
Решение представить в виде графика. Для сравнения привести и график точного решения (также как это было сделано для резонансных колебаний).
- Урок 25. Дифференциальные уравнения в Mathcad
- Метод эйлера для решения дифференциальных уравнений mathcad
- 5.2 Решение дифференциальных уравнений и систем.(Задача Коши и граничные задачи).
- Решение одиночного дифференциального уравнения.
- Численное решение задачи Коши для дифференциальных уравнений и систем.
- Решение граничных задач для обыкновенных дифференциальных уравнений.
- 🔍 Видео
Видео:Решение системы дифференциальных уравнений методом ЭйлераСкачать

Урок 25. Дифференциальные уравнения в Mathcad
Дифференциальные уравнения очень часто применяются для описания изменяющихся процессов. Для начала рассмотрим обыкновенное дифференциальное уравнение (ОДУ):
Аналитическое решение этого уравнения:
Аналитическое решение является точным, и оно быстро дает результат. К сожалению, многие практические дифференциальные уравнения не могут быть решены аналитически. Поэтому нам нужны численные методы.
Метод Эйлера
Наиболее простой метод решения дифференциальных уравнений – метод Эйлера. Это старый метод, легкий для понимания и программирования.
Вычисляем изменения, шаг за шагом:
Сравнение результата и точного решения:
Заметьте, что решение методом Эйлера немного отличается от точного решения, и с ростом аргумента эта разница увеличивается. Уменьшить ошибку можно, если увеличить число шагов.
Блок решения ОДУ
Mathcad содержит все главные решатели дифференциальных уравнений. Их можно найти в меню Функции –> Дифференциальные уравнения. В этом уроке мы рассмотрим самый важный из них. Он прост в использовании и точен. Такой метод сочетает использование блока решения и функцию odesolve(). Перед решением определим:
Все вхождения зависимой переменной c в блоке решения записываются как функции независимой переменной, т.е. как c(t). Есть только одно исключение – запись слева от команды odesolve().
Решение этим методом и аналитическое решение близки. Этот же результат можно получить, записав производную через штрих с помощью [Ctrl+’]:
Пример: сердце и артерии
Работа сердца похожа на работу поршневого насоса: оба они расширяются и сжимаются, клапаны на входе и выходе позволяют течь только в одном направлении. Впускной клапан открывается, когда камера расширяется и позволяет крови попасть в сердце из вены. При сжатии камеры впускной клапан закрывается, и кровь выбрасывается в артерию. Выпускной клапан закрывается, когда камера начинает расширяться.
Пульсация потока уменьшается расширением и сжатием эластичных стенок артерий.
Перепады давления возле легких низки: примем, что избыточное давление в точках A и B равно нулю. Центральным элементом являются артерии, изменение объема которых определяются разницей входного и выходного потоков:
Предположим, что объем сердца изменяется во времени по синусоидальному закону, но кровь выпускается только в течение положительной полуволны:
График для восьми ударов:
Средний поток – это интеграл объема в течение одного удара, деленный на время удара:
Расширение артерий зависит от эластичности стенок и их геометрии, но мы не будем анализировать это здесь. Предположим, что объем линейно зависит от избытка давления:
Чем эластичнее стенки, тем больше значение k. Определим три значения:
Разность давлений следует из:
Баланс объемов артерий:
получаем дифференциальное уравнение для давления:
Решим его таким же образом, как и предыдущее, с той разницей, что k передадим в блок решения как параметр:
Максимумы давления зависят от эластичности артерий – чем больше эластичность, тем меньше давление:
Здесь мы использовали для примера одно дифференциальное уравнение первого порядка, но Mathcad этим не ограничивается.
Резюме
- Обыкновенное дифференциальное уравнение содержит два вида переменных: зависимые (y(x)) и независимые (x).
- Решение можно получить с помощью блока решения и функции odesolve().
- Используйте оператор дифференцирования или штрих в записи дифференциального уравнения. Штрих вводится с помощью [Ctrl+’].
- Введите необходимые граничные условия (они могут содержать запись производной через штрих).
- Функция odesolve() содержит зависимую переменную и независимую переменную.
- Зависимые переменные записываются как функции от независимых.
- В завершение присвойте выходной переменной функцию odesolve(). Выходная переменная не записывается как функция от независимой переменной.
- Однако, при использовании вывода нужно записывать его как функцию независимой переменной.
Видео:Численное решение задачи Коши методом ЭйлераСкачать

Метод эйлера для решения дифференциальных уравнений mathcad
Электронный курс по MathCAD



5.2 Решение дифференциальных уравнений и систем.(Задача Коши и граничные задачи).
Решение одиночного дифференциального уравнения.
Для численного решения одиночного дифференциального уравнения в MathCAD имеется функция Odesolve, с помощью которой может быть решена как задача Коши для обыкновенного дифференциального уравнения, так и граничная задача. Эта функция входит в состав блока решения и сявляется его заключительным ключевым словом.
Odesolve(x,b,[step]) — Возвращает функцию, которая является решением дифференциального уравнения. Используется в блоке с оператором Given.
x — переменная интегрирования, действительное число
b — конечная точка отрезка интегрирования
step — величина шага по переменной интегрирования (необязательный аргумент)
Замечания:
- Уравнение должно быть линейным относительно старшей производной.
- Число заданных начальных или граничных условий внутри блока должно быть равно порядку уравнения.
- При записи уравнения для обозначения производных функции используйте специальные кнопки с панели Math или ‘ (штрих) — [Ctrl+F7], для знака равенства = [Ctrl+=] (в том числе и для дополнительных условий).
- Конечная точка должна быть больше начальной.
- Не допускаются начальные и граничные условия смешанного типа (f ‘(a)+f(a)=5).
- Искомая функция в блоке дложна быть обязательно с аргументом ( f(x))
 |  |
Численное решение задачи Коши для дифференциальных уравнений и систем.
Для численного решения задачи Коши для дифференциальных уравнений и систем могут быть использованы функции:
rkfixed(y,x1,x2,n,F) — возвращает матрицу решений системы уравнений методом Рунге-Кутта 4-го порядка при фиксированном шаге по x
rkadapt(y,x1,x2,n,F) — ищет решение с переменным шагом ( там, где решение меняется медленнее, шаг увеличивается, а в области быстрого изменения решения шаг функции уменьшается). Возвращается решение с равным шагом. Функция работает быстрее, чем rkfixed
Bulstoer(y,x1,x2,n,F) — дает более точное решение (методом Bulirsch-Stoer)
Агрумкнты вышеуказанных функций:
y — вектор начальных условий
x1,x2 — границы интервала для поиска решения
n — количество точек на интервале
F(x,y) — вектор-функция первых производных
При решении дифференциальных уравнений порядка выше первого (или систем уравнений, выше первого порядка) исходное уравнение (систему) необходимо преобразовать к системе дифференциальных уравнений первого порядка.
В результате работы укзанных функций рассчитывается матрица, количество стобцов которой равно порядку уравнения +1(или сумме порядков уравнений в системе +1), а количество строк равно параметру n. Первый столбец содержит значения независимой переменной, второй — значение функции, третий — для диф. уравнений 2-го порядка — значение производной искомой функции (если решается система двух уравнений 1-го порядка, то третий столбец будет содержать значения второй функции). Для выделения решений (функций или их производных) можно воспользоваться стандартным оператором вывода столбцов матрицы M < >
Если матрица правых частей дифференциальных уравнений почти вырождена, то такие системы называются жесткими. В этом случае решения, возвращаемые функцией rkfixed будет неустойчивым и для решения таких систем необходимо применять функции Stiffb , Stiffr
Stiffb(y,x1,x2,n,F,J) — ищет решение диф. уравнения или системы дифференциальных уравнений методом Bulirsch-Stoer
Stiffr(y,x1,x2,n,F,J) — ищет решение диф. уравнения или системы дифференциальных уравнений методом Rosenbrock
 |
 |
 |















































