Метод эйлера для решения дифференциальных уравнений excel

Введение

Уравнение называется обыкновенным дифференциальным n-го порядка, если F определена и непрерывна в некоторой области и, во всяком случае, зависит от . Его решением является любая функция u(x), которая этому уравнению удовлетворяет при всех x в определённом конечном или бесконечном интервале. Дифференциальное уравнение, разрешенное относительно старшей производной имеет вид

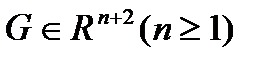
Решением этого уравнения на интервале I=[a,b] называется функция u(x).

Решить дифференциальное уравнение у / =f(x,y) численным методом — это значит для заданной последовательности аргументов х₀, х₁…, х_n и числа у₀, не определяя функцию у=F(x), найти такие значения у₁, у₂,…, у_n, что у_i=F(x_i)(i=1,2,…, n) и F(x₀)=y₀.

Таким образом, численные методы позволяют вместо нахождения функции y=F(x) (3) получить таблицу значений этой функции для заданной последовательности аргументов. Величина h=x_k-x_k-1 называется шагом интегрирования.

Метод Эйлера относиться к численным методам, дающим решение в виде таблицы приближенных значений искомой функции у(х). Он является сравнительно грубым и применяется в основном для ориентировочных расчетов. Однако идеи, положенные в основу метода Эйлера, являются исходными для ряда других методов.

Метод Эйлера для обыкновенных дифференциальных уравнений используется для решений многих задач естествознания в качестве математической модели. Например задачи электродинамики системы взаимодействующих тел (в модели материальных точек), задачи химической кинетики, электрических цепей. Ряд важных уравнений в частных производных в случаях, допускающих разделение переменных, приводит к задачам для обыкновенных дифференциальных уравнений – это, как правило, краевые задачи (задачи о собственных колебаниях упругих балок и пластин, определение спектра собственных значений энергии частицы в сферически симметричных полях и многое другое)

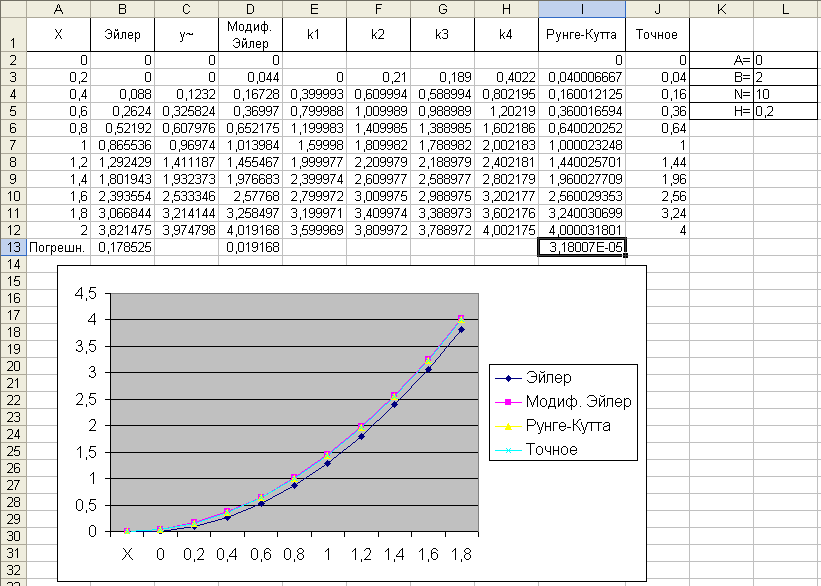
Обзор методов решения в Excel

1.1 Метод Рунге-Кутта четвертого порядка для решения уравнения первого порядка

Идея Рунге-Кута состоит в том, чтобы использовать метод неопределённых коэффициентов. Наиболее употребительным методом Рунге-Кутта решения уравнения первого порядка y’ = F(x,y) (1) является метод четвертого порядка, в котором вычисления производятся по формуле:

Видео:Численное решение обыкновенных дифференциальных уравнений в ExcelСкачать

Метод эйлера для решения дифференциальных уравнений excel

Pers.narod.ru. Обучение. Excel: Решение обыкновенных дифференциальных уравнений (задача Коши)

Решение обыкновенных дифференциальных уравнений (ОДУ) — популярный раздел численных методов, немного теории можно почитать здесь.

В приведённом примере решается задача Коши, то есть, ищется решение дифференциального уравнения первого порядка вида dy/dx = f(x,y) на интервале x ∈ [x₀,x_n] при условии y(x₀)=y₀ и равномерном шаге сетки по x .

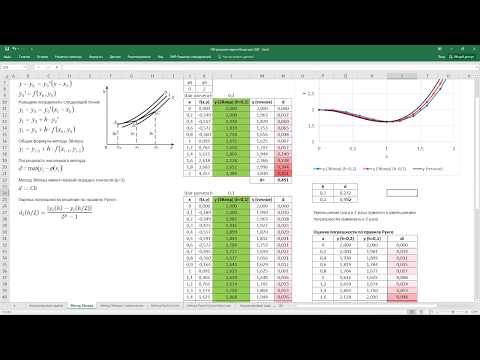
Решение выполняется методами Эйлера, «предиктор-корректор» (он же модифицированный метод Эйлера) и методом Рунге-Кутта 4 порядка точности. Пример может служить образцом для Ваших решений, правда, функцию придётся перепрограммировать несколько раз при различных значениях аргумента — поскольку без применения макросов на VBA Excel не позволяет создать полноценную функцию, которую было бы удобно вызывать с разными значениями аргументов.

Здесь решается уравнение dy/dx = 2x-y+x 2 на интервале [0,2] , начальное значение y(0)=0 , для оценки точности задано также точное решение в виде функции u(x)=x 2 . Оценка погрешности делается в норме L₁ , как и принято в данном случае.

Скачать пример в Excel XP/2003 (28 Кб)

Видео:Метод ЭйлераСкачать

Методическая разработка «Численное решение дифференциальных уравнений методом ломаных Эйлера с использованием редактора электронных таблиц MS Excel»
методическая разработка по информатике и икт на тему

Большинство физических, химических, экономических и прочих процессов описываются дифференциальными уравнениями или системами дифференциальных уравнений. Возникает необходимость получения результатов их решения. И не всегда есть возможность получить точный ответ аналитическим способом.

Поэтому требуются навыки в решении ДУ с использованием численных методов. Один из таких методов – метод ломаных Эйлера. Рассмотрим решение дифференциального уравнения усовершенствованным методом ломаных Эйлера, который имеет большую точность расчетов.

Видео:Численное решение задачи Коши методом ЭйлераСкачать

Скачать:

Видео:Численные методы решения ДУ: метод ЭйлераСкачать

Подписи к слайдам:

Слайд 1
Численное решение дифференциальных уравнений модифицированным методом ломаных Эйлера с использованием редактора электронных таблиц MS Excel Свирина Анастасия Олеговна, методист ИМЦ

Слайд 2
Большинство физических, химических, экономических и прочих процессов описываются дифференциальными уравнениями или системами дифференциальных уравнений. Возникает необходимость получения результатов их решения. И не всегда есть возможность получить точный ответ аналитическим способом. Поэтому требуются навыки в решении ДУ с использованием численных методов. Один из таких методов – метод ломаных Эйлера. Рассмотрим решение дифференциального уравнения усовершенствованным методом ломаных Эйлера, который имеет большую точность расчетов.

Слайд 3
Дано: Начальные условия:

Слайд 4
Даем название столбцам таблицы в соответствии с алгоритмом для решения ДУ аналитически. Создание таблицы

Слайд 5
Длина отрезка равна единице, а шаг разбиения – 0,05. Количество узловых точек – 21. Записываем в таблицу.

Слайд 6
Значение а соответствующее ему значение

Слайд 8
Находим первый аргумент «внешней функции».

Слайд 11
Ищем значение функции в точке, рассчитанной с учетом погрешности.

Слайд 12
Полученный результат умножаем на шаг разбиения.

Слайд 14
Копируем полученные значения по образцу. ( Выделяем значения полей D, E, F, G, H и «растягиваем» на одну строку вниз )

Слайд 15
( Выделяем значения полей C, D, E, F, G, H и «растягиваем» до конца таблицы )

Слайд 16
Искомое приближенное решение:

Слайд 18
При решении данного ДУ аналитически результат будет равен ─ 2,71875 . Вывод: усовершенствованный метод ломаных Эйлера дает более точные результаты в отличие от «классического» метода. Связано это с тем, что производная берется не в начале шага, а как промежуточное или среднее на разных участках одного шага. В процессе использования метода вычисляются несколько производных в разных частях шага, которые впоследствии усредняются. За счет этого точность метода возрастает на порядок.

Слайд 19
Список литературы Эльсгольц Л.Э. «Дифференциальные уравнения и вариационное исчисление» (61 стр.), 1979г. Демидович Б.П. «Сборник задач и упражнений по математическому анализу», 1995г. Тихонов А.Н., Васильева А.Б., Свешников А.Г. «Дифференциальные уравнения» (31 стр.), 1985г.

Видео:Решение ОДУ 1 го порядка в ExcelСкачать

По теме: методические разработки, презентации и конспекты

Урок Информатика и ИКТ Тема: Деловая графика. Построение графиков и диаграмм средствами редактора электронных таблиц Microsoft Excel

Разработка урока и презентация по информатике и ИКТ в 9 кл. по теме: Деловая графика. Построение графиков и диаграмм средствами редактора электронных таблиц Microsoft Excel.

Элективный курс «Исследование информационных моделей с использованием электронных таблиц Microsoft Excel»

Методическая разработка интегрированного урока физика+информатика «Сила трения; определение коэффициента трения скольжения с использованием электронных таблиц Microsoft Excel» — практическая работа для профессии Судоводитель

Интегрированный урок физика+информатикаУрок по физике — повторение материала по теме «Сила трения» с элементом выполнения практической работы; по информатике — закрепление имеющихся навыков рабо.

МЕТОДИЧЕСКАЯ РАЗРАБОТКА ПО ТЕМЕ: «ЭЛЕКТРОННЫЕ ТАБЛИЦЫ MICROSOFT EXCEL»

Методическая разработка представляет собой комплексный заданий, по предмету информатика, для работы в программе MS Excel, входящей в состав пакета прикладных программ Microsoft Office.Данная тем.

Решение задач математического анализа и линейной алгебры средствами электронных таблиц MS Excel

Решение задач математического анализа и линейной алгебры средствами электронных таблиц MS Excel.

Использование электронный таблиц Microsoft Excel при создании дидактического материала.

Тест и кросворд.Тема: «Двигатель внутреннего сгорания&quot.

Интегрированный урок по математике и информатике «Решение задач с помощью уравнений, сводящихся к линейным, с использованием электронных таблиц Ms Excel.»

Урок комплексного применения знаний и умений.

📸 Видео

метод Эйлера для решения ОДУСкачать

6.1 Численные методы решения задачи Коши для ОДУСкачать

Решение системы дифференциальных уравнений методом ЭйлераСкачать

Решение ОДУ:метод ЭйлераСкачать

Метод Эйлера в ексельСкачать

Дифференциальные уравнения. Задача Коши. Метод Эйлера.Скачать

Пример решения задачи Коши методом Эйлера. Метод Эйлера с пересчетом.Скачать

Решение ОДУ: метод Рунге КуттаСкачать

Метод Эйлера. Решение систем ДУСкачать

Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Дифференциальное уравнение. Формула ЭйлераСкачать

Решение ОДУ методом Эйлера (программа)Скачать

Видеоурок "Системы диф. уравнений. Метод Эйлера"Скачать

Численные методы решения ДУ: метод Рунге-КуттаСкачать