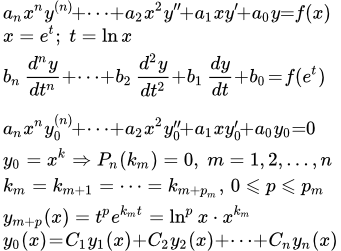Метод эйлера для решения дифференциальных уравнений это

Метод Эйлера: для чего он нужен, порядок действий и упражнения — Наука

Видео:Метод ЭйлераСкачать

Содержание:

В Метод Эйлера Это самая базовая и простая из процедур, используемых для нахождения приближенных численных решений обыкновенного дифференциального уравнения первого порядка, при условии, что известно его начальное условие.

Обыкновенное дифференциальное уравнение (ОДУ) — это уравнение, которое связывает неизвестную функцию одной независимой переменной с ее производными.

Если наибольшая производная, которая появляется в уравнении, имеет степень один, то это обыкновенное дифференциальное уравнение первой степени.

Самый общий способ написать уравнение первой степени:

Видео:Линейное дифференциальное уравнение Коши-ЭйлераСкачать

Что такое метод Эйлера?

Идея метода Эйлера заключается в нахождении численного решения дифференциального уравнения в интервале между X₀ и X_F .

Сначала интервал дискретизируется на n + 1 балл:

Которые получаются так:
Икс_я= х₀+ я

Где h — ширина или шаг подынтервалов:

С начальным условием также можно узнать производную в начале:

Эта производная представляет собой наклон касательной к кривой функции y (x) точно в точке:

Затем делается приблизительный прогноз значения функции y (x) в следующей точке:

Затем была получена следующая приближенная точка решения, которая будет соответствовать:

Процедура повторяется для получения последовательных баллов.

На рисунке, показанном в начале, синяя кривая представляет точное решение дифференциального уравнения, а красная — последовательные приближенные точки, полученные с помощью процедуры Эйлера.

Видео:Решение системы дифференциальных уравнений методом ЭйлераСкачать

Решенные упражнения

Видео:Пример решения задачи Коши методом Эйлера. Метод Эйлера с пересчетом.Скачать

Упражнение 1

я) Пусть дифференциальное уравнение имеет вид:

При начальном условии x = a = 0; Y_к= 1

Используя метод Эйлера, получить приближенное решение Y в координате X = b = 0,5, разбивая интервал [a, b] на n = 5 частей.

Видео:Дифференциальное уравнение. Формула ЭйлераСкачать

Решение

Численные результаты резюмируются следующим образом:

Из чего делается вывод, что решение Y для значения 0,5 составляет 1,4851.

Примечание: для проведения расчетов, Smath studio, бесплатная программа для бесплатного использования.

Видео:Численное решение задачи Коши методом ЭйлераСкачать

Упражнение 2.

II) Продолжая работу с дифференциальным уравнением из упражнения I), найдите точное решение и сравните его с результатом, полученным методом Эйлера. Найдите ошибку или разницу между точным и приблизительным результатом.

Видео:Дифференциальные уравнения. Задача Коши. Метод Эйлера.Скачать

Решение

Точное решение найти не очень сложно. Производная функции sin (x) известна как функция cos (x). Следовательно, решение y (x) будет:

Для выполнения начального условия и (0) = 1 константа C должна быть равна 1. Затем точный результат сравнивается с приблизительным:

Сделан вывод, что в расчетном интервале аппроксимация имеет три значащих цифры точности.

Видео:МЗЭ 2022 Численное решение дифференциальных уравнений. Неявный метод Эйлера. Ложкин С.А.Скачать

Упражнение 3.

III) Рассмотрим дифференциальное уравнение и его начальные условия, указанные ниже:

При начальном условии x₀ = 0; Y₀ = 1

Используйте метод Эйлера, чтобы найти приблизительные значения решения у (х) в интервале х = [0, 1,5]. Используйте шаг h = 0,1.

Видео:МЗЭ 2022 Численное решение дифференциальных уравнений Метод Эйлера Ложкин С. А.Скачать

Решение

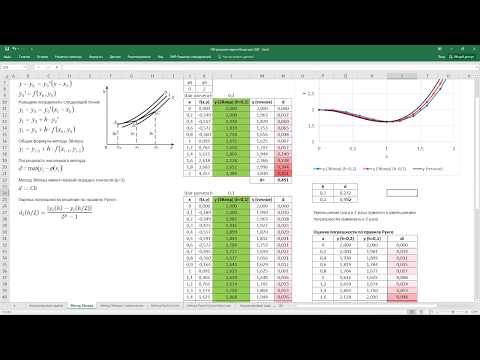
Метод Эйлера очень подходит для использования с электронной таблицей. В этом случае мы будем использовать электронную таблицу геогебра бесплатная и бесплатная программа.

В электронной таблице на рисунке показаны три столбца (A, B, C), первый — это переменная Икс , второй столбец представляет переменную Y, а третий столбец — производная Y ‘.

Строка 2 содержит начальные значения Икс, Y, Y ‘ .

Шаг значения 0,1 помещен в ячейку абсолютного положения ($ D $ 4).

Начальное значение y0 находится в ячейке B2, а y1 — в ячейке B3. Чтобы вычислить y₁ используется формула:

Эта формула электронной таблицы будет иметь вид B3: = B2 + $ D $ 4 * C3.

Точно так же y2 будет в ячейке B4, и его формула показана на следующем рисунке:

На рисунке также показан график точного решения и точки A, B,…, P приближенного решения по методу Эйлера.

Видео:Численные методы решения ДУ: метод ЭйлераСкачать

Ньютоновская динамика и метод Эйлера

Классическая динамика была разработана Исааком Ньютоном (1643 — 1727). Первоначальная мотивация Леонарда Эйлера (1707 — 1783) к разработке своего метода заключалась именно в решении уравнения второго закона Ньютона в различных физических ситуациях.

Второй закон Ньютона обычно выражается в виде дифференциального уравнения второй степени:

куда Икс представляет положение объекта в момент т. Указанный объект имеет массу м и подвергается силе F. Функция F связана с силой и массой следующим образом:

Для применения метода Эйлера требуются начальные значения времени. т, скорость v и положение Икс.

В следующей таблице объясняется, как, начиная с начальных значений t1, v1, x1, можно получить приближение скорости v2 и положения x2 в момент t2 = t1 + Δt, где Δt представляет небольшое увеличение и соответствует шагу в методе Эйлер.

Видео:Видеоурок "Системы диф. уравнений. Метод Эйлера"Скачать

Упражнение 4.

IV) Одна из фундаментальных проблем механики — это проблема блока массы M, привязанного к пружине (или пружине) с постоянной упругостью K.

Второй закон Ньютона для этой проблемы будет выглядеть так:

В этом примере для простоты мы возьмем M = 1 и K = 1. Найдите приблизительные решения для положения Икс и скорость v методом Эйлера на временном интервале [0, π / 2], разбивая интервал на 12 частей.

Возьмите 0 в качестве начального момента, начальную скорость 0 и начальное положение 1.

Видео:Метод Эйлера. Решение систем ДУСкачать

Решение

Численные результаты представлены в следующей таблице:

Также отображаются графики положения и скорости между временами от 0 до 1,44.

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Предлагаемые упражнения для дома

Видео:5 Численное решение дифференциальных уравнений Part 1Скачать

Упражнение 1

Используйте электронную таблицу, чтобы найти приближенное решение с помощью метода Эйлера для дифференциального уравнения:

y ’= — Exp (-y) с начальными условиями x = 0, y = -1 в интервале x = [0, 1]

Начните с шага 0,1. Постройте результат.

Видео:метод Эйлера для решения ОДУСкачать

Упражнение 2.

Используя электронную таблицу, найдите численные решения следующего квадратного уравнения, где y является функцией независимой переменной t.

y ’’ = -1 / y² с начальным условием t = 0; и (0) = 0,5; у ‘(0) = 0

Найдите решение на интервале [0,5; 1.0] с шагом 0,05.

Постройте результат: y vs t; y ‘vs t

Видео:Численное интегрирование методом ЭйлераСкачать

Ссылки

1. Метод Эрлера Взято с wikipedia.org
2. Решатель Эйлера. Взято с en.smath.com

Американский флаг: история и значение

25 песен о любви, которые заставят вас плакать

Видео:Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Метод эйлера для решения дифференциальных уравнений это

Дифференциальным уравнением первого порядка называется уравнение вида F(x,y,у’)=0 или у’=f(x,y). Функция y(x), при подстановке которой уравнение обращается в тождество, называется решением дифференциального уравнения.

Рассмотрим несколько численных методов решения дифференциальных уравнений первого порядка. Описание численных методов приводится для уравнения в виде у’=f(x,y).

Рассмотрим два варианта вывода расчетных формул

Видео:6.1 Численные методы решения задачи Коши для ОДУСкачать

Дифференциальное уравнение Эйлера и методы его решения

Более общее уравнение Эйлера имеет вид:
.
Это уравнение подстановкой t = ax+b приводится к более простому виду, которое мы и будем рассматривать.

Видео:ШОК! Решение ДУ методом Эйлера! ПОХИЩЕНИЕ С СЮРПРИЗОМ!Скачать

Приведение дифференциального уравнения Эйлера к уравнению с постоянными коэффициентами.

Рассмотрим уравнение Эйлера:
(1) .
Оно сводится к линейному уравнению с постоянными коэффициентами подстановкой:
x = e t .
Действительно, тогда
;
;
;

;
;
.

Таким образом, множители, содержащие x m , сокращаются. Остаются члены с постоянными коэффициентами. Однако на практике, для решения уравнений Эйлера, можно применять методы решения линейных ДУ с постоянными коэффициентами без использования указанной выше подстановки.

Решение однородного уравнения Эйлера

Рассмотрим однородное уравнение Эйлера:
(2) .
Ищем решение уравнения (2) в виде
.
;
;
.
.
Подставляем в (2) и сокращаем на x k . Получаем характеристическое уравнение:
.
Решаем его и получаем n корней, которые могут быть комплексными.

Рассмотрим действительные корни. Пусть k_i – кратный корень кратности m . Этим m корням соответствуют m линейно независимых решений:
.

Рассмотрим комплексные корни. Они появляются парами вместе с комплексно сопряженными. Пусть k_i – кратный корень кратности m . Выразим комплексный корень k_i через действительную и мнимую части:
.
Этим m корням и m комплексно сопряженным корням соответствуют 2 m линейно независимых решений:
;
;
.
.

После того как получены n линейно независимых решений, получаем общее решение уравнения (2):
(3) .

Примеры

Решение неоднородного уравнения Эйлера

Рассмотрим неоднородное уравнение Эйлера:
.
Метод вариации постоянных (метод Лагранжа) также применим и к уравнениям Эйлера.

Сначала мы решаем однородное уравнение (2) и получаем его общее решение (3). Затем считаем постоянные функциями от переменной x . Дифференцируем (3) n – 1 раз. Получаем выражения для n – 1 производных y по x . При каждом дифференцировании члены, содержащие производные приравниваем к нулю. Так получаем n – 1 уравнений, связывающих производные . Далее находим n -ю производную y . Подставляем полученные производные в (1) и получаем n -е уравнение, связывающее производные . Из этих уравнений определяем . После чего интегрируя, получаем общее решение уравнения (1).

Пример

Неоднородное уравнение Эйлера со специальной неоднородной частью

Рассмотрим уравнение Эйлера со специальной неоднородной частью:
(4)
,
где – многочлены от степеней и , соответственно.

Наиболее простой способ решения такого уравнения заключается в том, чтобы сделать подстановку
,
и решать линейное уравнение с постоянными коэффициентами со специальной неоднородной частью.

Автор: Олег Одинцов . Опубликовано: 14-08-2013 Изменено: 24-10-2020