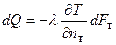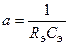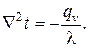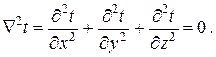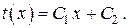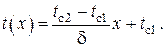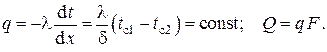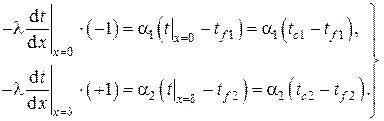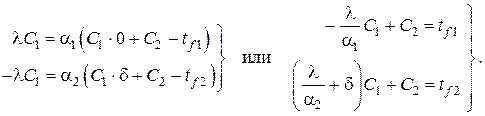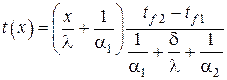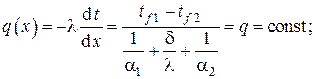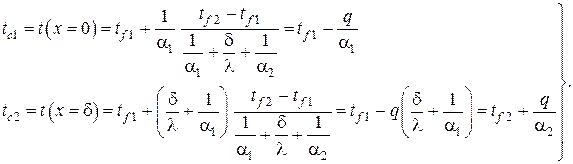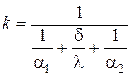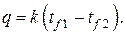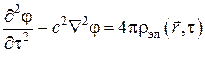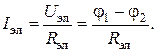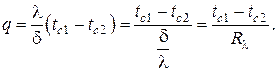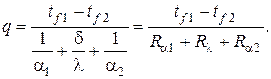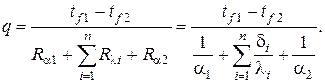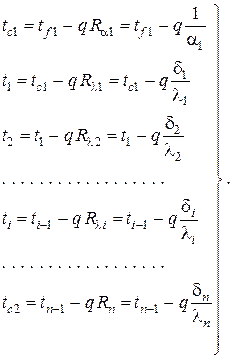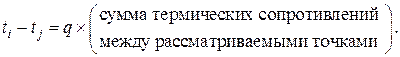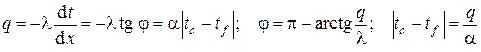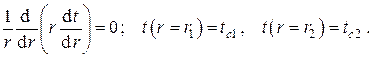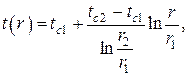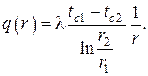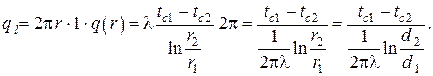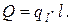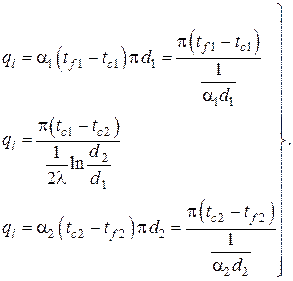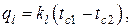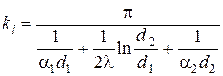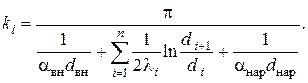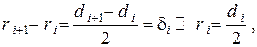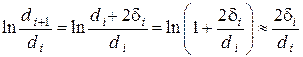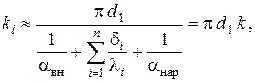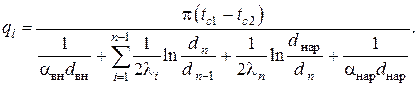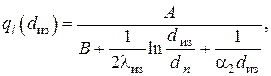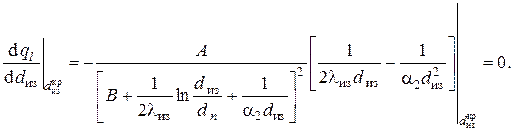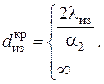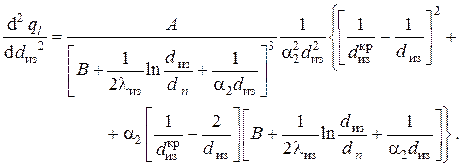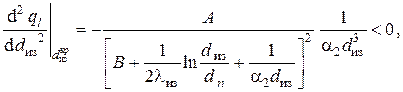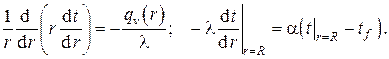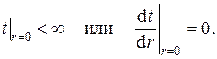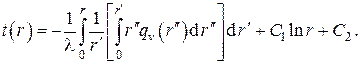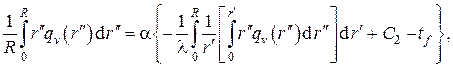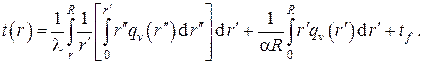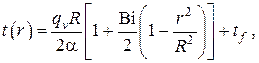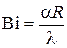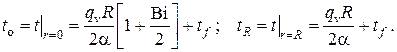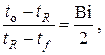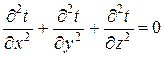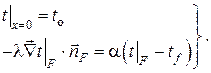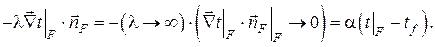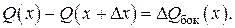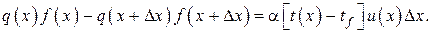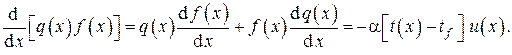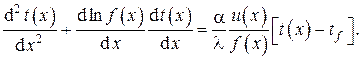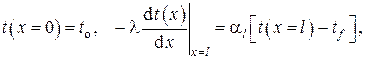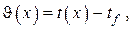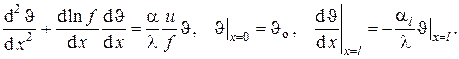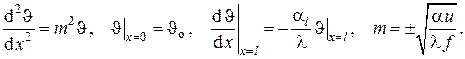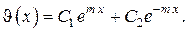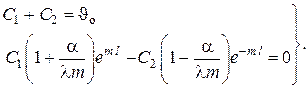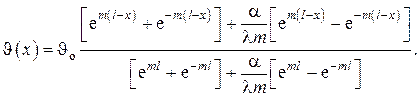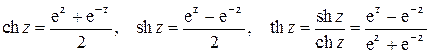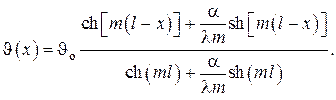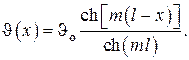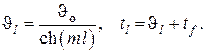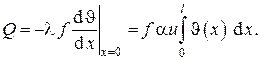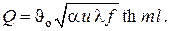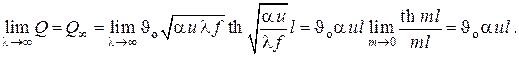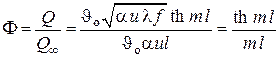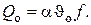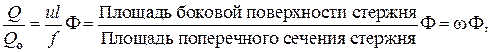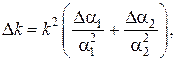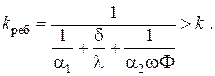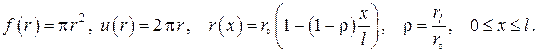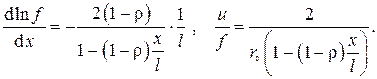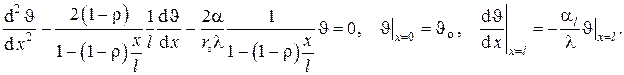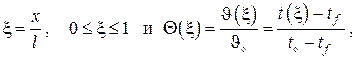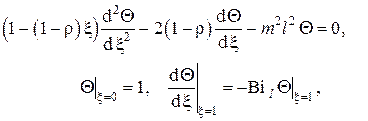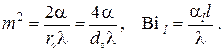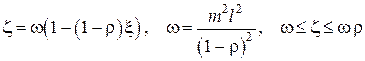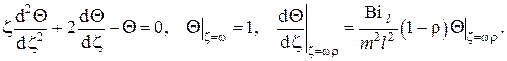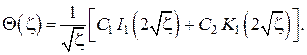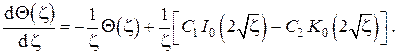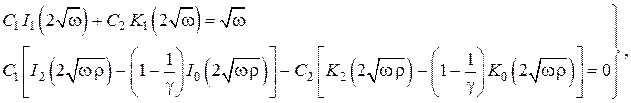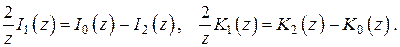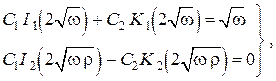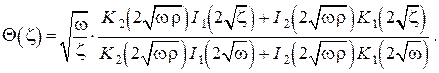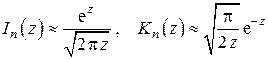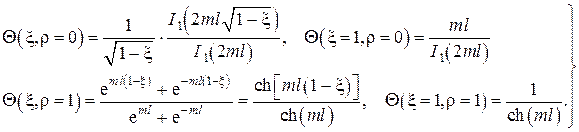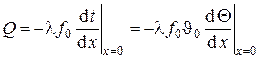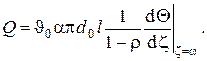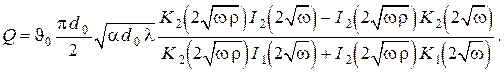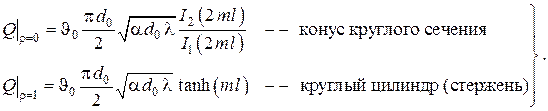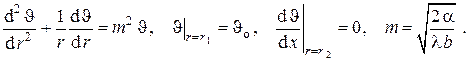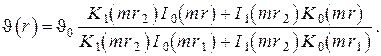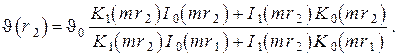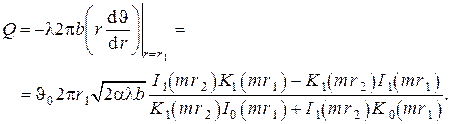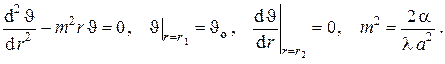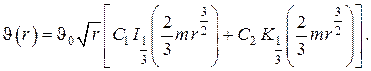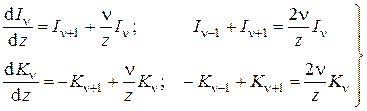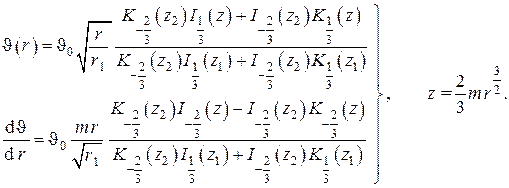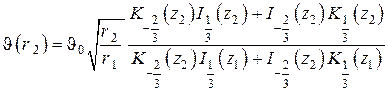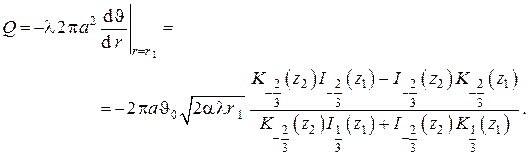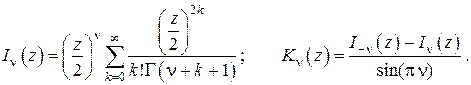Видео:Метод контурных токов - Теория и задачаСкачать

§ III.7. МЕТОД ЭЛЕКТРОТЕПЛОВОИ АНАЛОГИИ
Наиболее удобным и достаточно совершенным методом расчета стационарных температурных полей является метод электротепловой аналогии. Этот метод основан на аналогии математической записи двух разных физических явлений: теплопроводности и электропроводности. Этой аналогией легко воспользоваться для воспроизведения теплового процесса электрическим. Электрическим процессом легче управлять, за ним просто наблюдать и измерять все его параметры. Поэтому удобно именно таким процессом воспроизводить явление теплопроводности, которое само такими достоинствами не обладает. Основа аналогии между этими двумя явлениями состоит в следующем.
Передача тепла теплопроводностью подчиняется закону Фурье, согласно которому
Передача электричества в электропроводящей среде определяется законом Ома
В этих формулах RT и R3 — тепловое и электрическое сопротивления, a At и AU — перепады температур и электрических напряжений.
Из полного соответствия математической записи этих двух законов следует, что если взять геометрически подобный сечению стены лист из электропроводящего материала, то закономерности передачи электричества через него и передачи тепла через стену будут пол-
Ностью аналогичны (рис. III. 19). При этом будет иметь место следующее соответствие между характеристиками, определяющими эти два процесса (табл. III.1).
Между перепадом температур At на границах стенки и перепадом электрических потенциалов AU на соответствующих границах электропроводящего листа может быть произвольное соотношение, которое определит масштаб температур Т, в К/ед-потенц.:
Соотношение между тепловыми RT и электрическими R3 сопротивлениями также может быть произвольным. Оно определяет масштаб сопротивлений Тц в —
Из уравнений теплопроводности и электропроводности следует, что при наперед заданных значениях масштабов сопротивлений и температур масштаб тепловых потоков, Вт/А [(ккал/ч)/А],
Если в уравнение теплопроводности (III.65) подставить значения величин, выраженные через соответствующие масштабы в виде At = = MtAU; RT — тц Ra; q = TnqI, то можно убедиться в полной его тождественности уравнению электропроводности (II 1.66) именно при такой зависимости между масштабами, как (II 1.70). Действительно,
Способ определения масштабов характеристик аналогичных процессов полностью совпадает со способом, применяемым в теории подобия для вывода критериев подобия.
Температурное поле стены с равномерно распределенными параметрами воспроизводится на модели электрическим полем также с равномерно распределенными параметрами. Поэтому, измерив значения потенциала в отдельных точках модели и построив электрическое поле в форме линий равных потенциалов, можно принять его за температурное поле в виде изотерм в стене. Для пересчета электрических потенциалов в температуры нужно воспользоваться масштабом Т(. Обычно для расчета на модели удобно пользоваться условными единицами потенциала, например, в процентах от произвольно принятого полного перепада.
Измерение или расчет силы тока в любом сечении электрической модели позволяет определить с помощью масштаба Т9 величину соответствующих потоков тепла.
Задача расчета может состоять в определении сопротивления теплопередаче сложного элемента. Оно может быть определено измерением на модели соответствующих электрических сопротивлений с последующим их пересчетом с помощью масштаба сопротивлений Т%. Подобным образом с помощью электромодели могут быть определены факторы формы элементов ограждений!
Геометрически подобные электропроводящие среды, на которых воспроизводится температурное поле, в теории методов аналогий называют «геометрическими аналогами». С их помощью наиболее просто воспроизводить температурные поля любой конфигурации однородных конструкций с граничными условиями первого рода. Разработаны
Приемы воспроизведения на «геометрических аналогах» полей с неоднородными включениями при сложных граничных условиях. В качестве электропроводящей среды обычно используют электропроводящую бумагу, фольгу, электролит и др. Для сложных случаев расчета подробное изложение метода с использованием геометрических аналогов можно найти в [III.2].
Расчет температурных полей со сложными включениями, с граничными условиями III рода и другими осложняющими задачу условиями удобнее проводить на электрических цепях. Модель в виде электрической цепи воспроизводит тепловую сетку, построение которой дано при рассмотрении метода сеток в § II 1.6.
В электрической цепи сосредоточенные электрические сопротивления, соединяющие ее узлы, воспроизводят сосредоточенные тепловые сопротивления, соединяющие узлы тепловой сетки (рис. III.20). Здесь также сохраняется полная аналогия математических записей процессов теплопередачи в тепловой сетке и электропередачи в электрической цепи. Поэтому рассмотренные выше соответствия между основными характеристиками процессов и масштабные соотношения остаются справедливыми и для способа воспроизведения темпера-fypHorp поля на электрических цепях. Особенность состоит в том, что под RT и R3 в этом случае надо подразумевать значения сосредоточенных сопротивлений, а под А? и Ш — значения перепадов температур и напряжений между узлами тепловой и электрической сеток.
Для расчетов удобно пользоваться специальными моделями — сетками заводского изготовления — электроинтеграторами ЭИ-12, УСМ и др. (рис. II 1.21). Основными элементами в них являются магазины сопротивлений, которые позволяют набрать между узлами сетки сопротивления нужной величины. На приборе есть специальные устройства, позволяющие задать определенное напряжение или
Определенной силы ток в любой узел сетки и замерить электрические J потенциалы во всех узлах сетки. Наличие таких устройств на электроинтеграторе позволяет решать на нем задачи стационарной теплопередачи практически любой сложности. Подробнее с этими устройствами и способами расчета на них можно познакомиться в III 1.2].
Видео:6.1. Электродинамика РЭ. Основные методы.Скачать

Электротепловая аналогия
Явления теплопроводности и электропроводности описываются следующими уравнениями:
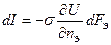
где dQ и dI – элементарные потоки теплоты и электричества, прошедшие в единицу времени через площадки dFт, dFэ в направлении нормалей nт и nэ; U и Т – электрический потенциал и температура; l и s — коэффициенты теплопроводности и электропроводности.
В случае двумерных стационарных задач тепло- и электропроводности и независимых от температуры параметрах l и s соответствующие дифференциальное уравнения имеют вид:
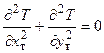
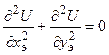
Эти уравнения имеют одинаковую структуру. Аналогичные явления должны протекать в геометрически подобных системах. Граничные условия также описываются аналогичными соотношениями.
Þ — grad T = DT/(l/a) = DT/lт – для тепловой задачи
— grad U = DU/lэ – для электрической задачи.
Записав уравнения и граничные условия в безразмерной форме, получим тождественные уравнения.
Вывод: таким образом, видим, что распределение температуры и электрического потенциала являются подобными, то есть имеет место аналогия.
При исследовании нестационарных процессов для одномерных областей исходные дифференциальное уравнения тепло- и электропроводности имеют вид
Скорость протекания процессов зависит от а и 1/RэCэ,
где Rэ — электрическое сопротивление на единицу длины;
Cэ — электрическая емкость на единицу длины.
Эти коэффициенты, как и коэффициент температуропроводности, не должны зависеть от температуры.
Из уравнений (1) и (2) следует, что аналогия устанавливается, если выполняется условие:
Изменение теплового потока пропорционально изменению теплоемкости системы и изменению температуры:
Изменение электрическое тока пропорционально емкости и изменению напряжения
Следовательно, в модели теплоемкости могут быть воспроизведены соответствующими электрическими емкостями. Таким образом, можно моделировать процессы теплопроводности на электрических моделях.
При разработке электрических моделей, имитирующих процессы теплопроводности, применяются два способа:
1) электрические модели повторяют геометрию оригинальной тепловой системы и изготовляются из материала с непрерывной проводимостью (электропроводящее тело или жидкий электролит) – модели с непрерывными параметрами процесса;
2) электрические модели с сосредоточенными параметрами процесса. В них тепловые системы заменяются моделирующими электрическими цепями. Также модели применяются для наиболее сложных явлений.
Для изготовления моделей с непрерывными параметрами используются тонкие листовые электропроводящие материалы. Геометрия модели в точности воспроизводит геометрию исследуемой области. Получить распределение температуры экспериментально весьма затруднительно. Поэтому исследование проводят на модели. Для измерения напряжения используется контактный зонд с нулевым прибором.
Рассмотрим электрическую модель с сосредоточенными параметрами. В этом случае исследуемая тепловая область делится на ряд элементарных объемов. Тем самым исходные дифференциальные уравнения и уравнения, описывающие условия однозначности, заменяются уравнениями в конечных разностях. Моделирующая электрическая цепь представляется в виде отдельных электрических сопротивлений, имитирующих свойства элементов тепловой области. Используются проволочные модели (из реостатного провода).
Для моделирования нестационарного теплового состояния используются RC цепи.
































Теплоемкости отдельных слоев воспроизводиться электрическими емкостями с1 и с2. Термические сопротивления поверхности моделируются сопротивлением Ra.
Электрическое моделирование получило широкое развитие. Применяя специальные нелинейные элементы (сопротивления) можно имитировать нелинейные граничные условия (теплообмен излучением).
Тепловая схема замещения. Тепловой закон Ома. Распределенные в пространстве теплофизические параметры заменяются сосредоточенными.
Дата добавления: 2021-09-07 ; просмотров: 54 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:Измерение электрической проводимостиСкачать

Глава III. РЕШЕНИЕ ЗАДАЧ СТАЦИОНАРНОЙ
ТЕПЛОПРОВОДНОСТИ
В энергетике, в практике центрального отопления, водоснабжения и т.п. часто встречаются стационарные режимы теплопроводности. В этом случае все функции в уравнении теплопроводности и в граничных условиях не зависят от времени τ. Уравнение теплопроводности переходит тогда в уравнение Пуассона и принимает вид
Рассмотрим далее некоторые часто встречающиеся в энергетике, химической и металлургической промышленности, строительной теплотехнике и т.д. задачи стационарной теплопроводности.
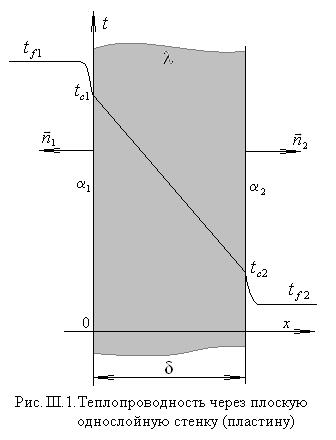
1.Стационарная теплопроводность в плоской однослойной однородной бесконечной пластине[3] без внутренних источников тепла при однородных граничных условиях I рода на противоположных плоскостях
В этом случае дифференциальное уравнение теплопроводности представляет собой уравнение Лапласа (в декартовых координатах)
Граничные условия в данной задаче выглядят следующим образом
Используя самые общие соображения симметрии задачи – однородность по отношению к выбору начала координат (точка 0) и параллельному переносу оси (0,x) а также изотропность, т.е. инвариантность задачи по от-ношению к поворотам на любой угол вокруг выбранной оси (0,x), можно однозначно заключить, что изотермические поверхности в данной задаче будут представлять собой плоскости, перпенди-кулярные оси x, т.е. искомая функция температуры 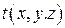
общее решение которого представляется линейной функцией
Произвольные постоянные 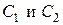
Плотность теплового потока через стенку вычисляется на основании закона Био-Фурье . В одномерном случае имеем
2.Стационарная теплопроводность в плоской однослойной однородной бесконечной пластине без внутренних источников тепла при однородных граничных условиях III рода на противоположных плоскостях
В этом случае дифференциальное уравнение теплопроводности остаётся тем же, что и в предыдущем примере, т.е. с тем же общим решением в виде линейной зависимости , однако поиск произвольных постоянных C1 и C2 должен осуществляться с использованием граничных условий III рода , которые в данном случае принимают вид
Используя общее решение , получаем систему алгебраических уравнений для нахождения C1 и C2 (обозначения см. на рис. 3)
Находя отсюда C1 и C2 и подставляя в находим распределение температур в однослойной плоской стенке
– плотность теплового потока
– температуры граничных плоскостей пластины
носит название коэффициента теплопередачи через плоскую стенку. С учётом этого определения
Отступление. Электротепловая аналогия (ЭТА)
По определению, аналогичныминазываются различные физические явления, описываемые одинаковыми дифференциальными уравнениями с одинаковыми условиями однозначности (с возможными различными обозначениями).
В качестве примера аналогичных явлений можно привести математические записи закона тяготения Ньютона и закона Кулона для случая взаимодействия двух противоположно заряженных электрических зарядов.
Идея электротепловой аналогии (ЭТА) состоит в том, что дифференциальное уравнение Дж. К. Максвелла для электрического потенциала в сплошной электропроводящей среде
и уравнение теплопроводности по виду совпадают друг с другом с точностью до обозначений для стационарных задач
Стационарное уравнение для электрического потенциала φ базируется на известном законе Ома
Совершенно аналогичным образом стационарное уравнение теплопроводности базируется на аналогичном линейном законе Био-Фурье , которое в линейных одномерных задачах для однородных сред имеет вид (см. )
Выражение также имеет вид закона Ома для трёх последовательно соединённых электрических сопротивлений
Здесь 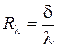
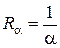
По аналогии с теорией постоянного электрического тока термическое сопротивление теплопроводности 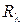
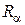
Таким образом, в соответствии с ЭТА, задача стационарной теплопроводности через плоскую однослойную стенку при граничных условиях III рода (см. рис. 3) сводится к эквивалентной задаче расчёта электрической цепи, составленной из трех последовательно соединённых электрических сопротивлений.
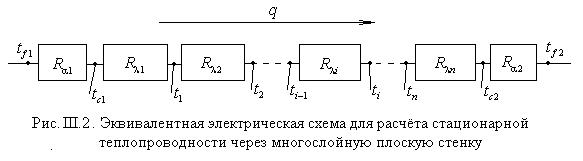
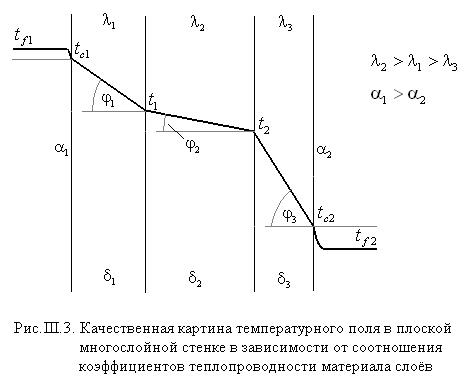
3.Стационарная теплопроводность в плоской многослойной бесконечной пластине без внутренних источников тепла при однородных граничных условиях III рода на противоположных плоскостях
Электротепловая аналогия (ЭТА) позволяет легко осуществить обобщение предыдущей задачи на многослойную плоскую стенку при граничных условиях III рода. На рис. III.2 представлена эквивалентная электрическая схема данной задачи.
Используя законы постоянного электрического тока, в частности, правило вычисления полного сопротивления как суммы последовательно соединённых сопротивлений и одинаковость постоянного электрического тока во всех сопротивлениях, получаем
Вспомнив, что в теории постоянного электрического тока падение напряжения на сопротивлении равно произведению тока и сопротивления, в тепловой задаче аналогичным образом имеем
Естественно, что возможны также другие (многочисленные) комбинации связи температур в различных точках эквивалентной схемы. В любом случае температуры в точках i и j связаны между собой соотношением
Замечание
Из записи закона Био-Фурье и гипотезы Ньютона-Рихмана для одномерного случая с учётом геометрического смысла первой производной
следует, что при заданной плотности теплового потока тангенс угла наклона температурной прямой в координатах 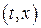
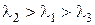
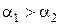
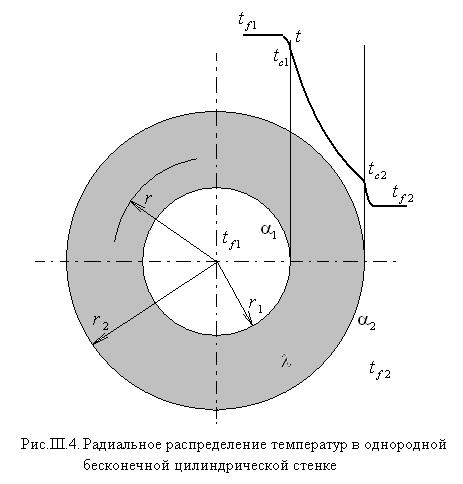
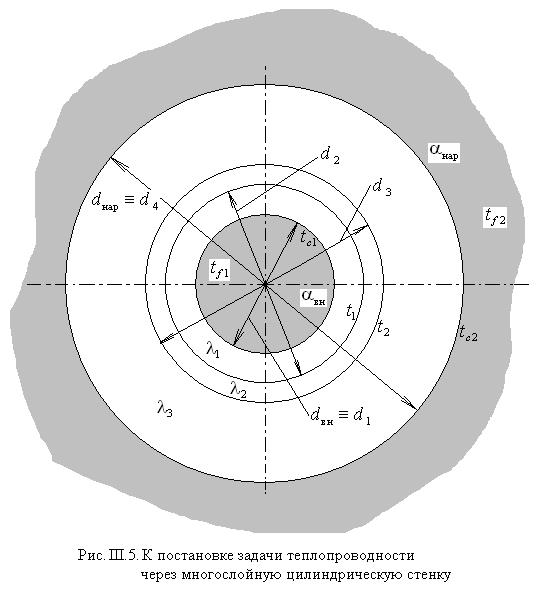
4.Стационарная теплопроводность в бесконечной однослойной цилиндрической стенке без внутренних источников тепла при однородных граничных условиях I рода на противоположных поверхностях
В предположении аксиальной и угловой симметрии задачи её математическая постановка выглядит следующим образом
Решение этой задачи с учётом граничных условий есть
т.е. стационарное радиальное распределение температур в цилиндрической стенке представляется не линейной, а логарифмической зависимостью.
Тогда плотность теплового потока в соответствии с определением радиальной составляющей градиента температур будет по определению равна
Здесь следует отметить, что в случае цилиндрической стенки плотность теплового потока 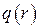
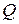
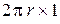
Величина 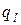
На рис. III.4 приведено графическое представление решаемой задачи.
5.Стационарная теплопроводность в бесконечной однослойной цилиндрической стенке без внутренних источников тепла при однородных граничных условиях III рода на противоположных поверхностях
Используя граничные условия III рода в расчёте на единицу длины трубы, имеем систему алгебраических уравнений
Воспользовавшись ЭТА, легко находим
есть по определению коэффициент теплопередачи для цилиндрической стенки.
Обобщение на многослойную цилиндрическую стенку в соответствии с ЭТА осуществляется стандартным образом и даёт следующее выражение для коэффициента теплопередачи
Графическое представление задачи стационарной теплопроводности через многослойную цилиндрическую стенку с соответствующими обозначениями приведено на рис. III.5.
Заметим, что в случае тонкой цилиндрической стенки, т.е. если
в линейном приближении
т.е. цилиндрическая задача переходит в плоскую .
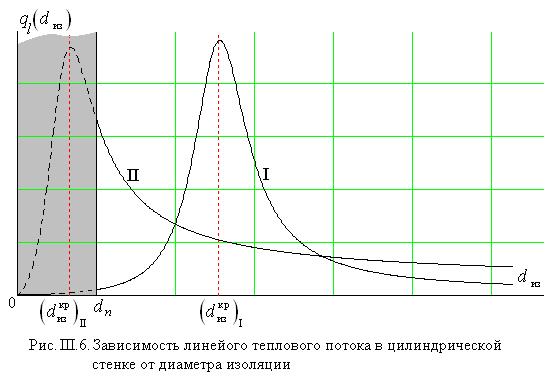
6.Критический диаметр изоляции
Рассмотрим задачу стационарной теплопроводности через многослойную цилиндрическую стенку , , предположив возможность изменения толщины (диаметра) внешнего слоя, контактирующего с внешней текучей средой. Здесь подразумевается технология теплоизоляции цилиндрических труб с целью уменьшения теплопотерь.
Выделив явным образом внешний слой в , для линейного теплового потока имеем
Предполагая здесь постоянными все величины, кроме 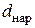
где использованы общепринятые обозначения для диаметра изоляции, теплопроводности материала изоляции и коэффициента теплоотдачи с наружной поверхности.
Легко видеть, что изменение диаметра изоляции двояким образом влияет на теплопотери: логарифмическое слагаемое в знаменателе возрастает с увеличением диаметра изоляции, приводя к уменьшению теплопотерь, в то время как третье слагаемое в знаменателе уменьшается, вызывая тенденцию к увеличению теплосъёма. Это объясняется тем, что увеличение толщины изоляции приводит к увеличению термического сопротивления теплопроводности, но это же ведёт к увеличению наружной поверхности теплосъёма. Очевидно, что эти два противоборствующих фактора должны привести к наличию экстремума функции . Следуя стандартной процедуре поиска координаты экстремума функции одной независимой переменной, имеем
Это алгебраическое уравнение имеет два корня
Тип экстремальной точки (максимум или минимум) определяется знаком второй производной, которая с учётом равна
Подставив сюда 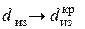
т. е. при 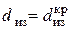
На рис. III.6 изображена зависимость 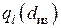
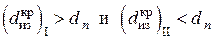
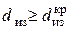
Эффект увеличения теплопотерь при нанесении теплоизоляции в определённых пределах толщин изоляционных слоёв является, конечно, вредным, однако этот эффект проявляется весьма редко в строительной и энергетической практике, где диаметры цилиндрических поверхностей (труб) в большинстве случаев значительны. В случае же цилиндрических поверхностей малого диаметра (капиллярные трубки, электрические провода) критический диаметр изоляции зачастую превышает диаметр изолируемой поверхности, и эффект этот может быть использован и используется для увеличения теплосъёма, в частности, в обмотках электрических агрегатов большой мощности (электродвигатели, электрогенераторы).
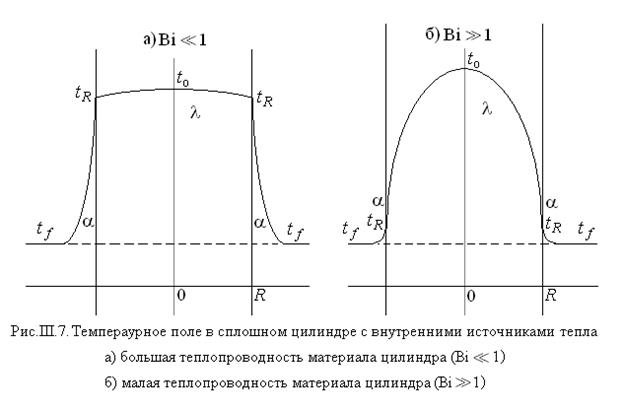
7.Стационарное температурное поле в бесконечном однородном сплошном цилиндре с внутренними источниками тепла с цилиндрической симметрией при однородных граничных условиях III рода на наружной поверхности
В данном случае математическая постановка задачи (см. ) выглядит следующим образом (схема задачи представлена на рис. III.7)
В качестве второго граничного условия в силу симметрии может быть выбрано либо неравенство бесконечности температуры на оси цилиндра, либо отсутствие теплового потока на оси цилиндра, т.е.
Общее решение дифференциального уравнения есть
Граничное условие на оси цилиндра даёт C1 = 0, а граничное условие на поверхности цилиндра записывается в виде
откуда находится C2 , которая, будучи подставленной в , даёт температурное поле для решаемой задачи
При однородном тепловыделении, т.е. когда 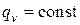
есть так называемый критерий (число) Био для цилиндра.
Температуры на оси цилиндра и на его поверхности равны соответственно
Для корректного изображения радиального распределения температур составим отношение
из которого следует, что при малых значениях критерия Био (большая теплопроводность материала стержня и/или малый коэффициент теплоотдачи) температура в стержне в радиальном направлении меняется незначительно по сравнению с перепадом температур в пограничном слое вблизи поверхности стержня. И напротив, при больших значениях критерия Био перепад температур в стержне велик по сравнению с перепадом температур в пограничном слое. Эти два варианта представлены на рис. III.7.
8.Стационарная теплопроводность вдоль прямого стержня конечной длины в одномерном приближении при однородных граничных условиях III рода на наружной поверхности
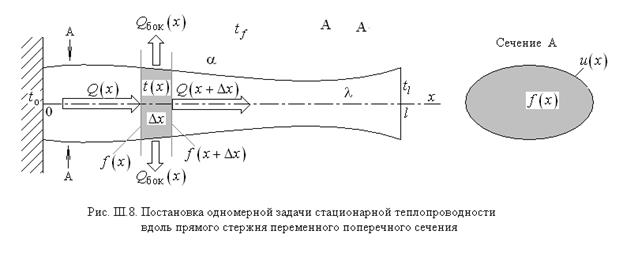
Задача вычисления теплового потока вдоль стержня (определение стержня дано в сноске 3 на стр. 15) представляет практический интерес в проблеме охлаждения теплонапряжённых поверхностей с применением оребрения, охлаждения радиоэлектронного оборудования и т. п.
Пусть прямой стержень конечной длины и переменного поперечного сечения (см. рис. III.8) находится в условиях, когда один из его торцов (на рисунке левый) поддерживается при постоянной по сечению «заделки» температуре 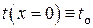
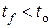
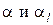
Дифференциальное уравнение теплопроводности в данном случае записывается в виде
с граничными условиями, которые в общем виде представляются в данной задаче в виде
Ясно, что точное решение этой задачи, даже если это возможно, не представляет большого практического интереса, так как обычно интересуются распределением температуры вдоль стержня, а не в его поперечных сечениях. Тем более можно с достаточной степенью точности пренебречь неравномерностью температурного поля в поперечных сечениях, если теплопроводность материала стержня достаточно велика (см. рис. III.7). Тогда температуру можно считать зависящей только от одной координаты x, направленной вдоль продольной оси стержня. Второе граничное условие в при этом становится неопределённым
Эта неопределённость снимается перепостановкой задачи – . Для этого выделим элемент длины стержня 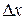
Используя определение плотности теплового потока и гипотезу Ньютона-Рихмана, последнее выражение записывается в развёрнутом виде
Здесь 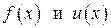
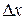
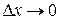
Далее, используя закон Био-Фурье для одномерного случая, приходим к дифференциальному уравнению теплопроводности при перечисленных выше допущениях
В качестве граничных условий для этого обыкновенного квазилинейного неоднородного дифференциального уравнения второго порядка положим
где l – длина стержня; 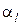
Введя относительную температуру согласно определению
задачу – запишем в более компактной форме (аргумент x опускаем)
В качестве приложений рассмотрим некоторые одномерные задачи стационарной теплопроводности вдоль стержней и рёбер.
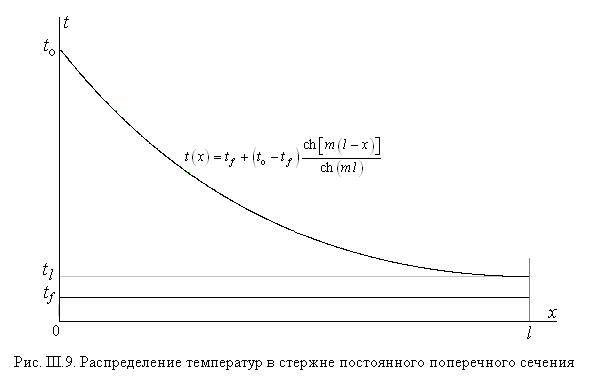
А. Теплопроводность вдоль стержня постоянного поперечного сечения и формы, т. е. 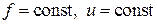
Общее решение дифференциального уравнения есть
Граничные условия в приводят к системе двух линейных алгебраических уравнений для вычисления произвольных постоянных 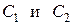
Решение этой системы даёт следующее распределение температур по длине стержня
С использованием определения гиперболических функций
решение записывается в более компактном виде
В большинстве практических случаев комплекс 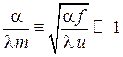
Этот случай предполагает отсутствие теплового потока с торцевой поверхности стержня – второе условие в . Заметим, что уравнение носит название цепной линии.
Качественная зависимость 
Температура на свободном конце стержня
Полный стационарный тепловой поток через стержень может быть вычислен двумя способами: либо с использованием закона Био-Фурье (дифференцированием аксиального распределения температур ), либо интегрированием линейной плотности теплового потока с боковой поверхности, т. е.
Параллельные вычисления приводят к следующему результату
Из этого выражения следует, что тепловой поток через стержень пропорционален, кроме прочих величин, коэффициенту теплопроводности материала стержня 
носит название эффективности работы ребра (стержня).
Вычислим далее тепловой поток, который бы снимался с пятна контакта стержня с поверхностью заделки в отсутствие стержня
Разделив на с учётом , получим
где 
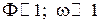
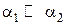
откуда легко видеть, что повышение меньшего коэффициента теплоотдачи 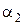
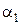
Таким образом, оребрение поверхности видоизменяет выражение для коэффициента теплоотдачи
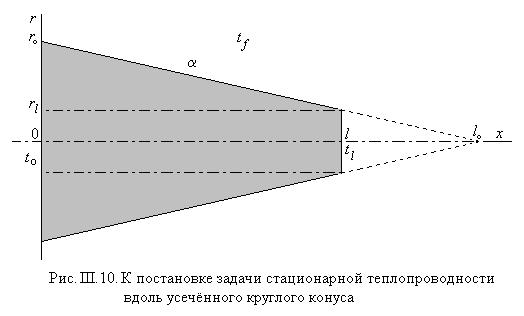
Б. Теплопроводность вдоль стержня в форме прямого круглого усечённого конуса
В этом случае (см. рис. III.10)
Имеем
Задача принимает тогда вид
Введя безразмерную независимую переменную 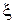
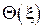
запишем задачу теплопроводности в безразмерном виде
где введены обозначения
Заменой независимой переменной
задача приводится к виду
Общее решение дифференциального уравнения в выражается через функции Бесселя (цилиндрические функции) первого и второго рода первого порядка от мнимого аргумента (см. справочники: 1)Рыжик, Градштейн; 2) Камке)
Используя формулы дифференцирования и рекуррентные соотношения для функций Бесселя (см. справочник Бронштейн, Семендяев), находим
Используя эти результаты и граничные условия в , получаем алгебраическую систему уравнений для нахождения произвольных постоянных
где 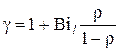
Здесь использованы рекуррентные соотношения для бесселевых функций мнимого аргумента (см. справочник Бронштейн, Семендяев)
В частном случае, когда можно пренебречь тепловым потоком с торца конического стержня ( 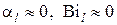
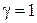
откуда для данного случая находим распределение температур по длине стержня конечной длины конической конфигурации
В предельных случаях неусечённого конуса 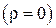
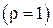
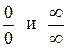
и применяя правило Лопиталя, после громоздких вычислений получаем
Заметим, что второе выражение в полностью совпадает с полученным ранее выражением для стержня с постоянным сечением.
Тепловой поток через стержень вычисляется согласно , при этом для сечения 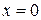
или с заменой переменной 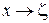
Используя и , находим производную 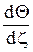
В предельных случаях 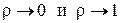
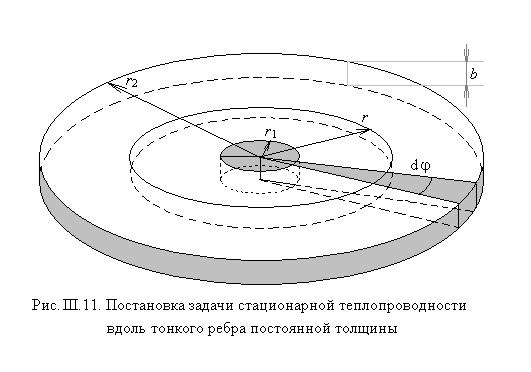
В. Теплопроводность вдоль круглого ребра постоянной толщины
Оребрение поверхностей для увеличения теплосъёма с теплонапряжённых поверхностей весьма распространено в автомобильной промышленности, в химической технологии, в энергетике и т. д. И чаще всего охлаждающие рёбра имеют форму плоских дисков (см. рис. III.11).
В этом случае площадь поперечного сечения 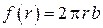
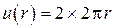
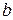
Решение этого уравнения, удовлетворяющее граничным условиям, есть
Относительная температура внешнего среза ребра будет тогда
Тепловой поток через цилиндрическое ребро постоянной толщины
Г. Теплопроводность вдоль круглого ребра постоянной площади кольцевого поперечного сечения
В случае круглого ребра постоянной площади кольцевого поперечного сечения (см. рис. 14) площадь кольцевого сечения равна 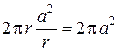
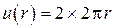
Общее решение этого уравнения представляется комбинацией модифицированных функций Бесселя мнимого аргумента порядка 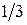
Используя известные рекуррентные формулы и формулы дифференцирования модифицированных бесселевых функций
и граничные условия в постановке задачи , после несложных, но трудоёмких алгебраических преобразований получаем
Из этих соотношений находим относительную температуру на наружном радиусе ребра
и тепловой поток вдоль ребра
В заключение приведём полезные для численного счёта представления в виде рядов модифицированных функций Бесселя нецелого порядка
Дата добавления: 2015-12-17 ; просмотров: 6215 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
💡 Видео
Дифракция электронов на поликристаллеСкачать

Электрохимические методы анализа. Часть 1.Скачать

Теория отталкивания электронных пар. Метод Гиллеспи. 1 часть. 10 класс.Скачать
лекция 412 Элементы зонной теории проводимостиСкачать

Метод узловых потенциалов. Решение задачи в программе mathcadСкачать

Современные электротехнологии в металлургии. Методы их разработки и исследованияСкачать

Основы электротехники. 01. ВведениеСкачать

Электробезопасность. Выпуск 1: Основы электротехникиСкачать

Проведение игольчатой электромиографии (ЭМГ)Скачать

Электростатическая индукцияСкачать

Урок 267. Компенсационные методы измерения ЭДС и сопротивленияСкачать

Теория отталкивания электронных пар. 10 класс.Скачать

Аналогово-цифровое преобразование ЛЕКЦИЯСкачать