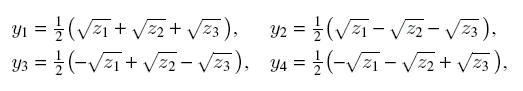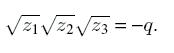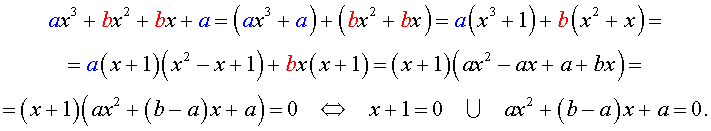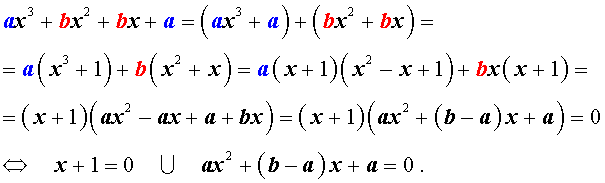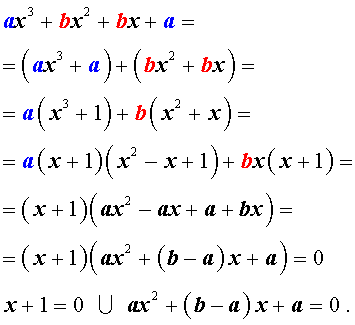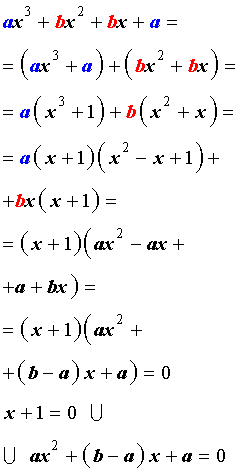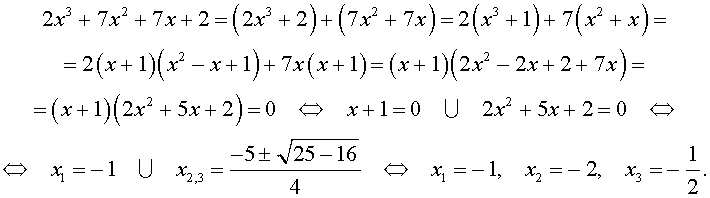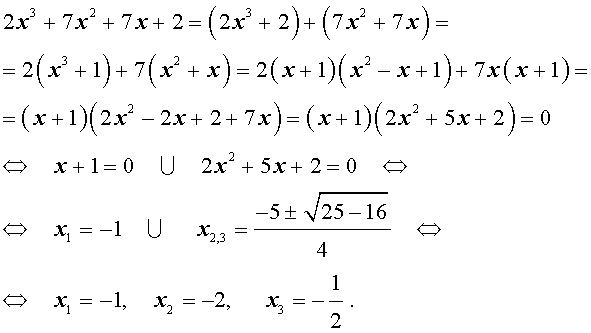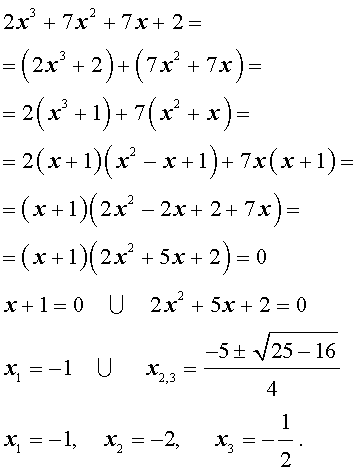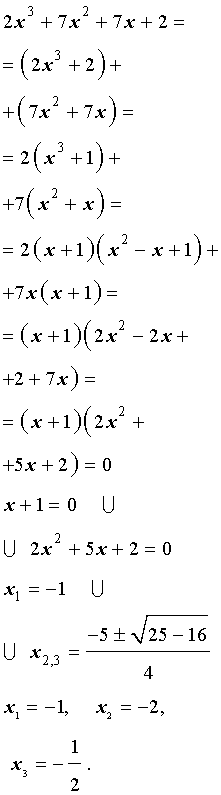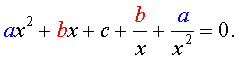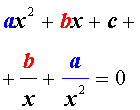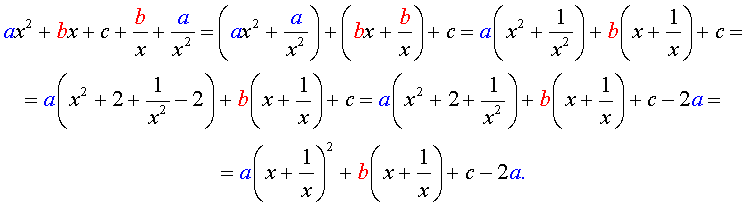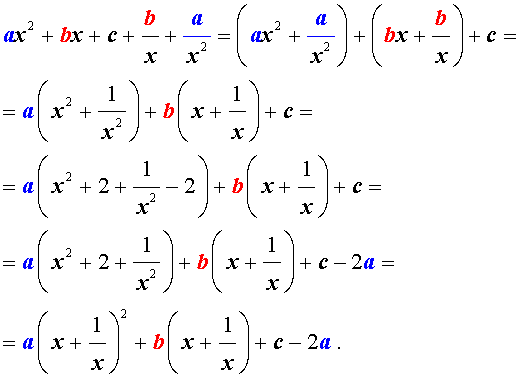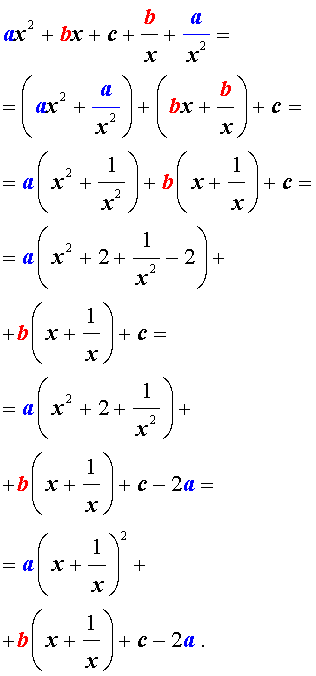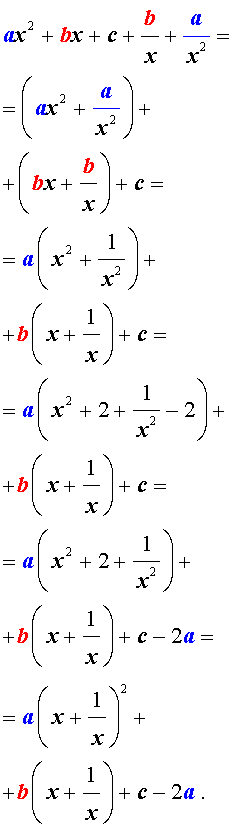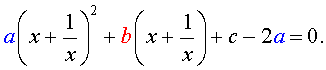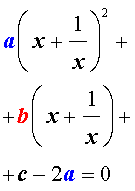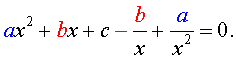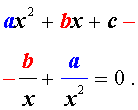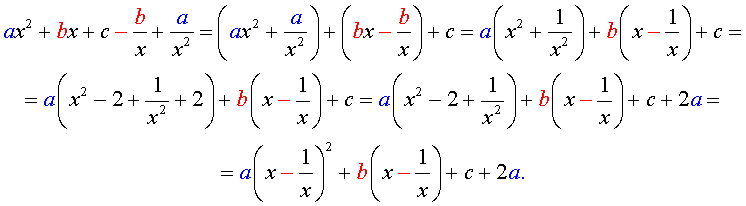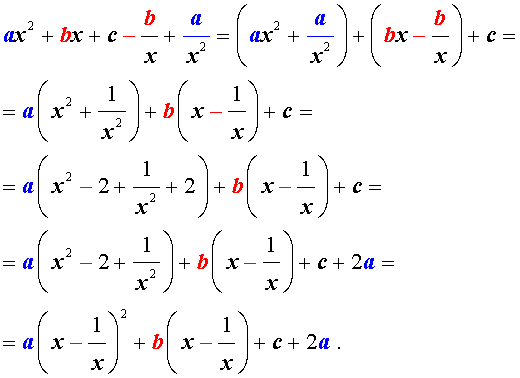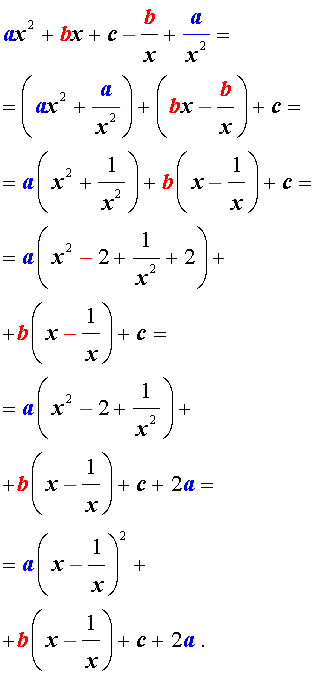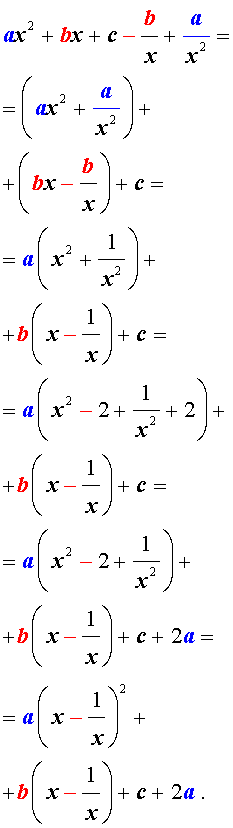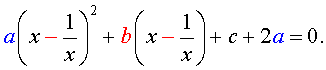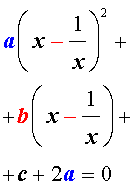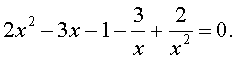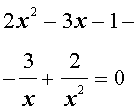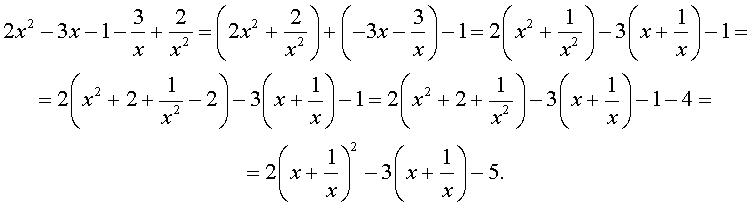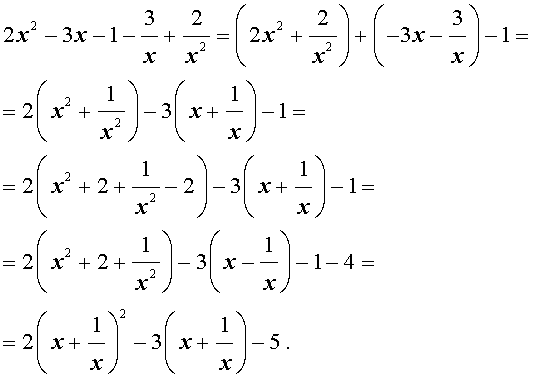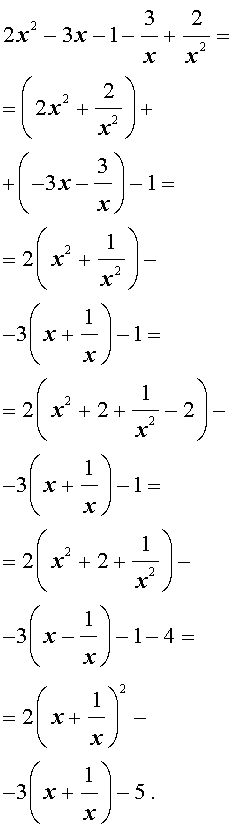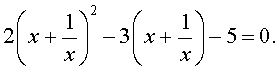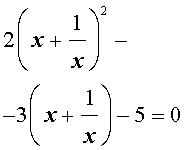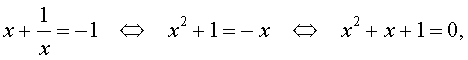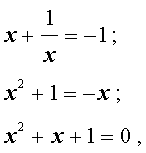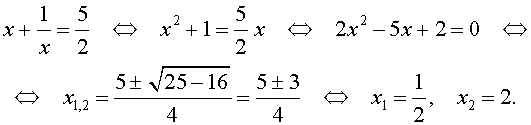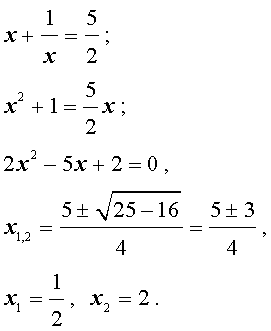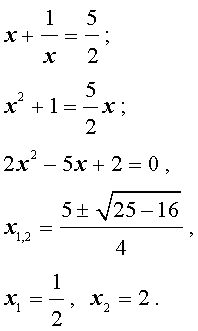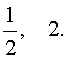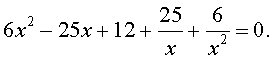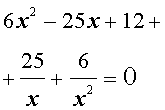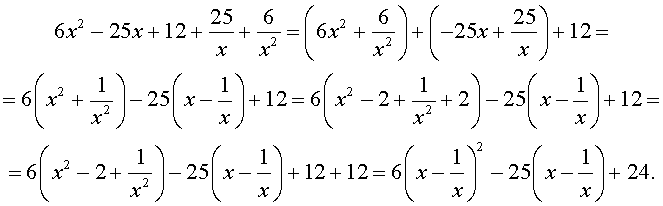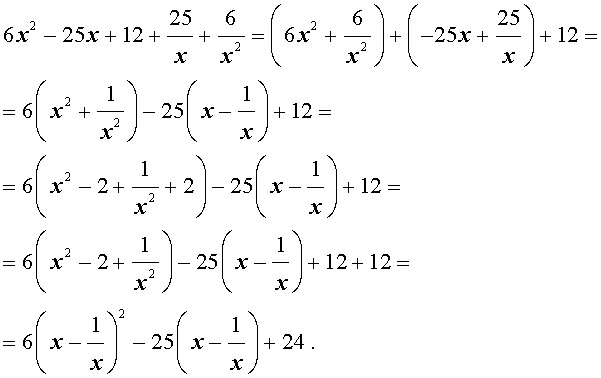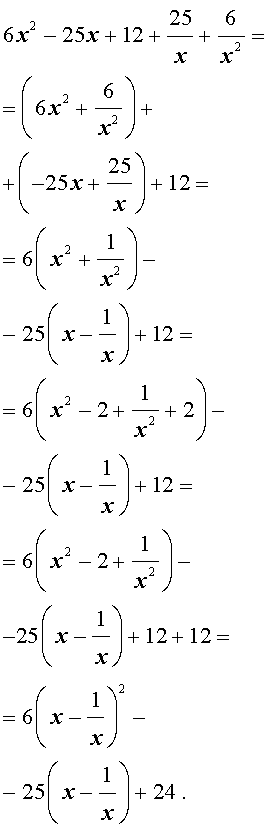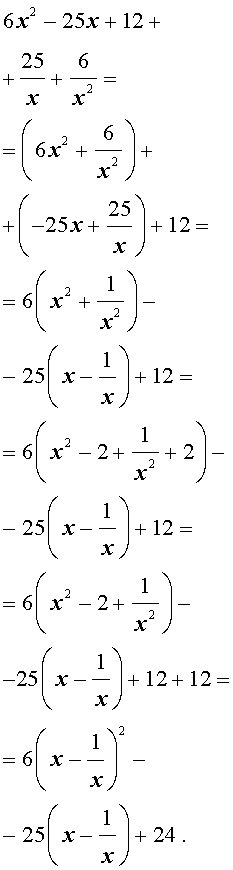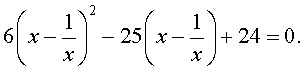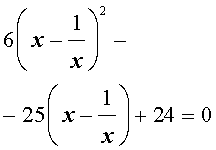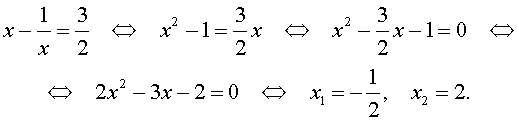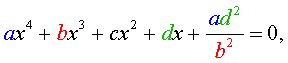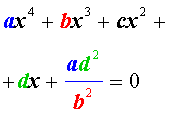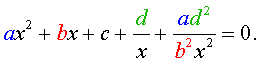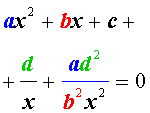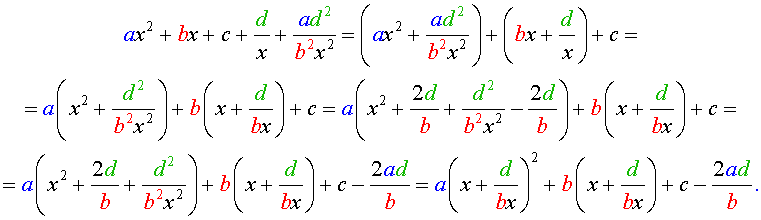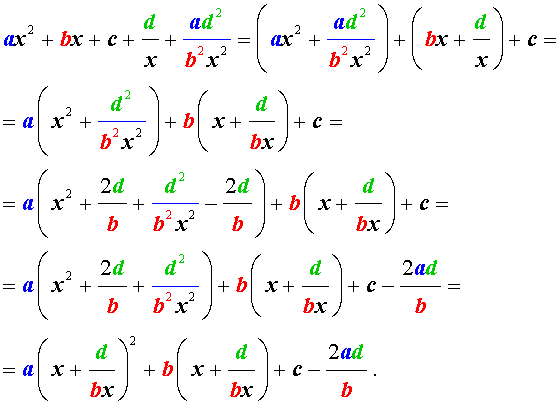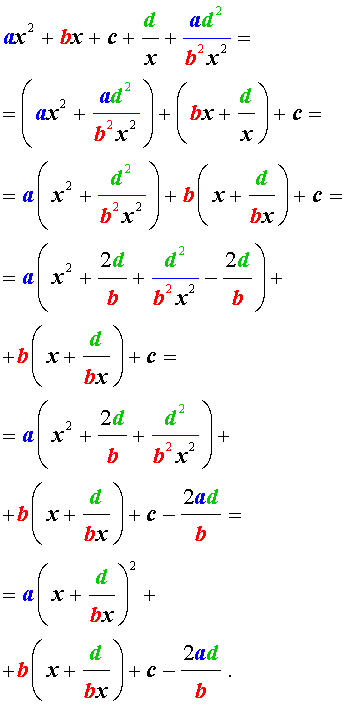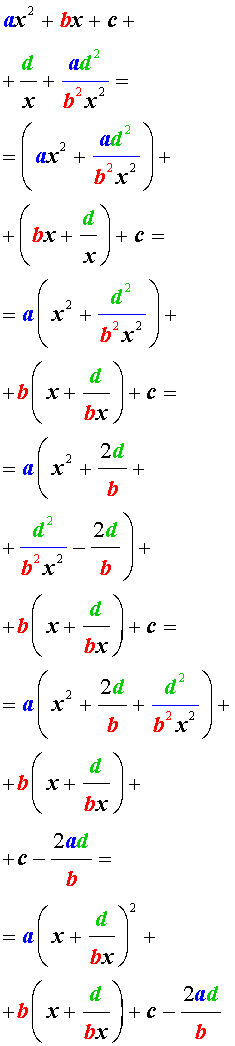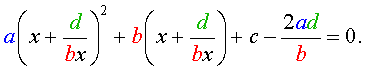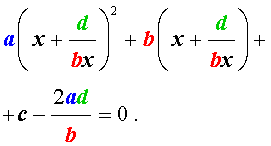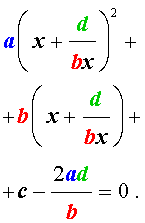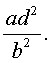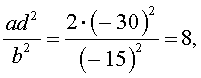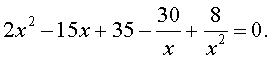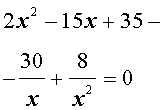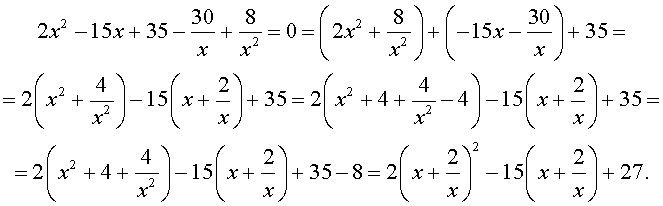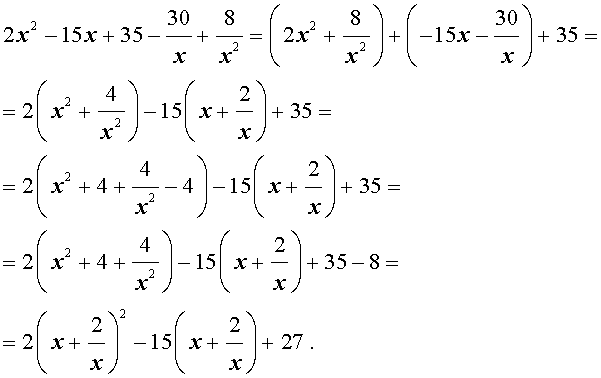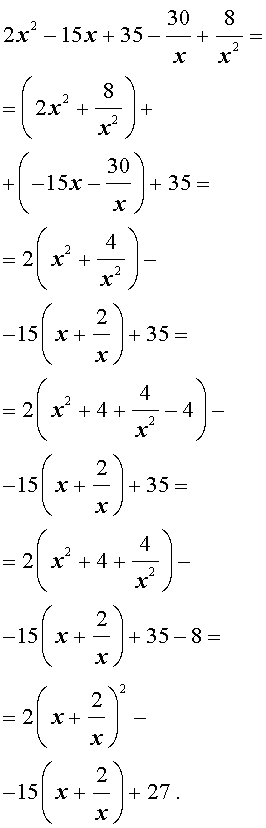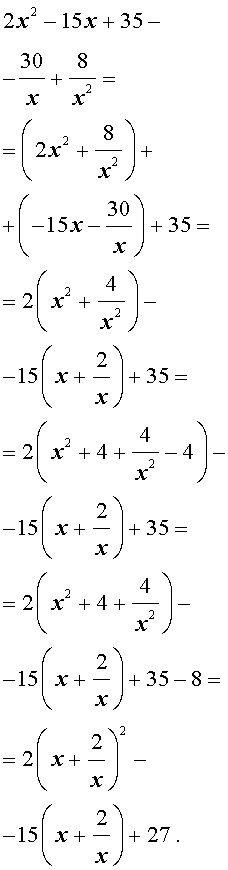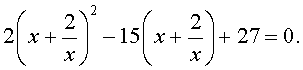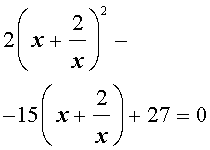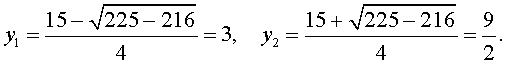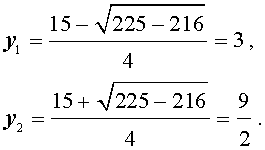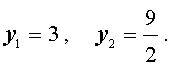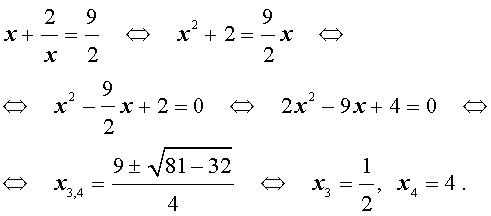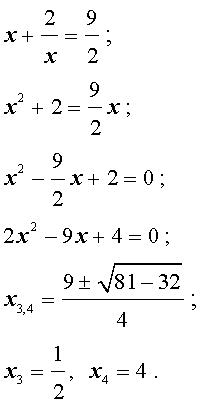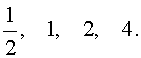Для уравнений четвертой степени применимы все те общие схемы решения уравнений высших степеней, что мы разбирали в предыдущем материале. Однако существует ряд нюансов в решении двучленных, биквадратных и возвратных уравнений, на которых мы хотели бы остановиться подробнее.
Также в статье мы разберем искусственный метод разложения многочлена на множители, решение в радикалах и метод Феррари, который используется для того, чтобы свести решение уравнения четвертой степени к кубическому уравнению.
- Решение двучленного уравнения четвертой степени
- Решение возвратного уравнения четвертой степени
- Решение биквадратного уравнения
- Решение уравнений четвертой степени с рациональными корнями
- Решение уравнений четвертой степени по методу Феррари
- Метод декарта эйлера решения уравнений 4 степени
- Уравнения, сводящиеся к квадратным уравнениям: возвратные (симметричные) уравнения
- Возвратные (симметричные) уравнения 3-ей степени
- Возвратные (симметричные) уравнения 4-ой степени
- Обобщенные возвратные уравнения 4-ой степени
- 🎥 Видео
Видео:Метод Декарта-Эйлера (решение уравнения четвертой степени)Скачать

Решение двучленного уравнения четвертой степени
Это простейший тип уравнений четвертой степени. Запись уравнения имеет вид A x 4 + B = 0 .
Для решения этого типа уравнений применяются формулы сокращенного умножения:
A x 4 + B = 0 x 4 + B A = 0 x 4 + 2 B A x 2 + B A — 2 B A x 2 = 0 x 2 + B A 2 — 2 B A x 2 = 0 x 2 — 2 B A 4 x + B A x 2 + 2 B A 4 x + B A = 0
Остается лишь найти корни квадратных трехчленов.
Решить уравнение четвертой степени 4 x 4 + 1 = 0 .
Решение
Для начала проведем разложение многочлена 4 x 4 + 1 на множители:
4 x 4 + 1 = 4 x 4 + 4 x 2 + 1 = ( 2 x 2 + 1 ) 2 — 4 x 2 = 2 x 2 — 2 x + 1 ( 2 x 2 + 2 x + 1 )
Теперь найдем корни квадратных трехчленов.
2 x 2 — 2 x + 1 = 0 D = ( — 2 ) 2 — 4 · 2 · 1 = — 4 x 1 = 2 + D 2 · 2 = 1 2 + i x 2 = 2 — D 2 · 2 = 1 2 — i
2 x 2 + 2 x + 1 = 0 D = 2 2 — 4 · 2 · 1 = — 4 x 3 = — 2 + D 2 · 2 = — 1 2 + i x 4 = — 2 — D 2 · 2 = — 1 2 — i
Мы получили четыре комплексных корня.
Ответ: x = 1 2 ± i и x = — 1 2 ± i .
Видео:Решение уравнений четвертой степени. Идея метода ФеррариСкачать

Решение возвратного уравнения четвертой степени
Возвратные уравнения четвертого порядка имеют вид A x 4 + B x 3 + C x 2 + B x + A = 0
х = 0 не является корнем этого уравнения: A · 0 4 + B · 0 3 + C · 0 2 + B · 0 + A = A ≠ 0 . Поэтому на x 2 можно смело разделить обе части этого уравнения:
A x 4 + B x 3 + C x 2 + B x + A = 0 A x 2 + B x + C + B x + A x 2 = 0 A x 2 + A x 2 + B x + B x + C = 0 A x 2 + 1 x 2 + B x + 1 x + C = 0
Проведем замену переменных x + 1 x = y ⇒ x + 1 x 2 = y 2 ⇒ x 2 + 1 x 2 = y 2 — 2 :
A x 2 + 1 x 2 + B x + 1 x + C = 0 A ( y 2 — 2 ) + B y + C = 0 A y 2 + B y + C — 2 A = 0
Так мы проведи сведение возвратного уравнения четвертой степени к квадратному уравнению.
Найти все комплексные корни уравнения 2 x 4 + 2 3 + 2 x 3 + 4 + 6 x 2 + 2 3 + 2 x + 2 = 0 .
Решение
Симметрия коэффициентов подсказывает нам, что мы имеем дело с возвратным уравнением четвертой степени. Проведем деление обеих частей на x 2 :
2 x 2 + 2 3 + 2 x + 4 + 6 + 2 3 + 2 x + 2 x 2 = 0
2 x 2 + 2 x 2 + 2 3 + 2 x + 2 3 + 2 x + 4 + 6 + = 0 2 x 2 + 1 x 2 + 2 3 + 2 x + 1 x + 4 + 6 = 0
Проведем замену переменной x + 1 x = y ⇒ x + 1 x 2 = y 2 ⇒ x 2 + 1 x 2 = y 2 — 2
2 x 2 + 1 x 2 + 2 3 + 2 x + 1 x + 4 + 6 = 0 2 y 2 — 2 + 2 3 + 2 y + 4 + 6 = 0 2 y 2 + 2 3 + 2 y + 6 = 0
Решим полученное квадратное уравнение:
D = 2 3 + 2 2 — 4 · 2 · 6 = 12 + 4 6 + 2 — 8 6 = = 12 — 4 6 + 2 = 2 3 — 2 2 y 1 = — 2 3 — 2 + D 2 · 2 = — 2 3 — 2 + 2 3 — 2 4 = — 2 2 y 2 = — 2 3 — 2 — D 2 · 2 = — 2 3 — 2 — 2 3 + 2 4 = — 3
Вернемся к замене: x + 1 x = — 2 2 , x + 1 x = — 3 .
Решим первое уравнение:
x + 1 x = — 2 2 ⇒ 2 x 2 + 2 x + 2 = 0 D = 2 2 — 4 · 2 · 2 = — 14 x 1 = — 2 — D 2 · 2 = — 2 4 + i · 14 4 x 2 = — 2 — D 2 · 2 = — 2 4 — i · 14 4
Решим второе уравнение:
x + 1 x = — 3 ⇒ x 2 + 3 x + 1 = 0 D = 3 2 — 4 · 1 · 1 = — 1 x 3 = — 3 + D 2 = — 3 2 + i · 1 2 x 4 = — 3 — D 2 = — 3 2 — i · 1 2
Ответ: x = — 2 4 ± i · 14 4 и x = — 3 2 ± i · 1 2 .
Видео:Уравнение четвертой степениСкачать

Решение биквадратного уравнения
Биквадратные уравнения четвертой степени имеют вид A x 4 + B x 2 + C = 0 . Мы можем свести такое уравнение к квадратному A y 2 + B y + C = 0 путем замены y = x 2 . Это стандартный прием.
Решить биквадратное уравнение 2 x 4 + 5 x 2 — 3 = 0 .
Решение
Выполним замену переменной y = x 2 , что позволит нам свести исходное уравнение к квадратному:
2 y 2 + 5 y — 3 = 0 D = 5 2 — 4 · 2 · ( — 3 ) = 49 y 1 = — 5 + D 2 · 2 = — 5 + 7 4 = 1 2 y 2 = — 5 — D 2 · 2 = — 5 — 7 4 = — 3
Следовательно, x 2 = 1 2 или x 2 = — 3 .
Первое равенство позволяет нам получить корень x = ± 1 2 . Второе равенство не имеет действительных корней, зато имеет комплексно сопряженных корней x = ± i · 3 .
Ответ: x = ± 1 2 и x = ± i · 3 .
Найти все комплексные корни биквадратного уравнения 16 x 4 + 145 x 2 + 9 = 0 .
Решение
Используем метод замены y = x 2 для того, чтобы свести исходное биквадратное уравнение к квадратному:
16 y 2 + 145 y + 9 = 0 D = 145 2 — 4 · 16 · 9 = 20449 y 1 = — 145 + D 2 · 16 = — 145 + 143 32 = — 1 16 y 2 = — 145 — D 2 · 16 = — 145 — 143 32 = — 9
Поэтому, в силу замены переменной, x 2 = — 1 16 или x 2 = — 9 .
Ответ: x 1 , 2 = ± 1 4 · i , x 3 , 4 = ± 3 · i .
Видео:9 класс. Алгебра. Решение уравнений четвертой степени. Возвратные уравнения.Скачать

Решение уравнений четвертой степени с рациональными корнями
Алгоритм нахождения рациональных корней уравнения четвертой степени приведен в материале «Решение уравнений высших степеней».
Видео:Как решать уравнения четвёртой степени. Формула Феррари | #БотайСоМной #026 | Борис ТрушинСкачать

Решение уравнений четвертой степени по методу Феррари
Уравнения четвертой степени вида x 4 + A x 3 + B x 2 + C x + D = 0 в общем случае можно решить с применением метода Феррари. Для этого необходимо найти y 0 . Это любой из корней кубического уравнения y 3 — B y 2 + A C — 4 D y — A 2 D + 4 B D — C 2 = 0 . После этого необходимо решить два квадратных уравнения x 2 + A 2 x + y 0 2 + A 2 4 — B + y 0 x 2 + A 2 y 0 — C x + y 0 2 4 — D = 0 , у которых подкоренное выражение является полным квадратом.
Корни, полученные в ходе вычислений, будут корнями исходного уравнения четвертой степени.
Найти корни уравнения x 4 + 3 x 3 + 3 x 2 — x — 6 = 0 .
Решение
Имеем А = 3 , В = 3 , С = — 1 , D = — 6 . Применим метод Феррари для решения данного уравнения.
Составим и решим кубическое уравнение:
y 3 — B y 2 + A C — 4 D y — A 2 D + 4 B D — C 2 = 0 y 3 — 3 y 2 + 21 y — 19 = 0
Одним из корней кубического уравнения будет y 0 = 1 , так как 1 3 — 3 · 1 2 + 21 · 1 — 19 = 0 .
Запишем два квадратных уравнения:
x 2 + A 2 x + y 0 2 ± A 2 4 — B + y 0 x 2 + A 2 y 0 — C x + y 0 2 4 — D = 0 x 2 + 3 2 x + 1 2 ± 1 4 x 2 + 5 2 x + 25 4 = 0 x 2 + 3 2 x + 1 2 ± 1 2 x + 5 2 2 = 0
x 2 + 3 2 x + 1 2 + 1 2 x + 5 2 = 0 или x 2 + 3 2 x + 1 2 — 1 2 x — 5 2 = 0
x 2 + 2 x + 3 = 0 или x 2 + x — 2 = 0
Корнями первого уравнения будут x = — 1 ± i · 2 , корнями второго х = 1 и х = — 2 .
Ответ: x 1 , 2 = — 1 ± i 2 , x 3 = 1 , x 4 = — 2 .
Видео:Как решать уравнения 4 степени Решите уравнение четвертой степени Разложить на множители Безу столбиСкачать

Метод декарта эйлера решения уравнений 4 степени
Уравнение четвертой степени общего вида
ax 4 + bx 3 + cx 2 + dx + e = 0. — Уравнение четвертой степени общего вида.
1. Сокращение до неполного уравнения
Уравнение четвертой степени в общем сокращается до неполного уравнения
y 4 + py 2 + qy + r = 0
при помощи замены переменных
2. Решение Декарта — Эйлера
Корни неполного уравнения четвертой степени определяются формулами:
где z1, z2, z3 это корни кубического уравнения
z 3 + 2pz 2 + (p 2 — 4r) — q 2 = 0,
которое называется резольвентой исходного уравнения. Знаки корней в ней выбираются таким образом, чтобы выполнялось равенство:
Корни неполного исходного уравнения определяются корнями кубической резольвенты согласно таблице:
Связь между корнями неполного уравнения четвертой степени и корнями резольвенты
| Кубическая резольвента | Уравнение четвертой степени |
| Все корни действительные и положительные (*) | Четыре действительных корня |
| Все корни действительные, они положительный и два отрицательных (*) | Две пары комплексно сопряженных корней |
| Один корень положительный, два комплексно-сопряженные | Два действительных и два комплексно-сопряженных корня |
(*) — по теореме Виета, произведение корней z1, z2, z3 = q 2
3. Решение Феррари
Предположим, z0 — один из корней вспомогательного кубического уравнения.
z 3 + 2pz 2 + (p 2 — 4r) — q 2 = 0,
Тогда четрые корня неполного уравнения четвертой степени находятся при помощи решения двух квадратных уравнений
Видео:(Часть 2) Уравнение 4-й степени (метод 1)Скачать

Уравнения, сводящиеся к квадратным уравнениям:
возвратные (симметричные) уравнения
Существует ряд уравнений, которые удается решить при помощи сведения их к квадратным уравнениям.
К таким уравнениям, в частности, относятся уравнения следующих типов:
 | Трёхчленные уравнения |
 | Уравнения 4-ой степени, левая часть которых равна произведению четырёх последовательных членов арифметической прогрессии |
 | Возвратные (симметричные) уравнения 3-ей степени |
 | Возвратные (симметричные) уравнения 4-ой степени |
 | Обобщенные возвратные уравнения 4-ой степени |
Замечание . Уравнения, носящие название «Биквадратные уравнения» , относятся к типу «Трехчленные уравнения» .
Видео:Решение уравнений 4 степениСкачать

Возвратные (симметричные) уравнения 3-ей степени
Возвратным уравнением 3-ей степени называют уравнение вида
| a x 3 + b x 2 + b x + a = 0, | (1) |
где a , b – заданные числа.
Решение уравнения (1) осуществляется при помощи разложения левой части уравнения (1) на множители:
Для завершения решения уравнения (1) остаётся лишь решить квадратное уравнение
Пример 1 . Решить уравнение
| 2x 3 + 7x 2 + 7x + 2 = 0. | (2) |
Решение . Разложим левую часть уравнения (2) на множители:
Ответ :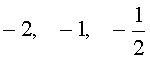
Видео:Как решать уравнения высших степеней, очень лёгкий способ!!!Скачать

Возвратные (симметричные) уравнения 4-ой степени
Возвратными (симметричными) уравнениями 4-ой степени называют уравнения вида
| a x 4 + b x 3 + cx 2 + + b x + a = 0, | (3) |
а также уравнения вида
| a x 4 + b x 3 + cx 2 – – b x + a = 0, | (4) |
Для того, чтобы решить возвратное уравнение (3), разделим его на x 2 . В результате получится уравнение
Преобразуем левую часть уравнения (5):
В результате этого преобразования уравнение (5) принимает вид
Если теперь обозначить
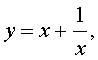 | (7) |
то уравнение (6) станет квадратным уравнением:
| a y 2 + b y + c – 2 a = 0. | (8) |
Найдем корни уравнения (8), а после этого, подставив каждый из найденных корней в равенство (7), решим полученное уравнение относительно x .
Описание метода решения уравнений вида (3) завершено.
Для того, чтобы решить возвратное уравнение (4), разделим его на x 2 . В результате получится уравнение
Преобразуем левую часть уравнения (9):
В результате этого преобразования уравнение (9) принимает вид
Если теперь обозначить
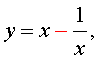 | (11) |
то уравнение (10) станет квадратным уравнением:
| a y 2 + b y + c + 2 a = 0. | (12) |
Найдем корни уравнения (13), а после этого, подставив каждый из найденных корней в равенство (11), решим полученное уравнение относительно x .
Описание метода решения уравнений вида (4) завершено.
Пример 2 . Решить уравнение
| 2x 4 – 3x 3 – x 2 – – 3x + 2 = 0. | (13) |
Решение . Уравнение (13) является возвратным и относится к виду (3). Разделим его на x 2 . В результате получится уравнение
Преобразуем левую часть уравнения (14):
В результате этого преобразования уравнение (14) принимает вид
Если теперь обозначить
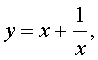 | (16) |
то уравнение (15) станет квадратным уравнением:
| 2y 2 – 3y – 5 = 0. | (17) |
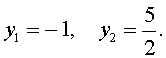 | (18) |
В первом случае из равенства (16) получаем уравнение:
которое решений не имеет.
Во втором случае из равенства (16) получаем:
Ответ :
Пример 3 . Решить уравнение
| 6x 4 – 25x 3 + 12x 2 + + 25x + 6 = 0. | (19) |
Решение . Уравнение (19) является возвратным и относится к виду (4). Разделим его на x 2 . В результате получится уравнение
Преобразуем левую часть уравнения (20):
В результате этого преобразования уравнение (20) принимает вид
Если теперь обозначить
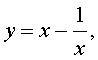 | (22) |
то уравнение (21) станет квадратным уравнением:
| 6y 2 – 25y + 24 = 0. | (23) |
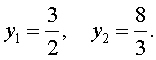 | (24) |
В первом случае из равенства (22) получаем:
Во втором случае из равенства (22) получаем:
Ответ :
Видео:Решаем быстро и красиво ★ Уравнение четвертой степени ★ x^4+8x-7=0Скачать

Обобщенные возвратные уравнения 4-ой степени
Обобщенным возвратным уравнением 4-ой степени назовём уравнение вида
где a , b , c, d – заданные числа.
Для того, чтобы решить уравнение (25), разделим его на x 2 . В результате получится уравнение
Преобразуем левую часть уравнения (26):
В результате этого преобразования уравнение (26) принимает вид
Если теперь обозначить
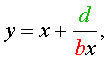 | (28) |
то уравнение (27) станет квадратным уравнением:
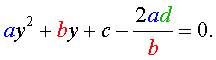 | (29) |
Найдем корни уравнения (29), а после этого, подставив каждый из найденных корней в равенство (28), решим полученное уравнение относительно x .
Описание метода решения уравнений вида (25) завершено.
Пример 4 . Решить уравнение
| 2x 4 – 15x 3 + 35x 2 – – 30 x + 8 = 0. | (30) |
Решение . Введем для коэффициентов уравнения (30) следующие обозначения
и найдем значение выражения
то уравнение (30) является обобщенным возвратным уравнением 4-ой степени. В соответствии с изложенным выше, разделим его на x 2 . В результате получится уравнение
Преобразуем левую часть уравнения (31):
В результате этого преобразования уравнение (31) принимает вид
Если теперь обозначить
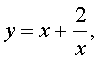 | (33) |
то уравнение (32) станет квадратным уравнением:
| 2y 2 – 15y + 27 = 0. | (34) |
В первом случае из равенства (33) получаем:
Во втором случае из равенства (33) получаем:
Ответ :
🎥 Видео
Как решать возвратные уравнения?Скачать

УДИВИТЕЛЬНЫЙ способ решения уравнения 4-ой степениСкачать

Остаток от деления 14^245 на 90 | Теорема Эйлера | Теория чисел | КАК РЕШАТЬ?Скачать

Симметрические уравнения третьей и четвертой степениСкачать

Математика | Кубические уравнения по методу СталлонеСкачать

УДИВИТЕЛЬНЫЙ способ решения уравнения ★ Вы такого не видели! ★ Уравнение четвертой степениСкачать

Задача Декарта ➜ Решите уравнение: x⁴-4x³-19x²+106x-120=0Скачать

(Часть 1) Уравнение 4-й степени (метод 1)Скачать

Решение уравнения четвертой степени в общем виде!Скачать

Уравнение 4-й степени. Метод ФеррариСкачать