Метод даламбера для дифференциальных уравнений

Видео:Принцип ДаламбераСкачать

Лекция 6. Метод Даламбера

В этой лекции решение задачи Коши для волнового уравнения

Шаг 1. Заменим переменные (x, t) новыми переменными (ξ,η), в которых волновое уравнение примет другой вид: Такая замена выполняется по формулам

После подстановки этих производных в волновое уравнение, получим:

что и требовалось доказать.

Шаг 2. Преобразованное уравнение легко решается двумя последовательными интегрированиями (сначала по переменной η , а затем по ξ):

где C₁(η) – произвольная функция от η. Так как C(ξ) – произвольная функция, то и – также произвольная функция.

Окончательно, общее решение U(ξ,η) имеет вид

Шаг 3. Для нахождения общего решения первоначального уравнения подставим в (25) вместо ξ и η выражения (24):

Шаг 4. Определим функции C₁ и C₂, используя начальные условия из (23). После подстановки первого условия получим

Найдем производную функции U в (26) по переменной t и подставим второе условие:

В результате будем иметь систему уравнений

Если проинтегрировать второе уравнение системы (27) по x в пределах от x_o до х , то получим следующую систему:

При сложении этих уравнений получим

Если из первого уравнения системы вычесть второе уравнение, то будем иметь

Подставим теперь полученные функции в общее решение (26):

Поменяем местами пределы интегрирования во втором интеграле, стоящем в скобках в (28). В результате получим решение исходной задачи Коши

Формула (29) называется формулой Даламбера.

Далее мы исследуем решение, определяемое по формуле Даламбера.

Пространственно-временная интерпретация формулы Даламбера

При исследовании формулы Даламбера будем исходить из физического смысла волнового уравнения. Рассмотрим уравнение свободных колебаний бесконечной струны

и начальные условия

Такая задача Коши с помощью замены независимой переменной сводится к задаче (23):

Решение преобразованной задачи имеет вид (см. формулу Даламбера (29):

Если теперь в эту формулу вместо τ подставить at, то получится решение исходной задачи

Прежде, чем перейти к физической интерпретации этой формулы, сделаем следующее замечание.

Замечание. Рассмотрим в отдельности функции C₁(x-at) и C₂(x-at), входящие в общее решение (26) (коэффициент а в них появился потому, что нас сейчас интересует более общее уравнение (30)). Начнем с функции C₁(x-at) и построим графики этой функции при возрастающих значениях t: t=t_o, t=t₁, t=t₂ и т.д. (см. рис. 8).

Если по очереди проецировать эти картинки на экран (как в мультфильмах), то они «побегут» вправо. Процесс передвижения отклонения по струне называется волной. При этом коэффициент а является скоростью распространения волны. В самом деле, предположим, что параллельно оси х движется наблюдатель со скоростью а. Пусть в некоторый момент t_o он находился в точке x_o. Тогда за промежуток наблюдатель сместится вправо на величину и окажется в точке Если в точке x_o наблюдатель видел отклонение струны на величину то в момент t величина отклонения – будет точно такой же! То есть наблюдатель будет видеть форму струны не изменяющейся.

Вторая функция C₂(x-at) тоже представляет собой волну, но только она будет распространяться со скоростью а влево. Часто функции C₁(x-at) и C₂(x-at) называют, соответственно, прямой и обратной волной. Таким образом, общее решение U(x,t) (формула (26)) волнового уравнения является суперпозицией прямой и обратной волны.

Теперь дадим интерпретацию формулы Даламбера для двух частных случаев.

СЛУЧАЙ 1. Предположим, что начальное отклонение отлично от нуля, а начальная скорость равна нулю. Это означает, что начальные условия имеют вид

При таких начальных условиях получается решение задачи Коши, которое называется волной отклонения. Уравнение волны отклонения определяется формулой Даламбера

то есть решение U в некоторой точке x_o в момент времени t_o зависит от значений начальной функции φ в двух точках на оси х: в точке (x_o — at_o) и в точке (x_o + at_o) (см. рис. 9).

Значение U равно среднему арифметическому значений начальной функции φ в точках (x_o — at_o) и (x_o + at_o). На рис. 9 изображена плоскость xOt, которая называется фазовой плоскостью. На оси х указаны точки (x_o — at_o, 0) и (x_o + at_o, 0), в которых начальные отклонения струны определяют величину отклонения струны в точке x_o в момент времени t_o. Эти точки являются точками пересечения прямых x — at = x_o — at_o и x + at = x_o + at_o с осью х. Указанные прямые называются характеристиками волнового уравнения. Треугольник с вершиной в точке (х_o, t_o) и основанием, которое получается при пересечении характеристик с осью х (см. рис. 9), называется характеристическим треугольником.

Используя такую интерпретацию формулы Даламбера, изобразим фазовую картину решения следующей задачи:

Замечание. На самом деле начальные отклонения струны не могут быть разрывными в точках х = -1 и х = 1, ведь струна не разрывается. Однако мы не слишком сильно погрешим против истинной картины распространения колебаний, если будем считать их кусочно постоянными. Дело в том, что, во-первых, рассматриваются очень малые колебания струны, и, во-вторых, малые изменения начальных значений незначительно влияют на решение задачи.

На рисунке 10 изображена фазовая плоскость x0t. Решение U(x,t) задачи отлично от нуля только в заштрихованных областях, причем начальное отклонение распространяется с одинаковой скоростью в двух противоположных направлениях – возникает прямая и обратная волны. Границы этих областей – это характеристики волнового уравнения: x — at = -1, x — at = 1, x + at = -1, x + at = 1.

Если рассмотреть процесс колебания некоторой фиксированной точки струны x = x_o, то нетрудно заметить, что она колеблется только в конечный промежуток времени: от момента до момента , то есть В остальное время точка x_o находится в покое. Говорят, что в момент t₁ через точку x = x_o проходит передний фронт волны, а в момент t₂ — задний фронт волны. Вообще, фронтом волны называется граница между возмущенной (колеблющейся) и невозмущенной областями среды (точками струны). Для прямой волны уравнение переднего фронта x — at = 1, а заднего фронта x — at = -1. Для обратной волны, соответственно, x + at = -1 — уравнение переднего фронта, а x + at = 1 — заднего фронта.

СЛУЧАЙ 2. Пусть начальное отклонение равно нулю, а начальная скорость отлична от нуля. Это означает, что начальные условия имеют вид

В этом случае решение задачи Коши называют волной импульса. Оно имеет вид (см. формулу Даламбера)

то есть решение U в некоторой точке x_o в момент времени t_o зависит от начальных скоростей ψ во всех точках отрезка [x_o — at_o , x_o + at_o] (см. рис 11). Значение U равно (интегральному) среднему значению начальной скорости на отрезке [x_o — at_o , x_o + at_o], умноженному на промежуток времени t.

На рис. 11 изображена фазовая плоскость x0t. Точки (x_o — at_o, 0) и (x_o + at_o, 0) являются точками пересечения характеристик x — at = x_o — at_o и x + at = x_o + at_o с осью х. В качестве примера приведем фазовую картину решения следующей задачи:

Рис. 12 описывает процесс колебания струны, которой сообщается начальная единичная скорость на отрезке -1

При вычислении интеграла всегда удобно представить себе характеристический треугольник с вершиной в точке, лежащей в соответствующей области (см. рис 12). Тогда значение U(x,t) будет определяться значениями начальной функции ψ(x) в основании характеристического треугольника.

2. В области 2 функция

3. В области 3 функция

4. В области 4 функция

5. В области 6 функция

Это решение в различные моменты времени можно изобразить на плоскости x0U (см. рис 13). Здесь для простоты положим a=1.

Графики функции U(x,t), изображенные на рис. 13, задают форму струны в различные моменты времени.

Видео:Уравнение колебания струны. Решение методом ДаламбераСкачать

Магия тензорной алгебры: Часть 14 — Нестандартное введение в динамику твердого тела

Видео:Математика без Ху!ни. Ряды часть 2. Признак Даламбера.Скачать

Введение

Динамика твердого тела — раздел механики, который в своё время задал четкий вектор развития этой науки. Это один из самых сложных разделов динамики, и задача интегрирования уравнения сферического движения для произвольного случая распределения массы тела не решена до сих пор.

В этой статье мы начнем рассматривать динамику твердого тела, применяя аппарат тензорной алгебры. Эта пилотная статья о динамике ответит на ряд фундаментальных вопросов, касающихся, например, такого важного понятия как центр масс тела. Что такое центр масс, что отличает его от остальных точек тела, почему уравнения движения тела составляют в основном относительно этой точки? Ответ на эти, и некоторые другие вопросы находится под катом.

Интегрирование уравнений движения этой детской игрушки — одна из до сих пор не решенных задач механики.

Видео:Формула ДаламбераСкачать

1. Старый, как мир, принцип Даламбера

Для начала рассмотрим движение материальной точки. Непосредственно из аксиом вытекает основное уравнение динамики точки

ускорение помноженное на массу есть векторная сумма приложенных к точке сил. И о силах, которые приложены к точке надо поговорить подробнее. В разделе механики, называемом аналитической механикой, силы, прикладываемые к точкам механической системе подлежат строгой классификации.

Силы, стоящие в правой части (1) разделяются на две группы

Активные силы. Этой группе сил можно дать следующее определение

Активными называют силы, величину которых можно определить из условия задачи

Говоря формальным языком, активная сила определяется вектор функцией

где — обобщенная координата точки; — обобщенная скорость точки. Из данного выражения видно, что начиная решать задачу о движении и имея начальные условия (момент времени, положение и скорость) можно сразу рассчитать активную силу.

Сила тяжести, упругости, Кулоновская сила взаимодействия заряда с электрическим полем, сила Ампера и сила Лоренца, сила вязкого трения и аэродинамического сопротивления — всё это примеры активных сил. Выражения для их расчета известны и эти силы можно посчитать, зная положение и скорость точки.

Реакции связей. Самые неприятные силы, которые только можно придумать. Напомню одну из аксиом статики, именуемую аксиомой о связях

Связи приложенные к телу можно отбросить, заменив их действие силой, или системой сил

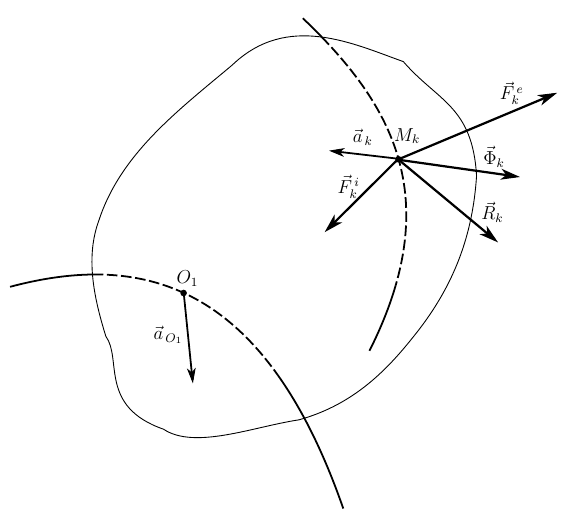
Изображенная на рисунке точка — не свободная точка. Её движение ограничено связью, условно представленной в виде некой поверхности, в пределах которых располагается траектория движения. Приведенная выше аксиома дает возможность убрать поверхность, приложив к точке силу , действие которой эквивалентно наличию поверхности. При этом данная сила не является известной заранее — её величина удовлетворяет ограничениям на положение, скорость и ускорение, накладываемыми связью, ну и, разумеется вектор реакции зависит от приложенных активных сил. Реакции связей подлежат определению в процессе решения задачи. К реакциям связей относится так же и сухое трение, наличие которого даже в простой задаче существенно осложняет процесс её решения.

Исходя из данной классификации, уравнение движения точки (1) переписывают в виде

где — равнодействующая активных сил, приложенных к точке; — равнодействующая реакций, наложенных на точку связей.

А теперь проделаем простейший фокус — ускорение с массой перенесем в другую часть уравнения (2)

и введем обозначение

Тогда, уравнение (2) превращается в

Сила, представляемая вектором (3) называется силой инерции Даламбера. А уравнение (4) выражает принцип Даламбера для материальной точки

Материальная точка находится в равновесии под действием приложенных к ней активных сил, реакций связей и сил инерции

Позвольте, о каком равновесии может идти речь, если точка движется с ускорением? Но ведь уравнение (4) есть уравнение равновесия, и приложив к точке силу (3) мы можем заменить движение точки её равновесием.

Достаточно распространен спор о том, являются ли силы инерции (3) физическими силами. В инженерной практике используется понятие центробежной силы, которая есть сила инерции, связанная с центростремительным (или осестремительным) ускорением, искривляющим траекторию точки. Моё личное мнение таково, что силы инерции есть математический фокус, продемонстрированный выше, позволяющий перейти к рассмотрению равновесия вместо движения с ускорением. Сила инерции (3) определяется ускорением точки, но оно, в свою очередь определяется действием на точку приложенных к ней сил, и в соответствии аксиоматикой Ньютона сила первична. Поэтому ни о какой «физичности» сил инерции говорить не приходится. Природа не знает активных сил, зависящих от ускорения.

Видео:Решение системы дифференциальных уравнений методом ЭйлераСкачать

2. Принцип Даламбера для твердого тела. Главный вектор и главный момент сил инерции

Теперь распространим уравнение (4) на случай движения твердого тела. В механике его рассматривают как неизменяемую механическую систему, состоящую из множества точек, расстояние между которыми в каждый момент времени остается неизменным. Все точки тела движутся по различным траекториям, но уравнение движения каждой точки соответствует (2)

Силы, действующие на конкретную точку можно разделить на внешние активные , реакции внешних связей , и внутренние силы , представляющие собой силы взаимодействия рассматриваемой точки с остальными точками тела (по сути — внутренние реакции). Все упомянутые силы есть равнодействующие соответствующей группы сил, приложенных к точке. Применим к этому уравнению Принцип Даламбера

где — сила инерции, приложенная к данной точке тела.

Теперь, когда все точки тела находятся в равновесии, мы можем воспользоваться условием равновесия твердого тела, которое дает нам статика

Твердое тело находится в равновесии под действием приложенной к нему системы сил, если главный вектор и главный момент этой системы сил, относительно выбранного центра O, раны нулю

Главный вектор системы сил — это векторная сумма всех сил, приложенных к телу. Сумма сил, приложенных к каждой точке тела определяется последним уравнением, поэтому складывая уравнения для всех точек, в левой его части получим главный вектор

При этом, сумма внутренних сил равна нулю, как следствие из третьего закона Ньютона. Аналогично вычисляем сумму моментов всех сил относительно выбранного произвольного центра O, что дает нам равный нулю главный момент системы сил

причем, как показывается в классическом курсе динамики, сумма моментов внутренних сил, приложенных к системе материальных точек, равна нулю, то есть . Уравнения (5) и (6) уже выражают принцип Даламбера применительно к твердому телу, но лишь с одной необходимой поправкой.

Число активных сил и реакций связей в уравнениях (5) и (6) конечно. Большинство слагаемых в соответствующих суммах равны нулю, ибо активные внешние силы и реакции внешних связей, вообще говоря, приложены лишь в некоторых точках тела. Чего нельзя сказать о силах инерции — силы инерции приложены к каждой точке тела. То есть сумма сил инерции, и сумма их моментов относительно выбранного центра есть суммы интегральные. Систему сил инерции принято сводить к главному вектору и главному моменту и мы можем написать, что

главный вектор и главный момент сил инерции, приложенных к твердому телу. Интегралы (7) и (8) берутся по всему объему тела, а — радиус вектор точки тела относительно выбранного центра O.

Исходя из данного соображения мы можем переписать (5) и (6) в окончательном виде

Уравнения (10) и (11) выражают принцип Даламбера для твердого тела

Теврдое тело находится в равновесии под действием приложенных к нему внешних сил, реакций связей, главного вектора и главного момента сил инерции.

По сути (10) и (11) есть форма записи дифференциальных уравнений движения твердого тела. Они довольно часто применяются в инженерной практике, однако с точки зрения механики, такая форма записи уравнений движения не является самой удобной. Ведь интегралы (7) и (8) можно вычислить в общем виде и придти к более удобным уравнениям движения. В этой связи (10) и (11) следует рассматривать как теоретическую основу построения аналитической механики.

Видео:Признак ДаламбераСкачать

3. На сцену выходят центр масс и тензор инерции

Вернемся к нашим тензорам и с их помощью вычислим интегралы (7) и (8) для общего случая движения твердого тела. В качестве центра приведения выберем точку O₁. Эта точка выбрана в качестве полюса и в ней определен локальный базис связанной с телом системы координат. В одной из прошлых статей мы определили тензорное соотношение для ускорения точки тела в таком движении

Умножив (12) на массу точки со знаком минус, мы получим силу инерции, приложенную к элементу объема твердого тела

Выражение (13) — ковариантное представление вектора силы инерции. Двойное векторное произведение в (12) перепишем в более удобной форме, используя тензор Леви-Чивиты и псевдовекторы угловой скорости и углового ускорения

Подставляем (14) в (13) и берем тройной интеграл по всему объему тела, учитывая, что угловая скорость и угловое ускорение одинаковы в каждой точке этого объема, то есть их можно вынести за знак интеграла

Интеграл в первом слагаемом — это масса тела. Интеграл во втором слагаемом более интересная штука. Вспомним одну из формул курса теоретической механики:

где — контравариантные компоненты радиус-вектора центра масс рассматриваемого тела. Не в даваясь в смысл понятия центра масс просто заменим интегралы в (15) в соответствии с формулой (16), учтя, что во втором слагаемом (15) используются ковариантные компоненты.

Ага, выражение (17) тоже нам знакомо, представим его в более привычной векторной форме

Первое слагаемое в (18) — сила инерции, связанная с поступательным движением тела вместе с полюсом. Второе слагаемое — центробежная сила инерции, связанная с осествемительным ускорением центра масс тела при его движении вокруг полюса. Третье слагаемое — вращательная составляющая главного вектора сил инерции, связанная с вращательным ускорением центра масс вокруг полюса. В общем-то всё находится в соответствии с классическими соотношениями теормеха.

Пытливый читатель скажет: «зачем применять тензоры для получения этого выражения, если в векторном виде оно было бы получено не менее очевидным способом?». В ответ я скажу, что получение формул (17) и (18) — это была разминка. Теперь мы получим выражение главного момента сил инерции относительно выбранного полюса, и тут тензорный подход проявляет себя во всей красе.

Возьмем уравнение (13) и умножим его векторно слева на радиус вектор точки тела относительно полюса. Тем самым мы получим момент силы инерции, приложенной к элементарному объему тела

Снова выполним подстановку (14) в (19), но не станем торопится брать интеграл

Не знаю как у вас, а у меня рябит в глазах, даже при моей привычности к таким формулам. Слагаемые расположены в более естественном порядке — переставлены местами вращательная и центробежная составляющие. Кроме того, от первого слагаемого ко второму возрастает сложность преобразующих выкладок. Будем упрощать их по очереди, сначала упростим первое, сразу взяв интеграл

Тут снова появился радиус вектор центра масс. Здесь ничего сложного — ускорение полюса у нас одно и мы вынесли его за знак интеграла. Интерпретацией займемся чуть позже, а пока преобразуем второе слагаемое (20). В нем мы можем выполнить свертку произведения тензоров Леви-Чивиты по немому индексу k

Здесь мы воспользовались свойством дельты Кронекера заменять свободный индекс вектора/ковектора при выполнении свертки. Теперь возьмет интеграл, учтя, что угловое ускорение постоянно для всего объема тела

Во как! Малопонятный «крокодил», путем формальных тензорных преобразований схлопнулся в компактную формулу. Я лукавлю, мы ввели новое обозначение:

Но это не просто абстрактная формула. По структуре выражения (24) видно, что оно отражает распределение массы тела вокруг полюса и называется оно — тензор инерции твердого тела. Эта величина имеет поистине фундаментальное значение для механики, и о ней мы поговорим подробнее, пока лишь скажу, что (24) — тензор второго ранга, компонентами которого являются осевые и центробежные моменты инерции тела в выбранной системе координат. Он характеризует инертность твердого тела при вращении. Обращаю внимание читателя и на то, как быстро мы получили выражение для тензора инерции, по сути действуя формальным способом. С векторными соотношения без ломки мозгов не обойтись, в этом я убедился на личном опыте.

Ну и наконец обратимся к последнему слагаемому (20). При взятии интеграла в нём тоже должен получится тензор инерции, и мы будем преобразовывать его таким образом, чтобы достичь этой цели. В этой части выражения (20) должно фигурировать соотношение между тензором инерции и угловой скоростью тела. Приступим, для начало свернув произведение тензоров Леви-Чивиты

Налицо существенное упрощение выражения — за счет свойств дельты Кронекера и того, что векторное произведение . Но тензора инерции в (25) не видно. С целью его получить проведем ряд эквивалентных преобразований

Здесь мы снова учли, что , воспользовались свойствами дельты Кронекера и операцией поднятия/опускания индексов при умножении на метрический тензор. И, теперь мы интегрируем (26)

Здесь мы снова видим тензор инерции:

с учетом которого получаем компактное выражение для составляющей главного момента сил инерции, связанного с центробежными силами

Выражение (27) эквивалентно векторно-матричному соотношению:

И хоть меня и переполняют пафосные фразы, отложу их на потом, а сейчас аккуратно выпишу итоговый результат в векторной форме.

В общем случае движения твердого тела главный вектор и главный момент сил инерции, приложенных к твердому телу, равны

А теперь все же восхитимся — не смотря на то, что вышеприведенные преобразования похожи на египетские иероглифы, они формальны, мы просто выполняли действия над индексами тензоров и использовали свойства тензорных операций. Нам не надо было упражняться с векторами, расписывать векторные операции в компонентах и сводить получившиеся проекции векторов к результатам матричных операций. Все матричные и векторные операции конечных выражение вышли у нас автоматически. К тому же, естественным образом получены такие фундаментальные характеристики как координаты центра масс тела и тензор инерции.

Читая лекции студентам я задался целью вывести (29) и (30) оперируя векторами. После того как я перевел стопку бумаги и изрядно поломав мозги я пришел к результату. Поверьте на слово — вышеприведенные преобразования просто семечки, в сравнении с тем, через что надо пройти не используя тензоров.

К тому же, выражения (29) и (30) получены нами для произвольного центра приведения сил, в качестве которого мы взяли полюс O₁. Эти выражения помогут нам понять что такое центр масс тела и его важность для механики.

Видео:2021 12 12 19 38 33 Принцип Даламбера для системы Видеоразбор решений задачСкачать

4. Особая роль центра масс

Используя формулы (29) и (30) вернемся к уравнениям (10) и (11) и, выполнив подстановку, придем к дифференциальным уравнениям движения твердого тела

Чем плохи эти уравнения? А тем, что они зависят друг от друга — ускорение полюса будет зависеть от углового ускорения и угловой скорости тела, угловое ускорение — от ускорения полюса. Вектор определяет положение центра масс тела по отношению к полюсу. А что если мы выберем полюс прямо в центре масс? Тогда ведь и уравнения (31), (32) примут более простой вид

Узнаете эти уравнения? Уравнение (33) — теорема о движении центра масс механической системы, а (34) — динамическое уравнение Эйлера сферического движения. И эти уравнения независимы друг от друга. Таким образом, центр масс твердого тела — это точка, относительно которой силы инерции приводятся к наиболее простому виду. Поступательное движение вместе с полюсом и сферическое вокруг полюса — динамически развязаны. Тензор инерции тела, вычисляется относительно центра масс и называется центральным тензором инерции.

Уравнения (33), (34) в зарубежной литературе называют уравнениями Ньютона-Эйлера, и, в настоящее время весьма активно используются для построения ПО, предназначенного для моделирования механических систем. В рамках цикла о тензорах мы ещё не раз о них вспомним.

Видео:3.1 Формула Даламбера, решение волнового уравнения на бесконечной прямойСкачать

Заключение

Прочитанная вами статья имеет две цели — в ней мы ввели базовые понятия динамики твердого тела и проиллюстрировали мощность тензорного подхода при упрощении громоздких векторных соотношений.

В дальнейшем мы подробнее остановимся на тензоре инерции и изучим его свойства. Погрузившись в дебри аналитической механики, сведем уравнения (31) — (34) к уравнениям движения в обобщенных координатах. В общем, рассказать ещё есть о чем. А пока, благодарю за внимание!

💥 Видео

Принцип Даламбера. Определение реакций связей механической системы.Скачать

Уравнения Лагранжа второго рода. Задача 1Скачать

§4.1. Принцип ДаламбераСкачать

Сеточные методы решения дифференциальных уравнений в частных производных.Скачать

Неоднородное уравнение колебания струныСкачать

Дифференциальные уравнения, 5 урок, Уравнение БернуллиСкачать

Формула Даламбера. Метод продолженийСкачать

Математика без Ху!ни. Ряды. Часть 1. Сумма ряда. Сходимость. Геометрическая прогрессия.Скачать

Уравнения Лагранжа второго родаСкачать