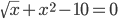Метод бисекций для решения нелинейных уравнений

Видео:Метод половинного деления решение нелинейного уравненияСкачать

Метод половинного деления (метод дихотомии или метод бисекции)

Теорема 2. Итерационный процесс половинного деления сходится к искомому корню ξ с любой наперед заданной точностью ε.
Доказательство: Рассмотрим последовательность чисел ξ_i являющихся приближением корня на i -ом шаге.
ξ_i=½(b_i+a_i), i=0,1.
где a₀=a; b₀=b; a_i;b_i — границы подынтервалов, в которых f(a_i)f(b_i) 0 мы ни задали, всегда можно найти такое n , что ч.т.д.
Графически метод дихотомии выглядит следующим образом

|f(c)|≤δ f(a)f(c) 10 = 1024 ≈ 10 3 раз. За 20 итераций (n=2) уменьшается в 2 20 ≈ 10 6 раз.

Пример №1 . Найти экстремум функции: y=5x 2 -4x+1 методом дихотомии, если ε=0.1, а исходный интервал [0,10].

• Решение
• Видео решение

Пример №3 . Методом бисекции найти решение нелинейного уравнения на отрезке [a,b] с точностью ε = 10 -2 . Выбрав полученное решение в качестве начального приближения, найти решение уравнения методом простой итерации с точностью ε = 10 -4 . Для метода простой итерации обосновать сходимость и оценить достаточное для достижения заданной точности число итераций.
sqrt(t)+x 2 = 10, a = 2.6, b = 3

Найдем корни уравнения:
Используем для этого Метод половинного деления (метод дихотомии)..
Считаем, что отделение корней произведено и на интервале [a,b] расположен один корень, который необходимо уточнить с погрешностью ε.
Итак, имеем f(a)f(b) 1 /₂(a+b) и вычисляем f(c). Проверяем следующие условия:
1. Если |f(c)| 1 /₂ n (b-a)
В качестве корня ξ. возьмем 1 /₂(a_n+b_n). Тогда погрешность определения корня будет равна (b_n – a_n)/2. Если выполняется условие:
(b_n – a_n)/2 1 /₂(a_n+b_n).
Решение.
Поскольку F(2.6)*F(3) 0, то a=2.8
Итерация 2.
Находим середину отрезка: c = (2.8 + 3)/2 = 2.9
F(x) = 0.113
F(c) = -0.487
Поскольку F(c)•F(x) 0, то a=2.825
Остальные расчеты сведем в таблицу.

Ответ: x = 2.8438; F(x) = -0.2267
Решение было получено и оформлено с помощью сервиса Метод Ньютона онлайн

Пример №2 . Локализовать корень нелинейного уравнения f(x) = 0 и найти его методом бисекции с точностью ε₁ = 0,01. Выбрав полученное решение в качестве начального приближения, найти решение уравнения методом простой итерации с точностью ε₂ = 0,0001. Для метода простой итерации обосновать сходимость и оценить достаточное для достижения заданной точности ε₂ число итераций.

Видео:14 Метод половинного деления Ручной счет Численные методы решения нелинейного уравненияСкачать

Метод бисекции

Метод бисекции или метод деления отрезка пополам — простейший численный метод приближённого нахождения корня уравнения.

Калькулятор, который находит приближенное решение уравнения методом бисекции или методом деления отрезка пополам. Небольшая теория под калькулятором.

Метод бисекции

Метод бисекции

Существует довольно очевидная теорема: «Если непрерывная функция на концах некоторого интервала имеет значения разных знаков, то внутри этого интервала у нее есть корень (как минимум, один, но может быть и несколько)». На базе этой теоремы построено несколько методов численного нахождения приближенного значения корня функции. Обобщенно все эти методы называются методами дихотомии, т. е. методами деления отрезка на две части (необязательно равные).

Здесь уже были рассмотрены Метод хорд и Метод секущих, теперь дошла очередь и до самого простого метода дихотомии, называемого методом бисекции, или методом деления отрезка пополам. Как следует из названия, именно в этом методе отрезок делится каждый раз на две равные части. Середина отрезка считается следующим приближением значения корня. Вычисляется значение функции в этой точке, и, если критерий останова не достигнут, выбирается новый интервал. Интервал выбирается таким образом, чтобы на его концах значения функции по прежнему имели разный знак, то есть чтобы он по прежнему содержал корень. Такой подход обеспечивает гарантированную сходимость метода независимо от сложности функции — и это весьма важное свойство. Недостатком метода является то же самое — метод никогда не сойдется быстрее, т. е. сходимость метода всегда равна сходимости в наихудшем случае.

Итерационная формула проста:

Метод бисекции является двухшаговым, то есть новое приближение определяется двумя предыдущими итерациями. Поэтому необходимо задавать два начальных приближения корня.
Метод требует, чтобы начальные точки были выбраны по разные стороны от корня (то есть корень содержался в выбранном интервале).

В качестве критерия останова берут один из следующих:

— значение функции на данной итерации стало меньше заданого ε.

— изменение хk в результате итерации стало меньше заданого ε. Поскольку интервал на каждом шаге уменьшается в два раза, вместо проверки x можно рассчитать количество требуемых итераций.

Видео:Численное решение уравнений, урок 3/5. Метод хордСкачать

Метод деления отрезка пополам (метод бисекции)

Один из простейших методов нахождения корней нелинейных уравнений состоит в следующем. Допустим, что нам удалось найти отрезок [а, b], на котором расположено искомое значение корня (далее мы предполагаем, что х = с – единственный корень на отрезке [а, b], а если корней на [а, b] несколько, то в результате применения метода деления отрезка пополам и метода хорд (см. разд. 1.1.3) будет найдено приближенное значение одного из корней) х = с, т.е. .

В качестве начального приближения корня с0 принимаем середину этого отрезка: с0=(а+b)/2. Далее исследуем значения функции F(x) на концах отрезков [а, с0] и [с0, b], т.е. в точках а, с0, b. Тот из отрезков, на концах которого F(x) принимает значения разных знаков, содержит искомый корень; поэтому его принимаем в качестве нового отрезка [a1,b1]. Вторую половину отрезка [а, b], на которой знак F(x) не меняется, отбрасываем. В качестве первого приближения корня принимаем середину нового отрезка c1 = (a1+b1)/2 и т.д. Таким образом, k-е приближение вычисляем как

(1.2)

После каждой итерации отрезок, на котором расположен корень, уменьшается вдвое, а после kитераций он сокращается в 2kраз:

(1.3)

Пусть приближенное решение требуется найти с точностью до некоторого заданного малого числа ε > 0:

(1.4)

Взяв в качестве приближенного решения k-еприближение корня: , запишем (1.4) с учетом обозначения — сk в виде:

(1.5)

Из (1.2) следует, что (1.5) выполнено, если

(1.6)

Таким образом, итерационный процесс нужно продолжать до тех пор, пока не будет выполнено условие (1.6).

Метод деления отрезка пополам проиллюстрирован на рис. 1.1. Пусть для определенности F(a) 0. В качестве начального приближения корня примем с0 = (а + b)/2. Поскольку в рассматриваемом случае F(c0) 0 и F(b) > 0. Таким образом, с[с0, c1],а2=с0, b2 = с1. Аналогично находим другие приближения: с2=(с0+c1)/2и т.д. до выполнения условия (1.6).

Рис. 1.1. Метод деления отрезка пополам

В отличие от большинства других итерационных методов метод деления отрезка пополам всегда сходится, причем можно гарантировать, что полученное решение будет иметь любую наперед заданную точность (разумеется, в рамках разрядности компьютера). При применении этого метода нет необходимости приближенно определять момент достижения требуемой точности, пользуясь, например, условиями близости двух последовательных приближений (2.22) или (2.23) (записанными для скалярного случая). Вместо них применяется соотношение (1.6), гарантирующее выполнение (1.4).

Однако метод деления отрезка пополам довольно медленный. Вычислим число итераций N, требуемое для достижения точности ε. Для этого выясним, пользуясь (1.3), для каких kвыполнено условие (1.6), и возьмем в качестве N наименьшее из таких k. Окончательно получим

(1.7)

где Е(х) – целая часть числа х. Обычно для метода деления отрезка пополам N больше, чем для некоторых других методов, что не является препятствием к применению этого метода, если каждое вычисление значения функции F(x) несложно.

Итерационный процесс можно завершать и тогда, когда значение функции F(x) после k-й итерации станет меньшим по модулю ε, т.е.

(1.8)

Такое условие окончания итераций аналогично условию (2.24). Действительно, для уравнения (1.1) величина F(ck)есть невязка(см. разд. 2.2.2),полученная на k—йитерации.

На рис. 1.2 представлен алгоритм итерационного процесса нахождения корня уравнения (1.1) методом деления отрезка пополам. Здесь сужение отрезка осуществляется заменой границ а или bна текущее значение корня с. При этом значение F(a) вычисляют лишь один раз, поскольку нам нужен только знак функции F(x) на левой границе, а он в процессе итераций не меняется.

Рис. 1.2. Алгоритм метода деления отрезка пополам

💡 Видео

1,2 Решение нелинейных уравнений методом хордСкачать

Решение нелинейных уравнений методом хордСкачать

Решение нелинейного уравнения методом половинного деления (программа)Скачать

Метод половинного деления. ДихотомияСкачать

Метод Ньютона (метод касательных) Пример РешенияСкачать

Метод хордСкачать

10 Численные методы решения нелинейных уравненийСкачать

8 Метод половинного деления Calc Excel Численные методы решения нелинейного уравненияСкачать

Отделение корней уравнений аналитическим методом. Уточнение корней методом половинного деленияСкачать

1.1 Решение нелинейных уравнений метод деления отрезка пополам (бисекций) Мathcad15Скачать

Решение нелинейного уравнения методом хорд (секущих) (программа)Скачать

Метод половинного деления Ручной счет Численные методы решения нелинейного уравненияСкачать

6 Метод половинного деления C++ Численные методы решения нелинейного уравненияСкачать

Метод половинного деленияСкачать

Метод простых итераций пример решения нелинейных уравненийСкачать

Численные методы (1 урок)(Решение нелинейных уравнений. Метод дихотомии. Python)Скачать

5 Метод половинного деления Блок-схема Численные методы решения нелинейного уравненияСкачать