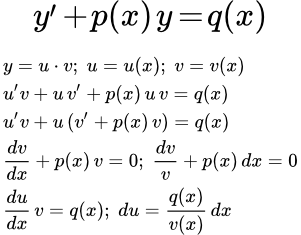Метод бернулли и лагранжа решения дифференциальных уравнений (6 видео)

Содержание

Метод Бернулли (введение двух функций). Линейные дифференциальные уравнения первого порядка
Метод введения двух функций (Бернулли)
Пример решения линейного дифференциального уравнения первого порядка методом Бернулли
14. Линейные неоднородные дифференциальные уравнения. Метод Бернулли
Дифференциальные уравнения Бернулли в примерах решений
💥 Видео

Видео:Метод Лагранжа & Метод Бернулли ★ Решение линейных неоднородных дифференциальных уравненийСкачать

Метод Бернулли (введение двух функций). Линейные дифференциальные уравнения первого порядка

Рассмотрим линейное неоднородное дифференциальное уравнение первого порядка:

Существует три способа решения этого уравнения:

Рассмотрим решение линейного дифференциального уравнения первого порядка методом Бернулли.

Видео:7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать

Метод введения двух функций (Бернулли)

Ищем решение исходного уравнения в виде произведения двух функций:
y = u · v
где u, v — функции от x . Дифференцируем:
y′ = u′ · v + u · v′
Подставляем в исходное уравнение:

Выносим u за скобки:
(1)
В качестве v возьмем любое, отличное от нуля, решение уравнения:
(2)
Это уравнение с разделяющимися переменными.

Разделяем переменные. Умножаем обе части уравнения на dx и делим на v

Интегрируем:

Постоянную C возьмем равной нулю, поскольку нам нужно любое, отличное от нуля, решение.

Потенцируем и опускаем знак модуля (Знак модуля сводится к умножению на постоянную ±1 ).

Подставим в (1) учитывая, что согласно (2), выражение в скобках равно нулю:

Отсюда

Интегрируем

Окончательно находим:

Видео:Уравнение Бернулли Метод БернуллиСкачать

Пример решения линейного дифференциального уравнения первого порядка методом Бернулли

Делаем подстановку:
y = u · v
где u, v — функции от x . Дифференцируем:
y′ = u′ · v + u · v′
Подставляем в исходное уравнение:

Выносим u за скобки:
(3)
В качестве v возьмем любое, отличное от нуля, решение уравнения:
(4) .
Это уравнение с разделяющимися переменными,
.
Разделяем переменные. Умножаем обе части уравнения на dx и делим на xv :

Интегрируем:

Постоянную C возьмем равной нулю, поскольку нам нужно любое, отличное от нуля, решение. По таблице интегралов, находим:

Или

Потенцируем и опускаем знаки модуля (Знак модуля сводится к умножению на постоянную ±1 ).

Подставим в (3) учитывая, что согласно (4), выражение в скобках равно нулю:

Отсюда

Интегрируем, применяя формулу :
.
Окончательно находим:
.

Общее решение уравнения:

Автор: Олег Одинцов . Опубликовано: 24-07-2012 Изменено: 27-02-2015

Видео:Метод Бернулли. Метод ЛагранжаСкачать

14. Линейные неоднородные дифференциальные уравнения. Метод Бернулли

(Якоб Бернулли (1654-1705) – швейцарский математик.)

Для интегрирования линейных неоднородных уравнений (Q(X)¹0) применяются в основном два метода: метод Бернулли и метод Лагранжа.

Суть метода заключается в том, что искомая функция представляется в виде произведения двух функций .

При этом очевидно, что — дифференцирование по частям.

Подставляя в исходное уравнение, получаем:

Далее следует важное замечание – т. к. первоначальная функция была представлена нами в виде произведения, то каждый из сомножителей, входящих в это произведение, может быть произвольным, выбранным по нашему усмотрению.

Например, функция может быть представлена как

и т. п.

Таким образом, можно одну из составляющих произведение функций выбрать так, что выражение .

Таким образом, возможно получить функцию U, проинтегрировав, полученное соотношение как однородное дифференциальное уравнение по описанной выше схеме:

Для нахождения второй неизвестной функции V подставим поученное выражение для функции U В исходное уравнение с учетом того, что выражение, стоящее в скобках, равно нулю.

Интегрируя, можем найти функцию V:

; ;

Т. е. была получена вторая составляющая произведения , которое и определяет искомую функцию.

Подставляя полученные значения, получаем:

Окончательно получаем формулу:

, С2 — произвольный коэффициент.

Это соотношение может считаться решением неоднородного линейного дифференциального уравнения в общем виде по способу Бернулли.

( Ларганж Жозеф Луи (1736-1813) — французский математик, през. Берлинской АН,

Поч. чл. Пет. АН (1776)).

Метод Лагранжа решения неоднородных линейных дифференциальных уравнений еще называют методом Вариации произвольной постоянной.

Вернемся к поставленной задаче:

Первый шаг данного метода состоит в отбрасывании правой части уравнения и замене ее нулем.

Далее находится решение получившегося однородного дифференциального уравнения:

Для того, чтобы найти соответствующее решение неоднородного дифференциального уравнения, будем считать постоянную С1 некоторой функцией от х.

Тогда по правилам дифференцирования произведения функций получаем:

Подставляем полученное соотношение в исходное уравнение

Из этого уравнения определим переменную функцию С1(х):

Подставляя это значение в исходное уравнение, получаем:

Таким образом, мы получили результат, полностью совпадающий с результатом расчета по методу Бернулли.

При выборе метода решения линейных дифференциальных уравнений следует руководствоваться простотой интегрирования функций, входящих в исходный интеграл.

Далее рассмотрим примеры решения различных дифференциальных уравнений различными методами и сравним результаты.

Пример. Решить уравнение

Сначала приведем данное уравнение к стандартному виду:

Применим полученную выше формулу:

Определение. Уравнением Бернулли Называется уравнение вида

Где P и Q – функции от Х или постоянные числа, а N – постоянное число, не равное 1.

Для решения уравнения Бернулли применяют подстановку , с помощью которой, уравнение Бернулли приводится к линейному.

Для этого разделим исходное уравнение на Yn.

Применим подстановку, учтя, что .

Т. е. получилось линейное уравнение относительно неизвестной функции z.

Решение этого уравнения будем искать в виде:

Пример. Решить уравнение

Разделим уравнение на Xy2:

Полагаем

Произведя обратную подстановку, получаем:

Пример. Решить уравнение

Разделим обе части уравнения на

Полагаем

Получили линейное неоднородное дифференциальное уравнение. Рассмотрим соответствующее ему линейное однородное уравнение:

Полагаем C = C(x) и подставляем полученный результат в линейное неоднородное уравнение, с учетом того, что:

Получаем:

Применяя обратную подстановку, получаем окончательный ответ:

Уравнения в полных дифференциалах (тотальные).

Определение. Дифференциальное уравнение первого порядка вида:

Называется Уравнением в полных дифференциалах, если левая часть этого уравнения представляет собой полный дифференциал некоторой функции

Интегрирование такого уравнения сводится к нахождению функции U, после чего решение легко находится в виде:

Таким образом, для решения надо определить:

1) в каком случае левая часть уравнения представляет собой полный дифференциал функции U;

2) как найти эту функцию.

Если дифференциальная форма Является полным дифференциалом некоторой функции U, то можно записать:

Т. е. .

Найдем смешанные производные второго порядка, продифференцировав первое уравнение по У, а второе – по Х:

Приравнивая левые части уравнений, получаем Необходимое и достаточное условие того, что левая часть дифференциального уравнения является полным дифференциалом. Это условие также называется Условием тотальности.

Теперь рассмотрим вопрос о нахождении собственно функции U.

Проинтегрируем равенство :

Вследствие интегрирования получаем не постоянную величину С, а некоторую функцию С(у), т. к. при интегрировании переменная У полагается постоянным параметром.

Определим функцию С(у).

Продифференцируем полученное равенство по У.

Откуда получаем:

Для нахождения функции С(у) необходимо проинтегрировать приведенное выше равенство. Однако, перед интегрированием надо доказать, что функция С(у) не зависит от Х. Это условие будет выполнено, если производная этой функции по Х равна нулю.

Теперь определяем функцию С(у):

Подставляя этот результат в выражение для функции U, получаем:

Тогда общий интеграл исходного дифференциального уравнения будет иметь вид:

Следует отметить, что при решении уравнений в полных дифференциалах не обязательно использовать полученную формулу. Решение может получиться более компактным, если просто следовать методу, которым формула была получена.

Пример. Решить уравнение

Проверим условие тотальности:

Условие тотальности выполняется, следовательно, исходное дифференциальное уравнение является уравнением в полных дифференциалах.

Определим функцию U.

;

Итого,

Находим общий интеграл исходного дифференциального уравнения:

Решение уравнений, не содержащих в одном случае аргумента Х, а в другом – функции У, ищем в параметрической форме, принимая за параметр производную неизвестной функции.

Для уравнения первого типа получаем:

Делая замену, получаем:

В результате этих преобразований имеем дифференциальное уравнение с разделяющимися переменными.

Общий интеграл в параметрической форме представляется системой уравнений:

Исключив из этой системы параметр Р, получим общий интеграл и не в параметрической форме.

Для дифференциального уравнения вида X = F(Y’) с помощью той же самой подстановки и аналогичных рассуждений получаем результат:

Уравнения Лагранжа и Клеро.

( Алекси Клод Клеро (1713 – 1765) французский математик

Ин. поч. член Петерб. АН )

Определение. Уравнением Лагранжа Называется дифференциальное уравнение, линейное относительно Х и У, коэффициенты которого являются функциями от Y’.

Для нахождения общего решение применяется подстановка P = Y’.

Дифференцируя это уравнение, c учетом того, что , получаем:

Если решение этого (линейного относительно Х) уравнения есть То общее решение уравнения Лагранжа может быть записано в виде:

Определение. Уравнением Клеро Называется уравнение первой степени (т. е. линейное) относительно функции и аргумента вида:

Вообще говоря, уравнение Клеро является частным случаем уравнения Лагранжа.

С учетом замены , уравнение принимает вид:

Это уравнение имеет два возможных решения:

или

В первом случае:

Видно, что общий интеграл уравнения Клеро представляет собой семейство прямых линий.

Во втором случае решение в параметрической форме выражается системой уравнений:

Исключая параметр Р, получаем второе решение F(x, y) = 0. Это решение не содержит произвольной постоянной и не получено из общего решения, следовательно, не является частным решением.

Это решение будет являться особым интегралом. ( См. Особое решение.)

Далее рассмотрим примеры решения различных типов дифференциальных уравнений первого порядка.

Пример. Решить уравнение с заданными начальными условиями.

Это линейное неоднородное дифференциальное уравнение первого порядка.

Решим соответствующее ему однородное уравнение.

Для неоднородного уравнения общее решение имеет вид:

Дифференцируя, получаем:

Для нахождения функции С(х) подставляем полученное значение в исходное дифференциальное уравнение:

Итого, общее решение:

C учетом начального условия Определяем постоянный коэффициент C.

Окончательно получаем:

Для проверки подставим полученный результат в исходное дифференциальное уравнение: верно

Ниже показан график интегральной кривой уравнения.

Пример. Найти общий интеграл уравнения .

Это уравнение с разделяющимися переменными.

Общий интеграл имеет вид:

Построим интегральные кривые дифференциального уравнения при различных значениях С.

С = — 0,5 С = -0,02 С = -1 С = -2

С = 0,02 С = 0,5 С = 1 С = 2

Пример. Найти решение дифференциального уравнения, удовлетворяющее заданным начальным условиям.

Это уравнение с разделяющимися переменными.

Общее решение имеет вид:

Найдем частное решение при заданном начальном условии У(0) = 0.

Окончательно получаем:

Пример. Решить предыдущий пример другим способом.

Действительно, уравнение может быть рассмотрено как линейное неоднородное дифференциальное уравнение.

Решим соответствующее ему линейное однородное уравнение.

Решение неоднородного уравнения будет иметь вид:

Тогда

Подставляя в исходное уравнение, получаем:

Итого

С учетом начального условия у(0) = 0 получаем

Как видно результаты, полученные при решении данного дифференциального уравнения различными способами, совпадают.

При решении дифференциальных уравнений бывает возможно выбирать метод решения, исходя из сложности преобразований.

Пример. Решить уравнение С начальным условием у(0) = 0.

Это линейное неоднородное уравнение. Решим соответствующее ему однородное уравнение.

Для линейного неоднородного уравнения общее решение будет иметь вид:

Для определения функции С(х) найдем производную функции У и подставим ее в исходное дифференциальное уравнение.

Итого

Проверим полученное общее решение подстановкой в исходное дифференциальное уравнение.

(верно)

Найдем частное решение при у(0) = 0.

Окончательно

Пример. Найти решение дифференциального уравнения

С начальным условием у(1) = 1.

Это уравнение может быть преобразовано и представлено как уравнение с разделенными переменными.

С учетом начального условия:

Окончательно

Пример. Решить дифференциальное уравнение с начальным условием у(1) = 0.

Это линейное неоднородное уравнение.

Решим соответствующее ему однородное уравнение.

Решение неоднородного уравнения будет иметь вид:

Подставим в исходное уравнение:

Общее решение будет иметь вид:

C учетом начального условия у(1) = 0:

Частное решение:

Пример. Найти решение дифференциального уравнения с начальным условием у(1) = е.

Это уравнение может быть приведено к виду уравнения с разделяющимися переменными с помощью замены переменных.

Обозначим:

Уравнение принимает вид:

Получили уравнение с разделяющимися переменными.

Сделаем обратную замену:

Общее решение:

C учетом начального условия у(1) = е:

Частное решение:

Второй способ решения.

Получили линейное неоднородное дифференциальное уравнение. Соответствующее однородное:

Решение исходного уравнения ищем в виде:

Тогда

Подставим полученные результаты в исходное уравнение:

Получаем общее решение:

Пример. Решить дифференциальное уравнение с начальным условием у(1)=0.

В этом уравнении также удобно применить замену переменных.

Уравнение принимает вид:

Делаем обратную подстановку:

Общее решение:

C учетом начального условия у(1) = 0:

Частное решение:

Второй способ решения.

Замена переменной:

Общее решение:

Видео:9. Метод вариации произвольной постоянной ( метод Лагранжа ). Линейные дифференциальные уравнения.Скачать

Дифференциальные уравнения Бернулли в примерах решений

Дифференциальным уравнением Бернулли называется уравнение вида

Таким образом, дифференциальное уравнение Бернулли обязательно содержит функцию y в степени, отличной от нуля и единицы.

В случае, если m = 0 , уравнение является линейным, а в случае, если m = 1 , уравнение является уравнением с разделяющимися переменными.

Дифференциальное уравнение Бернулли можно решить двумя методами.

Переходом с помощью подстановки к линейному уравнению.
Методом Бернулли.

Переход от уравнения Бернулли к линейному уравнению.

Уравнение делим на :

Обозначим . Тогда , откуда . Переходя к новой переменной, получим уравнение

которое является линейным дифференциальным уравнение первого порядка. Его можно решить методом вариации константы Лагранжа или методом Бернулли.

Решение методом Бернулли.

Решение следует искать в виде произведения двух функций y = u ⋅ v . Подставив его в дифференциальное уравнение, получим уравнение

Из слагаемых, содержащих функцию u в первой степени, вынесем её за скобки:

Приравняв выражение в скобках нулю, то есть

получим дифференциальное уравнение с разделяющимися переменными для определения функции v .

Функцию u следует находить из дифференциального уравнения

которое также является уравнение с разделяющимися переменными.

Пример 1. Решить дифференциальное уравнение Бернулли

Решение. Решим дифференциальное уравнение двумя методами.

1. Переход от уравнения Бернулли к линейному уравнению. Данное уравнение умножим на y³ :

Введём обозначение , тогда , и приходим к уравнению

Решим его методом Бернулли. В последнее уравнение подставим z = u ⋅ v , z‘ = u‘v + uv‘ :

Выражение в скобках приравняем нулю и решим полученное дифференциальное уравнение:

Полученную функцию v подставим в уравнение:

2. Методом Бернулли. Ищем решение в виде произведения двух функций y = u ⋅ v . Подставив его и y‘ = u‘v + uv‘ в данное дифференциальное уравнение, получим

Выражение в скобках приравняем нулю и определим функцию v :

Полученную функцию v подставим в уравнение и определим функцию u :

И, наконец, найдём решение данного дифференциального уравнения:

Пример 2. Решить дифференциальное уравнение Бернулли

Решение. Это уравнение, в котором m = −1 . Применив подстановку y = u ⋅ v , получим

Выражение в скобках приравняем нулю и определим функцию v :

Полученную функцию v подставим в уравнение и определим функцию u :

Таким образом, получаем решение данного дифференциального уравнения:

Пример 3. Решить дифференциальное уравнение Бернулли

Решение. Это уравнение можно решить, используя подстановку y = u ⋅ v . Получаем

Приравняем нулю выражение в скобках и решим полученное уравнение с разделяющимися переменными:

Подставляем v в данное уравнение и решаем полученное уравнение:

и проинтегрируем обе части уравнения:

Далее используем подстановку

Таким образом, получаем функцию u :

и решение данного дифференциального уравнения:

Пример 4. Решить задачу Коши для дифференциального уравнения

при условии .

Решение. Перепишем уравнение, перенося в левую сторону линейные слагаемые, а в правую — нелинейные:

Это уравнение Бернулли, которое можно решить, используя подстановку y = u ⋅ v , y‘ = u‘v + uv‘ :

Выражение в скобках приравняем нулю и решим дифференциальное уравнение с разделяющимися переменными:

Подставим функцию v в данное уравнение и решим полученное дифференциальное уравнение:

Вычислим каждый интеграл отдельно. Первый:

Второй интеграл интегрируем по частям. Введём обозначения:

Приравниваем друг другу найденные значения интегралов и находим функцию u :

Таким образом, общее решение данного дифференциального уравнения:

Используем начальное условие, чтобы определить значение константы:

Ищем частное решение, удовлетворяющее начальному условию:

В результате получаем следующее частное решение данного дифференциального уравнения:

И напоследок — пример с альтернативным обозначением производных — через дробь.

Пример 5. Решить дифференциальное уравнение Бернулли

Решение. Решим это уравнение первым из представленных в теоретической части методом — переходом к линейному уравнению. Разделив данное уравнение почленно на y³ , получим