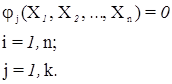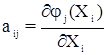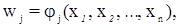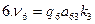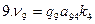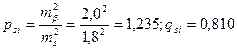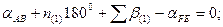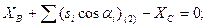Матрица коэффициентов условных уравнений поправок

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7

Такая наука, как геодезия тесно связана с измерениями, которые сопровождаются неизбежными ошибками. Если обозначим:

У – истинное значение измеряемой величины;

у – результат измерений;

— истинная ошибка.

то истинная ошибка может быть вычислена по формуле:

(15)

2 Виды ошибок измерений

По источникам и характеру ошибки делятся на грубые, систематические и случайные.

Грубые ошибки являются, как правило, следствие промахов, просчетов в измерениях, неисправностями инструментов и приборов, резким ухудшением внешних условий и пр. Они обнаруживаются при несоблюдении допусков и контролей и исключаются повторными измерениями.

Систематические – те, которые знаком или величиной однообразно повторяются в многократных измерениях. Их источниками являются неисправности в применяемых инструментах, неточная установка инструментов, личные физиологические особенности наблюдателя, влияние внешних факторов и т. п.

Примеры систематических ошибок:

— ошибка в измеренном значении длины линии на местности из-за отклонения мерной ленты от створа;

— ошибка в определении длины мерного прибора (ошибка компарирования).Эта ошибка постоянна и действует пропорционально измеренному расстоянию;

— систематическая ошибка нанесения шрихов лимба теодолита.

Влияние систематических ошибок сводят к допустимому минимуму путем тщательной поверки инструментов, применения соответствующей методики измерений, а также путем введения поправок в результаты измерений.

Некоторые рекомендации по уменьшению влияния систематических ошибок измерения:

— устанавливают закон появления систематической ошибки, после чего ошибку устраняют введением поправки в результаты измерений. Например, эталонирование мерного прибора и введение потом поправок за длину и температуру;

— применяют соответствующую методику измерений, чтобы систематические ошибки меняли знак. Например:

1) отсчитывание по диаметрально противоположным штрихам лимба, что приводит к исключению влияния эксцентриситета алидады;

2) перестановка лимба между приёмами на угол 180˚/n, где n-число приёмов ( при этом ослабевает влияние систематических ошибок штрихов лимба);

— используют определённую методику обработки результатов измерений. Например, углы и координаты вытянутого теодолитного хода уравнивают раздельно. Это ведёт к ослаблению влияния систематических ошибок угловых и линейных измерений.

Таким образом, будем считать, что результаты измерений содержат только слуайные ошибки, т. е. такие, размер и характер влияния которых на каждый отдельный результат измерения остается неизвестным.

3 Свойства случайных ошибок

Величину и знак случайных погрешностей установить нельзя.

Примеры случайных ошибок:

— ошибки отсчитывания по угломерному кругу;

— часть ошибки визирования, обусловленную колебаниями изображения;

— случайные ошибки нанесения штрихов лимба;

— влияние вибрации сигнала;

— ошибка отсчитывания по нивелирной рейке;

— ошибка за округление чисел при вычислениях.

Если результаты измерений содержат только случайные ошибки (грубые и систематические исключают), то

Чем ближе результат измерений к истинному значению, тем он точнее. Чем меньше ошибки, тем выше точность.

4 Обработка рядя равноточных измерений.

По точности результаты измерений разделяют на равноточные и неравноточные.

Под равноточными понимают однородные результаты, полученные при измерениях одним и тем же инструментом, одинаковым числом приемов, одним и тем же или равноценными методами и в одинаковых условиях.

5 Критерии оценки точности результатов измерений.

В геодезии необходиом уметь оценивать точность результатов измерений. Основным критерием точности в геодезии является средняя квадратическая ошибка (СКО). Ее математическое выражение:

, (16)

то есть квадрат СКО равен математическому ожиданию квадрата истинной ошибки.

Для оценки точности отдельного измерения применяется формула Гаусса:

или (17)

— случайная ошибка, тоже истинная, но

θ- истинная ошибка в более широком смысле. Она может состоять из случайной и систематической частей.

СПРАВКА: (1777 – 1855гг) – немецкий математик. Автор работ по астрономии. геодезии. физике. Разработал математические основы высшей геодезии, вычисляя погрешности при измерениях, разработал метод наименьших квадратов.

Кроме основной характеристики m, характеризующей влияние случайных ошибок на результаты измерений. иногда применяют дополнительную характеристику – среднюю ошибку

,

но СКО имеет ряд преимуществ по сравнению со средней квадратической погрешностью:

— на величину СКО сильнее влияют большие по абсолютной величине ошибки;

— СКО – устойчивая характеристика, даже при небольшом числе измерений даёт надёжные результаты.

Если — среднее арифметическое или арифметическая средина, то СКО арифметической средины М находится по формуле

где n – число измерений;

m – СКО одного измерения.

Для решения практических задач используется предельная ошибка ∆пред. Для серии ошибок в качестве ∆пред принимается утроенная СКО.

Это допуск, предел, больше которого не должно быть ошибки.

На практике во многих работах для повышения требований к точности измерений за предельную ошибку принимают удвоенную СКО.

Все приведённые выше ошибки называются абсолютными ошибками. Кроме абсолютных бывают относительные ошибки fотн, которыми называют отношение абсолютной ошибки к среднему значению измеряемой величины. Относительная ошибка выражается дробью, числитель которой равен 1, а знаменатель – отношение среднего значения измеряемой величины к абсолютной ошибке.

Приведенная выше формула Гаусса 17 применима для случаев, когда известны истинные значения измеряемых величин (или истинные ошибки). Эти случаи в практике редки. Известны они могут быть например, при моделировании, или за истинные значения принимают результаты измерений более высокой точности.

6 Арифметическая средина и ее средняя квадратичная ошибка

Как правило, истинные значения измеряемых величин неизвестны, но из измерений можно получить наиболее надежный результат – арифметическую средину по формуле:

(18)

=

Вычислив уклонение отдельных измерений от арифметической средины

, (19)

можно СКО одного измерения определить по формуле Бесселя:

(20)

Справка: (1784 – 1846гг) – немецкий астроном. член Берлинской АН. Он один из первых определил расстояние до звёзд. Реформировал методы учёта инструментальных и других ошибок, что повысило точность астрономических измерений.

7Средние квадратичные ошибки функций измеренных величин.

Формулы Гаусса и Бесселя определяют СКО непосредственно измеренных величин. Если определяемая величина является функцией других непосредственно измеряемых величин, то СКО функции может быть найдена по формуле:

где — СКО функции;

— функция многих независимых аргументов ;

— частные производные от функции по каждой переменной (результату измерений);

— СКО каждого результата измерений.

8 Неравноточные измерения.

9 Понятие о весе.

На практике часто производятся неравноточные измерения, которые выполнены в различных условиях, приборами различной точности, различным числом приемов и т. д. В этом случае уже нельзя ограничиваться простым арифметическим средним, а необходимо учитывать степень надежности каждого результата измерений. Надежность результата, выраженная числом, называется его весом. Чем надежнее результат, тем больше его вес. Следовательно, вес связан с точностью результата измерения, которая характеризуется СКО. Поэтому вес результата измерения принимают обратно пропорциональным квадрату СКО, то есть:

, (22)

где — некоторая постоянная величина, коэффициент пропорциональности;

— СКО измерения.

Таким образом, вес – относительная характеристика точности измерений. Использование веса вместо СКО облегчает. упрощает формулы математической обработки в случае неравноточных измерений. Необходим вес и потому, что более точные измерения в большей степени должны влиять на окончательный результат. (Для облегчения задачи отыскивания весов обычно вес какого-либо результата принимают за единицу и относительно его вычисляют веса остальных неизвестных.)

Если вес результат какого-либо измерения принять равным единице, а СКО измерения его обозначить через , то общее выражение веса примет вид:

, (23)

где — ср. кв. ош-ка единицы веса.

В практике геодезических работ в качестве весов принимают:

— при обработке результатов угловых измерений одним и тем же прибором – величины, пропорциональные количеству измерений каждого угла; для суммы углов в ходе, имеющем ni вершин,

— при обработке линейных измерений одним и тем же мерным прибором вес вычисляется по формуле

где si – длина линии;

— при обработке превышений из геометрического нивелирования — величины, обратно пропорциональные длине ходов или числу станций;

— при тригонометрическом нивелировании вес вычисляется по формуле

где si – расстояние между пунктами.

Принципы уравнивания геодезических сетей

1 Уравнивание геодезических сетей по МНК коррелатным способом.

2 Средняя квадратичная ошибка единицы веса

Геодезические измерения характерны тем, что их всегда больше, чем необходимо для определения искомых величин. Необходимыми называют такие измерения, которые позволяют однократно, бесконтрольно найти определяемые величины. Избыточными измерениями называются те, которые выполняют сверх необходимых. Например, для решения треугольника измеряют три угла, тогда как было бы достаточно измерить два угла.

Избыточные измерения позволяют:

— проконтролировать результаты измерений;

— в среднем повысит точность определяемых величин;

— выполнить оценку точности этих величин.

Число избыточных измерений определяется по формуле , (24)

где — число всех измерений в сети;

— число необходимых измерений.

Геодезические измерения ведутся в создаваемых на местности геодезических построениях, истинные элементы которых, в том числе и измеряемые, связаны между собой Математическими зависимостями.

Каждое избыточное измерение приводит к появлению математического соотношения с другими измеренными величинами. Неизбежные ошибки в измерениях приводят к появлению невязок в этих соотношениях. Для устранения невязок необходимо уравнивание результатов измерений.

Уравнивание – это математическая обработка результатов измерений, позволяющая:

— найти наиболее надежные (вероятнейшие) значения неизвестных с оценкой точности полученных результатов;

— исключить все математические противоречия в зависимостях, существующих между измеряемыми величинами.

ВЫВОД: сама задача уравнивания может быть поставлена только при наличии в сети избыточных измерений.

Целью уравнивания является:

— нахождение таких поправок к результатам измерений, которые не только компенсировали бы невязки, но и наилучшим образом приблизили уравненные значения измеренных величин к их истинным значениям;

— повышение точности всех измеренных величин;

— выполнение оценки точности по материалам уравнивания.

Может быть найдено множество систем поправок (множество вариантов), ликвидирующих невязки, но только одна система поправок позволяет найти вероятнейшие (т. е. наиболее приближённые к истинным) значения определяемых величин (и их функций).

Такая система поправок находится под условиями 25 и 26:

— для равноточных измерений,

(условие Лежандра) (25)

-для неравноточных измерений)

(условие Гаусса) (26)

Первое условие – сумма квадратов поправок в непосредственные измерения должна быть минимальной.

Второе условие – сумма произведений квадратов поправок на веса соответствующих результатов измерений должна быть минимальной.

Уравнивание под условиями 25 и 26 называют уравниванием по методу наименьших квадратов (МНК), а условия (25) и (26) – принципом наименьших квадратов.

Уравнивание по МНК – строгое. Другие способы нахождения поправок – приближённое уравнивание.

Для решения задачи уравнивания по МНК применяются два основных способа:

— коррелатный, основанный на способе Лагранжа с неопределенными множителями для нахождения условного экстремума;

— параметрический – способ абсолютного экстремума, при котором все измеренные величины представляют в виде функций некоторых независимых неизвестных параметров.

Существуют также комбинированные способы уравнивания – коррелатный с дополнительными неизвестными и параметрический с избыточными параметрами.

1 Уравнивание геодезических сетей по МНК коррелатным способом

Пусть выполнено измерений их которых — необходимых.

— результаты измерений;

— истинные значения измеренных величин;

— установленная система весов результатов измерений;

— обратные веса.

Связь между ними может быть выражена следующими соотношениями:

, (27)

где

— случайные ошибки;

. (28)

Число избыточных измерений , где .

Каждое избыточное измерение приводит к математическому соотношению между истинными значениями измеренных величин, т. е. в геодезической сети возникает условий:

, (29)

где

( т. е. здесь r функций: ).

Эта исходная система условных уравнений связи включает только независимые уравнения, число которых равно

Вследствие неизбежных ошибок в измерениях, эти же функции, но от измеренных величин примут вид:

где — невязки.

Это выражение называется системой условных уравнений связи от измеренных значений.

(31)

Отдельные ошибки неизвестны, но их совокупность (сумма) в каждом условии может быть вычислена.

Необходимо найти такие поправки к результатам измерений, которые ликвидируют невязки, то есть должно выполняться равенство:

, (32)

где поправки к результатам измерений;

Уравненные результаты измерений находят по формуле:

(33)

Тогда система условных уравнений связи от уравненных значений примет вид:

(34)

где

В правой части опять нули, т. к. невязки компенсировались поправками.

Систему (34) приводят к линейному виду, раскладывая каждое уравнение в ряд Тейлора, и пренебрегая при этом малыми (нелинейными) членами разложения:

Первое слагаемое согласно формуле (30) является невязкой , поэтому выражение (35) примет вид:

Обозначим частные производные от первой функции буквой , от второй —, от третьей —и т. д. То есть:

, ,…,;

, ,…, (37)

, ,…,

С учетом (37) система (36) примет вид:

(38)

Это система условных уравнений поправок. В ней:

— невязки;

— коэффициенты при поправках;

— неизвестные поправки, которые надо найти, решив систему (38).

Так как в системе (38) число уравнений меньше числа неизвестных поправок , то такая система имеет множество решений, т. е. не решается однозначно. Чтобы из множества вариантов выбрать один, наилучший, необходимо поставить дополнительное условие. Это условие:

(39)

является принципом наименьших квадратов.

Вывод нормальных уравнений коррелат представляется в матричной форме. Система (38) условных уравнений поправок

решается под условием (39) МНК

,

где — матрица коэффициентов при поправках условных уравнений поправок;

— вектор поправок;

— трансформированный вектор поправок;

— вектор свободных членов;

— матрица весов результатов измерений;

Используя метод Лагранжа с неопределенными множителями, называемыми в геодезии коррелатами, представленными в виде вектора коррелат (40)

составляют функцию Лагранжа (41)

чтобы найти min, находят производную от этой функции (42)

, (43)

(44)

где — трансформированная матрица коэффициентов при поправках;

— вектор коррелат.

Полагая, что , как симметричная матрица, получим коррелатное уравнение поправок, выражающее поправки в виде функций коррелат

(45)

— матрица обратных весов результатов измерений;

— обратный вес результата измерений;

— единичная матрица – т. е. уравнение (45) можно представить в виде

(46)

Выражение (46) является коррелатным уравнением поправок.

Подставив (46) в (38), получают систему нормальных уравнений коррелат:

(47)

,

где — матрица коэффициентов нормальных уравнений.

Коэффициенты, стоящие на главной диагонали, называются квадратичными, они всегда положительны, остальные – неквадратичные.

(48)

В системе нормальных уравнений коррелат (48) — неизвестные коррелаты. Их число r, как и число уравнений, поэтому система (48) решается однозначно.

Способы решения могут быть различны:

— по схеме Гаусса;

— методом исключения, когда из последнего уравнения выражается последнее неизвестное, подставляется в предыдущее уравнение и т. д.;

— на ЭВМ, по готовым программам.

Из решения нормальных уравнений находят коррелаты , а по ним поправки:

(49)

Выражение (49) называется коррелатным уравнением поправок.

Контролем вычисления поправок является равенство:

(50)

После этого вычисляют уравненные значения результатов измерений

, () (51)

и делают контроль уравнивания путем подстановки уравненных измерений в условные уравнения связи

(52)

2 Средняя квадратическая ошибка единицы веса

Оценка точности по результатам уравнивания, то есть по поправкам, может быть выполнена по формуле:

, (53)

где — средняя квадратическая ошибка единицы веса, то есть ошибка измерения с весом .

Чтобы оценить какой-либо элемент сети (отметку, координату, угол и т. д.) необходимо составить функцию, то есть математически выразить этот элемент.

(54)

где — средняя квадратическая ошибка функции;

— вес функции.

1 Уравнивание одиночного нивелирного хода коррелатным способом

Рассмотрим нивелирный ход

Рисунок 9 — Нивелирный ход

— исходные пункты;

— отметки исходных пунктов;

— измеренные превышения;

— длины секций;

— определяемые пункты, отметки которых необходимо найти.

Уравнивание нивелирного хода начинается с подсчета числа избыточных измерений по формуле

(55)

В ходе, представленном на рисунке 9, число измеренных превышений . Число необходимых измерений — по числу определяемых пунктов. Поэтому .

Контроль вычисления производится по формуле , (56)

где — число замкнутых полигонов;

— число исходных пунктов.

Таким образом, в нивелирном ходе возникает только одно условие и соответственно одно условное уравнение связи:

(57)

где — невязка.

Так как , то, согласно общей теории уравнивания, составляется одно нормальное уравнение коррелат

, (58)

где — обратные веса;

при , обратные веса ;

— коэффициенты при поправках условного уравнения поправок

(59)

Коэффициенты находятся как частные производные от функции по результатам измерений , т. е. , ,…, .

Видео:Матрица интенсивностей. Система уравнений КолмогороваСкачать

Коррелатный способ уравнивания

Коррелатный способ основан на использовании функциональной связи между собой элементов геодезических построений X_i (i = 1, n). Эти уравнения связи называются условными уравнениями:

При коррелатном способе уравнивания вначале составляется система условных уравнений AV + W = 0,

где А – матрица коэффициентов системы условных уравнений;

V – вектор поправок в измеренные значения элементов сети;

W – вектор невязок условных уравнений.

При этом коэффициенты a_ij условных уравнений поправок определяются по формуле:

а невязки уравнений – по формуле:

где x_i (i = 1, n) – измеренные значения элементов геодезических построений.

При известной весовой матрице Р вначале вычисляют обратную весовую матрицу Q = P -1 , а затем от системы условных уравнений переходят к системе нормальных уравнений:

Определив коррелаты К = — (AQA T ) W, вычисляют поправки V = QA T K и уравненные значения измеренных элементов сети x* = x + v,

где х* – вектор уравненных значений;

х – вектор измеренных значений элементов геодезических построений.

Дата добавления: 2016-06-02 ; просмотров: 1885 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Коррелатный способ. Решение системы условных уравненийСкачать

Примеры коррелатного способа уравнивания

В этом разделе приводятся примеры уравнивания некоторых геодезических построений. В примерах рассматривается алгоритм решения задачи уравнивания для разных вариантов геодезических построений со сравнительно небольшим числом измеренных величин, как это часто имеет место, например, в практике геодезических и маркшейдерских работ на земной поверхности при создании опорных сетей либо в горных выработках при обработке результатов измерений в системах полигонометрических ходов. Уравнивание систем нивелирных ходов обычно производится при точных и высокоточных измерениях, например, при наблюдениях за деформациями горных выработок и наземных сооружений, что тоже имеет место и в практике геодезических и маркшейдерских работ.

В примерах рассмотрены сравнительно простые схемы геодезических построений, однако принцип расчётов и в сложных системах точно такой же, как и в простых.

137.1. Уравнивание углов в полигоне

В полигоне, состоящем из четырёх вершин (рис. 14.7), неравноточно измерены горизонтальные углы: А = β₁ , В = β₂ , С = β₃ , D = β₄ (табл. 14.4).

Выполнить уравнивание углов без учёта измерения длин сторон.

Предварительно найдем веса p_i и обратные веса q_i, приняв м (см. табл. 14.4) без учёта величин измеренных углов, считая их практически примерно одинаковыми (значения весов определяются по условию возможной погрешности в направлениях из-за центрирования теодолита; для веса угла применяется правило сложения обратных весов направлений):

, (14.91)

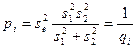
где s₁ и s₂ – стороны, образующие данный угол.

Шаг 1. Общее число измеренных величин n = 4, число необходимых измерений k = 3, число избыточных измерений r = 1.

Шаг 2. Составим условное уравнение (условие сумм углов полигона).

Всего одно уравнение, поскольку r = 1.

Шаг 3. Приводим условное уравнение к линейному виду, для чего продифференцируем его и найдем частные производные функции по аргументам β_i . Очевидно, что

Составим матрицу коэффициентов a_ij со строкой обратных весов q_i (таблица 14.5).

Рис. 14.7. Уравнивание углов в полигоне.

Матрица коэффициентов, весов и обратных весов

Свободный член уравнения

Шаг 4. Найдём коэффициенты b_jj нормальных уравнений (в данном случае – уравнений коррелат):

, (14.92)

. (14.93)

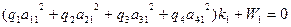
Для приведенного примера, с учётом значений a_ij и q_i , 13,266 k₁ + 7 = 0, откуда k₁ = — 0,528.

Шаг 5. Составляем условное уравнение поправок

(14.94)

и формулы для вычисления поправок (с вычислением их значений):

Контроль по формуле (14.94): условие выполнено! (проверьте сами). Отступление при округлениях значений поправок на 0,1″ является допустимым.

Вспомните загадку, которая прозвучала в начале этой главы. А если забыли, то возвратитесь к этому началу. Вот оно, что «под конец тонко» — это и есть хвостик решения всей задачи уравнивания: маленькие поправочки в измеренные величины. Ну а что тут было зелено, да посерёдке толсто – это уж понятно из решения данной задачи. Правда, приведенная задача – одна из самых простых. Дальше будет корнеплод посложнее. Но, всему своё время. А сейчас – закончим решение приведенной задачи.

Шаг 6. Вычисляем уравненные значения углов:

β₁ ‘ = 80° 16′ 44,3″ – 2,4″ = 80° 16′ 41,9″; β₂ ‘ = 91° 45′ 00,7″ – 1,1″ = 91° 44′ 59,6″;

β₃ ‘ = 69° 25′ 56,8″ – 1,2″ = 69° 25′ 55,6″; β₄ ‘ = 118° 32′ 25,2″ – 2,4″ = 181° 32′ 22,8″.

Контроль: подстановка уравненных значений углов в уравнение (14.91) – условие выполнено! (проверьте это условие).

Очевидно, что при равноточных измерениях углов для них были бы получены одинаковые поправки, т.е. невязка была бы распределена поровну во все углы.

137.2. Уравнивание системы нивелирных ходов с несколькими узловыми точками

На местности пройдена система нивелирных ходов с четырьмя узловыми точками 1, 2, 3 и 4 (рис. 14.8). В результате измерений образовано 9 секций, превышения в которых по указанному направлению приведены непосредственно на схеме. Указаны также высоты исходных реперов Р10, Р20 и Р30. В табл. 14.6 приведены длины ходов в секциях и значения весов и обратных весов превышений в секциях, вычисленные по формулам:

Рис. 14.8. Схема нивелирных ходов с четырьмя узловыми точками.

, (14.95)

где

Требуется определить уравненные значения высот узловых точек.

Шаг 1. Общее число измерений n = 9, число необходимых измерений k = 4, число избыточных измерений r = 5.

Шаг 2. Составим r = 5 условных уравнений:

Шаг 3. Приведём условные уравнения к линейному виду, продифференцировав их по аргументам h_i. Получим коэффициенты a_ij условных уравнений поправок:

Составим матрицу коэффициентов a_ij со строкой обратных весов q_i (табл. 14.7).

Матрица коэффициентов и обратных весов

Вычислим свободные члены (в мм), подставив в уравнения (14.96) измеренные значения h_i в секциях:

Шаг 4. Найдём по формулам (14.88) коэффициенты b_jj нормальных уравнений коррелат:

(14.97)

После подстановки значений a_ij и q_i в уравнения (14.97) получим исходные нормальные уравнения коррелат:

Из решения системы уравнений (14.98) одним из способов получим:

Контроль вычисления коррелат выполняем подстановкой их значений в исходные уравнения (14.98):

1. 2,18 (-2,137) – 1,08 (-11,552) + 0,42 (-1,945) – 7 = + 0,001;

2. -1,08(-2,137) + 2,79(-11,552) + 1,32(+9,606) + 0,39(-1,945) + 18 = -0,001;

3. 1,32(-11,552) + 3,86(+9,606) + 1,51(-3,882) – 16 = — 0,031;

4. 1,51(+9,606) + 4,42(-3,882) + 1,72(-1,945) + 6 = +0,001;

5. 0,42(-2,137) + 0,39(-11,552) + 1,72(-3,882) + 2,53(-1,945) + 17 = -0,001.

Сравнительно большее невыполнение условия мы видим в уравнении 3. Это вызвано погрешностями округлений. При вычислении с большими значащими цифрами этого не наблюдалось бы. При этом результаты вычислений принимаем удовлетворительными, поскольку поправки в измеренные значения превышений для данных условий будут в дальнейшем округляться до 1 мм, а вычисления проведены с большим запасом точности.

Шаг 5. Составляем условные уравнения поправок v_i, пользуясь формулами (14.86) и табл. 14.7:

(14.99)

1. v₁ = 0,42 ∙1∙ (-2,137) + 0,42∙1∙ (-1,945) = — 1,714 = — 2 мм;

2. v₂ = 0,68 ∙ (-1) ∙ (-2,137) = + 1,453 = + 1 мм;

3. v₃ = 1,08 ∙ 1 ∙ (2,137) + 1,08 ∙ (-1) ∙ (-11,552) = +10,168 = + 10 мм;

4. v₄ = 0,39 ∙ 1 ∙ (-11,552) + 0,39 ∙1 ∙ (-1,945) = — 5,264 = — 5 мм;

5. v₅ = 1,32 ∙1∙ (-11,552) + 1,32 ∙ 1 ∙ (+9,606) = — 2,569 = — 3 мм;

6. v₆ = 1,03 ∙1 ∙ (+9,606) = + 9,894 = + 10 мм;

7. v₇ = 1,51 ∙ 1 ∙ (+9,606) + 1,51 ∙1 ∙ (-3,882) = + 8,643 = + 9 мм;

8. v₈ = 1,72 ∙ 1 ∙ (-3,882) + 1,72 ∙ 1 ∙ (-1,945) = — 10,022 = — 10 мм;

9. v₉ = 1,19 ∙ (-1) ∙ (-3,882) = + 4,620 = + 5 мм.

Контроль вычисления поправок можно выполнить по формулам (14.96), подставив в них вместо превышений значения поправок (суммы поправок должны быть равны значениям соответствующих невязок с обратным знаком):

Шаг 6. Вычисляем уравненные значения превышений в секциях и контролируем уравнивание по выполнению условия (14.96):

h₆ ‘= + 5338 + 10 = + 5348 мм;

Подстановка в уравнения (14.96) подтверждает выполнение указанного условия.

Вычисляем уравненные значения высот узловых точек 1, 2 , 3 и 4:

Контроль вычислений здесь можно выполнить вторичным получением высот искомых точек по другим направлениям. Должны получиться те же результаты. Например, H₁ = H_P30 – h₈‘ – h₄‘ = 85,301 – 4,629 + 1,248 = 81,920 м.

137.3. Уравнивание системы полигонометрических ходов с двумя узловыми точками

Уравнивание таких систем полигонометрических ходов аналогично уравниванию как одиночного полигонометрического хода, так и системы полигонометрических ходов с одной узловой точкой. В такой системе (рис. 14.9) образуется три независимых полигонометрических хода [(1), (2), (3)], в которых возникает по три условия: три условия дирекционных углов и шесть условий координат, т.е. получается девять условных уравнений.

Рис. 14.9. Система полигонометрических ходов с двумя узловыми точками.

В табл. 14.8, 14.9 и 14.10 приведены необходимые исходные данные для решения задачи уравнивания, заключающейся в определении уравненных значений координат точек 1, 2, 3, M, N, а также уравненного значения дирекционного угла узловой линии MN. (В данном примере узловые точки M и N образуют и узловую линию).

Часто между узловыми точками прокладывают полигонометрический ход в две и более линии. Тогда понятие узловой линии не будет иметь места. Ею может быть любая линия с началом в какой-либо узловой точке).

Горизонтальные углы измерены равноточно с погрешностью m_β = 2,0″. Расстояния измерены светодальномером с погрешностью, примерно одинаковой для всех линий (m_s = 18 мм = 1,8 см). В соответствии с указанной точностью измерения расстояний и углов веса углов принимаем равными единице (p_β = 1; q_β = 1), а веса расстояний –

Координаты исходных пунктов

Исходные дирекционные углы

Измеренные горизонтальные углы и расстояния

Выполним предварительные вычисления в полигонометрических ходах (1), (2) и (3), т.е. определим координаты точек ходов, используя только измеренные величины (табл. 14.11).

Шаг 1. Общее число измерений n = 19 (11 углов и 8 расстояний), число необходимых измерений k = 10, число избыточных измерений r = 9.

Шаг 2. Составление условных уравнений.

Для трёх независимых ходов, будем иметь три условных уравнения для дирекционных углов и шесть условных уравнений для координат ( три – для абсцисс, три – для ординат).

1.

2.

3.

4.

5. (14.100)

6.

7.

8.

9.

В уравнениях (14.100) индексы (1), (2) и (3) относятся к соответствующим ходам (см. табл. 14.11), например, n₍₁₎ = 4, n₍₂₎ = 6, n₍₃₎ = 5.

Приведём условные уравнения к линейному виду по правилам, изложенным выше. В полученные выражения введём знак гауссовых сумм.

1.

2.

3.

4.

5. (14.101)

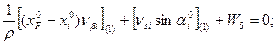
6.

7.

8.

9.

В уравнениях (14.101) значения координат берут в километрах, а значение ρ = 206265″ уменьшают на 100000.

Вычислим значения невязок в уравнениях (14.101) с учётом данных измерений и предварительных вычислений:

где T_i o – результат вычисления исходной величины T_i(исх).

W₁ = 144º 21′ 14,3″ – 144º 21′ 18,0″ = — 3,7″ ;

W₂ = 118º 19′ 09,3″ – 118º 19′ 14,7″ = — 5,4″ ;

W₃ = 118º 19′ 08,2″ – 118º 19′ 14,7″ = — 6,5″ ;

W₄ = 6124,931 – 6124,924 = +0,007 м = + 0,7 см;

W₅ = 4718,067 – 4718,048 = + 0,019 м = + 1,9 см;

W₆ = 8137,612 – 8137,565 = + 0,047м = + 4,7 см;

W₇ = 6463,765 – 6463,782 = — 0,017 м = — 1,7 см;

W₈ = 8137,580 – 8137,565 = + 0,015 м = + 1,5 см;

W₉ = 6463,752 – 6463,782 = — 0,030 м = — 3.0 см .

По данным табл. 14.11 составим табл. 14.12 значений синусов и косинусов дирекционных углов и разностей абсцисс и ординат. Получим окончательные условные уравнения поправок:

Значения синусов и косинусов дирекционных углов, значения разностей координат

Составим матрицу коэффициентов a_ij и обратных весов q_i , необходимую для определения коэффициентов нормальных уравнений коррелат (табл. 14.13).

Матрица коэффициентов и обратных весов

(продолжение табл. 14.13)

Шаг 4. Составление нормальных уравнений коррелат.

📽️ Видео

Решение системы уравнений методом обратной матрицы - bezbotvyСкачать

Лекция 8. Решение матричных уравненийСкачать

Решение систем уравнений методом подстановкиСкачать

Система линейных уравнений. Метод обратной матрицы. Матричный метод.Скачать

Метод неопределенных коэффициентовСкачать

Урок 1. Матрицы, определитель матрицы и ранг матрицы | Высшая математика | TutorOnlineСкачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Видеоурок "Уравнение прямой с угловым коэффициентом"Скачать

СУММА КОЭФФИЦИЕНТОВ: Как решать Квадратные Уравнения по МАТЕМАТИКЕ 8 классСкачать

Свойства коэффициентов квадратного уравненияСкачать

Рекуррентное вычисление определителя порядка nСкачать

Лекция 13. Исследование систем линейных уравнений. Теорема Кронекера — Капелли.Скачать

Условный экстремум и функция ЛагранжаСкачать

Приведение матрицы к ступенчатому виду. Алгоритм ГауссаСкачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

§28 Матричные уравненияСкачать

Математика без Ху!ни. Вычисление определителя методом треугольников.Скачать