Матрица коэффициентов уравнений в неявных схемах имеет (7 видео)

Матрица коэффициентов уравнений в неявных схемах имеет

Функция u(x,y) задана таблицей.

Значение частной производной , вычисленное с помощью центральной разности в точке x = 0,6; y = 1,2 равно
Функция u(x,y) задана таблицей

значение частной производной , вычисленное с помощью центральной разности, в точке x = 0,9; y = 3,2 (точка в таблице помечена галочкой) равно
Функция u(x,y) задана таблицей

Значение оператора Лапласа , вычисленное с помощью центральных разностей в точке x = 0,9; y = 2,2 равно
Функция u(x,y) задана таблицей

значение частной производной , вычисленное с помощью правой разности, в точке x = 0,5; y = 3,2 (точка в таблице помечена галочкой) равно
Функция u(x,y) задана таблицей

значение частной производной , вычисленное с помощью правой разности, в точке x = 0,5; y = 3,0 (точка в таблице помечена галочкой) равно
Функция u(x,y) задана таблицей

значение частной производной , вычисленное с помощью центральной разности, в точке x = 0,7; y = 3,2 (точка в таблице помечена галочкой) равно
Функция u(x,y) задана таблицей

значение частной производной , вычисленное с помощью центральной разности, в точке x = 0,7; y = 3,2 (точка в таблице помечена галочкой) равно ____________
Функция u(x,y) задана таблицей

значение частной производной , вычисленное с помощью левой разности, в точке x = 0,9; y = 3,2 (точка в таблице помечена галочкой) равно
Функция u(x,y) задана таблицей

Значение оператора , вычисленное с помощью центральных разностей в точке x = 0,9; y = 2,2 равно
Функция u(x,y) задана таблицей

Значение величины , вычисленное с помощью центральных разностей в точке x = 0,9; y = 2,2 равно
Функция u(x,y) задана таблицей

Значение частной производной , вычисленное с помощью центральной разности в точке x = 0,9; y = 2,2 равно
Функция u(x,y) задана таблицей

Значение величины , вычисленное с помощью центральных разностей, в точке x = 0,9; y = 2,2 равно
Функция u(x,y) задана таблицей

значение частной производной , вычисленное с помощью правой разности, в точке x = 0,6; y = 1,0 (точка в таблице помечена галочкой) равно
Функция u(x,y) задана таблицей

значение частной производной , вычисленное с помощью левой разности, в точке x = 0,6; y = 1,4 (точка в таблице помечена галочкой) равно
Функция u(x,y) задана таблицей

значение частной производной , вычисленное с помощью левой разности, в точке x = 0,7; y = 1,2 (точка в таблице помечена галочкой) равно
Функция u(x,y) задана таблицей

значение частной производной , вычисленное с помощью правой разности, в точке x = 0,5; y = 1,2 (точка в таблице помечена галочкой) равно
Функция u(x,y) задана таблицей

значение частной производной , вычисленное с помощью левой разности, в точке
x = 0,9; y = 3,2 (точка в таблице помечена галочкой) равно
Функция u(x,y) задана таблицей

значение частной производной , вычисленное с помощью левой разности, в точке x = 0,5; y = 3,4 (точка в таблице помечена галочкой) равно
Верны ли утверждения?
А) Уравнение называется волновым уравнением
B) Уравнение имеет гиперболический тип
Верны ли утверждения?
А) Уравнение описывает стационарные процессы
B) Уравнение имеет гиперболический тип
Верны ли утверждения?
А) Уравнение Лапласа имеет параболический тип
B) Уравнение Лапласа имеет одну пространственную переменную
Верны ли утверждения?
А) Уравнение Лапласа описывает нестационарные процессы
В) Уравнение Лапласа имеет параболический тип
Верны ли утверждения?
А) Уравнение Лапласа описывает стационарные процессы
B) Уравнение Лапласа имеет гиперболический тип
Верны ли утверждения?
А) Уравнение Лапласа описывает стационарные процессы
B) Уравнение Лапласа имеет в правой части нуль
Верны ли утверждения?
А) Уравнение Пуассона описывает стационарные процессы
B) Уравнение Пуассона имеет ненулевую правую часть
Верны ли утверждения?
А) Уравнение Пуассона описывает стационарные процессы
B) Уравнение Пуассона имеет эллиптический тип
Для интегральных уравнений
А) однородное уравнение Фредгольма второго рода всегда имеет нулевое решение
B) ненулевые решения однородного уравнения Фредгольма существуют только для некоторых значений параметра
Для интегральных уравнений
А) Ядро является вырожденным
B) Ядро является вырожденным
Для интегральных уравнений
А) Ядро является вырожденным
B) Ядро является вырожденным
Для интегральных уравнений Фредгольма второго рода
A) ненулевые решения однородного уравнения называют собственными функциями
B) значения величины , при котором существуют ненулевые решения уравнения называют собственными значениями
Для интегральных уравнений Фредгольма второго рода
A) однородное уравнения всегда имеет нулевое решение
B) ненулевое решение существует при любом значении величины
Для интегральных уравнений Фредгольма справедливы ли следующие утверждения?
А) все собственные значения симметричного ядра – действительные числа
B) собственные функции симметричного ядра ортогональны
Для интегральных уравнений Фредгольма справедливы ли следующие утверждения?
А) симетричное ядро имеет хотя бы одно собственное значение
B) собственные функции симметричного ядра не могут быть ортогональны
Для интегральных уравнений
A) ненулевые решения однородного уравнения Фредгольма второго рода существуют для любых значений параметра
B) ненулевые решения однородного уравнения Фредгольма существуют только для некоторых значений параметра
Для уравнений в частных производных могут быть использованы следующие численные методы решения:
А) вариационные
В) конечно-разностные
Для уравнений в частных производных могут быть использованы следующие численные методы решения:
А) метод Симпсона
В) метод Гаусса
Для уравнений в частных производных могут быть использованы следующие численные методы решения:
А) прямые
В) одношаговые
Задача решения дифференциального уравнения с дополнительными условиями

называется
Задача решения дифференциального уравнения с дополнительными условиями

называется
Неустойчивость разностной схемы может быть
А) условной
В) безусловной
Постановка задачи для уравнения в частных производных включает в себя:
A) условия неединственности решения задачи
В) область решения задачи
Постановка задачи для уравнения в частных производных включает в себя:
А) вид уравнения
В) дополнительные условия, обеспечивающие единственность решения задачи
Постановка задачи для уравнения в частных производных включает в себя
А) вид уравнения
В) область решения задачи
Система линейных уравнений для разностной схемы с использованием центральных разностей для задачи

является
Существуют следующие методы решения интегральных уравнений:
А) метод последовательных приближений
В) квадратурные методы
Тип уравнения в частных производных второго порядка
определяется следующим:
Уравнение в частных производных

А) имеет второй порядок
В) является линейным для любых функций, задающих коэффициенты уравнения
Уравнение в частных производных второго порядка

А) имеет параболический тип, если
В) имеет гиперболический тип, если
Уравнение в частных производных второго порядка

A) имеет эллиптический тип, если
В) имеет гиперболический тип, если
Уравнение в частных производных второго порядка
называется эволюционным, если
Устойчивость разностной схемы может быть
А) безусловной
В) характерной
Формулы для аппроксимации первой производной конечными разностями имеют вид:
А) для правой разности
В) для левой разности
Формулы для аппроксимации первой производной конечными разностями имеют вид:
А) для центральной разности
В) для правой разности
Аппроксимация разностной схемы для уравнений в частных производных характеризует
Величина, характеризующая отклонение приближенного значения производной от ее истинного значения, — это
Волновое уравнение имеет тип
Для интегрального уравнения функция называется
Если для ядра интегрального уравнения выполняется условие , то ядро называется
Задача, которая состоит в решении уравнения с частными производными при заданных начальных условиях, если задача решается в неограниченном пространстве и граничные условия не заданы, называется задачей
Интегральное уравнение является
Конечно-разностный метод сводит решение краевой задачи для обыкновенного дифференциального уравнения к более простой задаче
Краевую задачу для уравнения Лапласа называют задачей Дирихле, если граничные условия имеют вид
Матрица коэффициентов в конечно-разностной схеме решения уравнения Лапласа при использовании центральных разностей является
Нестационарные задачи для уравнений в частных производных, решаемые в ограниченной пространственной области, при формулировке которых ставятся и начальные, и граничные условия, называются
Неявная разностная схема аппроксимирует уравнение теплопроводности со следующим порядком по пространству и времени —
Неявная схема для одномерного нестационарного уравнения теплопроводности является
Неявная схема для уравнения одномерной нестационарной теплопроводности имеет вид
Показатель степени k в формуле, определяющей зависимость погрешности аппроксимации производной от шага таблицы в виде называется
Порядок погрешности аппроксимации формулы равен
Порядок погрешности аппроксимации формулы равен
Порядок погрешности аппроксимации формулы равен
Порядок погрешности аппроксимации формулы равен
Разностная схема аппроксимирует исходную дифференциальную задачу, если
Уравнение называется уравнением
Уравнение является
Уравнение в частных производных называется квазилинейным, если коэффициенты уравнения
Уравнение Лапласа имеет вид
Уравнение нестационарной теплопроводности имеет тип
Уравнение нестационарной теплопроводности является
Уравнение переноса имеет вид
Уравнение переноса имеет вид
Уравнение Пуассона имеет вид
Условие устойчивости явной разностной схемы для одномерного нестационарного уравнения теплопроводности имеет вид
Устойчивость разностной схемы для уравнений в частных производных характеризует
Формула для аппроксимации второй производной центральной разностью имеет вид:
Шаблон разностной схемы показывает
Явная разностная схема аппроксимирует уравнение теплопроводности со следующим порядком по пространству и времени
Ядро интегрального уравнение, имеющее вид , называется
Ядро интегрального уравнения называется вырожденным, если оно имеет вид
Ядро интегрального уравнения, имеющее вид называется
Гиперболическое волновое уравнение имеет вид
Интегральным называется уравнение,
Одномерное нестационарное уравнение теплопроводности имеет вид
Разностная схема называется устойчивой, если
Решение уравнения в частных производных называется нестационарным, если решение

Видео:Решение системы уравнений методом ГауссаСкачать

Методы явные и неявные

Дата добавления: 2015-06-12 ; просмотров: 15083 ; Нарушение авторских прав

Процесс формирования математической модели для численного интегрирования обязательно включает этап алгебраизации, который состоит в преобразовании обыкновенных дифференциальных уравнений в алгебраические. Он основан на использовании одного из методов численного интегрирования.

Если задано дифференциальное уравнение

(3.1)

и начальные условия , то очередное значение может быть получено интегрированием (3.1):

(3.2)

Определенный интеграл в (3.2) численно равен площади под кривой на интервале (рис. 3.2).

Приближенно эта площадь может быть вычислена как площадь прямоугольника, высота которого равна значению функции на левой границе интервала или значению на правой границе интервала. Очевидно, площади обоих прямоугольников, ограниченных сверху отрезками 1 и 2 на рис. 3.3, будут тем ближе к точному значению интеграла, чем меньше шаг интегрирования .

Подставив в (3.2) приближенные значения интеграла, можно получить две формулы:

(3.3)

. (3.4)

Выражение (3.3) представляет собой формулу явного метода Эйлера. Называется метод явным потому, что неизвестное значение 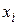может быть непосредственно вычислено по известному значению в предыдущей точке.

Формула (3.4) соответствует неявному методу Эйлера. Здесь в правой части выражения используется неизвестное значение 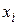, поэтому вычислить его непосредственно по этой формуле нельзя.

Более точное значение интеграла (3.2) дает метод трапеций, которому соответствует отрезок 3 на рис. 3.3. Тогда

. (3.5)

Эта формула относится, очевидно, тоже к неявным.

Для явных методов процедура формирования модели для численного интегрирования ограничивается алгебраизацией исходных дифференциальных уравнений. В частности, формула (3.3) не требует дальнейших преобразований и готова для применения.

Для неявных методов дальнейшие действия зависят от того, какой метод решения системы нелинейных уравнений реализован в данном пакете. Одним из вариантов может быть использование итерационного метода Ньютона, который, как известно, обладает наибольшей скоростью сходимости среди практически применяемых методов, и в котором многократно решается система линеаризованных алгебраических уравнений.

В этом случае реализуется второй этап подготовки математических моделей для неявных методов, который состоит в линеаризации нелинейных алгебраических уравнений, т.е. в разложении нелинейных функций в ряд Тэйлора и сохранении в результате только линейных членов.

Пусть задано нелинейное алгебраическое уравнение

(3.6)

где – вектор переменных.

Разложение (3.6) в ряд Тэйлора с сохранением только линейных членов дает приближенную замену

(3.7)

где –начальное приближение, в качестве которого берутся значения переменных на предыдущем шаге интегрирования;

– неизвестное значение переменной на шаге интегрирования.

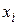
Выражение (3.7) может быть записано как линейное алгебраическое уравнение

,(3.8)

где – вычисляется для известных значений переменных на предыдущем шаге интегрирования;

Таким образом, процесс численного моделирования в общем случае нелинейных систем неявными методами состоит в формировании и решении на каждом шаге интегрирования системы линейных алгебраических уравнений

, (3.9)

которая включает компонентные и топологические уравнения моделируемой схемы. При этом, процедурам алгебраизации и линеаризации подвергаются только компонентные уравнения, так как топологические уравнения всегда линейные алгебраические.

Рассмотрим пример связанный с подготовкой модели для численного решения нелинейного дифференциального уравнения второго порядка

Первым шагом является сведение данного уравнения к задаче Коши, т.е. к системе уравнений первого порядка за счет введения новой переменной :

Явные формулы метода Эйлера имеют вид

Неявные формулы запишутся следующим образом:

Для перехода к матричной записи выполним ряд преобразований:

Здесь ,

Матричная запись имеет вид

Формулу (3.7), вообще говоря, необходимо применять итерационно. Решение этого уравнения, найденное для заданного начального приближения , следует использовать в качестве очередного приближения в (3.7) и повторять формирование и решение линейного алгебраического уравнения до тех пор, пока два последовательных приближения не станут близкими с заданной точностью. При численном моделировании можно ограничиться только одной итерацией, выбирая достаточно малый шаг интегрирования и учитывая, что при этом значения переменных на предыдущем шаге являются достаточно хорошим приближением.

3.2.3. Выбор между явными и неявными методами
в процедурах моделирования технических систем

Выбор между явными и неявными методами представляет серьезную проблему. Многие специалисты считают неявные методы более мощным и универсальным инструментом для решения задач моделирования технических систем [23, 15]. Следует, однако, заметить, что лишь недавно появились достаточно мощные и универсальные системы автоматизированного моделирования, такие, как, например, MATLAB или МВТУ [17], допускающие выбор явного или неявного метода решения задачи. Раньше использовались либо явные, либо неявные методы, так как это требовало разных компонентных моделей.

В современных перспективных системах автоматизированного моделирования, пригодных для моделирования технических систем, применяются, как правило, неявные методы численного интегрирования. Неявные методы лучше приспособлены для решения систем дифференциальных и алгебраических уравнений, к тому же они более устойчивы. В результате, несмотря на большие затраты машинного времени на каждом шаге интегрирования, связанные с необходимостью решения СЛАУ, общие затраты могут быть значительно меньше за счет увеличения шага интегрирования и уменьшения общего количества шагов.

Рассмотрим эту особенность неявных методов на примере явного и неявного методов Эйлера [21], определяемых формулами (3.3) и (3.4), соответственно.

Применим указанные формулы для численного интегрирования простейшего линейного дифференциального уравнения

Характеристическое уравнение данной динамической системы имеет вид

, или ,

где – постоянная времени системы.

Единственный полюс системы находится в левой полуплоскости, следовательно, исходная система устойчива. Соответственно, любое решение уравнения, при , стремится к нулю.

Разностное уравнение, соответствующее численному решению явным методом Эйлера, запишется как

Известно, что условием устойчивости полученного разностного уравнения является

или .

Это означает, что выбор может качественно изменить вид решения, превратив устойчивый процесс в неустойчивый.

Таким образом, на шаг интегрирования наложено очевидное ограничение – он не может быть больше постоянной времени системы, иначе дискретная аппроксимация станет неустойчивой. Если система имеет несколько постоянных времени, то подобное ограничение связывает шаг интегрирования с самой маленькой постоянной времени.

Переход к методам более высокого порядка мало меняет картину. Для метода Рунге – Кутты 4-го порядка требование устойчивости ограничивает шаг величиной , или, в более общем виде, , где – максимальное собственное значение матрицы Якоби [29].

Применение неявного метода Эйлера к той же системе дает

где ограничение на величину шага выглядит по-другому:

что позволяет выбрать шаг любой величины, ориентируясь только на требуемый уровень погрешности.

Видео:Матричный метод решения систем уравненийСкачать

Явная и неявная схемы решения

Особенностью нестационарной задачи является необходимость последовательного прослеживания промежуточных предыдущих состояний тела для правильного расчета текущего состояния, т. е. рассмотрение истории процесса, в то время как для стационарного процесса понятие истории не существует, так как каждое состояние может быть рассчитано независимо от предыдущих.

Если историю процесса прослеживать с достаточно мелким шагом по времени, то можно пренебречь влиянием на температуру данной точки тела температур удаленных от нее точек, т. е. считать, что на каждом шаге порция тепла пересекает только одну границу — между двумя соседними ячейками. Можно также, определив мощности тепловых потоков через границы ячейки на момент начала шага, считать их в течение шага постоянными. В этом случае система уравнений для расчета температур в конце шага оказывается очень простой и распадается на отдельные уравнения, в каждом из которых есть только одно неизвестное. Такая схема решения называется явной и требует существенно меньшего объема вычислений по сравнению с неявной схемой, в каждом уравнении которой присутствует несколько неизвестных.

На рис. 13.9 решение по явной схеме (1м) представлено ломаной линией, каждый отрезок которой соответствует шагу решения. Если в начале шага правильно определено направление отрезка (он параллелен касательной к кривой искомой функции), то эта ломаная с определенной точностью повторяет вид кривой T(t).

Но если при этом шаг решения недостаточно мелкий, то предположение о сохранении постоянства тепловых потоков становится некорректным и приводит к неправильному решению (ломаная

Рис. 13.9. Результаты расчета изменения температуры T(t) по явной (7) и неявной (2) схемам решения при малом (м) и большом (6) шаге

16 удаляется от кривой T(t)). Максимально допустимый шаг по времени т прямо пропорционален квадрату линейного размера самого мелкого элемента / и зависит от свойств материала (для тепловой задачи он обратно пропорционален коэффициенту температуропроводности а), т. е.

Поэтому при решении стационарных задач, как правило, выгоднее один раз составить и решить систему уравнений неявной схемы, чем выполнять большое число шагов, необходимое для решения по явной схеме. Решение по неявной схеме (2м, 26) представлено на рис. 13.9 ломаной, составленной из секущих, начало и конец которых лежат на кривой T(t). Порядок точности явной и неявной схем (отклонение ломаной от кривой) при одинаковом мелком шаге одинаков (1м и 2м). При увеличении шага решение по неявной схеме, хотя и становится грубее, но остается устойчивым (ломаная 26 продолжает следовать за кривой T(t)). Если функция меняется медленно, то погрешность при этом невелика. Таким образом, явная схема эффективнее для нестационарных задач (переходных процессов), где большое число шагов неизбежно, а неявная — для стационарных задач.

Взаимные связи процессов, протекающих при сварке и эксплуатации конструкции (см. рис. 13.1), в некоторых случаях не мешают моделировать процессы последовательно, на отдельных моделях. Например, если протекание тока вызывает нагрев, а нагрев — структурные и фазовые превращения и деформации от теплового расширения, то можно сначала провести моделирование процесса протекания тока, затем рассмотреть процесс распространения теплоты и т. д. Связи между процессами будут учтены, если результаты, полученные с использованием каждой модели, войдут в начальные и граничные условия и повлияют на свойства материала, учитываемые в следующих за ней моделях. Такая последовательно решаемая задача называется несвязной. При ее решении пренебрегают обратными связями между процессами (на рис. 13.1 они показаны стрелками, направленными к процессу с меньшим номером): влиянием нагрева на протекание тока, разогревом от пластической деформации и т. д. Это существенно упрощает разработку программ и сокращает затраты ресурсов компьютера при выполнении программ, однако существуют задачи, для которых такой метод решения неприменим.

Примером задачи, которую необходимо решать как связную, является моделирование контактной сварки. Площадь и плотность контакта, через который протекает ток, существенно зависят от силы сжатия и деформации свариваемых деталей. В свою очередь, деформации зависят от изменения предела текучести и плавления металла при его нагреве проходящим током. Следовательно, все процессы необходимо моделировать в рамках единой связной задачи.

Связная задача требует составления общей системы уравнений для нескольких взаимосвязанных процессов. Такой подход является правильным, но существенно более сложным для реализации моделирования. Выбор связной или несвязной задачи при моделировании должен быть сделан на основе оценки погрешности, устранение которой обеспечивается учетом обратных связей между процессами.

Достаточно полноценную замену связного моделирования можно обеспечить при итерационном решении на несвязной модели, если моделировать процессы поочередно, но повторить решение несколько раз, вводя поправки в каждую модель с учетом результатов, полученных на остальных моделях при предыдущей итерации.

Рис. 13.10. Блок-схема программы связного моделирования процессов протекания тока, нагрева, структурных превращений и диффузии водорода при сварке

Сходимость итерационного процесса, как и при решении нелинейных задач, зависит от степени влияния обратных связей на результаты решения. Блок-схема такой программы показана на рис. 13.10.

Еще более простой алгоритм можно использовать при решении задачи по явной схеме с малыми шагами по времени. В этом случае нет необходимости в итерациях на каждом шаге. Обратные связи между процессами будут учтены, хотя и с запаздыванием на один шаг. При достаточно малом шаге будет получен результат, близкий к результату решения связной задачи.