Общее решение этого уравнения можно получить только в некоторых частных случаях.
Видео:Решение матричных уравненийСкачать

Решение дифференциального уравнения Риккати при известном частном решении
Рассмотрим дифференциальное уравнение Риккати:
(1) .
Пусть известно его частное решение :
Тогда подстановкой уравнение Риккати (1) приводится к уравнению Бернулли:
;
;
;
;
.
Это уравнение Бернулли с n = 2 .
Видео:Матричные уравнения Полный разбор трех типов матричных уравненийСкачать

Свойства уравнения Риккати
Не меняет вид уравнения:
- Произвольное преобразование независимого переменного:
- Произвольное дробно-линейное преобразование зависимого переменного:
При таких подстановках уравнение также является уравнением Риккати, но с другими функциями p, q, r.
Вид общего решения
Общее решение уравнения Риккати есть дробно-линейная функция от произвольной постоянной:
И наоборот если общее решение уравнения есть дробно-линейная функция от произвольной постоянной, то соответствующее уравнение есть уравнение Риккати.
Видео:§29 Решение матричного уравненияСкачать

Упрощение уравнения Риккати
Снова рассмотрим дифференциальное уравнение Риккати:
(1) .
Подстановкой
,
где А – постоянная, оно приводится к виду:
(2) ,
где .
Далее, подстановкой
оно приводится к виду:
(3)
где .
Видео:Матричный метод решения систем уравненийСкачать

Упрощенное уравнение Риккати
Упрощенное уравнение Риккати – это уравнение вида:
(4) ,
где A, B – постоянные. Оно интегрируется при
,
где – целое.
Покажем это. Сделаем подстановку:
;
.
Подставляем в (4):
.
Умножаем на :
(5) .
Но
.
Подставляем в (5):
Или
(6)
где
.
Уравнение (6) интегрируется при
.
Для этого разделим его на и перепишем в следующем виде:
;
;
.
Это уравнение с разделяющимися переменными. Оно легко интегрируется.
При уравнение (6) можно преобразовать двумя путями.
- Подстановкой , где , оно преобразуется к виду: .
- Подстановкой , где , оно преобразуется к виду:
Таким образом, при , где n — целое число, ряд подстановок приводит к полному решению.
Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.
Автор: Олег Одинцов . Опубликовано: 14-08-2012
Видео:§28 Матричные уравненияСкачать

Матричное уравнение риккати как решить
РАБОТА 2. РЕШЕНИЕ МАТРИЧНОГО УРАВНЕНИЯ РИККАТИ
Задание. Научиться решать нелинейные квадратичные матричные уравнения сведением их к полной проблеме собственных значений.
Внимание. Согласно приказам по Высшей школе, 20% ВКР 2022 г. бакалавров и магистров должны быть в форме Start-up’-ов. Методичка построена таким образом, что ВСЕ алгоритмы, которые вам нужны для отчета, даны. Копируйте к себе в отчет, как есть. Покажите себя в кратком, емком комментарии. Считайте, что вы статью пишете. Это стандартное введение ко всем работам о распространенных ошибках. Никому не нужен тарабарский отчет, состоящий в ASCII кодах методички, когда степени падают и становятся коэффициентами. Ну вот вас направь проверять ваши группы. Поставьте себя на место того, кому вы отчет пишете. Как вам 40 штук работ в стиле копипаста? Если вы пишете свой комментарий, даже без формул, они у вас отличаться начнут. Пример текста отчета.
Ниже дан пример решения P нелинейного квадратичного уравнения PRP+PA+A’P+Q=0. Уравнения такие возникли впервые в работах математика Риккати. В матричной форме уравнение сводится к уравнению, отличного от линейного Ax=b. Метод Гаусса к Ax=λx не применим. Возможно разделение с выделением полиномиального уравнения для λ. Оказывается, что решение серии таких уравнений с фиксированными λ, отличающимися отрицательными вещественными частями, дает в итоге желаемое: решение нелинейного уравнения. Тем самым, квадратичные уравнения хотя и сложны, но разрешимы сведением их к проблеме собственных значений.
ФАКУЛЬТАТИВ ПО ЧИСЛЕННЫМ МЕТОДАМ
Необязательная часть методички, связанная с расширительными пояснительными примерами и формулами. Переносить их в отчет не надо. Ныне это классический хорошо известный метод.
Уравнение Ax=B описывает то, во сколько раз A «усиливается» воздействие x, проходя на выход B. По сути, это обобщенное уравнение рычага.
Уравнение Mx=λx описывает резонанс: явление, не присущее рычагу, но хорошо известное у динамических систем. Оно описывает резонансные сигналы x, проходящие через систему M без изменений, усиливаясь в λ раз.
Поэтому свести эти две знаменитые задачи, рычаг к динамической системе, и динамическую систему к рычагу, не удается. Тем не менее, экстремум квадратичной функции x 2 ищется в точке равенства нулю ее производной 2x=0, а это уже линейное уравнение.
Исторические сведения. РИККАТИ Якопо Франческо – итальянский математик рубежа XVIII века. Учился в Падуе. С 1747 жил в Венеции. Известен также инженерной деятельностью, он руководил постройкой речных плотин. Основные труды относятся к интегральному исчислению и дифференциальным уравнениям. Автор исследований об интегрируемости в элементарных функциях одного типа дифференциального уравнения 1-го порядка, названного его именем. Отмеченное уравнение описывает стационарную точку решения.
Разумеется, этот ученый в силу давности лет никакого матричного уравнения не решал. Уравнение названо в честь его потому, что Риккати ввел в рассмотрение помимо линейного дифференциального уравнения ∂p/∂t=a(t)p квадратичное обобщение ∂p/∂t=2a(t)p±r(t)p 2 +q(t). Такие уравнения описывают решение, как функцию времени. В точке равновесия например, это нижнее положение) движения не наблюдается ∂p/∂t=0.
В стационарных условиях, когда дифференциальное уравнение, рассматривавшееся им, вырождается в стационарное, возникает специфичное условие. Если функция не меняется (производная равна 0), будучи константой, появляется полиномиальное уравнение (решения – корни полинома). Если P – матрица, этот случай и рассмотрен при стационарных коэффициентах, теперь уже, матриц A, R, Q. Оно оказалось ключевым для поиска коэффициентов регуляторов, кроме того, мы научились его решать.
Матричное уравнение Риккати. При известных A, R, Q (A 0, матрицы R и Q симметричны), рассматривается квадратичное уравнение для P вида
Нотациями A 0 принято обозначать знаки реальной части собственных значений матриц, они не могут быть произвольными (собственные значения в матричных пакетах дает функция eig). Собственные значения матрицы A, следовательно, лежат в левой части комплексной плоскости, а у матрицы Q – в левой.
Существуют всего две крупные задачи линейной алгебры: решение задачи Ax=B и решение сходной проблемы собственных значений Mx=λx (в матричной форме MX=XΛ, где Λ=diag(λ1,λ2. λn) – диагональная матрица собственных значений – спектр матрицы M, размещаемый на диагонали Λ, X – матрица собственных векторов x). Если ищутся и собственные значения λ и собственные векторы x, то проблема называется полной.
Алгоритмы решения этих двух задач составляют ядро численных пакетов линейной алгебры. Вторая задача звучит как сведение M к диагональной матрице Λ=X –1 MX. Разумеется, не всякая матрица может быть диагонализована, ровно также, как метод Гаусса не может все возможные матрицы свести к треугольным. Диагонализация – более время-затратная операция, дающая составляющие Λ и X. Для M=[A R, –Q –A’] через них выражается решение квадратичного матричного уравнения Риккати.
Алгоритм решения P=WV –1 связан с расчетом для M усеченной матрицы ее собственных векторов X=(H|*), где H=[V; W] содержит верхний V и нижний W блоки, отвечающие отрицательным и положительным реальным частям комплексных собственных значений спектра Λ.
Немаловажно то, что уравнение Риккати квадратично. Выходит, что квадратичная задача оптимизации порождает линейную задачу, это отвечает фазе нахождения собственных векторов после установления собственных значений.
Отметим кратко, что уравнение Mx=λx нелинейно, поскольку содержит произведение неизвестных в правой части. Алгоритм Гаусса тут не применим, но его можно употребить вполне формально к преобразованной системе (M–λI)x=0, I=diag(1,1. 1). Тривиальное нулевое решение x=(M–λI) –1 0 существует, но оно нам не интересно. Не тривиальное возможно только тогда, когда инвертируемая матрица M–λI не имеет обратной: det(M–λI)=0.
Уравнение det(M–λI)=0 называется характеристическим уравнением матрицы. Оно полиномиально, это полином от λ. После того, как произошло отделение мух λ1, λ2, . от котлет x, решить линейное теперь уже матричное уравнение (M–λI)x=0 (при подстановке значений λ) относительно матрицы X всех собственных векторов несложно.
Деление матрицы собственных векторов X=(H|*) на две части (пополам) тоже имеет хорошо известную вам физическую интерпретацию.
Механические системы не изобретательны, шарик скатывается с горы по минимальной траектории (оптимально), катясь вниз. Его продолжение, качели, заняты перекачкой потенциальной энергии взмаха в кинетическую энергию прохождения нижнего положения. Электромагнитная волна связана с перекачкой энергии в электрическую и магнитную составляющие. Эти составляющие сопряжены друг с другом.
Электричество и магнетизм – хорошо известные нам явления природы. Когда мы заняты конструированием оптимального регулятора, последний выступает как сопряженная к системе часть. У оптимальных динамических систем действие объекта на регулятор сопровождается возвратом по цепи обратной связи циркулирующего в кольце возбуждения.
Такая сцепка двух похожих систем обязана приводить к квадратичной задаче, что мы и наблюдаем. Так как система динамическая, неизбежно появляется спектр собственных значений Λ, описывающий ее резонансы, и собственные векторы X. Причем спектр распадается на горизонтально сопряженные (симметричные относительно вертикальной оси комплексной плоскости) числа.
Отсюда родом P=WV –1 , выражающая решение ровно через половину матрицы собственных векторов X=(H|*), где прямоугольник H=[V; W] разбит на квадратные блоки. Вторая половинка собственных векторов в расчет не идет, у оптимальных систем она не произвольная, а «сопряженная» ровно также, как сопрягаются электричество и магнетизм.
Всего этого Якопо, разумеется, не знал и не мог знать. Собственные числа и собственные векторы, изобретенные математиками для матриц, были переоткрыты в начале прошлого века физиками. Например, Гейзенбергом при изучении таблиц, связанных с исследованиями резонансных явлений у атомов.
Компьютеры открыли путь к решению характеристического уравнения матрицы, так что тематика, которую вы изучаете, очень молода, и связана со свойствами, присущими к экономной природе, которая лишнего не имеет, но и своего не отдаст.
Видео:Лекция 8. Решение матричных уравненийСкачать

Дифференциальное уравнение Риккати
Дифференциальное уравнение первого порядка вида
где — известные функции, называется уравнением Риккати (обобщенным). Если коэффициенты в уравнении Риккати постоянны, то уравнение допускает разделение переменных, и мы сразу получаем общий интеграл
Как показал Лиувилль, уравнение (1) в общем случае не интегрируется в квадратурах.
Свойства уравнения Риккати
1. Если известно какое-нибудь частное решение уравнения (1), то его общее решение может быть получено при помощи квадратур.
В самом деле, положим
где — новая неизвестная функция. Подставляя (2) в (1), найдем
откуда, в силу того что есть решение уравнения (1) получим
Уравнение (3) является частным случаем уравнения Бернулли.
Пример 1. Решить уравнение Риккати
зная его частное решение .
Решение. Положим и подставим в уравнение (4); получим
Таким образом, общее решение уравнения (4) .
Замечание. Вместо подстановки (2) часто бывает практически более выгодной подстановка
которая сразу приводит уравнение Риккати (1) к линейному .
2. Если известны два частных решения уравнения (1), то его общий интеграл находится одной квадратурой.
Пусть известны два частных решения и уравнения (1). Используя тот факт, что имеет место тождество
представим уравнение (1) в виде
Для второго частного решения аналогично находим
Вычитая из равенства (5) равенство (6), получаем
Пример 2. Уравнение имеет частные решения . Найти его общий интеграл.
Решение. Используя формулу (7), получаем общий интеграл исходного уравнения
📽️ Видео
Матричное уравнениеСкачать

Решить матричное уравнениеСкачать

Стабилизация линейной системы с постоянными коэффициентами и алгебраическое уравнение РиккатиСкачать

Решение уравнения РиккатиСкачать

Матричные уравненияСкачать

Решение системы уравнений методом обратной матрицы - bezbotvyСкачать

Простейшее матричное уравнениеСкачать

Матричные уравненияСкачать

Об одном подходе к синтезу нелинейного управления на основе матричного уравнения РиккатиСкачать

Матричные уравнения. ТемаСкачать

Решение системы уравнений методом Крамера.Скачать

Линейная алгебра, 7 урок, СЛАУ. Матричный методСкачать

22. Матричные уравненияСкачать

Решение матричного уравнения X(2 3 2; 1 2 −3; 3 4 1) = (1 0 3; 4 1 4; 2 −1 3) Высшая математика.Скачать

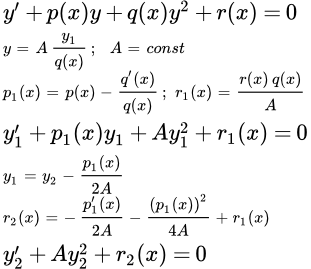
.jpg)