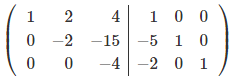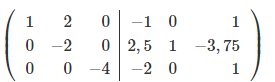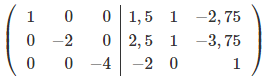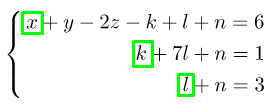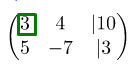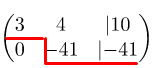Матричное уравнение методом элементарных преобразований

Для того что бы найти обратную матрицу можно использовать два метода: с помощью алгебраических дополнений (метод присоединённой (союзной) матрицы) или элементарных преобразований (метод Жордано-Гаусса). Рассмотрим как найти обратную матрицу с помощью элементарных преобразований.

Обратной матрицей называется матрицы A -1 при умножении на исходную матрицу A получается единичная матрица E.

Алгоритм нахождения обратной матрицы с помощью элементарных преобразований:

1. Найти определитель (детерминант) матрицы A. Если определитель ≠ 0, то обратная матрица существует. Если определитель = 0, то обратная матрица не существует.
2. Дописываем справа единичную матрицу
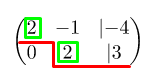
3. Делаем прямой ход. Обнуляем все элементы (с помощью элементарных преобразований) левой матрицы стоящей под ее главной диагонали.
4. Делаем обратный ход. Обнуляем все элементы (с помощью элементарных преобразований) левой матрицы стоящей над ее главной диагонали.
5. Элементы главной диагонали левой матрицы, преобразуем в единицы.

Видео:Решение матричных уравненийСкачать

Пример

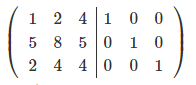
Рассмотрим данный метод на примере. Дана матрицы 3х3:

Допишем к нашей матрице слева единичную матрицу.

Чтобы сделать нули под элементом a₁₁, вычтем 1-ую строку из всех строк, что расположены ниже её, при чём, для того, чтобы работать с меньшими числами, поделим каждую из этих строк на a₁₁.

Чтобы сделать нули над элементом a₃₃, вычтем 3-ую строку с всех строк, что расположены выше её, при чём, для того, чтобы работать с меньшими числами, поделим каждую из этих строк на a₃₃.

Чтобы сделать нули над элементом a₂₂, вычтем 2-ую строку с всех строк, что расположены выше её, при чём, для того, чтобы работать с меньшими числами, поделим каждую из этих строк на a₂₂.

Поделим каждую строку на элемент, который стоит на главной диагонали.

Видео:Элементарные преобразования матриц. Высшая математика.Скачать

Метод элементарных преобразований (методы Гаусса и Гаусса-Жордана для нахождения обратных матриц).

В первой части был рассмотрен способ нахождения обратной матрицы с помощью алгебраических дополнений. Здесь же мы опишем иной метод нахождения обратных матриц: с использованием элементарных преобразований.

Пусть нам задана квадратная матрица $A_<ntimes>$. Допишем справа к матрице $A$ единичную матрицу $E$ n-го порядка. После такого дописывания мы получим матрицу $left(A|Eright)$. Со строками этой матрицы можно выполнять такие преобразования:

1. Смена мест двух строк.
2. Умножение всех элементов строки на некоторое число, не равное нулю.
3. Прибавление к элементам одной строки соответствующих элементов другой строки, умноженных на любой множитель.

Конечная цель указанных выше преобразований: привести матрицу $left(A|Eright)$ к такому виду: $left(E|A^right)$. Т.е. нужно сделать так, чтобы матрица до черты стала единичной, тогда после черты будет записана обратная матрица $A^$.

Добиться этой цели можно, выполняя над исходной матрицей $left(A|Eright)$ преобразования метода Гаусса или Гаусса-Жордана. Перед тем, как перейти к описанию этих методов, оговорим, что изначально матрица $A_<ntimes>$ не должна иметь нулевых строк или столбцов. Если в матрице $A$ есть хоть один нулевой столбец или нулевая строка, то обратная матрица $A^$ не существует.

Строки матрицы станем обозначать буквами $r$ (от слова «row»): $r_1$ – первая строка, $r_2$ – вторая строка и так далее.

Видео:Нахождение обратной матрицы с помощью элементарных преобразованийСкачать

Метод Гаусса

Этот метод делят на два этапа, которые называют прямым ходом и обратным.

Видео:Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Прямой ход метода Гаусса

В процессе выполнения прямого хода мы последовательно используем строки матрицы. На первом шаге работаем с первой строкой, на втором шаге – со второй и так далее. Если в ходе решения в матрице до черты возникла нулевая строка, то прекращаем преобразования, так как обратная матрица $A^$ не существует.

На первом шаге прямого хода обратимся к первой строке $r_1$. Если первый элемент $a_1$ первой строки не равен нулю, то выполняем обнуление всех ненулевых элементов первого столбца, лежащих под первой строкой. Если же $a_1=0$, то меняем местами первую строку с одной из тех нижележащих строк, у которых первый элемент отличен от нуля, а затем уже производим обнуление.

На втором шаге прямого хода обратимся к второй строке $r_2$. Если второй элемент $a_2$ второй строки не равен нулю, то выполняем обнуление всех ненулевых элементов второго столбца, лежащих под второй строкой. Если же $a_2=0$, то меняем местами вторую строку с одной из тех нижележащих строк, у которых второй элемент отличен от нуля, а затем уже производим обнуление. В случае, когда второй элемент равен нулю как у второй строки, так и у всех нижележащих строк, прекращаем решение, так как обратная матрица $A^$ не существует.

Полагаю, логика прямого хода ясна. На некоем k-м шаге мы работаем с строкой $r_k$. Если k-й элемент $a_k$ этой строки не равен нулю, то выполняем обнуление всех ненулевых элементов k-го столбца, лежащих под строкой $r_k$. Если же $a_k=0$, то меняем местами строку $r_k$ с одной из тех нижележащих строк, у которых k-й элемент отличен от нуля, а затем уже производим обнуление. В случае, когда k-й элемент равен нулю как у строки $r_k$, так и у всех нижележащих строк, прекращаем решение, так как обратная матрица $A^$ не существует.

Когда мы придём к последней строке, матрица до черты станет верхней треугольной, т.е. все элементы под главной диагональю будут равны нулю. Это будет означать конец прямого хода метода Гаусса.

Видео:Матричный метод решения систем уравненийСкачать

Обратный ход метода Гаусса

На этом этапе мы поднимаемся по матрице «снизу вверх». Сначала используем последнюю строку $r_n$, затем предпоследнюю $r_$ и так далее, пока не дойдём до первой строки. С каждой строкой выполняем однотипные операции.

Пусть, например, речь идёт о некоей k-й строке. Матрица, расположенная до черты, содержит в строке $r_k$ диагональный элемент $a_$. Если $a_=1$, то это нас вполне устраивает, а если $a_neq$, то просто умножаем строку $r_k$ на коэффициент $frac<a_>$, чтобы диагональный элемент стал равен 1. Затем с помощью строки $r_k$ обнуляем элементы k-го столбца, расположенные над строкой $r_k$.

Как только мы дойдём до первой строки, матрица до черты станет единичной, и алгоритм завершится.

Видео:Решение системы уравнений методом ГауссаСкачать

Метод Гаусса-Жордана

Последовательно используем строки матрицы. На первом шаге работаем с первой строкой, на втором шаге – со второй и так далее. Если в ходе решения в матрице до черты возникла нулевая строка, то прекращаем преобразования, так как обратная матрица $A^$ не существует.

На первом шаге прямого хода обратимся к первой строке $r_1$. Первый элемент этой строки обозначим как $a_1$. Если $a_1=0$, то меняем местами первую строку с одной из тех нижележащих строк, у которых первый элемент отличен от нуля. Затем, если $a_1neq$, умножаем строку $r_1$ на $frac$ (если $a_1=1$, то никакого домножения делать не надо). Далее с помощью строки $r_1$ производим обнуление всех остальных ненулевых элементов первого столбца, после чего переходим к следующему шагу.

На втором шаге прямого хода работаем с второй строкой $r_2$. Второй элемент этой строки обозначим как $a_2$. Если $a_2=0$, то меняем местами вторую строку с одной из тех нижележащих строк, у которых второй элемент отличен от нуля. Если таких строк нет, т.е. у всех нижележащих строк второй элемент равен нулю, то прекращаем решение, так как обратная матрица $A^$ не существует. Затем, если $a_2neq$, умножаем строку $r_2$ на $frac$ (если $a_2=1$, то никакого домножения делать не надо). Далее с помощью строки $r_2$ производим обнуление всех остальных ненулевых элементов второго столбца, после чего переходим к следующему шагу.

Полагаю, логика данного метода ясна. На k-м шаге работаем с k-й строкой $r_k$, k-й элемент которой обозначим как $a_k$. Если $a_k=0$, то меняем местами строку $r_k$ с одной из тех нижележащих строк, у которых k-й элемент отличен от нуля. Если таких строк нет, т.е. у всех нижележащих строк k-й элемент равен нулю, то прекращаем решение, так как обратная матрица $A^$ не существует. Затем, если $a_kneq$, умножаем строку $r_k$ на $frac$ (если $a_k=1$, то никакого домножения делать не надо). Далее с помощью строки $r_k$ производим обнуление всех остальных ненулевых элементов k-го столбца, после чего переходим к следующему шагу.

Когда мы обработаем последнюю строку, матрица до черты станет единичной, и алгоритм завершится.

Перед тем, как переходить к примерам, я введу один дополнительный термин: ведущий элемент. Ведущим элементом ненулевой строки называется её первый (считая слева направо) отличный от нуля элемент. Например, в строке $(0;0;5;-9;0)$ ведущим будет третий элемент (он равен 5).

Найти матрицу $A^$, если $A=left(begin -5 & 23 & -24\ -1 & 4 & -5\ 9 & -40 & 43 end right)$.

Заданная нам матрица не имеет нулевых строк или столбцов, поэтому можем приступать к нахождению $A^$. Поставленную задачу решим двумя способами: как преобразованиями метода Гаусса, так и метода Гаусса-Жордана. Для начала запишем матрицу $(A|E)$, которая в нашем случае будет иметь такой вид:

$$ left(begin -5 & 23 & -24 & 1 & 0 & 0\ -1 & 4 & -5 & 0 & 1 & 0\ 9 & -40 & 43 & 0 & 0 & 1 endright) $$

Наша цель: привести матрицу $(A|E)$ к виду $left(E|A^right)$.

Видео:Математика без Ху!ни. Метод Гаусса.Скачать

Метод Гаусса

Видео:Урок 1. Матрицы, определитель матрицы и ранг матрицы | Высшая математика | TutorOnlineСкачать

Прямой ход метода Гаусса

На первом шаге прямого хода мы работаем с первой строкой. Первый элемент этой строки (число -5) не равен нулю, поэтому можем приступать к обнулению ненулевых элементов первого столбца, расположенных под первой строкой. Однако для тех преобразований, которые мы станем делать для обнуления элементов, удобно, когда ведущий элемент используемой строки равен 1 или -1. Почему это так, станет ясно из дальнейших действий. Чтобы ведущий элемент текущей строки стал равен -1, поменяем местами первую строку с одной из нижележащих строк – с второй строкой:

$$ left(begin -5 & 23 & -24 & 1 & 0 & 0\ -1 & 4 & -5 & 0 & 1 & 0\ 9 & -40 & 43 & 0 & 0 & 1 endright) overset<r_1leftrightarrow> left(begin boldred & 4 & -5 & 0 & 1 & 0\ normblue & 23 & -24 & 1 & 0 & 0\ normblue & -40 & 43 & 0 & 0 & 1 endright) $$

Теперь ведущий элемент первой строки стал равен -1 (я выделил этот элемент красным цветом). Приступим к обнулению ненулевых элементов первого столбца, лежащих под первой строкой (они выделены синим цветом). Для этого над строками матрицы нужно выполнить такие действия:

Запись $r_2-5r_1$ означает, что от элементов второй строки вычли соответствующие элементы первой строки, умноженные на пять. Результат записывают на место второй строки в новую матрицу. Если с устным выполнением такой операции возникают сложности, то это действие можно выполнить отдельно:

Действие $r_3+9r_1$ выполняется аналогично. Первую строку мы не трогали, поэтому в новую матрицу она перейдёт без изменений:

$$ left(begin -1 & 4 & -5 & 0 & 1 & 0\ -5 & 23 & -24 & 1 & 0 & 0\ 9 & -40 & 43 & 0 & 0 & 1 endright) begin phantom\ r_2-5r_1 \ r_3+9r_1 end rightarrow left(begin -1 & 4 & -5 & 0 & 1 & 0\ 0 & 3 & 1 & 1 & -5 & 0\ 0 & -4 & -2 & 0 & 9 & 1 endright) $$

На этом первый шаг закончен. Нулевых строк в матрице до черты не возникло, поэтому продолжаем решение. Кстати, теперь, я полагаю, ясно, зачем надо было менять местами строки. Если бы не смена мест строк, нам пришлось бы выполнять действия $r_2-fraccdot$ и $r_3+fraccdot$, что привело бы к появлению дробей. А легче, разумеется, работать с целыми числами, чем с дробями.

На втором шаге прямого хода мы работаем с второй строкой. Второй элемент этой строки (число 3) не равен нулю, поэтому можем приступать к обнулению ненулевых элементов второго столбца, расположенных под второй строкой:

$$ left(begin -1 & 4 & -5 & 0 & 1 & 0\ 0 & 3 & 1 & 1 & -5 & 0\ 0 & -4 & -2 & 0 & 9 & 1 endright) begin phantom\ phantom \ r_3+4/3cdot end rightarrow left(begin -1 & 4 & -5 & 0 & 1 & 0\ 0 & 3 & 1 & 1 & -5 & 0\ 0 & 0 & -2/3 & 4/3 & 7/3 & 1 endright) $$

Матрица до черты стала верхней треугольной, поэтому прямой ход метода Гаусса окончен.

Пару слов насчёт действий со строками, которые мы выполняли на втором шаге. На первом шаге мы меняли местами строки, чтобы ведущий элемент первой строки стал равен -1. Здесь такая смена строк ничего не даст, так как доступна к обмену лишь третья строка, а у неё ведущий элемент тоже не равен ни 1, ни -1. В этом случае можно выполнить дополнительное преобразование со второй строкой: $r_2+r_3$:

$$ left(begin -1 & 4 & -5 & 0 & 1 & 0\ 0 & 3 & 1 & 1 & -5 & 0\ 0 & -4 & -2 & 0 & 9 & 1 endright) begin phantom\ r_2+r_3 \ phantom end rightarrow left(begin -1 & 4 & -5 & 0 & 1 & 0\ 0 & -1 & -1 & 1 & 4 & 1\ 0 & -4 & -2 & 0 & 9 & 1 endright) $$

После этого текущий шаг прямого хода будет продолжен без дробей. Можно было сделать и такое действие: $3r_3+4r_2$, тогда и необходимый элемент третьего столбца был бы обнулён, и дробей бы не появилось. Выполнять такие действия или нет – надо смотреть по ситуации. Если работы с дробями предвидится немного, то особого смысла в попытках их избежать нет. Если же нас ожидают ещё несколько шагов прямого хода, то, возможно, лучше упростить себе расчёты и выполнить вспомогательное действие, чтобы потом не работать с дробями. К слову, если есть необходимость избавиться от дробей в некоей строке, то можно просто домножить данную строку на соответствующий коэффициент. Например, строку $left(frac;;-frac;;2;0right)$ можно домножить на число 15, тогда дроби исчезнут, и строка станет такой: $left(5;;-12;;30;0right)$.

Видео:Матричное уравнениеСкачать

Обратный ход метода Гаусса

На первом шаге обратного хода мы работаем с последней, т.е. третьей строкой матрицы. Посмотрим на диагональный элемент в третьей строке: он равен $-frac$. Сделаем этот элемент единицей, домножив третью строку на $-frac$, а затем с помощью третьей строки обнулим ненулевые элементы третьего столбца, расположенные над третьей строкой:

$$ left(begin -1 & 4 & -5 & 0 & 1 & 0\ 0 & 3 & 1 & 1 & -5 & 0\ 0 & 0 & -2/3 & 4/3 & 7/3 & 1 endright) begin phantom\ phantom\ -3/2cdot end rightarrow\ left(begin -1 & 4 & -5 & 0 & 1 & 0\ 0 & 3 & 1 & 1 & -5 & 0\ 0 & 0 & 1 & -2 & -7/2 & -3/2 endright) begin r_1+5r_3 phantom\ r_2-r_3\ phantom end rightarrow left(begin -1 & 4 & 0 & -10 & -33/2 & -15/2\ 0 & 3 & 0 & 3 & -3/2 & 3/2\ 0 & 0 & 1 & -2 & -7/2 & -3/2 endright) $$

На втором шаге обратного хода мы работаем с предпоследней, т.е. второй строкой матрицы. Посмотрим на диагональный элемент во второй строке: он равен 3. Сделаем этот элемент единицей, домножив вторую строку на $frac$, а затем с помощью второй строки обнулим ненулевой элемент второго столбца, расположенный над второй строкой:

$$ left(begin -1 & 4 & 0 & -10 & -33/2 & -15/2\ 0 & 3 & 0 & 3 & -3/2 & 3/2\ 0 & 0 & 1 & -2 & -7/2 & -3/2 endright) begin phantom\ 1/3cdot \ phantom end rightarrow\ left(begin -1 & 4 & 0 & -10 & -33/2 & -15/2\ 0 & 1 & 0 & 1 & -1/2 & 1/2\ 0 & 0 & 1 & -2 & -7/2 & -3/2 endright) begin r_1-4r_2\ phantom \ phantom end rightarrow left(begin -1 & 0 & 0 & -14 & -29/2 & -19/2\ 0 & 1 & 0 & 1 & -1/2 & 1/2\ 0 & 0 & 1 & -2 & -7/2 & -3/2 endright) $$

Работаем с первой строкой. Сделаем диагональный элемент в первой строке (число -1) равным единице, домножив первую строку на -1:

$$ left(begin -1 & 0 & 0 & -14 & -29/2 & -19/2\ 0 & 1 & 0 & 1 & -1/2 & 1/2\ 0 & 0 & 1 & -2 & -7/2 & -3/2 endright) begin -1cdot\ phantom \ phantom end rightarrow left(begin 1 & 0 & 0 & 14 & 29/2 & 19/2\ 0 & 1 & 0 & 1 & -1/2 & 1/2\ 0 & 0 & 1 & -2 & -7/2 & -3/2 endright) $$

Матрица до черты стала единичной, преобразования завершены. Обратная матрица будет такой:

$$ A^ =left(begin 14 & 29/2 & 19/2\ 1 & -1/2 & 1/2\ -2 & -7/2 & -3/2 endright) $$

Если пропустить все пояснения, то решение будет таким:

$$ left(begin -5 & 23 & -24 & 1 & 0 & 0\ -1 & 4 & -5 & 0 & 1 & 0\ 9 & -40 & 43 & 0 & 0 & 1 endright) overset<r_1leftrightarrow> $$ $$ rightarrowleft(begin -1 & 4 & -5 & 0 & 1 & 0\ -5 & 23 & -24 & 1 & 0 & 0\ 9 & -40 & 43 & 0 & 0 & 1 endright) begin phantom\ r_2-5r_1 \ r_3+9r_1 end rightarrow left(begin -1 & 4 & -5 & 0 & 1 & 0\ 0 & 3 & 1 & 1 & -5 & 0\ 0 & -4 & -2 & 0 & 9 & 1 endright) begin phantom\ phantom \ r_3+4/3cdot end rightarrow $$ $$ rightarrowleft(begin -1 & 4 & -5 & 0 & 1 & 0\ 0 & 3 & 1 & 1 & -5 & 0\ 0 & 0 & -2/3 & 4/3 & 7/3 & 1 endright) begin phantom\ phantom\ -3/2cdot end rightarrow left(begin -1 & 4 & -5 & 0 & 1 & 0\ 0 & 3 & 1 & 1 & -5 & 0\ 0 & 0 & 1 & -2 & -7/2 & -3/2 endright) begin r_1+5r_3 phantom\ r_2-r_3\ phantom end rightarrow $$ $$ rightarrowleft(begin -1 & 4 & 0 & -10 & -33/2 & -15/2\ 0 & 3 & 0 & 3 & -3/2 & 3/2\ 0 & 0 & 1 & -2 & -7/2 & -3/2 endright) begin phantom\ 1/3cdot \ phantom end rightarrow left(begin -1 & 4 & 0 & -10 & -33/2 & -15/2\ 0 & 1 & 0 & 1 & -1/2 & 1/2\ 0 & 0 & 1 & -2 & -7/2 & -3/2 endright) begin r_1-4r_2\ phantom \ phantom end rightarrow $$ $$ rightarrowleft(begin -1 & 0 & 0 & -14 & -29/2 & -19/2\ 0 & 1 & 0 & 1 & -1/2 & 1/2\ 0 & 0 & 1 & -2 & -7/2 & -3/2 endright) begin -1cdot\ phantom \ phantom end rightarrow left(begin 1 & 0 & 0 & 14 & 29/2 & 19/2\ 0 & 1 & 0 & 1 & -1/2 & 1/2\ 0 & 0 & 1 & -2 & -7/2 & -3/2 endright) $$

Теперь решим этот же пример методом Гаусса-Жордана.

Видео:Метод Гаусса для решения систем линейных уравнений. Элементарные преобразования матриц.Скачать

Метод Гаусса-Жордана

На первом шаге мы работаем с первой строкой. Первый элемент этой строки (число -5) не равен нулю, поэтому можем следовать стандартному алгоритму: домножить первую строку на $-frac$, чтобы первый элемент стал равен единице, а затем обнулить все иные ненулевые элементы первого столбца. Однако, как и при решении методом Гаусса, удобно, когда ведущий элемент используемой строки равен 1 или -1. Поэтому как и на первом шаге метода Гаусса, поменяем местами первую строку с второй строкой:

$$ left(begin -5 & 23 & -24 & 1 & 0 & 0\ -1 & 4 & -5 & 0 & 1 & 0\ 9 & -40 & 43 & 0 & 0 & 1 endright) overset<r_1leftrightarrow> left(begin -1 & 4 & -5 & 0 & 1 & 0\ normblue & 23 & -24 & 1 & 0 & 0\ normblue & -40 & 43 & 0 & 0 & 1 endright) $$

Теперь первый элемент первой строки стал равен -1. Чтобы этот элемент стал равен 1, домножим первую строку на -1, а потом обнулим все остальные ненулевые элементы первого столбца (они выделены в матрице выше синим цветом):

$$ left(begin -1 & 4 & -5 & 0 & 1 & 0\ -5 & 23 & -24 & 1 & 0 & 0\ 9 & -40 & 43 & 0 & 0 & 1 endright) begin -1cdot\ phantom \ phantom end rightarrow\ rightarrowleft(begin 1 & -4 & 5 & 0 & -1 & 0\ -5 & 23 & -24 & 1 & 0 & 0\ 9 & -40 & 43 & 0 & 0 & 1 endright) begin phantom\ r_2+5r_1 \ r_3-9r_1 end rightarrow left(begin 1 & -4 & 5 & 0 & -1 & 0\ 0 & 3 & 1 & 1 & -5 & 0\ 0 & -4 & -2 & 0 & 9 & 1 endright) $$

На этом первый шаг закончен. Нулевых строк в матрице до черты не возникло, поэтому продолжаем решение.

На втором шаге мы работаем с второй строкой. Второй элемент этой строки (число 3) не равен нулю, поэтому домножаем вторую строку на $frac$, чтобы второй элемент стал равен единице, а затем обнуляем все иные ненулевые элементы второго столбца.

$$ left(begin 1 & -4 & 5 & 0 & -1 & 0\ 0 & 3 & 1 & 1 & -5 & 0\ 0 & -4 & -2 & 0 & 9 & 1 endright) begin phantom\1/3cdot \phantomend rightarrow\ rightarrowleft(begin 1 & -4 & 5 & 0 & -1 & 0\ 0 & 1 & 1/3 & 1/3 & -5/3 & 0\ 0 & -4 & -2 & 0 & 9 & 1 endright) begin r_1+4r_2\ phantom \ r_3+4r_2 end rightarrow left(begin 1 & 0 & 19/3 & 4/3 & -23/3 & 0\ 0 & 1 & 1/3 & 1/3 & -5/3 & 0\ 0 & 0 & -2/3 & 4/3 & 7/3 & 1 endright) $$

Замечание относительно облегчения работы с дробями, сделанное после второго шага прямого хода метода Гаусса, остаётся в силе и здесь.

На третьем шаге мы работаем с третьей строкой. Третий элемент этой строки (число -2/3) не равен нулю, поэтому домножаем третью строку на $-frac$, чтобы третий элемент стал равен единице, а затем обнуляем все иные ненулевые элементы третьего столбца.

$$ left(begin 1 & 0 & 19/3 & 4/3 & -23/3 & 0\ 0 & 1 & 1/3 & 1/3 & -5/3 & 0\ 0 & 0 & -2/3 & 4/3 & 7/3 & 1 endright) begin phantom\phantom \ -3/2cdotend rightarrow\ rightarrowleft(begin 1 & 0 & 19/3 & 4/3 & -23/3 & 0\ 0 & 1 & 1/3 & 1/3 & -5/3 & 0\ 0 & 0 & 1 & -2 & -7/2 & -3/2 endright) begin r_1-19/3r_3\ r_2-1/3cdot \ phantom end rightarrow left(begin 1 & 0 & 0 & 14 & 29/2 & 19/2\ 0 & 1 & 0 & 1 & -1/2 & 1/2\ 0 & 0 & 1 & -2 & -7/2 & -3/2 endright) $$

Матрица до черты стала единичной, преобразования завершены. Обратная матрица будет такой:

$$ A^ =left(begin 14 & 29/2 & 19/2\ 1 & -1/2 & 1/2\ -2 & -7/2 & -3/2 endright) $$

Если пропустить все пояснения, то решение будет таким:

$$ left(begin -5 & 23 & -24 & 1 & 0 & 0\ -1 & 4 & -5 & 0 & 1 & 0\ 9 & -40 & 43 & 0 & 0 & 1 endright) overset<r_1leftrightarrow> left(begin -1 & 4 & -5 & 0 & 1 & 0\ -5 & 23 & -24 & 1 & 0 & 0\ 9 & -40 & 43 & 0 & 0 & 1 endright) begin -1cdot\ phantom \ phantom end rightarrow $$ $$ rightarrowleft(begin 1 & -4 & 5 & 0 & -1 & 0\ -5 & 23 & -24 & 1 & 0 & 0\ 9 & -40 & 43 & 0 & 0 & 1 endright) begin phantom\ r_2+5r_1 \ r_3-9r_1 end rightarrow left(begin 1 & -4 & 5 & 0 & -1 & 0\ 0 & 3 & 1 & 1 & -5 & 0\ 0 & -4 & -2 & 0 & 9 & 1 endright) begin phantom\1/3cdot \phantomend rightarrow $$ $$ rightarrowleft(begin 1 & -4 & 5 & 0 & -1 & 0\ 0 & 1 & 1/3 & 1/3 & -5/3 & 0\ 0 & -4 & -2 & 0 & 9 & 1 endright) begin r_1+4r_2\ phantom \ r_3+4r_2 end rightarrow left(begin 1 & 0 & 19/3 & 4/3 & -23/3 & 0\ 0 & 1 & 1/3 & 1/3 & -5/3 & 0\ 0 & 0 & -2/3 & 4/3 & 7/3 & 1 endright) begin phantom\phantom \ -3/2cdotend rightarrow $$ $$ rightarrowleft(begin 1 & 0 & 19/3 & 4/3 & -23/3 & 0\ 0 & 1 & 1/3 & 1/3 & -5/3 & 0\ 0 & 0 & 1 & -2 & -7/2 & -3/2 endright) begin r_1-19/3r_3\ r_2-1/3cdot \ phantom end rightarrow left(begin 1 & 0 & 0 & 14 & 29/2 & 19/2\ 0 & 1 & 0 & 1 & -1/2 & 1/2\ 0 & 0 & 1 & -2 & -7/2 & -3/2 endright) $$

Ответ: $A^ =left(begin 14 & 29/2 & 19/2\ 1 & -1/2 & 1/2\ -2 & -7/2 & -3/2 endright)$.

Найти матрицу $A^$, если $A=left(begin -2 & 3 & 0 & 1\ -6 & 9 & -2 & 7\ 0 & -2 & -18 & 27\ -4 & 5 & -8 & 14end right)$.

В предыдущем примере были даны подробные пояснения каждого шага как метода Гаусса, так и метода Гаусса-Жордана. В этом примере я стану комментировать лишь некие нюансы, которые возникнут в ходе решения.

Видео:Решение системы уравнений методом обратной матрицы.Скачать

Метод Гаусса

Пора переходить ко второму шагу прямого хода метода Гаусса. На этом шаге должна использоваться вторая строка, однако второй элемент данной строки равен нулю. Согласно алгоритму, нужно поменять местами вторую строку с одной из нижележащих строк, у которых второй элемент отличен от нуля. Поменяем местами вторую и четвёртую строки, а потом продолжим преобразования:

$$ left(begin -2 & 3 & 0 & 1 & 1 & 0 & 0 & 0\ 0 & 0 & -2 & 4 & -3 & 1 & 0 & 0 \ 0 & -2 & -18 & 27 & 0 & 0 & 1 & 0\ 0 & -1 & -8 & 12 & -2 & 0 & 0 & 1 end right) overset<r_2leftrightarrow> left(begin -2 & 3 & 0 & 1 & 1 & 0 & 0 & 0\ 0 & -1 & -8 & 12 & -2 & 0 & 0 & 1\ 0 & -2 & -18 & 27 & 0 & 0 & 1 & 0\ 0 & 0 & -2 & 4 & -3 & 1 & 0 & 0 end right) begin phantom \ phantom \ r_3-2r_2 \ phantom end rightarrow $$ $$ rightarrowleft(begin -2 & 3 & 0 & 1 & 1 & 0 & 0 & 0\ 0 & -1 & -8 & 12 & -2 & 0 & 0 & 1\ 0 & 0 & -2 & 3 & 4 & 0 & 1 & -2\ 0 & 0 & -2 & 4 & -3 & 1 & 0 & 0 end right) begin phantom \ phantom \ phantom \ r_4-r_3 end rightarrow $$ $$ rightarrowleft(begin -2 & 3 & 0 & 1 & 1 & 0 & 0 & 0\ 0 & -1 & -8 & 12 & -2 & 0 & 0 & 1\ 0 & 0 & -2 & 3 & 4 & 0 & 1 & -2\ 0 & 0 & 0 & 1 & -7 & 1 & -1 & 2 end right) begin r_1-r_4 \ r_2-12r_4 \ r_3-3r_1 \ phantom end rightarrow $$ $$ rightarrowleft(begin -2 & 3 & 0 & 0 & 8 & -1 & 1 & -2\ 0 & -1 & -8 & 0 & 82 & -12 & 12 & -23\ 0 & 0 & -2 & 0 & 25 & -3 & 4 & -8\ 0 & 0 & 0 & 1 & -7 & 1 & -1 & 2 end right) begin phantom \ phantom \ -1/2cdot \ phantom end rightarrow $$ $$ rightarrowleft(begin -2 & 3 & 0 & 0 & 8 & -1 & 1 & -2\ 0 & -1 & -8 & 0 & 82 & -12 & 12 & -23\ 0 & 0 & 1 & 0 & -25/2 & 3/2 & -2 & 4\ 0 & 0 & 0 & 1 & -7 & 1 & -1 & 2 end right) begin phantom \ r_2+8r_3 \ phantom \ phantom end rightarrow $$ $$ rightarrowleft(begin -2 & 3 & 0 & 0 & 8 & -1 & 1 & -2\ 0 & -1 & 0 & 0 & -18 & 0 & -4 & 9\ 0 & 0 & 1 & 0 & -25/2 & 3/2 & -2 & 4\ 0 & 0 & 0 & 1 & -7 & 1 & -1 & 2 end right) begin phantom \ -1cdot \ phantom \ phantom end rightarrow $$ $$ rightarrowleft(begin -2 & 3 & 0 & 0 & 8 & -1 & 1 & -2\ 0 & 1 & 0 & 0 & 18 & 0 & 4 & -9\ 0 & 0 & 1 & 0 & -25/2 & 3/2 & -2 & 4\ 0 & 0 & 0 & 1 & -7 & 1 & -1 & 2 end right) begin r_1-3r_2 \ phantom \ phantom \ phantom end rightarrow $$ $$ rightarrowleft(begin -2 & 0 & 0 & 0 & -46 & -1 & -11 & 25\ 0 & 1 & 0 & 0 & 18 & 0 & 4 & -9\ 0 & 0 & 1 & 0 & -25/2 & 3/2 & -2 & 4\ 0 & 0 & 0 & 1 & -7 & 1 & -1 & 2 end right) begin -1/2cdot \ phantom \ phantom \ phantom end rightarrow $$ $$ rightarrowleft(begin 1 & 0 & 0 & 0 & 23 & 1/2 & 11/2 & -25/2\ 0 & 1 & 0 & 0 & 18 & 0 & 4 & -9\ 0 & 0 & 1 & 0 & -25/2 & 3/2 & -2 & 4\ 0 & 0 & 0 & 1 & -7 & 1 & -1 & 2 endright) $$

Из последней матрицы получаем ответ:

$$ A^ =left(begin 23 & 1/2 & 11/2 & -25/2\ 18 & 0 & 4 & -9\ -25/2 & 3/2 & -2 & 4\ -7 & 1 & -1 & 2 endright) $$

Видео:Обратная матрица методом элементарных преобразованийСкачать

Метод Гаусса-Жордана

Пора переходить ко второму шагу метода Гаусса-Жордана. На этом шаге должна использоваться вторая строка, однако второй элемент данной строки равен нулю. Согласно алгоритму, нужно поменять местами вторую строку с одной из нижележащих строк, у которых второй элемент отличен от нуля. Поменяем местами вторую и четвёртую строки, а потом продолжим преобразования:

$$ left(begin 1 & -3/2 & 0 & -1/2 & -1/2 & 0 & 0 & 0\ 0 & 0 & -2 & 4 & -3 & 1 & 0 & 0 \ 0 & -2 & -18 & 27 & 0 & 0 & 1 & 0\ 0 & -1 & -8 & 12 & -2 & 0 & 0 & 1 end right) overset<r_2leftrightarrow> $$ $$ rightarrowleft(begin 1 & -3/2 & 0 & -1/2 & -1/2 & 0 & 0 & 0\ 0 & -1 & -8 & 12 & -2 & 0 & 0 & 1 \ 0 & -2 & -18 & 27 & 0 & 0 & 1 & 0\ 0 & 0 & -2 & 4 & -3 & 1 & 0 & 0 end right) begin phantom \ -1cdot \ phantom \ phantom end rightarrow $$ $$ rightarrowleft(begin 1 & -3/2 & 0 & -1/2 & -1/2 & 0 & 0 & 0\ 0 & 1 & 8 & -12 & 2 & 0 & 0 & -1 \ 0 & -2 & -18 & 27 & 0 & 0 & 1 & 0\ 0 & 0 & -2 & 4 & -3 & 1 & 0 & 0 end right) begin r_1+3/2cdot \ phantom \ r_3+2r_2 \ phantom end rightarrow $$ $$ rightarrowleft(begin 1 & 0 & 12 & -37/2 & 5/2 & 0 & 0 & -3/2\ 0 & 1 & 8 & -12 & 2 & 0 & 0 & -1 \ 0 & 0 & -2 & 3 & 4 & 0 & 1 & -2\ 0 & 0 & -2 & 4 & -3 & 1 & 0 & 0 end right) begin phantom \ phantom \ -1/2cdot \ phantom end rightarrow $$ $$ rightarrowleft(begin 1 & 0 & 12 & -37/2 & 5/2 & 0 & 0 & -3/2\ 0 & 1 & 8 & -12 & 2 & 0 & 0 & -1 \ 0 & 0 & 1 & -3/2 & -2 & 0 & -1/2 & 1\ 0 & 0 & -2 & 4 & -3 & 1 & 0 & 0 end right) begin r_1-12r_3 \ r_2-8r_3 \ phantom \ r_4+2r_3 end rightarrow $$ $$ rightarrowleft(begin 1 & 0 & 0 & -1/2 & 53/2 & 0 & 6 & -27/2\ 0 & 1 & 0 & 0 & 18 & 0 & 4 & -9 \ 0 & 0 & 1 & -3/2 & -2 & 0 & -1/2 & 1\ 0 & 0 & 0 & 1 & -7 & 1 & -1 & 2 end right) begin r_1+1/2cdot \ phantom \ r_3+3/2cdot \ phantom end rightarrow $$ $$ rightarrowleft(begin 1 & 0 & 0 & 0 & 23 & 1/2 & 11/2 & -25/2\ 0 & 1 & 0 & 0 & 18 & 0 & 4 & -9\ 0 & 0 & 1 & 0 & -25/2 & 3/2 & -2 & 4\ 0 & 0 & 0 & 1 & -7 & 1 & -1 & 2 endright) $$

Из последней матрицы получаем ответ:

$$ A^ =left(begin 23 & 1/2 & 11/2 & -25/2\ 18 & 0 & 4 & -9\ -25/2 & 3/2 & -2 & 4\ -7 & 1 & -1 & 2 endright) $$

Ответ: $ A^ =left(begin 23 & 1/2 & 11/2 & -25/2\ 18 & 0 & 4 & -9\ -25/2 & 3/2 & -2 & 4\ -7 & 1 & -1 & 2 endright) $.

Найти матрицу $A^$, если $A=left(begin 1 & -2 & 5\ -2 & 5 & -13\ -3 & 4 & -9end right)$.

В данном примере применим метод Гаусса.

$$ left(begin 1 & -2 & 5 & 1 & 0 & 0\ -2 & 5 & -13 & 0 & 1 & 0\ -3 & 4 & -9 & 0 & 0 & 1end right) begin phantom \ r_2+2r_1 \ r_3+3r_1 end rightarrow\ $$ $$ rightarrowleft(begin 1 & -2 & 5 & 1 & 0 & 0\ 0 & 1 & -3 & 2 & 1 & 0\ 0 & -2 & 6 & 3 & 0 & 1end right) begin phantom \ phantom \ r_3+2r_2 end rightarrow left(begin 1 & -2 & 5 & 1 & 0 & 0\ 0 & 1 & -3 & 2 & 1 & 0\ 0 & 0 & 0 & 7 & 2 & 1endright) $$

В матрице до черты появилась нулевая строка. Это означает, что обратная матрица $A^$ не существует.

Ответ: обратной матрицы не существует.

Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Метод Гаусса – теорема, примеры решений

Метод Гаусса – идеальный вариант для решения систем линейных алгебраических уравнений (далее СЛАУ). Благодаря методу Гаусса можно последовательно исключать неизвестные путём элементарных преобразований. Метод Гаусса – это классический метод решения СЛАУ, который и рассмотрен ниже.

Карл Фридрих Гаусс – немецкий математик, основатель одноименного метода решения СЛАУ

Карл Фридрих Гаусс – был известным великим математиком и его в своё время признали «королём математики». Хотя название «метод Гаусса» является общепринятым, Гаусс не является его автором: метод Гаусса был известен задолго до него. Первое его описание имеется в китайском трактате «Математика в девяти книгах», который составлен между II в. до н. э. и I в. н. э. и представляет собой компиляцию более ранних трудов, написанных примерно в X в. до н. э.

Метод Гаусса – последовательное исключение неизвестных. Этот метод используется для решения квадратных систем линейных алгебраических уравнений. Хотя уравнения при помощи метода Гаусса решаются легко, но всё же студенты часто не могут найти правильное решение, так как путаются в знаках (плюсы и минусы). Поэтому во время решения СЛАУ необходимо быть предельно внимательным и только тогда можно легко, быстро и правильно решить даже самое сложное уравнение.

У систем линейных алгебраических уравнений есть несколько преимуществ: уравнение не обязательно заранее на совместность; можно решать такие системы уравнений, в которых число уравнений не совпадает с количеством неизвестных переменных или определитель основной матрицы равняется нулю; есть возможность при помощи метода Гаусса приводить к результату при сравнительно небольшом количестве вычислительных операций.

Видео:Нахождение определителя путём элементарных преобразованийСкачать

Определения и обозначения

Как уже говорилось, метод Гаусса вызывает у студентов некоторые сложности. Однако, если выучить методику и алгоритм решения, сразу же приходит понимание в тонкостях решения.

Для начала систематизируем знания о системах линейных уравнений.

СЛАУ в зависимости от её элементов может иметь:

1. Одно решение;
2. много решений;
3. совсем не иметь решений.

В первых двух случаях СЛАУ называется совместимой, а в третьем случае – несовместима. Если система имеет одно решение, она называется определённой, а если решений больше одного, тогда система называется неопределённой.

Метод Крамера и матричный способ не подходят для решения уравнений, если система имеет бесконечное множество решений. Вот поэтому нам и нужен метод Гаусса, который поможет нам в любом случае найти правильное решение. К элементарным преобразованиям относятся:

• перемена мест уравнений системы;
• почленное умножение обеих частей на одно из уравнений на некоторое число, так, чтобы коэффициенты при первой переменной в двух уравнениях были противоположными числами;
• сложение к обеим частям одного из уравнений определённых частей другого уравнения.

Итак, когда мы знаем основные правила и обозначения, можно приступать к решению.

Теперь рассмотрим, как решаются системы методом Гаусса на простом примере:

где а, в, с – заданные коэффициенты, d – заданные свободные члены, x, y, z – неизвестные. Коэффициенты и свободные члены уравнения можно называть его элементами.

Если = = = , тогда система линейных алгебраических уравнений называется однородной, в другом случае – неоднородной.

Множественные числа , , называются решением СЛАУ, если при подстановке , , в СЛАУ получим числовые тождества.

Система, которую мы написали выше имеет координатную форму. Если её переделать в матричную форму, тогда система будет выглядеть так:

– это основная матрица СЛАУ.

– матрица столбец неизвестных переменных.

– матрица столбец свободных членов.

Если к основной матрице добавить в качестве – ого столбца матрицу-столбец свободных членов, тогда получится расширенная матрица систем линейных уравнений. Как правило, расширенная матрица обозначается буквой , а столбец свободных членов желательно отделить вертикальной линией от остальных столбцов. То есть, расширенная матрица выглядит так:

Если квадратная матрица равна нулю, она называется вырожденная, а если – матрица невырожденная.

Если с системой уравнений:

Произвести такие действия:

• умножать обе части любого из уравнений на произвольное и отличное от нуля число ;
• менять местами уравнения;
• к обеим частям любого из уравнений прибавить определённые части другого уравнения, которые умножаются на произвольное число ,

тогда получается эквивалентная система, у которой такое же решение или нет решений совсем.

Теперь можно перейти непосредственно к методу Гаусса.

Нужна помощь в написании работы?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.

Видео:Обратная матрицаСкачать

Простейшие преобразования элементов матрицы

Мы рассмотрели основные определения и уже понимаем, чем нам поможет метод Гаусса в решении системы. Теперь давайте рассмотрим простую систему уравнений. Для этого возьмём самое обычное уравнение, где и используем решение методом Гаусса:

Из уравнения запишем расширенную матрицу:

Из данной матрицы видно, по какому принципу она записана. Вертикальную черту не обязательно ставить, но просто так удобнее решать систему.

На матрице, которая написана выше рассмотрим, какие существуют элементарные преобразования:

1. В матрице строки можно переставлять местами. Например, в нашей матрице спокойно можно переставить первую и вторую строки:

.

2. Если в матрице имеются (или появились) пропорциональные строки (одинаковые), тогда необходимо оставить всего лишь одну строку, а остальные убрать (удалить).

3. Если в ходе преобразований в матрице появилась строка, где находятся одни нули, тогда такую строку тоже нужно удалять.

4. Строку матрицы можно умножать (делить) на любое число, которое отличное от нуля. Такое действие желательно проделывать, так как в будущем проще преобразовывать матрицу.

5. Сейчас рассмотрим преобразование, которое больше всего вызывает затруднение у студентов. Для этого возьмём изначальную нашу матрицу:

Для удобства умножаем первую строку на (-3):

Теперь ко второй строке прибавляем первую строку, которую умножали на -3. Вот что у нас получается:

В итоге получилось такое преобразование:

Теперь для проверки можно разделить все коэффициенты первой строки на те же и вот что получается:

В матрице верхняя строка преобразовалась:

Первую строку делим на и преобразовалась нижняя строка:

И верхнюю строку поделили на то же самое число :

Как вы можете убедиться, в итоге строка, которую мы прибавляли ни капельки не изменилась, а вот вторая строка поменялась. ВСЕГДА меняется только та строка, к которой прибавляются коэффициенты.

Мы расписали в таких подробностях, чтобы было вам понятно, откуда какая цифра взялась. На практике, например, на контрольной или экзамене матрица так подробно не расписывается. Как правило, в задании решение матрицы оформляется так:

.

Видео:Система линейных уравнений. Метод обратной матрицы. Матричный метод.Скачать

Алгоритм решения методом Гаусса пошагово

После того, как мы рассмотрели простейшие преобразования, в которых на помощь пришёл метод Гаусса, можем вернуться к нашей системе, которую уже разложили по полочкам и пошагово распишем:

Шаг 1. Переписываем систему в виде матрицы

Шаг 2. Преобразовываем матрицу: вторую строку в первом столбце приводим к нулю

Как мы привели вторую строку в первом столбце к нулю описано выше. Напомним, что первую строку умножали на и вторую строку прибавили к первой , умноженной на .

Шаг 3. Приводим матрицу к ступенчатому виду

Теперь вторую строку можно поделить на 2 и получается:

Верхнюю строку делим на и приводим матрицу к ступенчатому виду:

Когда оформляют задание, так и отчёркивают простым карандашом для упрощения работы, а также обводят те числа, которые стоят на “ступеньках”. Хотя в учебниках и другой литературе нет такого понятия, как ступенчатый вид. Как правило, математики такой вид называют трапециевидным или треугольным.

Шаг 4. Записываем эквивалентную систему

После наших элементарных преобразований получилась эквивалентная система:

Шаг 5. Производим проверку (решение системы обратным путём)

Теперь систему нужно решить в обратном направлении, то есть обратным ходом, начиная с последней строки.:

находим : ,

,

.

После находим :

,

.

.

Как видим, уравнение решено правильно, так как ответы в системе совпадают.

Видео:Ранг матрицы (метод элементарных преобразований, №619)Скачать

Решение систем линейных уравнений методом Гаусса, в которых основная матрица невырожденная, а количество в ней неизвестных равняется количеству уравнений

Как мы уже упоминали, невырожденная матрица бывает тогда, когда . Разберём систему уравнений невырожденной матрицы, где уравнений по количеству столько же, сколько и неизвестных. Эту систему уравнений решим другим способом.

Дана система уравнений:

Для начала нужно решить первое уравнение системы относительно неизвестной переменной . Далее подставим полученное выражение сначала во второе уравнение, а затем в третье, чтобы исключить из них эту переменную.

Теперь переходим ко второму уравнению системы относительно и полученный результат подставим в третье уравнение.. Это нужно для того, чтобы исключить неизвестную переменную :

Из последнего, третьего уравнения мы видим, что . Из второго уравнения находим . И последнее, находим первое уравнение .

Итак, мы нашли все три неизвестных при помощи последовательного исключения. Такой процесс называют – прямой ход метода Гаусса. Когда последовательно находятся неизвестные переменные, начиная с последнего уравнения, называется обратным ходом метода Гаусса.

Когда выражается через и в первом уравнении, а затем подставляется полученное выражение во второе или третье уравнения, тогда, чтобы привести в к такому же результату, необходимо проделать такие действия:

• берём второе уравнение и к его левой и правой частям прибавляем определённые части из первого уравнения, которые умножаются на ,
• берём третье уравнение и к его левой и правой частям прибавляем определённые части из первого уравнения, которые умножаются на .

И действительно, благодаря такой процедуре у нас есть возможность исключать неизвестную переменную со второго и третьего уравнения системы:

Возникают нюансы с исключением неизвестных переменных тогда, когда в уравнении системы нет каких-либо неизвестных переменных. Рассмотрим такую систему:

В этой системе в первом уравнении нет переменной и поэтому у нас нет возможности решить первое уравнение системы относительно , чтобы исключить данную переменную из остальных уравнений. В таком случае выход есть. Нужно всего лишь уравнения переставить местами.

Так как мы описываем уравнения системы, в которых определитель основных матриц отличен от нуля, тогда всегда есть такое уравнение, в котором есть необходимая нам переменная и это уравнение мы можем поставить туда, куда нам нужно.

В примере, который мы рассматриваем, достаточно всего лишь поменять местами первое и второе уравнение.

Теперь мы можем спокойно разрешить первое уравнение относительно переменной и убрать (исключить) из остальных уравнений в системе. Вот и весь принцип работы с такими, на первый взгляд, сложными системами.

Видео:8. Вычисление ранга матрицы методом элементарных преобразованийСкачать

Решение систем линейных уравнений методом Гаусса, в которых основная матрица вырожденная, а количество в ней неизвестных не совпадает с количеством уравнений

Метод Гаусса помогает решать системы уравнений, у которых основная матрица прямоугольная или квадратная, но основная вырожденная матрица может совсем не иметь решений, иметь бесконечное множество решений или иметь всего лишь одно единственное решение.

Рассмотрим, как при помощи метода Гаусса устанавливается совместность или несовместность систем линейных уравнений. В случае, если есть совместность определим все решения или одно решение.

В принципе, исключать неизвестные переменные можно точно так, как описано выше. Однако, есть некоторые непонятные ситуации, которые могут возникнуть в ходе решения:

1. На некоторых этапах в момент исключения неизвестных переменных некоторые уравнения могут обратиться в тождества . В данном случае такие уравнения лишние в системе и их можно смело полностью убирать, а затем продолжать решать уравнение методом Гаусса.

Например, вам попалась подобная система:

У нас получается такая ситуация

Как видим, второе уравнение . Соответственно, данное уравнение мы можем из системы удалить, так как оно без надобности.

Дальше можно продолжать решение системы линейных алгебраических уравнений уравнений традиционным методом Гаусса.

2. При решении уравнений прямым ходом методом Гаусса могут принять не только одно, но и несколько уравнений такой вид: , где – число, которое отличное от нуля. Это говорит о том, что такое уравнение никогда не сможет превратиться в тождество даже при любых значениях неизвестных переменных. То есть, можно выразить по-другому. Если уравнение приняло вид, значит система несовместна, то есть, не имеет решений. Рассмотрим на примере:

Для начала необходимо исключить неизвестную переменную из всех уравнений данной системы, начиная со второго уравнения. Для этого нужно прибавить к левой и правой частям второго, третьего, четвёртого уравнения части (левую и правую) первого уравнения, которые соответственно, умножаются на (-1), (-2), (-3). Получается:

В третьем уравнении получилось равенство . Оно не подходит ни для каких значений неизвестных переменных , и , и поэтому, у данной системы нет решений. То есть, говорится, что система не имеет решений.

3. Допустим, что при выполнении прямого хода методом Гаусса нам нужно исключить неизвестную переменную , и ранее, на каком-то этапе у нас уже исключалась вместе с переменной . Как вы поступите в таком случае? При таком положении нам нужно перейти к исключению переменной . Если же уже исключались, тогда переходим к , и т. д.

Рассмотрим систему уравнений на таком этапе, когда уже исключилась переменная :

Такая система уравнений после преобразования выглядит так:

Вы наверное уже обратили внимание, что вместе с исключились и . Поэтому решение методом Гаусса продолжаем исключением переменной из всех уравнений системы, а начнём мы с третьего уравнения:

Чтобы завершить уравнение прямым ходом метода Гаусса, необходимо исключить последнюю неизвестную переменную из последнего уравнения:

Допусти, что система уравнений стала:

В этой системе нет ни одного уравнения, которое бы сводилось к . В данном случае можно было бы говорить о несовместности системы. Дальше непонятно, что же делать? Выход есть всегда. Для начала нужно выписать все неизвестные, которые стоят на первом месте в системе:

В нашем примере это , и . В левой части системы оставим только неизвестные, которые выделены зелёным квадратом а в правую перенесём известные числа, но с противоположным знаком. Посмотрите на примере, как это выглядит:

Можно придать неизвестным переменным с правой части уравнений свободные (произвольные) значения: , , , где , , – произвольные числа.

Теперь в правых частях уравнений нашей системы имеются числа и можно приступать к обратному ходу решения методом Гаусса.

В последнем уравнении системы получилось: , и теперь мы легко найдём решение в предпоследнем уравнении: , а из первого уравнения получаем:

= =

В итоге, получился результат, который можно и записать.

Ответ

,

,

,

,

,

.

Видео:11. Ранг матрицыСкачать

Примеры решения методом Гаусса

Выше мы подробно расписали решение системы методом Гаусса. Чтобы закрепить материал, решим несколько примеров, в которых опять нам поможет метод Гаусса. Соответственно, начнём с самой простой системы.

Задача

Решить систему линейных алгебраических уравнений методом Гаусса:

Решение

Выписываем матрицу, куда добавляем столбец свободных членов:

Прежде всего мы смотрим на элемент, который находится в матрице в левом верхнем углу (первая строка, первый столбец). Для наглядности выделим цифру зелёным квадратом. На этом месте практически всегда стоит единица:

Так как мы должны использовать подходящее элементарное преобразование строк и сделать так, чтобы элемент, который находится в матрице под выделенной цифрой превратился в . Для этого можно ко второй строке прибавить первую строку и умножить на .Однако, не сильно хочется работать с дробями, поэтому давайте постараемся этого избежать. Для этого нужно вторую строку умножить на (разрешающий элемент данного шага).

Соответственно, первая строка остаётся неизменной, а вторая поменяется:

Подбираем такое элементарное преобразование строк, чтобы во второй строке в первом столбце образовался . Для этого первую строку нужно умножить на и только после этого ко второй строке прибавить изменённую после умножения на вторую строку. Вот что получилось:

. Теперь прибавляем со второй строки первую строку . У нас получился , который записываем во вторую строку в первый столбец. Также решаем и остальные элементы матрицы. Вот что у нас получилось:

Как всегда у нас первая строка осталась без изменений, а вторая с новыми числами.

Итак, у нас получился ступенчатый вид матрицы:

Записываем новую систему уравнений:

Для проверки решаем систему обратным ходом. Для этого находим сначала :

Так как найден, находим :

.

Подставляем в изначальную нашу систему уравнений найденные и :

и .

Как видите из решения, система уравнений решена верно. Запишем ответ.

Ответ

Выше мы решали систему уравнений в двумя неизвестными, а теперь рассмотрим систему уравнений с тремя неизвестными.

Задача

Решить систему уравнений методом Гаусса:

Решение

Составляем матрицу, куда вписываем и свободные члены:

Что нам надо? Чтобы вместо цифры 2 появился 0. Для этого подбираем ближайшее число. Например, можно взять цифру -2 и на неё перемножить все элементы первой строки. Значит, умножаем , а потом прибавляем, при этом задействуем вторую строку: . В итоге у нас получился нуль, который записываем во вторую строку в первый столбец. Затем , и . Аналогично, и . И умножаем свободный член . Так и запишем следующую матрицу. Не забывайте, что первая строка остаётся без изменений:

Дальше необходимо проделать те же самые действия по отношению к третьей строке. То есть, первую строку нужно умножать не на (-2), а на цифру 3, так как и в третьей строке нужно коэффициенты привести у нулю. Также первую строку умножаем на 3 и прибавляем третью строку. Получается так:

Теперь нужно обнулить элемент 7, который стоит в третьей строке во втором столбце. Для этого выбираем цифру (-7) и проделываем те же действия. Однако, необходимо задействовать вторую строку. То есть, вторую строку умножаем на (-7) и прибавляем с третьей строкой. Итак, . Записываем результат в третью строку. Такие же действия проделываем и с остальными элементами. Получается новая матрица:

В результате получилась ступенчатая система уравнений:

Сначала находим : ,

.

Обратный ход:

Итак, уравнение системы решено верно.

Ответ

,

,

.

Система с четырьмя неизвестными более сложная, так как в ней легко запутаться. Попробуем решить такую систему уравнений.

Задача

Решите систему уравнений методом Гаусса:

Решение

В уравнении , то есть – ведущий член и пусть ≠ 0

Из данного уравнения составим расширенную матрицу:

Теперь нужно умножить последние три строки (вторую, третью и четвёртую) на: , , . Затем прибавим полученный результат ко второй, третьей и четвёртой строкам исключаем переменную из каждой строки, начиная не с первой, а не со второй. Посмотрите, как изменилась наша новая матрица и в теперь стоит 0.

Поменяем вторую и третью строку местами и получим:

Получилось так, что = b и тогда, умножая вторую строку на (-7/4) и результат данной строки, прибавляя к четвёртой, можно исключить переменную из третьей и четвёртой строк:

Получилась такая матрица:

Также, учитывая, что = , умножим третью строку на: 13,5/8 = 27/16, и, полученный результат прибавим к четвёртой, чтобы исключить переменную и получаем новую систему уравнений:

Теперь необходимо решить уравнение обратным ходом и найдём из последнего, четвёртого уравнения ,

из третьего: = = =

второе уравнение находим: = = = 2,

из первого уравнения: = .

Значит, решение системы такое: (1, 2, -1, -2).

Ответ

,

,

,

.

Добавим ещё несколько примеров для закрепления материла, но без такого подробного описания, как предыдущие системы уравнений.

Задача

Решить систему уравнений методом Гаусса:

Решение

Записываем расширенную матрицу системы:

Сначала смотрим на левое верхнее число:

Как выше уже было сказано, на этом месте должна стоять единица, но не обязательно. Производим такие действия: первую строку умножаем на -3, а потом ко второй строке прибавляем первую:

Производим следующие действия: первую строку умножаем на -1. Затем к третьей строки прибавляем вторую:

Теперь вторую строку умножаем на 1, а затем к третьей строке прибавляем вторую:

Получился ступенчатый вид уравнения:

,

,

,

,

.

.

Ответ

,

,

.

Заключение

Итак, вы видите, что метод Гаусса – интересный и простой способ решения систем линейных алгебраических уравнений. Путём элементарных преобразований нужно из системы исключать неизвестные переменные, чтобы систему превратить в ступенчатый вид. Данный метод удобен тем, что всегда можно проверить, правильно ли решено уравнение. Нужно просто подставить найденные неизвестные в изначальную систему уравнений.

Если элементы определителя не равняются нулю, тогда лучше обратиться к методу Крамера, а если же элементы нулевые, тогда такие системы очень удобно решать благодаря методу Гаусса.

Предлагаем ещё почитать учебники, в которых также описаны решения систем методом Гаусса.

Литература для общего развития: