Данный онлайн калькулятор решает систему линейных уравнений матричным методом. Дается очень подробное решение. Для решения системы линейных уравнений выберите количество переменных. Выбирайте метод вычисления обратной матрицы. Затем введите данные в ячейки и нажимайте на кнопку «Вычислить».
- Предупреждение
- Матричный метод решения систем линейных уравнений
- Примеры решения системы линейных уравнений матричным методом
- Матричный метод решения СЛАУ: пример решения с помощью обратной матрицы
- Пример решения системы линейных уравнений с помощью метода обратной матрицы
- Решение матричных уравнений: теория и примеры
- Решение матричных уравнений: как это делается
- Решение матричных уравнений: примеры
- 📽️ Видео
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Видео:Матричный метод решения систем уравненийСкачать
Матричный метод решения систем линейных уравнений
Рассмотрим следующую систему линейных уравнений:
 | (1) |
Для решения системы линейных уравнений (1) матричным методом запишем ее матричном виде:
| Ax=b, | (2) |
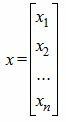   | (3) |
Мы будем предполагать, что матрица A имеет обратное, т.е. определитель матрицы A не равен нулю.
Умножим матричное уравнение (2) на обратную матрицу A −1 . Тогда
| A −1 Ax=A −1 b. | (4) |
Учитывая определение обратной матрицы, имеем A −1 A=E, где E— единичная матрица. Следовательно (4) можно записать так:
| Ex=A −1 b. | (4) |
или, учитывая, что Ex=x:
| x=A −1 b. | (5) |
Таким образом, для решения системы линейных уравнений (1) (или (2)), достаточно умножить обратную к A матрицу на вектор ограничений b.
Видео:Решение матричных уравненийСкачать
Примеры решения системы линейных уравнений матричным методом
Пример 1. Решить следующую систему линейных уравнений матричным методом:
 |
Матричный вид записи системы линейных уравнений: Ax=b, где
 . |
Найдем обратную к матрице A методом Жордана-Гаусса. С правой стороны матрицы A запишем единичную матрицу:
 . |
Выбираем самый большой по модулю ведущий элемент столбца 1. Для этого заменяем местами строки 1 и 2:
 . |
Исключим элементы 1-го столбца матрицы ниже главной диагонали. Для этого сложим строки 2,3 со строкой 1, умноженной на -1/3,-1/3 соответственно:
 . |
Выбираем самый большой по модулю ведущий элемент столбца 2. Для этого заменяем местами строки 2 и 3:
 . |
Исключим элементы 2-го столбца матрицы ниже главной диагонали. Для этого сложим строку 3 со строкой 2, умноженной на -24/51:
 . |
Исключим элементы 3-го столбца матрицы выше главной диагонали. Для этого сложим строки 1, 2 со строкой 3, умноженной на 17/53, 85/159 соответственно:
 . |
Исключим элементы 2-го столбца матрицы выше главной диагонали. Для этого сложим строку 1 со строкой 2, умноженной на -3/17:
 . |
Делим каждую строку матрицы на ведущий элемент соответствующей строки:
 . |
Отделяем правую часть матрицы. Полученная матрица является обратной матрицей к A :
 . |
Обратная матрица найдена. Решение системы линейных уравнений имеет вид x=A−1b. Тогда
  . |
 |
Пример 2. Решить следующую систему линейных уравнений матричным методом:
 . |
Матричный вид записи системы линейных уравнений: Ax=b, где
 . |
Найдем обратную к матрице A методом алгебраических дополнений. Вычислим определитель матрицы A :
 . |
Вычислим все алгебраические дополнения матрицы A:
 , |
 , |
 , |
 , |
 , |
 , |
 , |
 , |
 . |
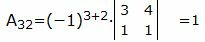Обратная матрица вычисляется из следующего выражения:
 |
где Aij − алгебраическое дополнение элемента матрицы A, находящиеся на пересечении i-ой строки и j-ого столбца, а Δ − определитель матрицы A.
Используя формулу обратной матрицы, получим:
  |
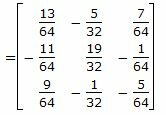Обратная матрица найдена. Решение системы линейных уравнений имеет вид x=A −1 b. Тогда
Видео:Система линейных уравнений. Метод обратной матрицы. Матричный метод.Скачать
Матричный метод решения СЛАУ: пример решения с помощью обратной матрицы
В данной статье мы расскажем о матричном методе решения системы линейных алгебраических уравнений, найдем его определение и приведем примеры решения.
Метод обратной матрицы — это метод, использующийся при решении СЛАУ в том случае, если число неизвестных равняется числу уравнений.
Найти решение системы n линейных уравнений с n неизвестными:
a 11 x 1 + a 12 x 2 + . . . + a 1 n x n = b 1 a n 1 x 1 + a n 2 x 2 + . . . + a n n x n = b n
Матричный вид записи: А × X = B
где А = а 11 а 12 ⋯ а 1 n а 21 а 22 ⋯ а 2 n ⋯ ⋯ ⋯ ⋯ а n 1 а n 2 ⋯ а n n — матрица системы.
X = x 1 x 2 ⋮ x n — столбец неизвестных,
B = b 1 b 2 ⋮ b n — столбец свободных коэффициентов.
Из уравнения, которое мы получили, необходимо выразить X . Для этого нужно умножить обе части матричного уравнения слева на A — 1 :
A — 1 × A × X = A — 1 × B .
Так как А — 1 × А = Е , то Е × X = А — 1 × В или X = А — 1 × В .
Обратная матрица к матрице А имеет право на существование только, если выполняется условие d e t A н е р а в е н н у л ю . Поэтому при решении СЛАУ методом обратной матрицы, в первую очередь находится d e t А .
В том случае, если d e t A н е р а в е н н у л ю , у системы имеется только один вариант решения: при помощи метода обратной матрицы. Если d e t А = 0 , то систему нельзя решить данным методом.
Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать
Пример решения системы линейных уравнений с помощью метода обратной матрицы
Решаем СЛАУ методом обратной матрицы:
2 x 1 — 4 x 2 + 3 x 3 = 1 x 1 — 2 x 2 + 4 x 3 = 3 3 x 1 — x 2 + 5 x 3 = 2
- Записываем систему в виде матричного уравнения А X = B , где
А = 2 — 4 3 1 — 2 4 3 — 1 5 , X = x 1 x 2 x 3 , B = 1 3 2 .
- Выражаем из этого уравнения X :
- Находим определитель матрицы А :
d e t A = 2 — 4 3 1 — 2 4 3 — 1 5 = 2 × ( — 2 ) × 5 + 3 × ( — 4 ) × 4 + 3 × ( — 1 ) × 1 — 3 × ( — 2 ) × 3 — — 1 × ( — 4 ) × 5 — 2 × 4 — ( — 1 ) = — 20 — 48 — 3 + 18 + 20 + 8 = — 25
d e t А не равняется 0, следовательно, для этой системы подходит метод решения обратной матрицей.
- Находим обратную матрицу А — 1 при помощи союзной матрицы. Вычисляем алгебраические дополнения А i j к соответствующим элементам матрицы А :
А 11 = ( — 1 ) ( 1 + 1 ) — 2 4 — 1 5 = — 10 + 4 = — 6 ,
А 12 = ( — 1 ) 1 + 2 1 4 3 5 = — ( 5 — 12 ) = 7 ,
А 13 = ( — 1 ) 1 + 3 1 — 2 3 — 1 = — 1 + 6 = 5 ,
А 21 = ( — 1 ) 2 + 1 — 4 3 — 1 5 = — ( — 20 + 3 ) = 17 ,
А 22 = ( — 1 ) 2 + 2 2 3 3 5 — 10 — 9 = 1 ,
А 23 = ( — 1 ) 2 + 3 2 — 4 3 — 1 = — ( — 2 + 12 ) = — 10 ,
А 31 = ( — 1 ) 3 + 1 — 4 3 — 2 4 = — 16 + 6 = — 10 ,
А 32 = ( — 1 ) 3 + 2 2 3 1 4 = — ( 8 — 3 ) = — 5 ,
А 33 = ( — 1 ) 3 + 3 2 — 4 1 — 2 = — 4 + 4 = 0 .
- Записываем союзную матрицу А * , которая составлена из алгебраических дополнений матрицы А :
А * = — 6 7 5 17 1 — 10 — 10 — 5 0
- Записываем обратную матрицу согласно формуле:
A — 1 = 1 d e t A ( A * ) T : А — 1 = — 1 25 — 6 17 — 10 7 1 — 5 5 — 10 0 ,
- Умножаем обратную матрицу А — 1 на столбец свободных членов В и получаем решение системы:
X = A — 1 × B = — 1 25 — 6 17 — 10 7 1 — 5 5 — 10 0 1 3 2 = — 1 25 — 6 + 51 — 20 7 + 3 — 10 5 — 30 + 0 = — 1 0 1
Ответ: x 1 = — 1 ; x 2 = 0 ; x 3 = 1
Видео:Лекция 8. Решение матричных уравненийСкачать
Решение матричных уравнений: теория и примеры
Видео:Матричные уравнения Полный разбор трех типов матричных уравненийСкачать
Решение матричных уравнений: как это делается
Матричные уравнения имеют прямую аналогию с простыми алгебраическими уравнениями, в которых присутствует операция умножения. Например,
где x — неизвестное.
А, поскольку мы уже умеем находить произведение матриц, то можем приступать к рассмотрению аналогичных уравнений с матрицами, в которых буквы — это матрицы.
Итак, матричным уравнением называется уравнение вида
где A и B — известные матрицы, X — неизвестная матрица, которую требуется найти.
Как решить матричное уравнение в первом случае? Для того, чтобы решить матричное уравнение вида A ⋅ X = B , обе его части следует умножить на обратную к A матрицу 
слева:
.
По определению обратной матрицы, произведение обратной матрицы на данную исходную матрицу равно единичной матрице: 
, поэтому
.
Так как E — единичная матрица, то E ⋅ X = X . В результате получим, что неизвестная матрица X равна произведению матрицы, обратной к матрице A , слева, на матрицу B :
.
Как решить матричное уравнение во втором случае? Если дано уравнение
то есть такое, в котором в произведении неизвестной матрицы X и известной матрицы A матрица A находится справа, то нужно действовать аналогично, но меняя направление умножения на матрицу, обратную матрице A , и умножать матрицу B на неё справа:
,
,
.
Как видим, очень важно, с какой стороны умножать на обратную матрицу, так как 
. Обратная к A матрица умножается на матрицу B с той стороны, с которой матрица A умножается на неизвестную матрицу X . То есть с той стороны, где в произведении с неизвестной матрицей находится матрица A .
Как решить матричное уравнение в третьем случае? Встречаются случаи, когда в левой части уравнения неизвестная матрица X находится в середине произведения трёх матриц. Тогда известную матрицу из правой части уравнения следует умножить слева на матрицу, обратную той, которая в упомянутом выше произведении трёх матриц была слева, и справа на матрицу, обратную той матрице, которая располагалась справа. Таким образом, решением матричного уравнения
.
Видео:Математика без Ху!ни. Метод Гаусса.Скачать
Решение матричных уравнений: примеры
Пример 1. Решить матричное уравнение
.
Решение. Данное уравнение имеет вид A ⋅ X = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится слева. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A слева. Найдём матрицу, обратную матрице A .
Сначала найдём определитель матрицы A :
.
Найдём алгебраические дополнения матрицы A :
.
Составим матрицу алгебраических дополнений:
.
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :
.
Теперь у нас есть всё, чтобы найти матрицу, обратную матрице A :
.
Наконец, находим неизвестную матрицу:
Пример 2. Решить матричное уравнение
.
Пример 3. Решить матричное уравнение
.
Решение. Данное уравнение имеет вид X ⋅ A = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится справа. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A справа. Найдём матрицу, обратную матрице A .
Сначала найдём определитель матрицы A :
.
Найдём алгебраические дополнения матрицы A :
.
Составим матрицу алгебраических дополнений:
.
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :
.
Находим матрицу, обратную матрице A :
.
Находим неизвестную матрицу:
До сих пор мы решали уравнения с матрицами второго порядка, а теперь настала очередь матриц третьего порядка.
Пример 4. Решить матричное уравнение
.
Решение. Это уравнение первого вида: A ⋅ X = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится слева. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A слева. Найдём матрицу, обратную матрице A .
Сначала найдём определитель матрицы A :
.
Найдём алгебраические дополнения матрицы A :
Составим матрицу алгебраических дополнений:
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :
.
Находим матрицу, обратную матрице A , и делаем это легко, так как определитель матрицы A равен единице:
.
Находим неизвестную матрицу:
Пример 5. Решить матричное уравнение
.
Решение. Данное уравнение имеет вид X ⋅ A = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится справа. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A справа. Найдём матрицу, обратную матрице A .
Сначала найдём определитель матрицы A :
.
Найдём алгебраические дополнения матрицы A :
Составим матрицу алгебраических дополнений:
.
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :
.
Находим матрицу, обратную матрице A :
.
Находим неизвестную матрицу:
Пример 6. Решить матричное уравнение
.
Решение. Данное уравнение имеет вид A ⋅ X ⋅ B = C , то есть неизвестная матрица X находится в середине произведения трёх матриц. Поэтому решение следует искать в виде . Найдём матрицу, обратную матрице A .
Сначала найдём определитель матрицы A :
.
Найдём алгебраические дополнения матрицы A :
.
Составим матрицу алгебраических дополнений:
.
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :
.
Находим матрицу, обратную матрице A :
.
Найдём матрицу, обратную матрице B .
Сначала найдём определитель матрицы B :
.
Найдём алгебраические дополнения матрицы B :
Составим матрицу алгебраических дополнений матрицы B :
.
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей B :
.
Находим матрицу, обратную матрице B :
.
📽️ Видео
§28 Матричные уравненияСкачать
§29 Решение матричного уравненияСкачать
Решение системы уравнений методом обратной матрицы - bezbotvyСкачать
Решение системы линейных алгебраических уравнений (СЛАУ) в Excel МАТРИЧНЫМ МЕТОДОМСкачать
2 13 Решение матричного уравнения AXB=CСкачать
Матричное уравнениеСкачать
Решение системы уравнений методом ГауссаСкачать
Обратная матрицаСкачать
Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать
Решение системы уравнений методом обратной матрицы.Скачать
9. Метод обратной матрицы для решения систем линейных уравнений / матричный методСкачать
Линейная алгебра, 7 урок, СЛАУ. Матричный методСкачать
