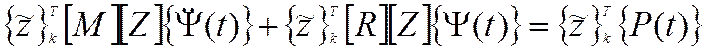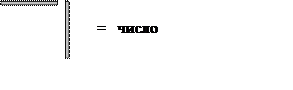| Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 |
1. Ознакомление с приближенным методом матричной итерации для определения собственных форм и частот колебаний упругих конструкций.
2. Ознакомление с экспериментальным методом определения матриц влияния упругих конструкций.
1. Освоение приближенного метода матричной итерации для определения собственных форм и частот колебаний упругих конструкций.
2. Экспериментальное определение матрицы влияния для консоли горизонтального оперения самолета.
3. Расчет при помощи метода матричной итерации первой частоты и формы изгибных колебаний консоли горизонтального оперения самолета.
4. Экспериментальное определение первой частоты изгибных колебаний консоли горизонтального оперения самолета.
5. Сравнение результатов теоретического и экспериментального определения частот изгибных колебаний конструкции горизонтального оперения самолета. Составление выводов.
ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ
Конструкция летательного аппарата является упругодеформируемой и в процессе полета совершает колебательные движения. Она представляет собой динамическую систему с распределенными параметрами жесткости и массы. Рассмотрим в качестве примера консоль крыла самолета, которая в общем случае является балкой переменной изгибной жесткости с переменной погонной массой и нагруженной переменной во времени распределенной нагрузкой q(z, t), где t – время (рис. 4.1).
Рис. 4.1. Схема нагружения консоли
Видео:Матричная форма записи системы линейных уравненийСкачать

Для расчета частот и форм собственных колебаний консоль крыла приводится к системе, состоящей из n материальных точек, имеющих массы mj, каждая из которых является центром масс участка балки длиной Dzj. Эти точки называются узловыми.
Распределенная нагрузка на участке Dzj заменяется эквивалентной сосредоточенной силой Qj:

Прогиб балки при колебаниях можно охарактеризовать перемещениями точек vj(t) вдоль оси y (рис. 4.2). Это говорит о том, что рассматриваемая система имеет n степеней свободы (по числу узловых точек).
Рис. 4.2. Расчетная схема консольной балки
Уравнения колебаний данной системы могут быть получены с использованием коэффициентов влияния для перемещений в узловых точках. Коэффициентом влияния gij называется перемещение i-й точки vi от действия единичной силы Qj = 1, приложенной в j-й точке и совпадающей по направлению с перемещением j-й точки vj. При колебаниях системы на нее будут действовать как внешние силы, так и силы инерции 


Запишем полученное выражение в матричной форме:

где 




Уравнение (4.3) может быть записано в иной форме:

где 
Этим уравнением мы воспользуемся для решения задачи определения собственных форм и частот колебаний системы. Для этого рассмотрим свободные колебания системы, т. е. колебания, которые возникают в системе, не подверженной действию переменных внешних сил (

Допустим, что диссипация энергии в рассматриваемой системе отсутствует. Тогда свободные колебания этой системы будут колебаниями гармоническими. Это значит, что уравнение колебаний (4.5) такой системы допускает решение вида:

где 
w — неизвестная круговая частота колебаний.
Если подставить решение (4.6) в уравнение колебаний (4.5), то получим:

Полученное матричное уравнение представляет собой однородную систему линейных уравнений относительно неизвестных элементов вектора 

Если раскрыть данный определитель, то придем к полиному степени n относительно квадрата круговой частоты w2. Корни этого полинома дадут значения частот w, зная которые, можно найти формы колебаний 
При большом числе степеней свободы удобнее использовать приближенные методы, например, метод матричной итерации. Он позволяет путем последовательных приближений определить основную (низшую) собственную частоту и форму свободных колебаний упругой системы (первый тон).
Суть метода заключается в следующем. Матричное уравнение колебаний системы (4.7) приведем к виду:

введя обозначение: 
Обратим внимание на то, что полученная система уравнений (4.9) имеет такой вид, который допускает для ее решения применение метода последовательных приближений, т. к. искомые элементы вектора 
Далее выбирается произвольная исходная форма 







Матричное уравнение колебаний разобьем на два:


введя некоторый вектор 
Видео:Система линейных уравнений. Метод обратной матрицы. Матричный метод.Скачать

Процесс последовательных приближений построим следующим образом:


Пронормируем вектор 

и подставим в последнее уравнение:

Для выполнения этого равенства должно выполняться условие:


Теперь мы можем получить второе соотношение для последовательных приближений:

Таким образом, последовательность вычислений будет следующая:
1) задаемся произвольно исходной формой, например, в виде:

2) вычисляем 
3) вычисляем 
4) вычисляем 
5) вычисляем 


6) вычисляем частоту

Таким образом, найдены частота w и соответствующая форма колебаний 
Существует теорема, утверждающая, что указанный выше процесс последовательных приближений всегда сходится, причем сходится по частоте и форме колебаний к результату, соответствующему первому тону (т. е. к низшей частоте и соответствующей форме колебаний конструкции) независимо от выбора исходной формы 
Аналогичный процесс последовательных приближений может быть построен и для определения высших (2-го и т. д.) тонов колебаний. Для определения 2-й формы колебаний (и вообще, последующих), необходимо исключить для данной системы возможность колебаний по 1-й форме. Для этого на систему накладывают как бы дополнительную связь и приводят ее к системе с меньшим на единицу числом степеней свободы. Это можно сделать, используя условие ортогональности собственных форм. Для случая изгибных колебаний системы с распределенной массой условие ортогональности имеет вид:

где j и k — номера форм колебаний.
Для системы с сосредоточенными массами данное условие примет вид:

Для исключения первой формы колебаний данное условие для 1-й и 2-й форм запишется в следующем виде:

Исключая из системы уравнений (4.9) одну из амплитуд (например, 

мы придем к системе с меньшим числом степеней свободы, основная частота которой будет совпадать со 2-й частотой первоначальной системы.
Видео:Математика без Ху!ни. Метод Гаусса.Скачать

В матричной форме такое исключение можно записать следующим образом (индекс «(2)» снят):

Матрица 

Матричное уравнение колебаний (4.9) примет вид:


где 
К данному уравнению применим метод матричной итерации и определим с заданной точностью значения амплитуд 



Для определения частот и форм последующих, более высших тонов колебаний общая идея метода остается неизменной, с той лишь разницей, что каждый раз должна строиться новая матрица 
ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ МАТРИЦЫ ВЛИЯНИЯ КОНСОЛИ ГОРИЗОНТАЛЬНОГО ОПЕРЕНИЯ САМОЛЕТА
В настоящей лабораторной работе предлагается расчетным и экспериментальным путем определить частоту и форму низшего тона колебаний консоли горизонтального оперения самолета, установленного на лабораторном стапеле.
Для определения частот и форм указанного тона колебаний конструкции расчетным путем необходимо иметь матрицу гибкости 

Для упрощения решения задачи и сокращения объема работы предлагается выбрать систему с 4-мя точками (n = 4), расположение которых показано на рис. 4.3.
Рис. 4.3. Расчетная схема консоли стабилизатора
Применяемая система измерения перемещений в точках конструкции показана на рис. 4.4.
Рис. 4.4. Схема системы измерения перемещений
На рис. 4.4 показано:
— AB — исходное (до нагружения) положение конструкции;
— CD — жесткая штанга, шарнирно подвешенная к конструкции в точке опоры (предполагается, что последняя абсолютно жесткая в отношении вертикального перемещения и имеет некоторую податливость в отношении углового перемещения) и к концу консоли стабилизатора;
— к штанге против точек i = 1, 2, 3 и 4 прикреплены индикаторы, которые подвижной ножкой упираются в конструкцию оперения;
Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

— AB’ — деформированное положение конструкции;
— CD’ — положение штанги (остается прямолинейной) после деформации стабилизатора;
— BB’ = DD’ = vl — перемещение конца стабилизатора, которое измеряется с помощью нивелира;
— li — показания перемещений по индикаторам в i-х точках.
Для экспериментального определения матрицы гибкости рассматриваемой конструкции необходимо вспомнить физический смысл коэффициентов этой матрицы gij. Напомним, что gij — это перемещение i-й точки от действия единичной силы, приложенной в j-й точке.
Отсюда вытекает следующая методика экспериментального определения элементов матрицы 
1. Рассмотрим точку №1. Приложим в данной точке с координатой z1 последовательно несколько значений силы Q1 и определим перемещения li во всех точках i = 1, 2, 3 и 4 при каждом значении силы. Результаты измерений li занести в табл. 4.1 (всего таких таблиц должно быть четыре — по числу точек приложения силы).
Свойство матрицы жесткости. Произвольное динамическое воздействие. Решение разложением по собственным формам
Страницы работы
Содержание работы
I семестр ЛЕКЦИЯ 10
2.6.3 Свойство матрицы жесткости
Задача о вынужденных колебаниях при гармоническом воздействии сведена к решению алгебраической системы уравнений относительно амплитудных значений обобщенных координат 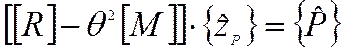
т.е., по сути дела, к решению задачи статики с матрицей жесткости, зависящей от распределения масс и от частоты возмущения.
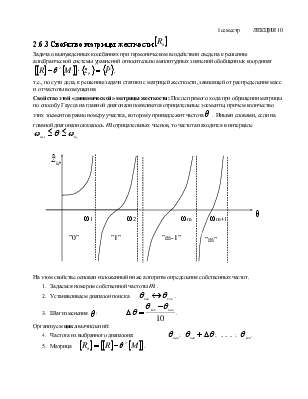
Свойство этой «динамической» матрицы жесткости: После прямого хода при обращении матрицы по способу Гаусса на главной диагонали появляются отрицательные элементы, причем количество этих элементов равно номеру участка, которому принадлежит частота θ . Иными словами, если на главной диагонали оказалось m отрицательных членов, то частота находится в интервале 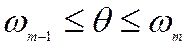
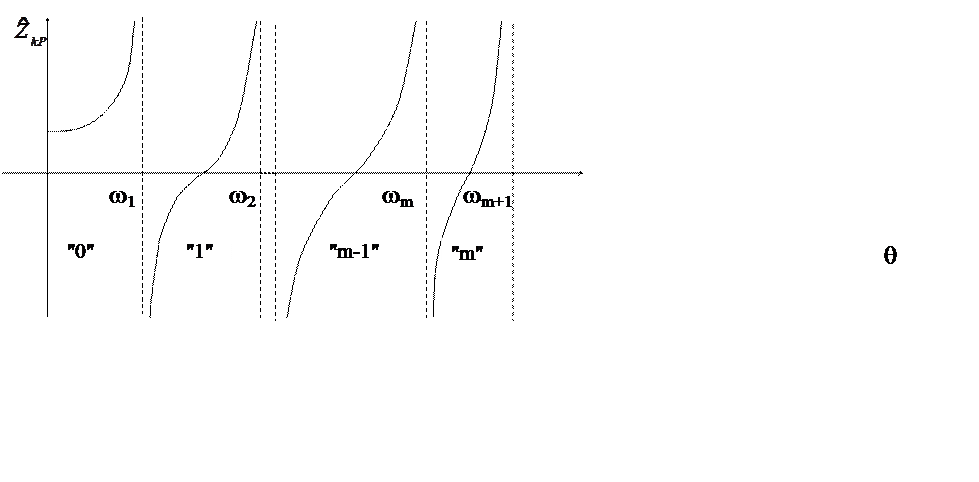 |
На этом свойстве основан изложенный ниже алгоритм определения собственных частот.
- Задаемся номером собственной частоты m .
- Устанавливаем диапазон поиска
.
- Шаг изменения θ:
.
Организуем цикл вычислений:
- Частота из выбранного диапазона:
;
; . . . ;
.
- Матрица
.
- Количество отрицательных членов на главной диагонали матрицы
после прямого хода при обращении матрицы методом Гаусса, равное номеру участка которому принадлежит текущее значение
- Два последовательных значения θm-1и θm, соответствующие участкам m-1 и m, являются нижней и верхней оценками искомой собственной частоты
.
- Если найденный интервал больше заданного заранее значения, т.е.
, то вычисления повторяются , начиная с пункта 3, для нового диапазона
.
Если точность определения собственной частоты достаточна ( условиевыполнено), то после обращения матрицы
вычисляется форма колебаний
.
2.6.4 Произвольное динамическое воздействие. Решение разложением по собственным формам.
Этот способ решения дифференциальных уравнений движения основан на свойстве ортогональности собственных форм.
Как и в задаче о свободных колебаниях начнем с уравнений не содержащих слагаемых, которые описывают диссипативные силы
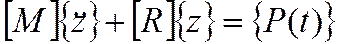
Считая заранее определенными собственные формы колебаний (собственные векторы) динамической системы 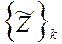
будем искать решение в виде суммы
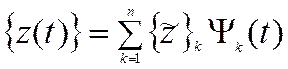
где 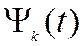
Заметим, что представление решения в виде суперпозиции собственных форм допустимо только для линейных задач.
Видео:МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ период колебаний частота колебанийСкачать

Это же выражение, записанное в матричной форме:
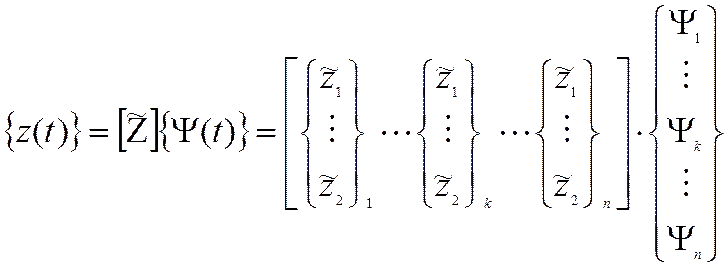
Тогда матричное уравнение движения принимает вид
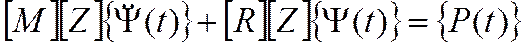
Умножим это уравнение слева на транспонированный столбец 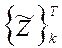
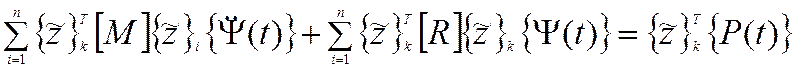
Благодаря свойству ортогональности собственных форм в левой части равенства останутся только слагаемые с i = k, все остальные равны нулю. Следовательно уравнение примет вид
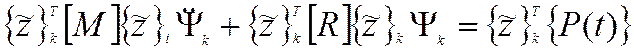
 |
Напомним вид, который приняло уравнение свободных колебаний при подстановке в него частного решения:
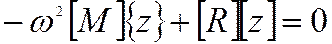
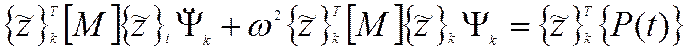
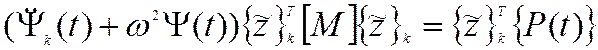
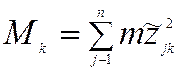
приведенная масса при
колебаниях по k собственной форме
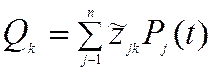
приведенная обобщенная сила при колебаниях по k собственной форме
Уравнение приобретает вид уравнения вынужденных колебаний системы с одной степенью свободы
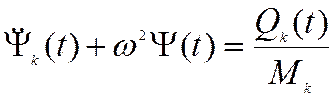
Учтем, что индекс k пробегает значения от 1 доn: k=1,…, n.
Таким образом, благодаря выбору собственных форм в качестве обобщенных координат, получили вместо системы n дифференциальных уравнений относительно n неизвестных функций n отдельных дифференциальных уравнений, каждое из которых определяет одну неизвестную функцию.
Общее решение k—го уравнения есть сумма общего решения соответствующего однородного уравнения и частного решения:
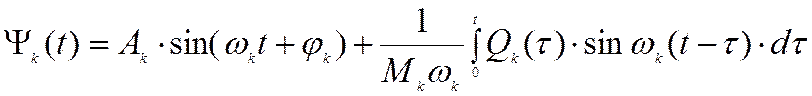
Решением системы уравнений является сумма решений каждого из уравнений
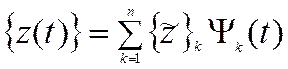
Неизвестные постоянные интегрирования 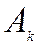
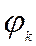
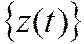
Выше изложен метод главных или нормальных координат, примененный при решении задачи о вынужденных колебаниях системы при отсутствии диссипации.
В связи с отсутствием надежной исходной информации о распределении сил неупругого сопротивления движению, как правило, оказывается достаточным учесть демпфирование на стадии исследования уже преобразованной системы, вводя в каждое из полученных отдельных уравнений слагаемое, пропорциональное скорости. Результатом этого действия станет появление в решении множителя в виде возведенного в отрицательную степень основания натурального алгоритма и изменением значения собственной частоты:
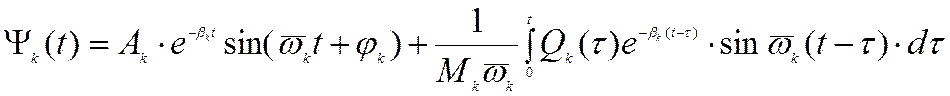
где 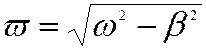
Видео:Решение системы уравнений методом ГауссаСкачать

2.6.5 Произвольное динамическое воздействие. Численное интегрирование.
В тех ситуациях, когда конструкция составлена из разнородных материалов, обладающих резко различными диссипативными свойствами, а также при наличии в системе конструктивных демпферов, введение независимых сил вязкого сопротивления приводит к существенным ошибкам в результатах. Это особенно отчетливо проявляется при близких к резонансным режимах внешних воздействий, причем демпфирование существенно влияет на формы колебаний системы.
В этом случае следует решение производить с помощью численного интегрирования.
Есть и еще один мотив, подталкивающий к использованию процедур численного интегрирования. Когда внешнее воздействие представляет собой сложную функцию времени, и это возмущение задано на ограниченном временном интервале, инженера может интересовать состояние системы в переходных процессах.

Решением является столбец
Весь временной интервал разбивается на малые промежутки 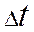
Столбец скоростей 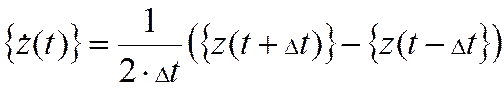
Столбец ускорений 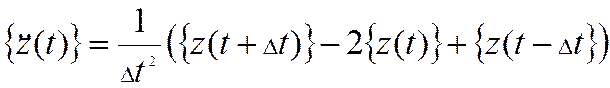
🎬 Видео
Урок 327. Гармонические колебанияСкачать

5.4 Уравнение гармонических колебанийСкачать

Свободные колебания многомассовой системыСкачать

Урок 347. Вынужденные колебания. Резонанс (часть 1)Скачать

Колебания механической системыСкачать

Математические и пружинные маятники. 11 класс.Скачать

Математика это не ИсламСкачать

Свободные колебания одномассовой системыСкачать

Уравнения Лагранжа второго родаСкачать

Колебательное движение. Уравнение гармонических колебаний | ФизикаСкачать

Решение волнового уравнения в три руки под запись на камеру 8000fpsСкачать

Как решить уравнение колебаний? | Олимпиадная физика, механические гармонические колебания, 11 классСкачать

Олегу Тинькову запрещён вход на Мехмат МГУСкачать







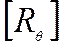
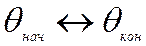 .
.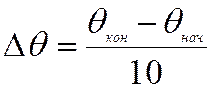 .
.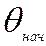 ;
; 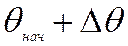 ; . . . ;
; . . . ; 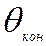 .
.
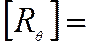
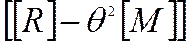 .
.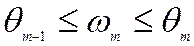 .
.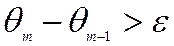 , то вычисления повторяются , начиная с пункта 3, для нового диапазона
, то вычисления повторяются , начиная с пункта 3, для нового диапазона 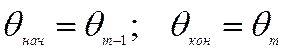 .
. 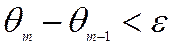 выполнено), то после обращения матрицы
выполнено), то после обращения матрицы 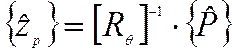 .
.