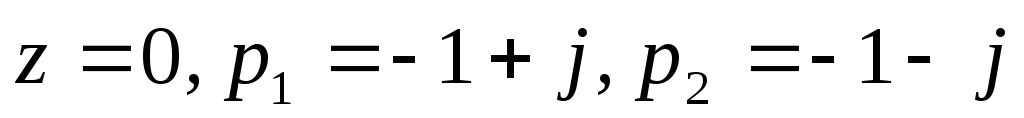Матлаб по точкам найти уравнение (4 видео)

Содержание

Matlab построить график по точкам
Построение графика по узловым точкам
Как найти уравнение графика, соединяющего точки данных в Matlab?
5 ответов
Аппроксимация в Matlab
Аппроксимация
МНК (Метод Наименьших Квадратов)
Примеры задач
💡 Видео

Видео:Решение произвольных уравнений. Методы вычислений в MATLAB. Часть 1. Урок 61Скачать

Matlab построить график по точкам

Видео:Как в MATLAB Simulink моделировать уравнения (Структурная схема САУ)Скачать

Построение графика по узловым точкам

Графики в Matlab, так же как в табличном процессоре, могут быть построены по узловым точкам. Поскольку Matlab — матричная система, совокупность узловых точек у(х) для построения графика задается векторами X и Y одинакового размера.

Графики Matlab строит в отдельных окнах, называемых графическими окнами. С первого взгляда видны отличия графического окна, показанного на рис. 4.5, от командного окна Matlab. В главном меню окна появилась позиция Tools (Инструменты), которая позволяет вывести или скрыть инструментальную панель, видимую в верхней части окна графики на рис. 4.5. Средства этой панели позволяют легко управлять параметрами графиков и наносить на них текстовые комментарии в любом месте.

Рис. 4.5. График, построенный с помощью функции plot

В Matlab для построения графиков функций по узловым точкам в декартовой системе координат служит функция plot. Функция plot имеет несколько синтаксических конструкций:

— plot (X, Y) — строит график функции у(х), координаты точек (х, у) которой берутся из векторов одинакового размера Y и X. Если X или Yматрица, то строится семейство графиков по данным, содержащимся в колонках матрицы;

— plot( Y) — строит график y(i), где значения у берутся из вектора Y, a i представляет собой индекс соответствующего элемента. Если Yсодержит комплексные элементы, то выполняется команда plot (real (Y), imag( Y)). Во всех других случаях мнимая часть данных игнорируется;
— plot(X,Y,S) — аналогична команде plot(X,Y), но тип линии графика можно задавать с помощью строковой константы S.

Значениями константы S могут быть символы, приведенные в табл. 4.5.

Построение графиков в matlab командой plot. Она работает с векторами числовых данных. Синтаксис команды представляет собой: plot (X, Y), где X и Y являются векторами одинаковой длины.

Например вот такой график по точкам matlab:

X = [1 2 3]; Y = [4 6 5]; plot (X, Y)

Рис. 2.5. Построение линейных сегментов

• В этом случае мы отделили несколько команд в одной строке с помощью точки
с запятой, вместо запятой. Обратите внимание, что вывод команд,
предшествующих знаку точка с запятой, запрещается.

Команда plot рассматривает вектора X и Y, как перечни координат
последовательных точек на графике, и соединяет точки в виде линейных
сегментов. Таким образом, на Рис. 2.5 показано, как программа MATLAB
соединяет точки с координатами (1, 4), (2, 6) и (3, 5).

Чтобы начертить графики функций matlab например х 2 в интервале от -1 до 2, сначала требуется создать перечень X из значений х, а затем ввести plot (X, Х.^2). (Точка в
данном выражении обязательна, так как Х.^2 представляет собой
поэлементное возведение в квадрат вектора X, но не матричный квадрат.) Нам
необходимо использовать достаточное количество значений х для уверенности в
том, что результирующий график, нарисованный путем соединения точек,
будет выглядеть нормально (плавная, а не ломаная линия). Мы используем
приращение в размере 0.01. Таким образом, чтобы отобразить график
параболы, введите:

X = -1:0.01:2; plot(X, X.^2)

Результат отображен на Рис. 2.6. Обратите внимание, что мы использовали точку
с запятой, чтобы запретить вывод вектора X из 301 элемента.

Рис. 2.6. Построенная парабола

Более подробно графические команды программы MA TLAB рассматриваются в уроке 5.
А пока удовлетворимся демонстрацией построения пары выражений на одном и
том же графике. Надеюсь теперь вы получили подробный ответ на свой вопрос: как строить графики в matlab.

Поэтому из выше всего сказанного можно сделать вывод, что вам необходимо просмотреть много дополнительной информации и альтернатив!

MATLABимеет исключительно мощную систему для построения различных двухмерных и трехмерных графиков, а также их настройки, редактирования и форматирования. Типы и подтипы графиковMATLABочень разнообразны. Список функций двумерной графики можно получить командойhelp graph2d, трехмерной –help graph3d.

Графики выводятся в отдельных графических окнах с помощью команды вида figure(n), гдеn – номер графического окна. На одном графике можно построить несколько кривых, отличающихся цветом и типами линий и точек. Графики могут быть скопированы и вставлены в другие приложения:Word,Excel,PowerPointи др. Для этого используется командаEdit/ Copy Figureокна графики.

Часто используемые команды при построении графиков

plot(t,y) % График непрерывной функции y(t)

plot(x1, y1, x2, y2) % Графики зависимостей y1 от x1 и y2 от x1

stem(x,y) %График дискретной функции (сигнала)y(x)

stairs(x,y) % График в виде ступенчатой линии

loglog(f,Y) %График с логарифмическими масштабами по x и y

semilogx(f,Y) %Логарифмический масштаб поxи линейный поy

polar(phi,r) % График в полярных координатах

title(‘ название’) % Вывод заголовка графика

xlabel(‘время’) % Метка по осиx

ylabel(‘Напряжение’) % Метка по осиy

legend(‘АЧХ системы‘) % Вывод поясняющей надписи

axis([xmin, xmax, ymin, ymax]) % Установка масштабов по осямxи y

xlim([xmin,xmax]) % Установка масштаба по осиx

ylim([ymin,ymax]) % Установка масштаба по осиy

figure(n) % Устанавливает фигуру (окно)nактивной

subplot(r,c,n) % Разбивает графическое окно наr * cподокон иsubplot(rcn) % устанавливает подокноn в качестве активного.

gridon% к графику добавляется сетка

holdon% позволяет построить несколько графиков в окне

holdoff% отменяетholdonдля текущего графика

text% позволяет разместить текст на графике

zoomon/off% включение / выключение возможности увеличения % фрагментов графика с использованием

% левой и правой кнопок мыши

Построение графика зависимости функции yот индекса массива (номера элемента)x

Построение графика зависимости y(x)

Несколько пар аргументов в функции plot()позволяют построить несколько графиков в одном графическом окне. При этомMATLABдля каждого графика использует отдельный цвет линии.

Цвет, тип линии и обозначение (тип) точек являются аргументами функции plot, соответствующие справочные сведения можно получить с помощью команды вызова справкиhelp plot .

Для разбиения графического окна на подокна служит команда plot(m,n,p)илиplot(mnp),в которойm– число строк,n— число столбцов,p— номер подокна. Пример построения графика функции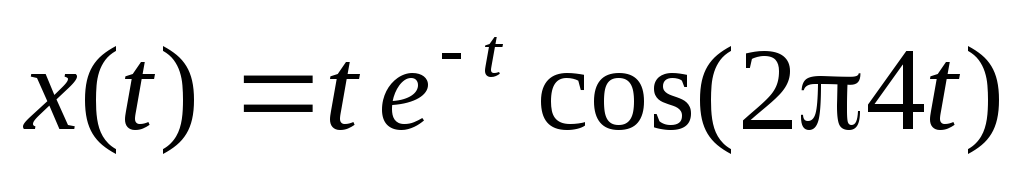в двух подокнах с помощью функцииplot()в одном случае и функцииstem()в другом с разными пределами по оси аргумента (рис. 7):

t=linspace(0, 8, 401); % вычисление 402 точек в интервале [0,8]

axis([0 1 min(x) max(x)] )

Fs=1024; % Частота отсчетов

f1=50; % частота гармоники

N=512; % число отсчетов сигнала

t=0:1/Fs:(N-1)/Fs; % вектор времени

plot(t,x), grid % график сигнала

Для добавления графиков к уже существующим применяют команду hold on

Для отмены действия hold on (освобождения окна графики) используют hold off.

Пример построения графика в полярной системе координат

В окне графики MATLABпозволяют выполнять разнообразную настройку графического окна и его объектов с помощью меню или панели инструментов (рис.9).

В окне редактора или с помощью контекстного меню по правой кнопке мыши производятся необходимые установки (цвет, размер, тип, толщина линии и др.) объекта окна графики.

Возможности для подобной интерактивной настройки графики — очень широкие. В первую очередь они обеспечиваются кнопкой Edit Plot инструментальной панели окна.

Трехмерная графика MATLAB– очень развитая и многообразная, сама по себе очень важная часть программы, но в курсе «Сигналы и системы» она используется редко.

Некоторые из команд построения 3D– графиков

>> plot3(…) % строит аксонометрическое изображение 3D-поверхности

>> mesh(…) % строит трехмерные поверхности со специфицированной

Пример построения графика передаточной функции системы второго порядка с передаточной функцией .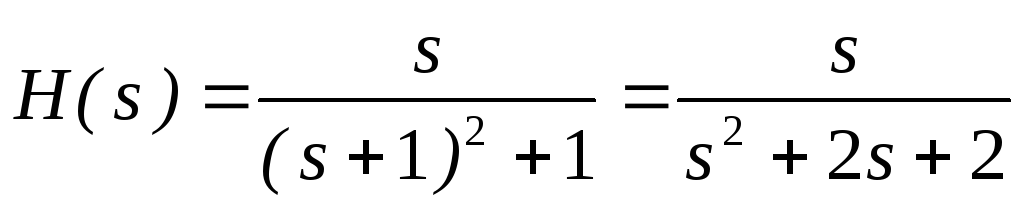

Нули и полюса системы :

Видео:Составляем уравнение прямой по точкамСкачать

Как найти уравнение графика, соединяющего точки данных в Matlab?

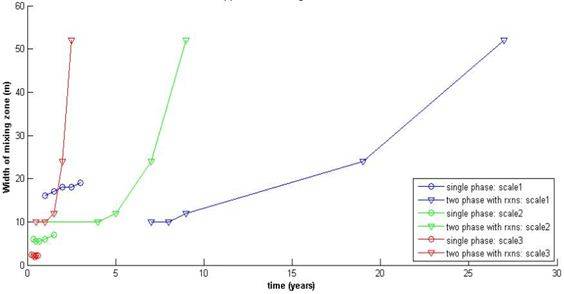
У меня есть различные сюжеты (с hold on ), как показано на следующем рисунке:

Я хотел бы знать, как найти уравнения этих шести кривых в Matlab. Спасибо.

Видео:ТАУ. Matlab/SIMULINK Фазовые портреты систем нелинейных диф. уравненийСкачать

5 ответов

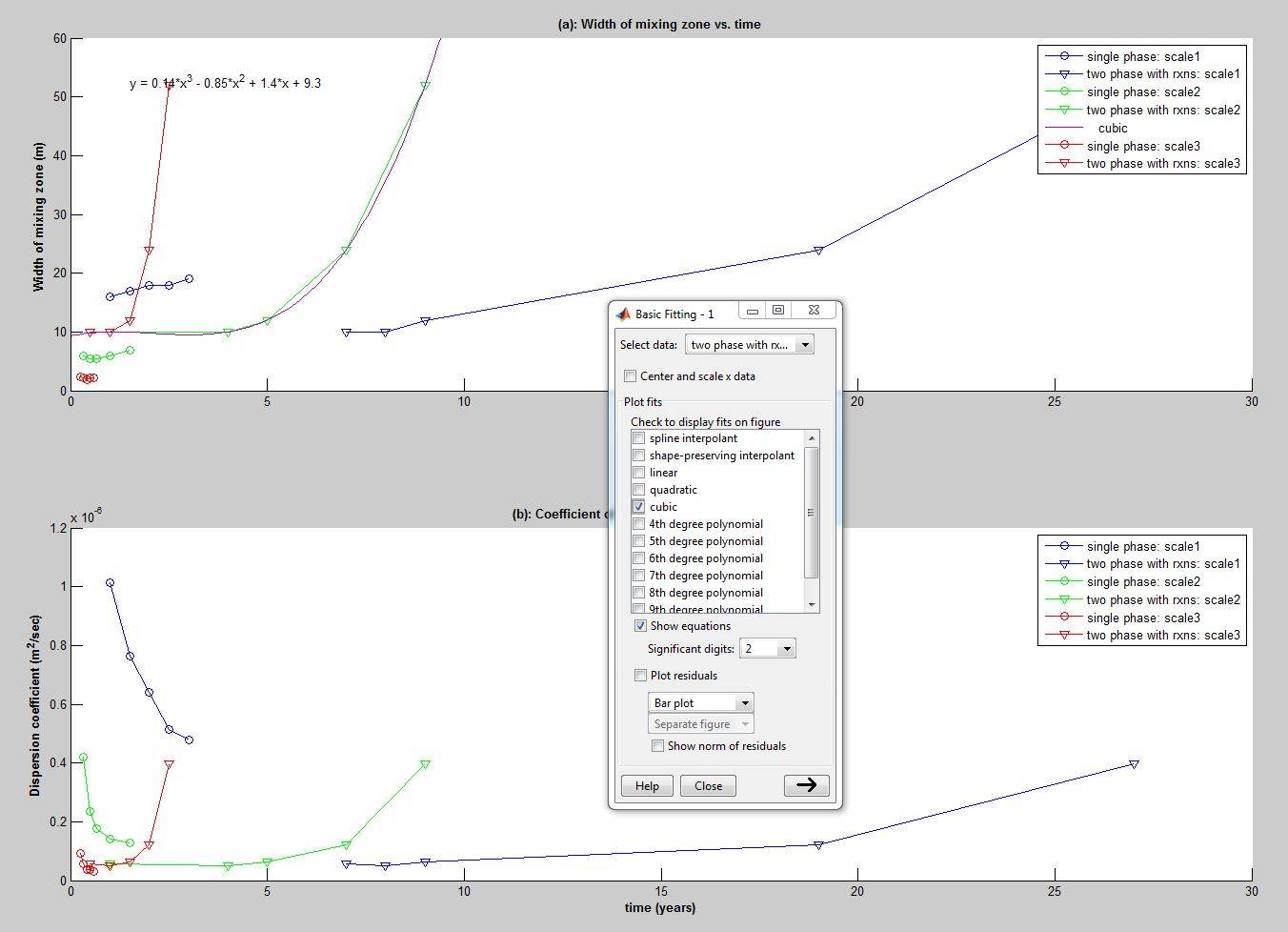
нашел интерактивный инструмент установки в Matlab простой и полезный, хотя несколько ограниченный по объему:

график выше кажется линейной интерполяцией. Учитывая векторы X и Y данных, где X содержит аргументы, а Y-точки функции, вы можете сделать

чтобы получить линейно интерполированное значение f (x). Например, если данные

должно дать вам очень грубое приближение к 1.5^2 . interp1 будет точно соответствовать графику, но вас могут заинтересовать более причудливые операции подгонки кривых, такие как сплайн приближений и т. д.

тут rxns подставка для реакции? В этом случае, ваши кривые, скорее всего, экспоненциальный. Экспоненциальная функция имеет вид: y = a*exp(b * x) . В твоем случае, y — ширина зоны смешивания и x — это время в годах. Теперь, все, что вам нужно сделать, это запустить экспоненциальная регрессия в Matlab найти оптимальные значения параметров a и b , и у вас будут свои уравнения.

совет, хотя может быть лучший ответ, от меня: попробуйте увидеть скорость увеличения кривой. Например, кубический является более репрезентативным, чем квадратичный, если скорость увеличения кажется быстрой и найти полином и вычислить ошибку отклонения. Для нерегулярных кривых, вы можете попробовать сплайн сторона. Я думаю, что в matlab также есть набор инструментов для сплайн-фитинга.

существует способ извлечения информации с помощью текущего дескриптора фигуры (gcf) из вашего графика.

например, вы можете получить ряд, который был нанесен на график:

должна быть другая информация, которую вы можете получить от » findall(gcf. )» методы.

Видео:ТАУ. Matlab/SIMULINK Фазовые портреты нелинейных и линейных диф. уравненийСкачать

Аппроксимация в Matlab

Приветствую! Сегодня продолжаем говорить об обработке экспериментальных данных. Сегодняшняя статья — продолжение предыдущей темы: Интерполяция в Matlab. Настоятельно советую с ней ознакомиться перед чтением данной статьи. По сути аппроксимация в Matlab очень похожа на интерполяцию, однако, для её реализации используются другие правила и функции.

Видео:MatLab. 6.1. Решение уравненийСкачать

Аппроксимация

Относительно интерполяции, аппроксимация получила более широкое распространение. Сущность этого метода состоит в том, что табличные данные аппроксимируют кривой, которая не обязательно должна пройти через все узловые точки, а должна как бы сгладить все случайные помехи табличной функции.

МНК (Метод Наименьших Квадратов)

Одним из самых популярных методов аппроксимации в Matlab и в других средах, это Метод Наименьших Квадратов ( МНК ). В этом методе при сглаживании опытных данных аппроксимирующую кривую стремятся провести так, чтобы её отклонения от табличных данных по всем узловым точкам были минимальными.

Суть МНК заключается в следующем: для табличных данных, полученных в результате эксперимента, отыскать аналитическую зависимость, сумма квадратов уклонений которой от табличных данных во всех узловых точках была бы минимальной.

Аппроксимация в Matlab по МНК осуществляется с помощью функции polyfit. Функция p = polyfit(x, y, n) находит коэффициенты полинома p(x) степени n, который аппроксимирует функцию y(x) в смысле метода наименьших квадратов. Выходом является строка p длины n+1, содержащая коэффициенты аппроксимирующего полинома.

Примеры задач

Разберём задачу, в которой разрешается использование встроенных матлабовских функций.

Осуществить аппроксимацию в Matlab табличных данных x = [0, 0.1 , 0.2, 0.3, 0.5] и y = [3, 4.5, 1.7, 0.7, -1] . Применяя метод наименьших квадратов, приблизить ее многочленами 1-ой и 2-ой степени. Для каждого определить величину среднеквадратической ошибки. Построить (на одном листе) графики и заданной таблично функции (ломанная линия) и приближающих ее многочленов 1-ой и 2-ой степени.

Вывод:
ans = 0.9253
ans = 0.8973

Однако, встречаются задачи, где требуется реализовать аппроксимацию в Matlab без использования специальных функций.

Найти у(0.25) путём построения аппроксимирующего полинома методом наименьших квадратов согласно данным:
x: 0, 0.1, 0.2, 0.3, 0.5
y: 3, 4.5, 1.7, 0.7, -1
p: 0.5, 0.8, 1.6, 0.8, 0.1
Построить этот полином без учёта весовых коэффициентов с использованием определителя Вандермонда и стандартных операторов.

Вывод:
a =
228.1447
-176.0984
22.7745
3.1590
qq = 228.1447 -176.0984 22.7745 3.1590
y2 = 1.4113

Как видите встроенные функции для аппроксимации в Matlab укорачивают алгоритм почти вдвое.

Существует также возможность реализации всего алгоритма через одну функцию, но для преподавателей студентов она скорее всего будет не приемлема. С помощью функции lsqcurvefit(fun,x0,xdata,ydata), где:
xdata,ydata– табличные значения аппроксимируемой функции;
x0 –стартовое значение параметров функции;
fun – функция аппроксимации, задаваемая пользователем

С аналитически-теоретической стороны, существуют такие виды аппроксимации: