Материальный и энергетический балансы потока уравнение бернулли и уравнение неразрывности потока (4 видео)

Содержание

Материальный и энергетический балансы потока уравнение бернулли и уравнение неразрывности потока
Уравнение неразрывности
Уравнения Бернулли
Уравнение неразрывности и уравнение Бернулли.
Уравнение неразрывности потока жидкости
Уравнение неразрывности струи жидкости. Уравнение Бернулли.
Видео по теме уравнение неразрывности
🎬 Видео

Видео:Физика. 10 класс. Уравнение неразрывности. Уравнение Бернулли. Подъёмная сила /29.10.2020/Скачать

Материальный и энергетический балансы потока уравнение бернулли и уравнение неразрывности потока

1.4. Характеристики движения жидкостей. Уравнение неразрывности. Уравнение Бернулли, примеры его приложения

Характеристики движения жидкостей.

Течение жидкости может быть неустановившимся (нестационарным) или установившимся (стационарным).

Неустановившееся движение – такое, при котором в любой точке потока скорость движения и давление с течением времени изменяются, т.е. w и P зависят не только от координат точки в потоке, но и от момента времени, в который определяются характеристики движения.

Примером неустановившегося движения может являться вытекание жидкости из опорожняющегося сосуда, при котором уровень жидкости в сосуде постепенно меняется (уменьшается) по мере вытекания жидкости.

Установившееся движение – такое, при котором в любой точке потока скорость движения и давление с течением времени не изменяются, т.е. w и P зависят только от координат точки в потоке, но не зависят от момента времени, в который определяются характеристики движения.

Пример установившегося движения — вытекание жидкости из сосуда с постоянным уровнем, который не меняется (остаётся постоянным) по мере вытекания жидкости.

В случае установившегося течения в процессе движения любая частица, попадая в заданное, относительно твёрдых стенок, место потока, всегда имеет одинаковые параметры движения. Следовательно, каждая частица движется по определённой траектории.

Траекторией называется путь, проходимый данной частицей жидкости в пространстве за определенный промежуток времени.

При установившемся движении форма траекторий не изменяется во время движения. В случае неустановившегося движения величины направления и скорости движения любой частицы жидкости непрерывно изменяются, следовательно, и траектории движения частиц в этом случае также постоянно изменяются во времени.

Поэтому для рассмотрения картины движения, образующейся в каждый момент времени, применяется понятие линии тока.

Линия тока— это кривая, проведенная в движущейся жидкости в данный момент времени так, что в каждой точке векторы скорости w_i совпадают с касательными к этой кривой.

Нужно различать траекторию и линию тока. Траектория характеризует путь, проходимый одной определенной частицей, а линия тока направление движения в данный момент времени каждой частицы жидкости, лежащей на ней.

При установившемся движении линии тока совпадают с траекториями частиц жидкости. При неустановившемся движении они не совпадают, и каждая частица жидкости лишь один момент времени находится на линии тока, которая сама существует лишь в это мгновение. В следующий момент возникают другие линии тока, на которых будут располагаться другие частицы.

Установившееся движение подразделяется на равномерное и неравномерное.

Равномерное движение характеризуется тем, что скорости, форма и площадь сечения потока не изменяются по длине потока. Неравномерное движение отличается изменением скоростей, глубин, площадей сечений потока по длине потока.

Уравнение неразрывности

Скорость движения частиц жидкости неодинаковы по сечению ее потока. Поэтому вводится понятие о средней скорости потока всех частиц жидкости в сечении.

Допустим, что в сечении I-I трубы (рис. а) все частицы имеют среднюю скорость w, тогда за единицу времени они пройдут путь, равный w, и переместятся в сечение II-II. Объем жидкости, протекающей в ед. времени через сечение I-I , будет равен V, заключенному между сечениями I-I и II-II, т.е. произведению средней скорости w на площадь поперечного сечения S потока.

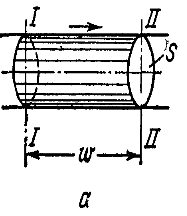
Это произведение представляет собой объемный расход жидкости:

V=wS [м 3 /с] – уравнение расхода, где w-линейная скорость (путь, проходимый жидкостью в ед. времени)

Массовая скорость W представляет собой количество жидкости, протекающее через ед. поперечного сечения потока, в ед. времени, и определяется из соотношения:

W=G/S [кг/м 2 с] где G – массовый расход жидкости [кг/c]

W=wρ – зависимость м/д массовой и линейной скоростью.

Если скорость частиц жидкости не изменяются во времени, ее движение считается установившимся. При установившемся движении в каждом сечении потока постоянны не только скорость, но и расход, температура, давление и плотность жидкости. Вместе с тем при установившемся движении скорости потока могут изменяться в пространстве, при переходе жидкости от одного сечения к другому.

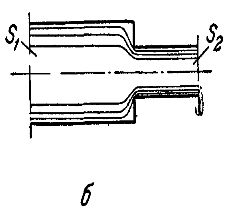
Рассмотрим установившееся движение жидкости, ограниченной стенками любой формы, например движение в трубе переменного сечения (рис. б). Движущаяся жидкость сплошь заполняет трубу, в которой, таким образом, нет пустот и разрывов потока. При переходе от сечения S₁ к сечению S₂ скорость жидкости будет изменяться, но по закону сохранения ве-ва кол-во жидкости, поступающей в ед. времени через сечение S₁, будет равно кол-ву ее, протекающему через сечение S₂, т.е. расход жидкости останется постоянным. В том случае, если эти кол-ва не были бы равны, жидкость накапливалась бы в трубе, м/д сечениями S₁ и S₂, и здесь происходило бы возрастание ее плотности и давления, что при установившемся движении невозможно.

Принимая массовые скорости жидкости в сечениях S₁ и S₂ равным соответственно W₁ и W₂, можно написать

где ρ_1, ρ₂-плотность жидкости в сечениях S₁ и S_2.

Для несжимаемой жидкости ρ₁=ρ₂ и уравнение принимает вид

Данное уравнение представляет собой материальный баланс потока жидкости и называются уравнение неразрывности потока.

Согласно этим уравнениям, средние скорости жидкости в различных сечениях трубопровода обратно пропорциональны площадям этих сечений. Произведение скорости на сечение, т.е. расход жидкости при установившемся движении, есть величина постоянная.

Уравнение Бернулли, примеры его приложения.

При движении по трубопроводу без дополнительного подвода энергии или ее отвода удельная энергия жидкости, по закону сохранения энергии, не будет изменяться. Поэтому при перемещении жидкости от некоторого сечения I-I до сечения II-II удельные энергии жидкости в этих сечениях будут одинаковы:

u – внутренняя энергия, v – скорость.

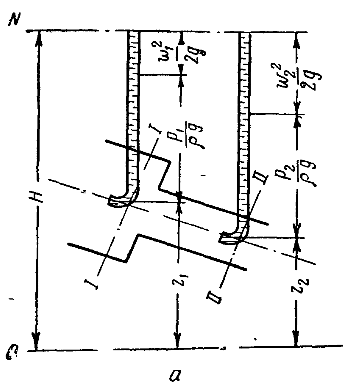
Уравнение, выражающее энергетический баланс движущейся идеальной жидкости (рис. а):

z – потенциальная энергия положения жидкости – геометрический напор

p/ρg – потенциальная энергия давления жидкости [м] — скоростной напор

может быть измерена вертикальной пьезометрической трубки, под действием давления жидкость поднимается на высоту h= p/ρg, которая называется пьезометрическим (статическим) напором.

w 2 /2g – удельная кинетическая энергия движущейся жидкости [м]

При движении идеальной жидкости сумма геометрического, пьезометрического и скоростного напоров во всех сечениях потока явлю постоянной величиной.

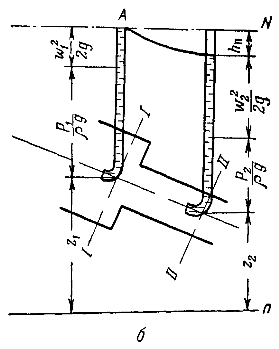
Для реальной жидкости, при переходе от сечения I-I до сечения II-II (рис. б) часть удельной энергии будет расходоваться на преодоление трения и др. сопротивлений. Потерянная энергия превращается в тепло, вследствие чего увеличивается внутренняя энергия жидкости (при отсутсв. обмена с окруж. средой):

При установившемся движении реальной жидкости сумма геометрического, пьезометрического, скоростного и потерянного напора в каждой точке любого сечения потока является постоянной величиной.

Сумма геометрического, пьезометрического, скоростного напоров называется гидродинамическим напором.

Гидродинамический напор реальной жидкости уменьшается в направлении ее движения на величину напора, потерянного между начальным и конечным сечениями потока.

Пользуясь уравнением Бернулли, определяют скорость и расход жидкости, т.е. пропускную способность аппаратов и трубопроводов. При помощи этого ур-я рассчитывают также время истечения жидкости и ее полный напор.

Видео:Урок 132. Основные понятия гидродинамики. Уравнение непрерывностиСкачать

Уравнение неразрывности

Уравнение неразрывности движения жидкости представляет собой закон сохранения массы изолированной системы. В общем виде:

где — дивергенция вектора скорости, т. е. относительное изменение объема с течением времени, р — плотность.

В случае, когда жидкость является несжимаемой (dpi dt = 0), уравнение (1.32) упрощается:

Элементарный расход жидкости при установившемся движении есть величина постоянная для всей элементарной струйки.

Уравнение неразрывности для потока жидкости: расход жидкости через любое сечение потока при установившемся движении есть величина постоянная.

Видео:Урок 133. Закон Бернулли. Уравнение БернуллиСкачать

Уравнения Бернулли

Уравнение Даниила Бернулли, полученное в 1738 г., является фундаментальным уравнением гидродинамики и выражает закон сохранения энергии движущейся жидкости. Уравнение Бернулли определяет применение этого закона к установившемуся одномерному потоку несжимаемой жидкости. Индексами (1) и (2) обозначены величины, соответственно относящиеся к сечению потока 1—1, взятому выше по течению, и к сечению 2-2, взятому ниже по течению (рис. 1.11-1.13).

Уравнением Бернулли для элементарной струйки идеальной (невязкой) жидкости называется следующее выражение:

где и — скорость движения жидкости в поперечном сечении элементарной струйки, Н — гидродинамический напор, равный полной энергии потока Е (рис. 1.12).

Для реальной (вязкой) жидкости напор в любом вышележащем сечении всегда будет больше напора в нижележащем по течению сечении, т. к. часть энергии затрачивается на преодоление сил сопротивления (рис. 1.13), т. е. можно записать уравнение Бернулли для элементарной струйки реальной (вязкой) жидкости в следующем виде:

где — удельные потери напора на преодоление всех сопротивлений (преодоление сил вязкости и сил трения между жидкостью и стенкой).

Рис. 1.12. К уравнению Бернулли для струйки невязкой жидкости [38]

Для решения задач практической гидравлики выбирают два сечения по длине потока так, чтобы для одного из них были известны величины z,p и v, а для другого одна или две подлежали определению.

Рис. 1.13. К уравнению Бернулли для струйки вязкой жидкости (штриховкой показаны потери напора по пути движения) [38]

При переходе от элементарной струйки к потоку вязкой жидкости, имеющему конечные размеры, необходимо учесть неравномерность распределения скоростей в живых сечениях и иметь представление о случаях возможного и невозможного применения уравнения Бернулли.

Решение этих вопросов сводится к установлению поправочных коэффициентов и выделению потоков с плавно изменяющимся движением, т. е. таким движением, при котором угол расхождения между соседними элементарными струйками настолько мал, что составляющими скорости в поперечном сечении можно пренебречь.

При движении вязкой жидкости вдоль твердой стенки ее скорость достигает максимального значения в центральной части потока и уменьшается до нуля возле стенки. Неравномерное распределение скоростей означает неодинаковое скольжение одних элементарных струек по другим, движение вязкой жидкости сопровождается вращением частиц, вих- реобразованием и перемешиванием. Поэтому, приходится вводить среднюю по сечению скорость v. Для приведения результатов расчетов по средней скорости в соответствие с действительными скоростями вводится коэффициент Кориолиса а, характеризующий неравномерное распределение скоростей в живом сечении потока, представляющий собой отношение кинетической энергии, подсчитанной по истинным скоростям сечения, к той же энергии, вычисленной по средней скорости в этом же сечении потока. Обычно в трубопроводах и каналах а = 1,05. 1,1, иногда приближенно принимают а = 1.

Рис. 1.14. К уравнению Бернулли для потока вязкой жидкости [32]

Поэтому уравнение Бернулли для потока вязкой жидкости (рис. 1.14) с учетом неравномерности распределения скоростей по живому сечению запишется следующим образом:

где zi, z₂ — геометрический напор или геометрическая высота положения центра тяжести живого сечения потока над произвольно взятой горизонтальной плоскостью сравнения — высота давления,

пьезометрическая высота, т. е. высота такого столба жидкости, который соответствует гидродинамическому давлению в центре тяжести

живого сечения потока; — скоростной напор или скоростная

высота; h_w — потерянный напор; а — коэффициент Кориолиса, характеризующий неравномерное распределение скоростей в живом сечении потока; vi, V2 — средняя скорость в 1 и 2 живом сечении соответственно.

Уравнение Бернулли устанавливает связь между высотными положениями частиц жидкости, давлением и скоростями в разных сечениях потока жидкости. Причем каждая из входящих в уравнение величин может изменяться, но сумма остается постоянной.

Видео:Закон БернуллиСкачать

Уравнение неразрывности и уравнение Бернулли.

Уравнение неразрывности потока и уравнения Бернулли являются основными уравнениями гидродинамики. При изучении потоков жидкости вводится ряд понятий, характеризующий потоки с гидравлической и геометрической точек зрения.

Такими понятиями являются: площадь живого сечения потока(или живое сечение потока), расход и средняя скорость.

Площадью живого сечения потока, называют площадь сечения потока, приведенную нормально к направлению линии тока, т.е. перпендикулярно движению струйки жидкости. Живое сечение может быть ограничено твердыми стенками полностью или частично. Если стенки ограничивают поток полностью, то движение жидкости называют напорным; Если же ограничение частичное, то движение называется безнапорным.

Напорное движение характеризуется тем, что гидродинамическое давление в любой точке потока отлично от атмосферного и может быть как больше, так и меньше него. Безнапорное движение характеризуется постоянным давлением на свободной поверхности, обычно равным атмосферному.

Содержание статьи

Расходом потока называется количество жидкости, протекающей через поперечное сечение в единицу времени. Если рассматривать поток жидкости, представляющий собой совокупность большого числа элементарных струек, то очевидно, общий расход жидкости для всего потока в целом представляет собой сумму расходов всех отдельных струек.

Для нахождения этой суммы необходимо знать закон распределения скоростей в сечении потока. Так как во многих случаях движения такой закон неизвестен, в общем случае суммирование становится невозможным. Поэтому в гидродинамике вводится предположение, что все частицы жидкости по всему поперечному сечению потока движутся с одинаковой скоростью. Эту воображаемую фиктивную скорость называют средней скоростью потока υ_ср .

Таким образом уравнение расхода для потока будет

υ_ср – средняя скорость потока

F – площадь сечения потока.

Видео:Уравнение Бернулли для потока жидкостиСкачать

Уравнение неразрывности потока жидкости

Теперь вооружившись основными понятиями перейдем к определению уравнения неразрывности потока.

Отделим сечениями 1-1 и 2-2 некоторый отрезок элементарной струйки. В этот отрезок в единицу времени через сечение 1-1 втекает объем жидкости равный

а через сечение 2-2 из него же вытекает объем, равный

Примем, что жидкость несжимаема и что в ней невозможно образование незаполненных жидкостью пространств – т.е. будем считать, что соблюдается условие сплошности или неразрывности движения.

Учитывая, что форма элементарной струйки с течением времени не изменяется и поперечный приток в струйку или отток из ней отсутствуют, приходим к выводу, что элементарные расходы жидкости, проходящие через сечение 1-1 и 2-2, должны быть одинаковы.

Такие соотношения можно составить для любых двух сечений струйки. Поэтому в более общем виде получаем, что всюду вдоль струйки

Это уравнение называется уравнением неразрывности жидкости – оно является первым основным уравнением гидродинамики. Переходя далее к потоку жидкости в целом получаем, что

т.е. средние скорости в поперечных сечениях потока при неразрывности движения обратно пропорциональны площади этих сечений.

Уравнение неразрывности струи жидкости. Уравнение Бернулли.

Вторым основным уравнением гидродинамики является уравнение Бернулли, устанавливающее взаимосвязь между скоростью и давлением в различных сечениях одной и той же струйки.

При рассмотрении уравнения Бернулли также как и в предыдущем случае ограничимся установившемся медленно изменяющимся движением. Выделим в объеме некоторой жидкости одну элементарную струйку и ограничим её в какой-то определенный момент времени Т сечениями 1-1 и 2-2.

Допустим, что через какой-то промежуток времени ΔТ указанный объем переместится в положение 1’ – 1’ и 2’ – 2’. Тогда применяя к движению этого сечению теорему кинетической энергии, определяем, что приращение кинетической энергии движущейся системы материальных частиц равняется сумме работ всех сил, действующих на систему.

Если всё это записать в виде формулы, то

где W – приращение кинетической энергии = m * υ 2 / 2

ΣA – сумма работ действующих сил = P *ΔS

В этих выражениях
m – масса
υ – скорость материальной точки
P – равнодействующая всех сил, приложенных к точке,
ΔS – проекция перемещения точки на направление силы.

Теперь рассмотрим обе части этого выражения по порядку.

Приращение кинетической энергии ΔW

В нашем случае приращение кинетической энергии определяется как разность значений кинетической энергии в двух положениях перемещающегося объема, т.е. как разность кинетической энергии объема образованного сечениями 1-1’ и объема, образованного сечениями 2 – 2’.

Эти объемы являются результатом перемещения за время ΔТ сечений выделенного участка элементарной струйки.

Вспоминая, что по условию неразрывности расход во всех сечениях элементарной струйки одинаков, а следовательно будет равен

масса в этом случае получается равной

Подставляя все это в выражение для кинетической энергии получаем цепочку

ΔW = m * υ 2 ₂ / 2 — m * υ 2 ₁ / 2 = ρ * q * ΔТ * υ 2 ₂ / 2 — ρ * q * ΔТ * υ 2 ₁ / 2

Работа сил действующих на систему ΣA

Теперь перейдем к рассмотрению работы сил, действующих на рассматриваемый объем жидкости. Работа сил тяжести A_Т равна произведению этой силы на путь, пройденный центром массы движущегося объема жидкости по вертикали.

Для рассматриваемой в нашем примере струйки работа сил тяжести будет равна произведению сил тяжести объема занимаемого сечениями 1-1’ и 2 – 2’ на расстояние Z1 –Z2.

Где Z1 и Z2 – расстояния по вертикали от горизонтальной плоскости, называемой плоскостью сравнения до центров масс объемов 1-1’ и 2 – 2’.

Силы давления А_Д , действующие на объем жидкости складываются из сил давления на его боковую поверхность и на концевые поперечные сечения. Работа сил давления на боковую поверхность равна нулю, так как эти силы за все время движения нормальны к перемещению их точек приложения.

Суммарно работа сил давления будет

Подставляя в начальное уравнение

Полученные выражения для ΔW и ΣA получаем

Разделим обе части этого уравнения на m = ρ*q*ΔТ и перегруппируем слагаемые

Учитывая, что сечения 1-1 и 2-2 взяты нами совершенно произвольным образом, это уравнение возможно распространить на всю струйку. Применив его для любых поперечных сечений, взятых по её длине, и представить в общем виде:

Записанные выше два уравнения представляют собой уравнение Бернулли для элементарной струйки жидкости. Сумма трех слагаемых, входящих в это уравнение, называется удельной энергией жидкости в данном сечении струйки. Различают такие энергии как:
Удельная энергия положения = qz
Удельная энергия давления = p/ ρ
Кинетическая удельная энергия = υ 2 / 2

В соответствии с этим уравнение Бернулли для струйки жидкости можно сформулировать следующим образом: для элементарной струйки идеальной жидкости полная удельная энергия, т.е. сумма удельной энергии положения, удельной энергии давления и кинетической удельной энергии – есть величина постоянная во всех сечениях струйки.

Видео по теме уравнение неразрывности

Полученные в результате многочисленных экспериментов данные из уравнения Бернулли и уравнения неразрывности потока жидкости нашли широкое применение в повседневной жизни.

Уравнение Бернулли широко используется для нахождения скорости истечения жидкости через отверстия.

Уравнение неразрывности обладает широкой универсальностью и справедливо для любой сплошной среды. Принцип уравнения неразрывности используется для формирования сильной и дальнобойной струи воды при тушении пожаров.