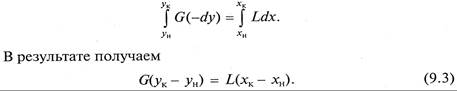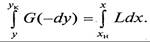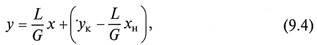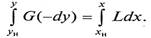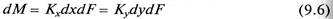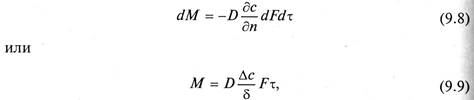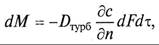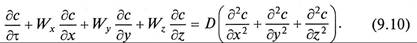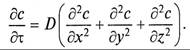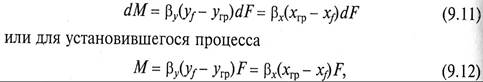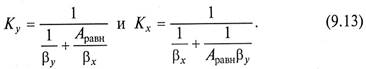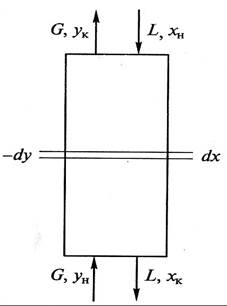
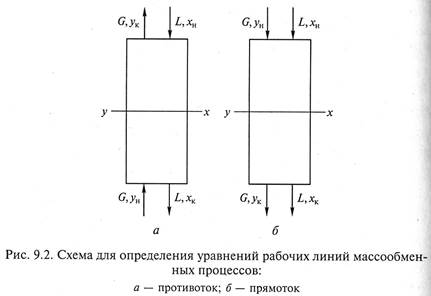
Материальный баланс и уравнение рабочей линии при массопередаче (2 видео)

Материальный баланс

Рассмотрим массообменный процесс между фазами G и L в противоточном аппарате, схема которого представлена на рис. 9.1. Будем считать, что начальные х_н, у_н и конечные х_к, у_к массовые (мольные) концентрации распределяемого вещества в фазах G и L соответствуют его переходу из фазы G в фазу L. В этом случае на некотором малом участке произвольного сечения массоо6менного аппарата концентрация компонента М в фазе L увеличится на величину dх, а в фазе G уменьшится на величину dу (по ходу движения фазы).

Таким образом, переданное количество dМ распределяемого компонента можно записать как по одной, таки по другой распределяющим фазам:

Уравнение (9.2) является дифференциальным уравнением материального баланса массообменного процесса.

Для получения полного (интегрального) уравнения материального баланса проинтегрируем его в пределах изменения рабочих концентраций

Легко убедиться, что уравнение (9.3), так же как и (9.2), не зависит от направления движения взаимодействующих фаз, а характеризует только материальный баланс системы при массопередаче.

Важной характеристикой массоо6менных процессов являются уравнения рабочих линий, которые связывают между собой концентрации распределяемого компонента в распределяющих фазах во время осуществления процесса.

Различают два основных способа взаимодействия распределяющих фаз в процессе массообмена: противоток и прямоток.

1. Противоточная схема проведения процесса массопередачи (рис. 9.2, а).

Используя уравнение материального баланса (9.2), проинтегрируем его для верхней части аппарата в указанных на схеме пределах:

В результате получаем уравнение рабочей линии противоточного процесса массопередачи

которое является уравнением прямой с тангенсом угла наклона L/G. Второе слагаемое является постоянной величиной, Не меняющейся в случае интегрирования уравнения (9.2) в пределах концентраций в нижней части массообменного аппарата.

2. Прямоточная схема осуществления процесса массопередачи (рис. 9.2, б).

Интегрирование уравнения (9.2) произведем также для верхней части массообменного аппарата в указанных на схеме пределах:

В результате получаем уравнение рабочей линии прямоточного процесса массопередачи

Уравнение (9.5) также является уравнением прямой линии, однако угол наклона этой прямой противоположен углу наклона рабочей линии противоточного массообменного процесса, о чем указывает знак « — » перед значением тангенса угла (L/G) наклона прямой.

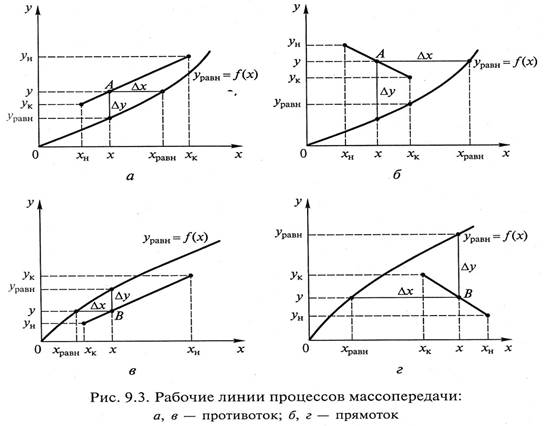
Изображения рабочих линий процесса массопередачи для противотока и прямотока представлены на рис. 9.3.

Движущая сила массоо6менного процесса определяется степенью отклонения системы от равновесия и может быть выражена разностью содержаний целевого компонента в рабочем и равновесном состояниях системы (Δу или Δх). Направление переноса

распределяемого вещества удобно определять на диаграмме у – х по расположению равновесной и рабочей линий.

Если рабочая линия расположена выше линии равновесия (рис. 9.3, а, б), то для любой точки, расположенной на этой линии (точка А), у > у_равн и х х_равн.

При таком процессе распределяемый компонент будет переходить из фазы L в фазу G, причем движущая сила в точке В, выраженная через концентрации соответствующих фаз, может быть записана как Δу = у_равн – y и Δх = х – х_равн.

Скорость массопередачи может быть выражена через количество вещества, переходящего в единицу времени из одной фазы в другую. В этом случае, в соответствии с (В. 3) можно записать основное уравнение массопередачи в дифференциальном

или интегральном (для стационарных процессов) виде

Скорость массопередачи связана с механизмом переноса распределяемого вещества в фазах, между которыми происходит массообмен.

Перенос вещества в фазах может происходить либо путем молекулярной диффузии, либо конвекцией и молекулярной диффузией одновременно (конвективная диффузия).

Массопередача молекулярной диффузией осуществляется в неподвижной среде вследствие движения молекул, атомов и ионов.

Массопередача конвективной диффузией реализуется в движущейся среде. При этом если движение жидкости обусловлено градиентами температуры или концентрацией, то такая конвекция называется свободной, или естественной. Если движение вызвано внешними силами, конвекция является вынужденной.

В случае турбулентного движения жидкости, сопровождающегося массопередачей, в ряде случаев рассматривают турбулентный механизм переноса вещества, при котором оно переносится беспорядочными турбулентными пульсациями потока. Такой механизм называется турбулентной диффузией.

Молекулярная диффузия описывается первым законом Фика, в соответствии с которым количество продиффундировавшего вещества dМ пропорционально градиенту концентрации в направлении диффузии дс/дп, площади массопередачи dF, перпендикулярной направлению диффузионного потока и времени осуществления процесса dτ,

где 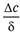— изменение концентрации вещества по толщине слоя δ.

Коэффициент пропорциональности D в уравнениях (9.8) и (9.9) называется коэффициентом молекулярной диффузии и имеет размерность м 2 /с при с, кг/м 3 .

Коэффициент молекулярной диффузии показывает, какая масса вещества диффундирует в единицу времени через единицу поверхности при градиенте концентрации, равном единице. Значение коэффициента молекулярной диффузии зависит от природы и свойств как распределяемого вещества, таки среды, через которую он диффундирует, а также давления и температуры. Причем увеличению его значения способствует повышение температуры и уменьшение давления. Знак минус перед правой частью уравнения (9.8) указывает на то, что молекулярная диффузия протекает в направлении уменьшения концентрации распределяемого компонента.

В ряде случаев по аналогии с первым законом Фика, записывают уравнение, характеризующее массопередачу в результате турбулентной диффузии,

где D_турб – коэффициент турбулентной диффузии, зависящий от гидродинамических условий протекания процесса — скорости потока и масштаба турбулентных пульсаций.

Конвективная диффузия характеризуется тем, что полный поток вещества складывается из конвективного и диффузионного потоков.

Поскольку конвективный перенос вещества осуществляется преимущественно потоками жидкости, его интенсивность учитывается компонентами скорости перемещения массы, диффузионная составляющая – коэффициентом молекулярной диффузии и суммой вторых производных концентраций по соответствующим координатам

Уравнение (9.10) является дифференциальным уравнением конвективной диффузии.

При массоо6мене в неподвижном слое проекции скорости на оси координат W_x = W_y = =W_z= 0, и уравнение (9.10) преобразуется в дифференциальное уравнение молекулярной диффузии (второй закон Фика)

Трудности теоретического описания и расчета процесса массопередачи обусловлены сложностью механизма переноса вещества к границе раздела фаз и от нее, недостаточной изученностью гидродинамических закономерностей турбулентных потоков, особенно вблизи границы раздела фаз.

В связи с этим предложен ряд теоретических моделей, в основу большинства которых положены допущения:

· общее сопротивление процессу массопередачи складывается из сопротивления распределяющих фаз. Сопротивлением поверхности разделав большинстве случаев можно пренебречь;

· на поверхности раздела фазы находятся в равновесии.

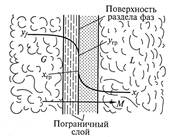
На рис. 9.4 представлена схема массопередачи между система ми жидкость – газ (пар) или жидкость — жидкость. Фазы разделены поверхностью раздела и движутся друг относительно друга с некоторой скоростью.

Процесс массопередачи заключается в переносе распределяемого вещества из фазы G к поверхности раздела фаз (процесс массоотдачи), а затем массоотдачи от поверхности раздела к фазе L.

Процесс массопередачи связан со структурой потока в каждой фазе, которая включает турбулентное ядро потока, где массоперенос осуществляется конвекцией и концентрация компонента практически постоянна. При приближении к поверхности раздела в пограничном слое происходит затухание пульсаций, преобладание механизма молекулярной диффузии, а следовательно, резкое уменьшение концентраций.

Для нахождения скорости перехода вещества из одной фазы к поверхности раздела фаз и далее от нее во вторую фазу используют уравнения массоотдачи, которые для схемы, представленной на рис. 9.4, можно записать как

где у_f — у_гр и х_гр — х_f – движущие силы в процессах массоотдачи в фазах G и L; F – поверхность массопередачи; β_y и β_х – коэффициенты массоотдачи (β, м/с, при размерности единичной движу щей силы – кг/м 3 ).

Коэффициент массоотдачи показывает, какое количество вещества переходит из ядра потока к поверхности раздела (или наоборот) через единицу площади поверхности за единицу времени при движущей силе, равной единице, и зависит в первую очередь от гидродинамических условий.

Если равновесная линия массообменного процесса – прямая с тангенсом угла наклона А_равн, то между коэффициентами массопередачи К_y, К_х из уравнений (9.6) (9.7) и коэффициентами массоотдачи β_y, β_х из уравнений (9.11) (9.12) существует однозначная связь

Коэффициент массопередачи показывает, какое количество вещества переходит из одной фазы в другую за единицу времени через единицу площади поверхности контакта фаз при движущей силе массопередачи, равной единице. Размерность коэффициента массопередачи совпадает с размерностью коэффициента массоотдачи.

Поскольку величины, обратные значениям коэффициентов массопередачи, представляют собой общее сопротивление переносу вещества из фазы в фазу (В.3), то выражения в знаменателях уравнений (9.13) представляют сумму сопротивлении массоотдачи в фазах.

Для расчетов коэффициентов массоотдачи β_х и β_y чаще всего используют уравнения, которые получают на основании теории подобия.

Дата добавления: 2015-08-14 ; просмотров: 3557 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Содержание

Лекция № 11 Процесс массопередачи
Равновесие при массопередаче
Ф + С = К + 2, (1)
Скорость массопередачи
МАТЕРИАЛЬНЫЙ БАЛАНС МАССООБМЕННЫХ ПРОЦЕССОВ
🔥 Видео

Видео:Основы массорепедачи. Первая лекцияСкачать

Лекция № 11 Процесс массопередачи

Массопередача – это сложный процесс, включающий перенос вещества (массы) в пределах одной фазы, перенос через поверхность раздела фаз и его перенос в пределах другой фазы. Как известно, при теплопередаче обменивающиеся теплотой среды в большинстве случаев разделены твердой стенкой, в то время как массопередача происходит обычно через границу раздела соприкасающихся фаз. Эта граница может быть либо подвижной (массопередача в системах газ-жидкость или пар-жидкость, жидкость-жидкость), либо неподвижной (массопередача с твердой фазой).

массоотдача – это перенос вещества из фазы к границе раздела фаз или в обратном направлении, т. е. в пределах только одной фазы.

Виды процессов массопередачи. В промышленности применяются в основном следующие процессы массопередачи:

1. Абсорбция — поглощение газа жидкостью, т. е. процесс разделения, характеризуемый переходом вещества из газовой фазы в жидкую.

2. Экстракция (в системе жидкость-жидкость) — извлечение вещества, растворенного в жидкости, другой жидкостью, практически несмешивающейся или частично смешивающейся с первой. При этом извлекаемый компонент исходного раствора переходит из одной жидкой фазы в другую.

8. Перегонка — разделение гомогенных жидких смесей путем взаимного обмена компонентами между жидкостью и паром, полученным испарением разделяемой жидкой смеси.

4. Адсорбция — поглощение компонента газа, пара или раствора твердым пористым поглотителем, т. е. процесс разделения, характеризуемый переходом вещества из газовой (паровой) или жидкой фазы в твердую.

5. Сушка — удаление влаги из твердых материалов, главным образом путем ее испарения.

6. Кристаллизация — выделение твердой фазы в виде кристаллов из растворов или расплавов.

7. Растворение и экстракция (в системе твердое тело — жидкость).

Процессы массопередачи можно разделить на две группы.

К одной группе относятся процессы (абсорбция, экстракция и др.), в которых участвуют минимально три вещества: одно находится только в одной фазе, другое — только во второй фазе, а третье — переходит из одной фазы в другую и представляет собой распределяемое между фазами вещество.

К другой группе относятся процессы (например, перегонка), в которых вещества, составляющие две фазы, обмениваясь компонентами, сами непосредственно участвуют в массопередаче и уже не могут рассматриваться как инертные носители распределяемого вещества.

Скорость массообменных процессов, как правило, лимитируется молекулярной диффузией. Поэтому процессы массопередачи иногда называют диффузионными процессами.

Равновесие при массопередаче

Правило фаз. Знание равновесия в процессах массопередачи позволяет установить пределы, до которых могут протекать эти процессы. В основе равновесия лежит известное правило фаз:

Видео:Процессы и аппараты. Материальный балансСкачать

Ф + С = К + 2, (1)

где Ф — число фаз; С — число степеней свободы, т. е. число независимых переменных, значения которых можно произвольно изменять без нарушения числа или вида (состава) фаз в системе; К — число компонентов системы.

Правило фаз указывает число параметров, которое можно менять произвольно (в известных пределах) при расчете равновесия в процессах масообмена.

Зависимости между независимыми переменными могут быть изображены в плоских координатах в виде так называемых фазовых диаграмм. В расчетах по массопередаче используют диаграммы зависимости давления от концентрации (при t = const), температуры от концентрации (при Р = const) и диаграммы зависимости между равновесными концентрациями фаз, приведенные ниже.

Фазовое равновесие. Линия равновесия. Рассмотрим в качестве примера процесс массопередачи, в котором аммиак, представляющий собой распределяемый компонент, поглощается из его смеси с воздухом чистой водой, т. е. ввиду отсутствия равновесия переходит из газовой фазы Фу, где его концентрация равна у, в жидкую фазу Фх, имеющую начальную концентрацию х = 0. С началом растворения аммиака в воде начнется переход части его молекул в обратном направлении со скоростью, пропорциональной концентрации аммиака в воде и на границе раздела фаз. С течением времени скорость перехода аммиака в воду будет снижаться, а скорость обратного перехода возрастать, причем такой двусторонний переход будет продолжаться до тех пор, пока скорости переноса в обоих направлениях не станут равны друг другу. При равенстве скоростей установится динамическое равновесие, при котором не будет происходить видимого перехода вещества из фазы в фазу.

При равновесии достигается определенная зависимость между предельными или равновесными концентрациями распределяемого вещества в фазах для данных температуры и давления, при которых осуществляется процесс массопередачи.

В условиях равновесия некоторому значению отвечает строго определенная равновесная концентрация в другой фазе, которую обозначим через . Соответственно концентрация у отвечает равновесная концентрация . В самом общем виде связь между концентрациями распределяемого вещества в фазах при равновесии выражается зависимостью:

или . (2)

Любая из этих зависимостей изображается графически линией равновесия, которая либо является кривой, как показано на рис. 1, либо в частном случае — прямой линией. На рис. 1, а показана равновесная кривая для системы с компонентами-носителями, выражающая зависимость равновесной концентрации, например в газовой фазе, от концентрации жидкой фазы при Р = const и t = const. На рис. 1, б приведен пример равновесной кривой для процесса ректификации, построенной при Р = const. Каждая точка кривой, как показано на рисунке, соответствует разным температурам (t1, t2 и т. д.).

Отношение концентраций фаз при равновесии называется коэффициентом распределения . Для разбавленных растворов линия равновесия близка к прямой, и т является практически величиной постоянной, равной тангенсу угла наклона линии равновесия.

Конкретный вид законов равновесного распределения различен для разных процессов массопередачи. Так, например, в процессе абсорбции при низких концентрациях распределяемого вещества в исходном растворе равновесие описывается законом Генри для идеальных растворов в процессах ректификации — законом Рауля и т. д.

Зная линию равновесия для конкретного процесса и рабочие, т. е. неравновесные, концентрации фаз в соответствующих точках, можно определить направление и движущую силу массопередачи в любой точке аппарата. На основе этих данных может быть рассчитана средняя движущая сила, а по ней — скорость процесса массопередачи.

Материальный баланс. Рабочая линия. Рабочие концентрации распределяемого вещества не равны равновесным, и в действующих аппаратах никогда не достигают равновесных значений.

Зависимость между рабочими концентрациями распределяемого вещества в фазах изображается линией, которая носит название рабочей линии процесса. Вид функции или уравнение рабочей линии в его общем виде, является одинаковым для всех массообменных процессов и получается из их материальных балансов.

Рассмотрим схему массообменного аппарата, работающего в режиме идеального вытеснения при противотоке фаз (рис. 2). Пусть в процессе массопередачи из фазы в фазу, например из газовой фазы в жидкую, переходит только один распределяемый компонент (скажем, аммиак).

Сверху в аппарат поступает Lн кг/с одной фазы (жидкой), содержащей вес. долей распределяемого компонента, а снизу из аппарата удаляется Lк кг/с той же фазы, содержащей вес. долей распределяемого компонента. Снизу в аппарат поступает кг/с другой фазы (газовой) концентрацией и сверху удаляется кг/с этой фазы, имеющей концентрацию вес. долей распределяемого компонента.

Тогда материальный баланс по всему веществу

, (3)

и материальный баланс по распределяемому компоненту

. (4)

Теперь напишем уравнения материального баланса для части аппарата от его нижнего конца до некоторого произвольного сечения, для которого расходы фаз составляют G и L кг/с, а их текущие концентрации равны и соответственно.

Материальный баланс по всему веществу

, (5)

и материальный баланс по распределяемому компоненту

. (6)

Решая это уравнение относительно , получим

. (7)

Уравнение (7) представляет собой уравнение рабочей линии, выражающее связь между рабочими концентрациями распределяемого компонента в фазах для произвольного сечения аппарата.

Расходы фаз постоянны по высоте аппарата, например в процессах ректификации, когда числа молей компонентов, которыми обмениваются фазы, равны. В других случаях, если концентрации фаз мало изменяются по высоте аппарата, то расходы фаз по его высоте можно с достаточной для практических целей точностью считать постоянными, т. е. принять L = const и G = const. При этом Lк = L, Gн = G и уравнение (7) приводится к виду

. (8)

Вводя обозначения и , находим

. (9)

Выражения (8) и (9) являются уравнениями рабочей линии, которыми обычно пользуются при расчетах массообменных процессов.

Таким образом, рабочая линия представляет собой прямую, которая наклонена к горизонту под углом, тангенс которого равен А, и отсекает на оси ординат отрезок, равный В. Рабочая линия для всего аппарата ограничена точками с координатами и (верхний конец аппарата, рис. 3) и и (нижний конец аппарата).

Скорость массопередачи

Скорость массопередачи связана с механизмом переноса распределяемого вещества в фазах между которыми происходит массообмен.

Перенос вещества внутри фазы может происходить только путем молекулярной диффузии либо путем конвекции и молекулярной диффузии одновременно. Посредством одной молекулярной диффузии вещество перемещается, строго говоря, лишь в неподвижной среде. В движущейся среде перенос вещества осуществляется как молекулярной диффузией, так и самой средой в направлении ее движения или отдельными ее частицами в разнообразных направлениях.

В турбулентном потоке перенос молекулярной диффузией преобладает только вблизи границы фазы. При турбулентном течении возникают нерегулярные пульсации скорости, под действием которых, наряду с общим движением потока, происходит перемещение частиц во всех направлениях, в том числе и в поперечном.

Конвективный перенос вещества, осуществляемый под действием турбулентных пульсаций, часто называют турбулентной диффузией.

Молекулярная диффузия. Молекулярной диффузией называется перенос распределяемого вещества, обусловленный беспорядочным тепловым движением молекул, атомов, ионов, коллоидных частиц. Молекулярная диффузия описывается первым законом Ф и к а, согласно которому масса вещества dМ, продиффундировавшего за время dt через элементарную поверхность dF (нормальную к направлению диффузии), пропорциональна градиенту концентрации этого вещества

или . (1)

Из выражения (1) следует, что удельный поток вещества, переносимого молекулярной диффузией через единицу поверхности (F = 1) в. единицу времени (t = 1), или скорость молекулярной диффузии, составляет

. (2)

По своей структуре закон Фика аналогичен закону Фурье, описывающему передачу тепла теплопроводностью, причем аналогом градиента температур является в данном случае градиент концентраций, представляющий собой изменение концентрации диффундирующего вещества на единицу длины нормали между двумя поверхностями постоянных, но различных концентраций.

Коэффициент пропорциональности D в выражении закона Фика называется коэффициентом молекулярной диффузии, или просто коэффициентом диффузии. Знак минус перед правой частью первого закона Фика указывает на то, что молекулярная диффузия всегда протекает в направлении уменьшения концентрации распределяемого компонента.

Согласно уравнению (1), коэффициент диффузии выражается как:

откуда (до сокращения одноименных величин) вытекает физический смысл D. Коэффициент диффузии, показывает, какая масса вещества диффундирует в единицу времени через единицу поверхности при градиенте концентрации, равном единице.

Коэффициент молекулярной диффузии представляет собой физическую константу, характеризующую способность данного вещества проникать вследствие диффузии в неподвижную среду. Величина D таким образом не зависит от гидродинамических условий, в которых протекает процесс.

Турбулентная диффузия. Масса вещества dMт, переносимого в пределах фазы вследствие турбулентной диффузии, может быть принята, по аналогии с молекулярной диффузией, пропорциональной поверхности dF, времени dt и градиенту концентрации и определяется по, уравнению

, (3)

где — коэффициент турбулентной диффузии.

Коэффициент турбулентной диффузии показывает какая масса вещества передается посредством турбулентной диффузии в единицу времени через единицу поверхности при градиенте концентрации, равном единице.

Коэффициент выражается в тех же единицах, что и коэффициент молекулярной диффузии D, т. е. в м2/с. Однако в отличие от D коэффициент турбулентной диффузии не является физической константой; он зависит от гидродинамических условий, определяемых в основном скоростью потока и масштабом турбулентности.

Конвективный перенос. Скорость конвективного, переноса вещества вместе с самой средой в направлении, совпадающем с направлением общего потока, равна

, (4)

где v — скорость потока жидкости, газа или пара; С — коэффициент пропорциональности.

Суммарный перенос вещества вследствие конвективного переноса и молекулярной диффузии, по аналогии с теплообменом, называют конвективным массообменом или конвективной диффузией.

Распределение концентрации при переносе путем конвективной диффузии определяется в самом общем виде дифференциальным уравнением конвективной диффузии.

Дифференциальное уравнение конвективной диффузии. Выделим в потоке данной фазы элементарный параллелепипед с ребрами dx, dy и dz, ориентированными относительно осей координат, как показано на рис. 1. Рассмотрим материальный баланс по распределяемому веществу для параллелепипеда в наиболее общем случае неустановившегося массообмена. Будем считать, что процесс переноса происходит в условиях установившегося движения потока фазы. Распределяемое вещество проходит сквозь грани параллелепипеда как путем конвективного переноса, так и молекулярной диффузии.

Обозначим концентрацию распределяемого вещества в плоскости левей грани параллелепипеда площадью dydz через с и проекции скорости на оси координат для данного элемента (точки) потока — через , и , соответственно.

Тогда масса вещества, поступающего только путем конвективной диффузии через площадь dydz, т. е. в направлении оси х, за время dt составит

. (5)

На противоположной грани параллелепипеда скорость в направлении оси х равна и концентрация распределяемого вещества составляет . Следовательно, за время dt через противоположную грань параллелепипеда выходит путем конвективной диффузии:

. (6)

Разность между массами вещества, прошедшего через противоположные грани параллелепипеда за время dt в направлении оси х, равна

, (7)

где dV = dx dy dz — объем элементарного параллелепипеда. Аналогично в направлении осей у и z:

и . (8)

Таким образом, содержание распределяемого вещества в объеме параллелепипеда изменится за время dt вследствие перемещения вещества только путем конвективной диффузии на величину

или в развернутом виде

. (9)

Согласно уравнению неразрывности потока для установившегося движения фазы

. (10)

Следовательно, предыдущее выражение dMк примет вид

. (11)

Масса распределяемого вещества, поступающего в параллелепипед только путем молекулярной диффузии через грань dy dz за время dt составляет

. (12)

Масса вещества, выходящего за то же время путем молекулярной диффузии через противоположную грань,

. (13)

Разность между массами продиффундировавшего через противоположные грани параллелепипеда вещества в направлении оси х за время dt равна

. (14)

Аналогично в направлении осей у и z:

и . (15)

Масса распределяемого вещества в объеме всего параллелепипеда за время dt изменится при переносе путем молекулярной диффузии на величину

. (16)

В результате изменение массы распределяемого вещества во времени в объеме параллелепипеда

. (17)

Изменение массы распределяемого вещества за счет конвективной и молекулярной диффузии в объеме параллелепипеда по закону сохранения массы должно равняться соответствующему изменению массы этого вещества во времени, т. е.

. (19)

Проводя соответствующие сокращения и перегруппировывая члены этого уравнения, получим

(20)

или в более краткой записи

. (20, а)

Уравнение (20) представляет собой дифференциальное уравнение конвективной диффузии. Оно выражает закон распределения концентрации данного компонента в движущейся стационарно среде при неустановившемся процессе массообмена.

Уравнение (20) по структуре аналогично дифференциальному уравнению конвективного теплообмена (уравнению Фурье-Кирхгофа). Отличие состоит в том, что в уравнение (20) вместо температурного градиента входит градиент концентрации, а вместо коэффициента температуропроводности а — коэффициент молекулярной диффузии D.

Для частного случая установившегося массообмена уравнение (20) принимает вид:

. (21)

При массообмене в неподвижной среде = = = 0, а конвективная составляющая в левой части уравнения (19) равна нулю, и уравнение обращается в дифференциальное уравнение молекулярной диффузии.

. (22)

Уравнение (22) носит название второго закона Фика. В дифференциальном уравнении конвективной диффузии, помимо концентрации, переменной является скорость потока. Поэтому данное уравнение надо рассматривать совместно с дифференциальными уравнениями гидродинамики: уравнениями Навье-Стокса и уравнением неразрывности потока. Однако эта система уравнений не имеет аналитического решения, и для получения расчетных зависимостей по массообмену приходится прибегать к преобразованию дифференциального уравнения конвективной диффузии методами теории подобия.

Ввиду сложности механизма процессов массоотдачи в фазах для практических целей принимают, что скорость массоотдачи пропорциональна движущей силе, равной разности концентраций в ядре и на границе фазы или (в случае обратного направления переноса) разности концентраций на границе и в ядре фазы. Соответственно, если распределяемое вещество переходит из фазы Фу в фазу Фх, то основное уравнение массоотдачи, определяющее количеством М вещества, переносимого в единицу времени в каждой из фаз (к границе фазы или в обратном направлении), выражается следующим образом:

(1)

, (1, а)

входящие в эти уравнения разности концентраций и представляют собой движущую силу процесса массоотдачи соответственно в фазах Фу и Фх, причем и — средние концентрации в основной массе (ядре) каждой из фаз, и — концентрации у границы соответствующей фазы.

Коэффициенты пропорциональности в уравнениях (1) и (1, а) называются коэффициентами массоотдачи. Коэффициенты массоотдачи (в фазе Фх и (в фазе Фу) показывают, какая масса вещества переходит от поверхности раздела фаз в ядро фазы: или в обратном направлении) через единицу поверхности в единицу времени при движущейся силе, равной единице.

Коэффициент массоотдачи является не физической константой, а кинетической характеристикой, зависящей от физических свойств фазы (плотности, вязкости и др.) и гидродинамических условий в ней (ламинарный или турбулентный режим течения), связанных в свою очередь с физическими свойствами фазы, а также с геометрическими факторами, определяемыми конструкцией и размерами массообменного аппарата, Таким образом, величина является функцией многих переменных, что значительно осложняет расчет или опытное определение коэффициентов массоотдачи. Значениями последних учитывается как молекулярный, так и конвективный перенос вещества в фазе.

По своему смыслу коэффициент массоотдачи является аналогом коэффициента теплоотдачи в процессах переноса тепла, а основное уравнение массоотдачи идентично по структуре основному уравнению теплоотдачи.

Коэффициент массоотдачи может быть выражен в различных единицах в зависимости от выбора единиц для массы распределяемого вещества и движущей силы. Если принять, что масса вещества выражена в килограммах, то в общей форме коэффициент массоотдачи выразится следующим образом:

При этом единица измерения р в каждом конкретном случае будет связана с единицами, принятыми для выражения движущей силы (табл. Х-1).

Подобие процессов переноса массы. Наиболее строгий и принципиально возможный путь для определения коэффициентов массоотдачи, заключается в интегрировании уравнения диффузии в движущейся среде (Х,19) совместно с уравнениями движения, т. е. с уравнениями Навье-Стокса и уравнением неразрывности потока при заданных начальных и граничных условиях.

Однако система указанных уравнений практически не имеет общего решения. Поэтому так же, как для гидродинамических и теплообменных процессов, не решая системы основных уравнений, можно методами теории подобия найти связь между переменными, характеризующими процесс переноса в потоке фазы, в виде обобщенного (критериального) уравнения массоотдачи.

Общая функциональная зависимость Nu’ от определяющих критериев и симплексов подобия для неустановившихся процессов массоотдачи может быть выражена как

. (13)

Для установившихся процессов массоотдачи условие равенства критериев Fo’ в сходственных точках подобных потоков отпадает н приведенные выше обобщенные зависимости принимают вид:

. (14)

Расчетная зависимость типа уравнения (13 и 14) называется обобщенным или критериальным уравнением массоотдачи.

Как отмечалось, процесс массопередачи включает процессы массоотдачи в пределах каждой из двух взаимодействующих фаз и, кроме того, процесс переноса распределяемого вещества через поверхность раздела фаз. Сложность расчета процесса связана с тем, что практически невозможно измерить концентрации фаз непосредственно у границы их раздела. Учитывая это, основное уравнение массопередачи, определяющее массу М вещества, переносимого из фазы в фазу в единицу времени (нагрузку аппарата), выражают следующим образом:

, (1)

, (2)

где у*, х* — равновесные концентрации в данной фазе, соответствующие концентрациям распределяемого вещества в основной массе (ядре) другой фазы; Ку, Кх— коэффициенты и массопередачи, выраженные соответственно через концентрации фаз Фу и Фх.

Коэффициент массопередачи (Kу или Кх) показывает, какая масса вещества переходит из фазы в фазу за единицу времени через единицу поверхности контакта фаз при движущей силе массопередачи, равной единице.

По физическому смыслу коэффициенты массопередачи отличаются от коэффициентов массоотдачи, но выражены в одинаковых с ними единицах измерения. Таким образом, коэффициенты массопередачи могут выражаться в м/с, кг/(м2 с); кг/(м2 с мол доли) и в с/м.

Концентрации фаз изменяются при их движении вдоль поверхности раздела, соответственно изменяется движущая сила массопередачи. Поэтому в уравнение массопередачи вводят величину средней движущей силы ( или ). Тогда уравнения (1) и (2) принимают вид:

, (3)

. (4)

С помощью уравнений (3) и (4) обычно находят поверхность контакта фаз F и по ней рассчитывают основные размеры аппарата. Для определения F необходимо предварительно рассчитать коэффициент массопередачи Kу или Кх и среднюю движущую силу. Величина М либо задается при расчете, либо определяется из материального баланса.

Зависимость между коэффициентами массопередачи и массоотдачи. Чтобы установить связь между коэффициентом массопередачи и коэффициентами массоотдачи, обычно принимают, что да границе раздела фаз см. рис. 5) достигается равновесие. Это предположение равносильно допущению о том, что сопротивлением переносу через границу раздела фаз можно пренебречь. Отсюда вытекает, как следствие, положение об аддитивности фазовых сопротивлений, которое является одной из предпосылок для расчета коэффициента массопередачи. Допустим, что распределяемое вещество переходит из фазы Фу в фазу Фх, и движущая сила массопередачи выражается в концентрациях фазы Фу. При установившемся процессе массопередачи количество вещества, переходящее из фазы в фазу, определим по уравнению (1).

Для упрощения рассмотрим случай, когда равновесная зависимость % между концентрациями в фазах линейна, т. е. линия равновесия описывается уравнением у* = m x, где т – тангенс угла наклона линии равновесия. После ряда преобразований получаем

(9)

При выражении коэффициента массопередачи в концентрациях фазы Фх аналогичные рассуждения приводят к зависимости

, (10)

Левые части уравнений (9) и (10) представляют собой общее сопротивление переносу вещества из фазы в фазу, т. е. сопротивление массопередаче, а их правые части — сумму сопротивлений массоотдаче в фазах. Поэтому зависимости (9) и (10) являются уравнениями аддитивности фазовых сопротивлений.

При т = const уравнение (10) можно получить, разделив уравнение (9) на т. Отсюда следует, что величины Kу и Kх связаны зависимостью Kу = Kх/m.

Уравнения аддитивности (9) и (10) выведены для линейной равновесной зависимости, но они остаются в силе и для кривой линии равновесия.

Видео:Лекция 2 МассопередачаСкачать

МАТЕРИАЛЬНЫЙ БАЛАНС МАССООБМЕННЫХ ПРОЦЕССОВ

Основы составления материальных балансов, в том числе и массообменных процессов, были рассмотрены в гл. 1. Материальные балансы конкретных массообменных процессов будут даны ниже в соответствующих главах. В этом разделе будет рассмотрен подход к составлению материальных балансов массообменных процессов с учетом их специфики.

Материальные балансы массообменных процессов зависят от способа их проведения. Различают однократное, непрерывное и ступенчатое взаимодействие фаз.

Однократное взаимодействие характерно для периодических процессов, как правило при малой производительное! и. При этом фазы смешиваются, а после завершения процесса разделяются (например, проведение периодического процесса жидкостной экстракции в аппарате с мешалкой).

Материальный баланс такою процесса в целом и по i-му компоненту имеет вид

где С_н и G_к начальное и конечное количество фазы Ф_у; L_н и L_к –начальной и конечное количество фазы Ф_х; у_in и x_in , у_i_к и x_i_к –начальные и конечные концентрации i-гo компонента в фазах Ф_у и Ф_х соответственно.

Если величины С и L мало изменяются с изменением состава, т. е. G_н ≈ G_к и L_н ≈L_к, то из уравнения (15.8) получаем

. (15.9)

Уравнение (15.9) выражает составы получаемых продуктов разделения в зависимости от относительного расхода фаз L/G и является уравнением рабочей линии.

В массообменных аппаратах непрерывного действия процесс может происходить при непрерывном контакте фаз (например, в абсорбционных аппаратах пленочного типа, представляющих собой, по существу, кожухотрубчатый теплообменник, по внутренним поверхностям трубок которого течет пленка жидкости, а навстречу этой жидкости движется газ). При этом концентрации распределяемого вещества в фазах изменяются монотонно.

В массообменных аппаратах ступенчатого типа (например, в вертикальных аппаратах с горизонтальными перегородками-тарелками) в каждой ступени происходит взаимодействие фаз (см. разд. 16.53), а по выходе из ступени –их разделение. Проведение процесса при непрерывном и ступенчатом взаимодействии фаз существенно зависит от направления относительного движения фаз (прямоток, противоток и др.) и гидродинамической структуры их потоков.

При непрерывном противотоке, наиболее часто используемом в технике (рис. 15-1, а), материальный баланс для произвольного сечения аппарата при бесконечно малом пути выражается следующими соотношениями:

по всему потоку -dG = dL,

Рис. 15-1. К соединению материального баланса при непрерывном контакте фаз в условиях противотока (а) и прямотока (б)

Интегрирование в пределах от начальных значений входящих в это соотношение величин до их значений в произвольном сечении дает

При малом изменении величин G и L по высоте аппарата

Соотношение (15.11) называют уравнением рабочей линии непрерывного противоточного массообменного процесса. Оно выражает связь cocтавов взаимодействующих фаз в произвольном сечении аппарата. При L/G = const рабочая линия прямая. Если L/G ¹ const, то рабочая линия отклоняется от прямой.

При непрерывном прямотоке фазы движутся в одном направлении (рис. 15-1,6). На рис. 15-1,6 показано движение фаз сверху вниз, но в принципе может осуществляться и противоположное совместное их движение -снизу вверх, при котором между фазами идет процесс массопереноса. Как и в случае противотока, уравнения материального баланса имеют вид (для бесконечно малого пути)

для всего потока -dG = -dL,

Итерирование этих уравнений в пределах изменения переменных (от начальных на входе в аппарат до конечных на выходе из него) дает уравнение материальных балансов по потокам и любому i-му компоненту:

Для получения более общего уравнения, описывающего изменение состава фаз но высоте массообменного аппарата, проинтегрируем исходные уравнения в пределах от начальных (или конечных) значений величин, входящих в эти уравнения, до их значений в произвольном сечении (см. рис 15-1,6). Тогда получим

Уравнения (15.12) показывают, что по высоте массообменного аппарата происходит лишь перераспределение i-го компонента между фазами, общее же количество вещества и любого i-го компонента по высоте аппарата остаются неизменными. При условии, что величины G и L мало изменяются по высоте аппарата, из уравнений (15.12) получим выражение

которое является уравнением рабочей линии непрерывного прямоточного массообменного процесса. Сравнение этого уравнения — с уравнением (15.11) показывает, что они аналогичны по форме, отличаясь лишь знаком перед величиной (L/G)(x_i — x_i_н).

Отметим, что уравнения (15,11) и (15.13) получены для условий отсутствия продольного перемешивания в массообменном аппарате, т. е. для модели идеального вытеснения.

МОЛЕКУЛЯРНАЯ ДИФФУЗИЯ

Ранее отмечалось (см. гл. 3), что в потоке идут два вида массопереноса—молекулярный и конвективный.

Молекулярная диффузия описывается первым законом Фика:

Для всей поверхности F диффузии первый закон Фика выразится как

где D — коэффициент молекулярной диффузии; F-поверхность, нормальная к направлению диффузии; дс/дп-градиент концентраций вещества на единицу длины пути п диффундирующего вещества; знак минус связан с уменьшением градиента концентраций дс/дп по длине пути диффузии.

Коэффициент молекулярной диффузии D зависит от природы диффундирующего вещества. Поэтому он не связан с динамикой процесса и характеризует способность вещества проникать в какую-либо среду. Найдем его размерность из выражения (15.14a):

откуда следует, что коэффициент молекулярной диффузии D показывает, какое количество вещества диффундирует в единицу времени через единицу поверхности при градиенте концентрации, равном единице. Коэффициент молекулярной диффузии D является аналогом коэффициента температуропроводности а.

Значения D находят по справочникам или рассчитывают. Например,

, (15.15)

, (15.16)

где Т -абсолютная температура, К; Р давление, Па; V_A и V_Bмолярные объемы взаимодействующих веществ, см 3 /моль; М_А и М_В молярные массы, кг/кмоль; m-вязкость жидкости, в которой происходит диффузия, Па · с.

Таким образом, коэффициент диффузии зависит от температуры (увеличивается с повышением температуры) и для газов -от давления (с увеличением давления D_r снижается).

Для газовой среды D_r ≈ 1 см 2 /с, для конденсированной (жидкой) среды D_ж ≈ 1 см 2 /сут, откуда следует, что молекулярная диффузия в жидкостях, а тем более в твердых телах -процесс очень медленный.

Строго говоря, движущей силой процесса молекулярной диффузии является градиент химического потенциала вещества (под химическим потенциалом, как известно, понимают частные производные характеристических функций по числам молей компонентов N_i при всех других постоянных параметрах состояния, например дH/дN_i = m_i = дU/дN_i=дG/дN_i ,где Н-энтальпия, V внутренняя энергия, G-энергия Гиббса. Но для случая переноса одного компонента m_i=f(с_i), где с_i-концентрация i-го компонента в смеси. Тогда в качестве движущей силы можно использовать градиент концентраций, что намного упрощает расчеты. При невысоких концентрациях компонентов в реальных системах также можно использовать градиент концентраций в качестве движущей силы. Для достаточно концентрированных реальных систем при использовании в качестве движущей силы градиента концентраций следует учитывать влияние на величину коэффициента молекулярной диффузии состава системы (разделяемой смеси).