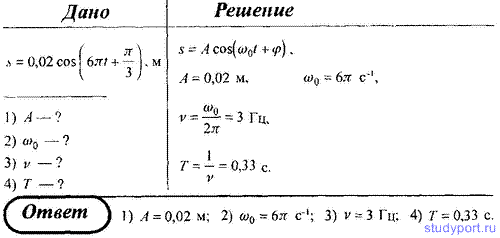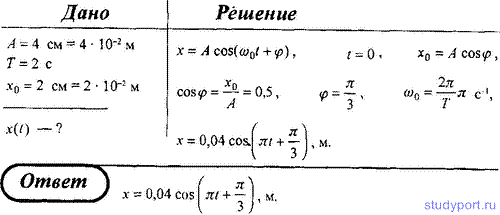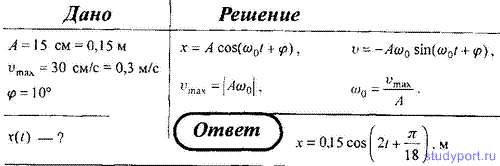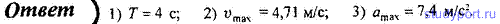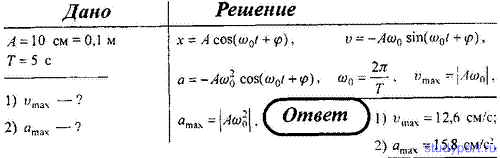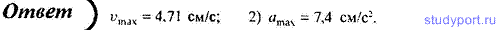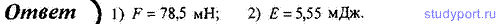Материальная точка совершает гармонические колебания согласно уравнению x 2sin

Видео:Уравнения и графики механических гармонических колебаний. Практ. часть - решение задачи. 11 класс.Скачать

Механические и электромагнитные колебания

4. Колебания и волны

1. Гармонические колебания величины s описываются уравнением s = 0,02 cos (6πt + π/3), м. Определите: 1) амплитуду колебаний; 2) циклическую частоту; 3) частоту колебаний; 4) период колебаний.

2. Запишите уравнение гармонического колебательного движения точки, совершающей колебания с амплитудой A = 8 см, если за t = 1 мин совершается n = 120 колебаний и начальная фаза колебаний равна 45°.

3. Материальная точка совершает гармонические колебания с амплитудой A = 4 см и периодом T = 2 с. Напишите уравнение движения точки, если ее движение начинается из положения x₀ = 2 см.

4. Точка совершает гармонические колебания с периодом T = 6 с и начальной фазой, равной нулю. Определите, за какое время, считая от начала движения, точка сместится от положения равновесия на половину амплитуды.

5. Напишите уравнение гармонического колебания точки, если его амплитуда A = 15 см, максимальная скорость колеблющейся точки v_max = 30 см/с, начальная фаза φ = 10°.

6. Точка совершает гармонические колебания по закону x = 3 cos (πt/2 + π/8), м. Определите: 1) период T колебаний: 2) максимальную скорость V_max точки; 3) максимальное ускорение a_max точки.

7. Точка совершает гармонические колебания с амплитудой A = 10 см и периодом T = 5 с. Определите для точки: 1) максимальную скорость; 2) максимальное ускорение.

8. Скорость материальной точки, совершающей гармонические колебания, задается уравнением v(t) = -6 sin 2 πt, м/с. Запишите зависимость смещения этой точки от времени.

9. Материальная точка совершает колебания согласно уравнению x = A sin ωt. В какой-то момент времени смещение точки x₁ = 15 см. При возрастании фазы колебания в два раза смещение x₂ оказалось равным 24 см. Определите амплитуду A колебания.

10. Материальная точка совершает гармонические колебания согласно уравнению x = 0,02 cos (πt + π/2), м. Определите: 1) амплитуду колебаний; 2) период колебаний; 3) начальную фазу колебаний; 4) максимальную скорость точки; 5) максимальное ускорение точки; 6) через сколько времени после начала отсчета точка будет проходить через положение равновесия.

11. Определите максимальные значения скорости и ускорения точки, совершающей гармонические колебания с амплитудой A = 3 см и периодом T = 4 с.

12. Материальная точка, совершающая гармонические колебания с частотой ν = 1 Гц, в момент времени t = 0 проходит положение, определяемое координатой х₀ = 5 см, со скоростью v₀ = -15 см/с. Определите амплитуду колебаний.

13. Тело массой m = 10 г совершает гармонические колебания по закону х = 0,1 cos(4πt + π/4), м. Определите максимальные значения: 1) возвращающей силы; 2) кинетической энергии.

14. Материальная точка массой m = 50 г совершает гармонические колебания согласно уравнению x = 0,1 cos 3πt/2, м. Определите: 1) возвращающую силу F для момента времени t = 0,5 с; 2) полную энергию Е точки.

15. Материальная точка массой m = 20 г совершает гармонические колебания по закону x = 0,1 cos(4πt + π/4), м. Определите полную энергию Е этой точки.

16. Полная энергия E гармонически колеблющейся точки равна 10 мкДж, а максимальная сила F_max, действующая на точку, равна -0,5 мН. Напишите уравнение движения этой точки, если период T колебаний равен 4 с, а начальная фаза φ = π/6.

17. Определите отношение кинетической энергии T точки, совершающей гармонические колебания, к ее потенциальной энергии П, если известна фаза колебания.

18. Определите полную энергию материальной точки массой m, колеблющейся по закону x = A cos(ω₀t + φ).

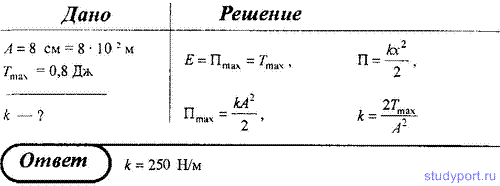
19. Груз, подвешенный к спиральной пружине, колеблется по вертикали с амплитудой A = 8 см. Определите жесткость k пружины, если известно, что максимальная кинетическая энергия T_max груза составляет 0,8 Дж.

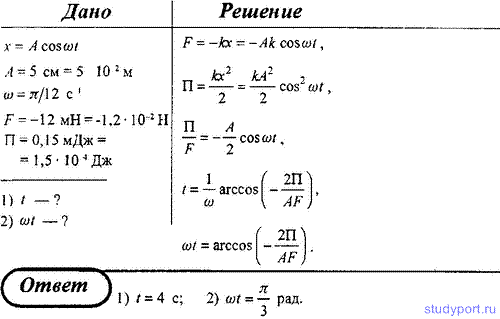
20. Материальная точка колеблется согласно уравнению х = A cos ωt, где A = 5 см и ω = π/12 с -1 . Когда возвращающая сила F в первый раз достигает значения -12 мН, потенциальная энергия П точки оказывается равной 0,15 мДж. Определите: 1) этот момент времени t; 2) соответствующую этому моменту фазу ωt.

Ошибка в тексте? Выдели её мышкой и нажми

Остались рефераты, курсовые, презентации? Поделись с нами — загрузи их здесь!

Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Материальная точка совершает гармонические колебания по закону x = 2sin(П 4 t + П 2), где х — в см?

Физика | 10 — 11 классы

Материальная точка совершает гармонические колебания по закону x = 2sin(П 4 t + П 2), где х — в см.

А t — в секундах.

Определить амплитуду колебаний ; начальную фазу ; период колебания.

Т период Т = 2П / w = 2 * 3, 14 / ( 3.

Видео:Материальная точка совершает гармонические колебанияСкачать

Через сколько времени от начала движения точка, совершающая гармонические колебания по косинусоидальному закону, сместится на половину амплитуды?

Через сколько времени от начала движения точка, совершающая гармонические колебания по косинусоидальному закону, сместится на половину амплитуды?

Период колебаний равен 6 с, начальная фаза равна 0.

Видео:Физика 9 класс. §25 Гармонические колебанияСкачать

Решите пожалуйста?

Материальная точка совершает гармонические колебания по закону : x = 0, 2 sin(4πt — π / 4).

Найти амплитуду, период колебаний, начальную фазу колебаний и смещение точки в начальный момент времени.

Видео:Гармонические колебания | Физика 9 класс #25 | ИнфоурокСкачать

Определите смещение от положения равновесия материальной точки, совершающей косинусоидальные гармонические колебания по истечении 0, 5 с от начала отсчета?

Определите смещение от положения равновесия материальной точки, совершающей косинусоидальные гармонические колебания по истечении 0, 5 с от начала отсчета.

Начальная фаза колебаний π / 6 рад.

, период 6 с, амплитуда колебаний 6 см.

Видео:Физика 9 класс (Урок№11 - Гармонические колебания. Затухающие колебания. Резонанс.)Скачать

Материальная точка совершает гармонические колебания по закону синуса с начальной фазой a = П / 2, частотой v = 2 Гц и амплитудой А = 3 см?

Материальная точка совершает гармонические колебания по закону синуса с начальной фазой a = П / 2, частотой v = 2 Гц и амплитудой А = 3 см.

Запишите уравнение колебаний точки.

Видео:Урок 327. Гармонические колебанияСкачать

Гармонические колебания совершают по закону x = 0, 15cos пt?

Гармонические колебания совершают по закону x = 0, 15cos пt.

Определите амплитуду и период колебаний.

Видео:Выполнялка 53.Гармонические колебания.Скачать

Материальная точка совершает гармонические колебания по закону x = 6 sin(30Пt + П / 3) см где выражено в сантиметрах, t — в секундах?

Материальная точка совершает гармонические колебания по закону x = 6 sin(30Пt + П / 3) см где выражено в сантиметрах, t — в секундах.

Определите амплитуду колебаний, начальную фазу, период.

Видео:Урок 329. Задачи на гармонические колебания - 1Скачать

Уравнение гармонического колебания : 0, 15cos(06Pit Pi / 3)?

Уравнение гармонического колебания : 0, 15cos(06Pit Pi / 3).

Определите амплитуду, начальную фазу и период колебаний.

Видео:КОЛЕБАНИЯ физика 9 класс решение задачСкачать

Период гармонических колебаний материальной точки равен 2, 4 с, амплитуда 5 см, начальная фаза равна нулю?

Период гармонических колебаний материальной точки равен 2, 4 с, амплитуда 5 см, начальная фаза равна нулю.

Определите смещение колеблющейся точки через 0, 6 с после начала колебаний.

Видео:Тема 2. Решение задач по теме «Гармонические колебания»Скачать

Материальная точка совершает гармонические колебания по закону x = 20sin(п / 4t + п / 4) Оперделите период колебаний, амплитуду колебаний и начаоьную ?

Материальная точка совершает гармонические колебания по закону x = 20sin(п / 4t + п / 4) Оперделите период колебаний, амплитуду колебаний и начаоьную .

Видео:Физика 10 класс. Гармонические колебания. Решение задачСкачать

Период гармонических колебаний материальной точки, происходящих по закону синуса, равен 2, 4 с, амплитуда — 5 см, начальная фаза колебаний — нулю?

Период гармонических колебаний материальной точки, происходящих по закону синуса, равен 2, 4 с, амплитуда — 5 см, начальная фаза колебаний — нулю.

Напишите уравнение этих колебаний, а также определите смещение материальной точки через 0, 3 с после начала колебаний.

На этой странице сайта размещен вопрос Материальная точка совершает гармонические колебания по закону x = 2sin(П 4 t + П 2), где х — в см? из категории Физика с правильным ответом на него. Уровень сложности вопроса соответствует знаниям учеников 10 — 11 классов. Здесь же находятся ответы по заданному поиску, которые вы найдете с помощью автоматической системы. Одновременно с ответом на ваш вопрос показаны другие, похожие варианты по заданной теме. На этой странице можно обсудить все варианты ответов с другими пользователями сайта и получить от них наиболее полную подсказку.

Видео:МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ период колебаний частота колебанийСкачать

Материальная точка совершает гармонические колебания по закону

Видео:Гармонические колебания | Физика 11 класс #8 | ИнфоурокСкачать

Условие задачи:

Материальная точка совершает гармонические колебания по закону (x = 2sin left( right)) (м). Определить период колебаний.

Задача №9.1.15 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Видео:Гармонические колебанияСкачать

Решение задачи:

Если материальная точка совершает гармонические колебания, то уравнение этих колебаний в общем случае можно представить в виде:

[x = Asin left( <+ omega t> right)]

В этой формуле (A) – амплитуда колебаний, (omega) – циклическая частота колебаний, (varphi_0) – начальная фаза колебаний.

Поэтому из сравнения легко понять, что циклическая частота колебаний (omega) в нашем случае равна (0,25pi) рад/с.

Циклическая частота колебаний (omega) и период колебаний (T) связаны по формуле:

Видео:МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫСкачать

Ответ: 8 с.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

📸 Видео

10 класс, 19 урок, График гармонического колебанияСкачать

Урок 335. Анализ графика гармонических колебанийСкачать

Тема 1. Колебательное движение. Гармонические колебания. Уравнение гармонических колебанийСкачать

Урок 343. Затухающие колебания (часть 1)Скачать