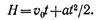Материальная точка массы m движется согласно уравнениям (3 видео)

Содержание

Определение сил по заданному движению
Примеры решения задач
Материальная точка массы m движется согласно уравнениям
📽️ Видео

Видео:ЕГЭ Задание 7. Материальная точка движется по законуСкачать

Определение сил по заданному движению

ДИНАМИКА ТОЧКИ

Определение сил по заданному движению

13.1.1Точка массой m=4 кгдвижется по горизонтальной прямой с ускорениемa=0,3t. Определить модуль силы, действующей на точку в направлении ее движения в момент времени t=3c. (3.6) Решение:Зная массу и ее ускорение, можно определить действующую на точку силу, в момент времени t=3c , ускорение будет

Материальная точка массы m движется согласно уравнениям

тогда

13.1.2Ускорение движения точки массой m=27кгпо прямой задано графиком функции a=а(t). Определить модуль равнодействующей сил, приложенных к точке в момент времени t=5c. (4,05) Решение:Из графика видно что при t=5c , ускорение а=0,15м/с 2 , тогда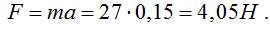

13.1.3 Деталь массой m=0,5кг скользит вниз по лотку. Под каким углом к горизонтальной плоскости должен располагаться лоток, для того чтобы деталь двигалась с ускорением а=2 м/с 2 ? Угол выразить в градусах. (11,8) Решение:Деталь движется под силой тяжести G=mg, сила под которой она движется по

лотку с некоторым углом а,

13.1.4Точка массой m=14кгдвижется по горизонтальной оси Ох с ускорениема_х.=lnt Определить модуль силы, действующей на точку в направлении движения в момент времени t=5c. (22,5) Решение:

13.1.5Трактор, двигаясь с ускорением а=1м/с 2 по горизонтальному участку пути, перемещает нагруженные сани массой 600кг. Определить силу тяги на крюке, если коэффициент трения скольжения саней f=0,04. (835) Решение:Необходимая сила тяги на крюке для перемещения саней с заданным ускорением 1м/с 2 :

13.1.6Тело массой m=50 кг, подвешенное на тросе, поднимается вертикально с ускорением а=0,5м/с 2 . Определить силу натяжения троса.(516) Решение:

13.1.7 Скорость движения точки m=24кг по прямой задана графиком функцииv=v(t). Определить модуль равнодействующей сил, действующих на точку. (36) Решение: из графика функции v=v(t) видно, что точка движется равноускоренно с ускорением а=1,5м/с, тогда равнодействующая сил

13.1.8 Материальная точка массой m=12кгдвижется по прямой со скоростьюv=е 0,1t . Определить модуль равнодействующей сил, действующих на точку в момент времени t=50c.(178) Решение:

13.1.9 Определить модуль равнодействующей сил, действующих на материльную точку массой m=3кг в момент времени t=6c, если она движется по оси Ох согласно уравнению х=0,04t 3 . (4,32) Решение:Ускорение точки найдем из уравнения движения (вторая производная по времени):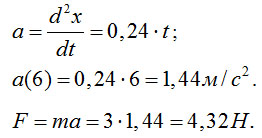

13.1.10 Материальная точка массой 1,4кг движется прямолинейно по законух=6t 2 +6t+3 . Определить модуль равнодействующей сил, приложенных к точке.(16,8) Решение:

Определение сил по заданному движению

Видео:Материальная точка движется прямолинейно по закону x(t) В какой момент времени ее скорость = 2 м/с?Скачать

Примеры решения задач

Пример 1. Свободная материальная точка, масса которой5 кг, движется согласно уравнению S = 0,48t 2 +0,2t. Определить величину движущей силы.

Решение

1. Ускорение точки: a = v’ = S»; v = S’ = 0,96t + 0,2; a = v’ = 0,96 м/с 2 .

2. Действующая сила согласно основному закону динамики F = ma; F = 5 * 0,96 = 4,8 Н.

Пример 2. Тело массой т = 2 кг движется по гладкой горизонтальной поверхности согласно уравнению S = 2t 3 (S — в метрах, (t — в секундах). Определить силу Р в конце второй секунды после начала движения.

Решение

Тело движется по прямой. Следовательно, и сила, действующая на точку, направлена по этой же прямой. Силы, действующие на тело, показаны на рис. 1.57 (тg — сила тяжести тела, N — реакция поверхности, Р — искомая сила).

Определим ускорение тела в конце второй секунды.

Продифференцировав дважды уравнение движения, получим

Ускорение тела в конце второй секунды

Пример 3. К двум материальным точкам массой m₁ = 2 кг и m₂ = 5 кг приложены одинаковые силы. Сравнить величины ускорений.

Решение

Согласно третьей аксиоме динамики ускорения обратно пропорциональны массам:

Пример 4. На материальную точку действует система сил (рис. 13.5). Определить числовое значение ускорения, полученного материальной точкой m = 7 кг. Остальные данные представлены на чертеже.

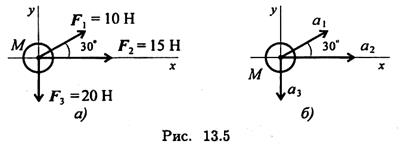
Решение

Й вариант.

1. Определяем суммарную силу, действующую на точку:

2. Определяем ускорение, сообщенное точке:

Й вариант.

Определяем ускорения от каждой из сил системы (рис. 13.5, б):

а₁ = 10/7 = 1,43 м/с 2 , а₂ = 15/7 = 2,14 м/с 2 ; а₃ = 20/7 = 2,86 м/с 2 .

2. Определяем суммарное ускорение:

Пример 4. Материальная точка, сила тяжести которой G = 100 Н, движется по прямолинейной гладкой поверхности (рис. 1.58) с ускорением а = 1,5 м/с 2 . Определить силу Р, вызывающую движение, пренебрегая силами сопротивления.

Решение

Задано движение материальной точки, требуется определить движущую силу (прямая задача динамики). На материальную точку действуют три силы: сила тяжести G, реакция гладкой горизонтальной плоскости N и движущая сила Р.

Силы G и N уравновешены, следовательно, основное уравнение динамики в этом случае имеет вид:

Подставляя числовые значения, получаем

Пример 5. Под действием силы тяжести тело М падает с высоты H = 1500 м, испытывая сопротивление воздуха. Полагая силу сопротивления постоянной и равной половине силы тяжести, найти ускорение тела а и скорость V через 5с после начала движения, если начальная скорость V₀ = 0 (рис. 1.59).

Решение

В данном случае силы заданы, требуется определить кинематические характеристики движения: ускорение, скорость (обратная задача динамики). По основному уравнению получим

Рассматриваемое тело движется равномерно-ускоренно, а = const = 4,9 м/с 2 .

Скорость точки при равномерно-ускоренном движении определяется по формуле

В рассматриваемом примере v₀ = 0, следовательно, v = at.

В конце пятой секунды после начала движения скорость точки

Определим время падения тела.

При равномерно-ускоренном движении

Поскольку v₀ = 0, получаем

Итак, через 24,7 с тело упадет на землю.

Пример 6. В шахте опускается равномерно-ускоренно бадья, сила тяжести которой Q = 280 кН. В первые 10 с она проходит путь S = 35 м. Найти натяжение каната, на котором висит бадья (рис. 1.60).

Решение

На бадью действует сила тяжести Q и натяжение каната Т. Следовательно,

Ускорение а определяем из уравнения

Подставляя числовые значения в формулу, получаем

Контрольные вопросы и задания

1. Что называют массой тела? Назовите единицу измерения массы в системе СИ.

2. Что является мерой инертности тела?

3. Запишите основной закон динамики в векторной и дифференциальной форме.

4. На материальную точку действует постоянная сила. Как движется точка?

5. Какое ускорение получит точка, если на нее действует сила, равная удвоенной силе тяжести?

6. После столкновения двух материальных точек с массами m₁ = 6 кг и m₂ = 24 кг первая точка получила ускорение 1,6 м/с 2 . Чему равно ускорение, полученное второй точкой?

7. В чем заключается принцип независимости действия сил?

8. Перечислите законы трения скольжения.

9. Перечислите факторы, влияющие на величину коэффициента трения скольжения.

10. Тело движется по наклонной плоскости вверх (рис. 13.6). Масса тела 10 кг, коэффициент трения 0,2. Определите возникающую силу трения.

Видео:ЕГЭ по математике. Профильный уровень. Задание 7. Закон движения. ПроизводнаяСкачать

Материальная точка массы m движется согласно уравнениям

материальная точка массой

Материальная точка массой m = 0,1 г колеблется согласно уравнению х = Asinωt, где А = 5 см; ω = 20 с. Определить максимальные значения возвращающей силы F_макс и кинетической энергии T_макс точки.

Определите полную энергию материальной точки массой m, колеблющейся по закону x = А cos(ω₀t + φ).

Материальная точка, масса которой m = 4 г, колеблется с амплитудой X₀ = 4 см и частотой ν = 0,5 Гц. Какова скорость точки в положении, где смещение Х = 2 см?

Материальная точка массой m = 1 кг, двигаясь равномерно, описывает четверть окружности радиусом r = 1,2 м в течение времени t = 2 с. Найти изменение Δр импульса точки.

Колебания материальной точки массой m = 0,1 г происходят согласно уравнению х = Acosωt, где A = 5 см; ω = 20 с –1 . Определить максимальные значения возвращающей силы F_max и кинетической энергии Т_max.

Материальная точка массой т = 1 кг движется по прямой с постоянным ускорением а = 5 м/с 2 . Определить импульс равнодействующей приложенных к точке сил за промежуток времени τ = t₂ – t₁, где t₂ = 4 с, t₁ = 2 с.

Материальная точка массой т = 0,5 кг движется согласно векторному уравнению r = 2 sin πti + 3 cos пtj. Определить проекцию количества движения точки на ось Ох в момент времени t = 0,5 с.

Определить проекцию на ось Оу главного вектора количества движения системы двух материальных точек, массы которых т₁ = 4 кг, m₂ = 2 кг, в момент времени, когда их скорости v₁ = 2 м/с, v₂ = 1 м/с.

Найти закон прямолинейного движения материальной точки массы m, если известно, что работа силы, действующей в направлении движения и зависящей от пути, пропорциональна времени, протекшему с момента начала движения. Коэффициент пропорциональности равен k.

Материальная точка массой m = 0,5 кг совершает движение согласно уравнениям: x = 2t 2 +1; y = t 2 –1. Определить величину и направление силы, действующей на точку, в момент t = 1 с.

Уравнение колебаний МТ массой m = 10 г имеет вид х = 5sin(π/5t + π/4) см. Найти максимальную силу F_max, действующую на точку, и ее полную энергию W.

Материальная точка массой 0,1 г колеблется согласно уравнению х = A sin ωt, где А = 10 см, ω = 25 рад/с. Определить максимальные значения возвращающей силы и кинетической энергии точки.

Две материальные точки массами m расположены симметрично относительно оси O₁O₁‘, расположенной в плоскости чертежа. Как изменится момент инерции этих точек при повороте оси в плоскости чертежа на угол α = 45° из положения O₁O₁‘ в положение O₂O₂‘.

Уравнение колебаний материальной точки массой 0,1 г: х = А sin ωt, где ω = 20 с –1 ; А = 5 см. Определить максимальные значения возвращающей силы и кинетической энергии.

Материальная точка массой m движется в плоскости ху по закону х = R sin(ωt), y = R cos(ωt), где R и ω — положительные постоянные. Определить модуль и направление силы, действующей на точку.